大规模数据的随机森林算法
2020-06-18聂佩芸
李 扬,祁 乐,聂佩芸
(1.中国人民大学 a.应用统计科学研究中心,b.统计学院,c.统计咨询研究中心,北京 100872;2.腾讯公司 国际业务部,广东 深圳 518057)
一、引言
随着信息技术的高速发展,人们生产、收集数据的能力大大提升,越来越多的数据呈现出样本海量化、高维化的趋势。譬如,阿里巴巴集团旗下的淘宝平台仅日交易数据就多达数10TB,Facebook公司每月产生的日志数据业已超过10PB[1],又如Kaggle平台举办的数据挖掘竞赛中向参赛者提供的许多规模庞大的数据集等。大规模数据的广泛应用使传统的统计分析面临计算效率的挑战[2]。以2017年Kaggle举办的建模竞赛中音乐流媒体服务商KKBOX向参赛者提供的日志数据为例,该竞赛要求参赛者通过对日志数据合理建模,以准确预测用户在订阅到期后是否会流失。一方面,每个用户在音乐软件中通过实时点击会产生多种多样的信息,如点击的音乐入口、读取的音乐内容、在软件中停留的时间等,一个小时之内产生的日志记录可达成百上千条。特别地,音乐软件的受众较广,用户往往数以亿计,因此日志数据中包含的样本数量非常庞大,海量化的数据不仅对计算机存储空间等硬件设备提出了新挑战,也将带来较高的计算成本,进一步制约大数据处理技术的时效性;另一方面,从用户、产品以及两者的交互角度出发,日志数据中会存在大量与用户偏好相关的特征变量。同时,为更加准确地了解用户偏好,对于隐藏在用户背后无法被探知的信息,如天气,心情、环境等因素,需要人为探索、构造一些特征来刻画,最终数据的特征维数会大大增加。然而在高维情况下,一些经典的分类方法如Fisher判别分析等常常会失效,且计算效率同样面临严峻的挑战[3]。因此,针对这种样本量大、特征维数高的大规模数据,如何实现高效分析是研究者亟待解决的问题。
目前,许多学者针对算法耗时长、计算效率低的问题提出了相应解决方案。针对样本量较大的情况,Bickel、Kleiner等在自助法(Bootstrap方法)基础上分别又提出了m-n自助法、Bootstrap of Little Bag方法(BLB)[4-5]。这两种方法通过不同方式对数据进行抽样,降低了数据量级,从而在样本量过高时实现了计算效率的提升。但是上述方法会在一定程度上降低数据的变异性,且BLB方法在应用过程中需要同时优化两个参数,即样本子集的数量以及每个样本子集上重复抽样的次数,利用枚举法确定参数也会大大限制该方法在计算时间上的优势。因此,Sengupta等人在此基础上将在每个样本子集上重复抽样的次数固定为1,提出了Subsample Double Bootstrap(SDB)方法,即在BLB方法的基础上以牺牲数据一些变异性为代价,进一步提高计算速度[6]。然而,不论是BLB方法还是SDB方法,它们的出发点均只考虑了数据量大的情境,对特征维度较高时如何实现高效分析并没有进行讨论,因此并不能完全解决大规模数据的计算挑战。同时,还有一类正则化方法比如通过添加惩罚项LASSO、SCAD等,或者在超高维的情况下事先利用边际回归筛选重要变量,在筛选变量的基础上添加惩罚项实现降维,以降低计算复杂度、提高计算的可行性。然而,这类方法也仅仅解决了特征维度方面的计算问题;特别地,当变量间具有较强的相关性时,不宜利用边际回归筛选变量,所以,在这种情况下利用该方法提升计算效率也不具合理性。除此之外,还有一种解决问题的常见思路是将复杂任务分解为多个子任务,通过并行计算节约运行时间[7]。比如钟龙申、Luo等分别将并行化计算方式应用在随机森林算法以及带有正则化约束的支持向量机算法中以提高运算效率[8-9];又如Fang和Ma针对大规模数据提出了一种自助加罚法(Bootstrap Penalization),该方法同时从特征维度、样本维度出发,通过将计算复杂的加罚任务拆分成多个低计算量的子任务,使其在多台计算机上并行计算,最终通过加权的方式将不同的子任务的结果合并进行决策,显著的减少了运算时间,提高了计算的可行性[10]。但是,这种方法主要针对加罚估计的问题进行讨论,且实现过程中涉及多个调节参数的选取,不同的调节参数可能会对估计结果产生不同程度的影响。随机森林是由Breiman在Bagging 集成学习理论基础上提出的一种通过多棵分类回归树进行组合预测的统计算法。目前针对随机森林算法的优化研究大多还只集中在提升算法精度上,比如如何进行特征选择、参数优化以及处理样本不平衡等问题。吴琼等、曹正凤、汪桂金分别利用NCL(Neighborhood Cleaning Rule)技术、聚类算法、SMOTE算法等思想对随机森林算法进行改进以解决样本不平衡带来的算法性能下降的挑战[11-13]。Paul等在随机森林算法中借鉴了强化学习的思想,提出了增强随机森林(Reinforced Random Forest)[14],马景义等结合Adaboost 算法和随机森林算法的优点提出了拟自适应随机森林,这两种新算法在提高分类的准确性上均取得了不错的效果[15]。Gall 等对随机森林的投票过程进行了优化改进[16]。特别地,针对面向高维数据的随机森林算法存在的不足,汪桂金还提出了基于智能算法的随机森林特征选择和参数优化,并通过搭建分布式计算平台 Hadoop 对并行化随机森林算法展开研究[13]。然而,这类并行运算的方法主要利用了外在计算平台的优势降低计算成本。
因此结合前人研究,为了在尽量保证算法有效性的前提下同时解决大规模数据样本量大、特征维度高带来的计算问题,本文利用“分治”思想提出了一种分析框架,并以随机森林算法为例内嵌其中提出大规模随机森林算法(BLOCK-SDB-RF),以探索机器学习算法在大规模高维实际数据分析中的作用。
二、方法
(一)基础算法
随机森林是一种以决策树为基学习器的集成算法,通过样本维度的Bootstrap重抽样与特征维度的随机抽样制造出更多的随机性,以实现减少预测方差的目的。在决策树的建立过程中,通过测度输出变量的异质性指标找到决策树节点的最佳分组变量与最佳分割点。令X表示自变量,Y表示因变量,对于分类问题,一般采用Gini指数或信息熵测度输出变量的异质性,见式(1)、式(2),其中pk表示样本属于第k类的概率,k=1,2,…,|Y|,|Y|表示数据集D中包含的类别数。
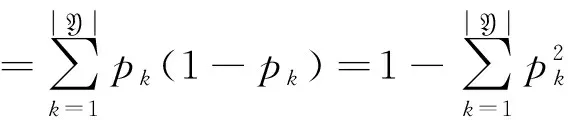
(1)
(2)
对于回归问题,方差常常被用来测量输出变量的异质性,见式(3)。
(3)
异质性指标越高,意味着数据的杂乱程度越深。因此,为了使决策树更好的实现分类(回归),往往通过最大化输出变量的异质性指标减少量构建决策树。以分类问题中的Gini指数为例,需要优化的具体模型如式(4)。

(4)
其中,t表示决策树节点,Gini(t)和N表示分组前输出变量的Gini指数和样本量,Nr、Gini(tr)、Nl、Gini(tl)分别代表分组后右子树、左子树的Gini指数及样本量。最佳分组变量与最佳分割点应是使ΔGini(t)最大的变量与分割点。
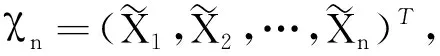
(二)大规模随机森林算法
BLOCK-SDB-RF利用“分治”思想处理大规模数据,算法设计主要解决由样本量大、特征维数高导致的计算效率低的问题。通过对样本维度与特征维度同时进行处理,BLOCK-SDB-RF方法可以有效减少计算时间,提高计算效率。
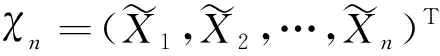
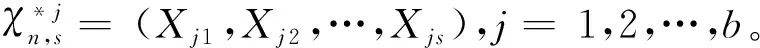
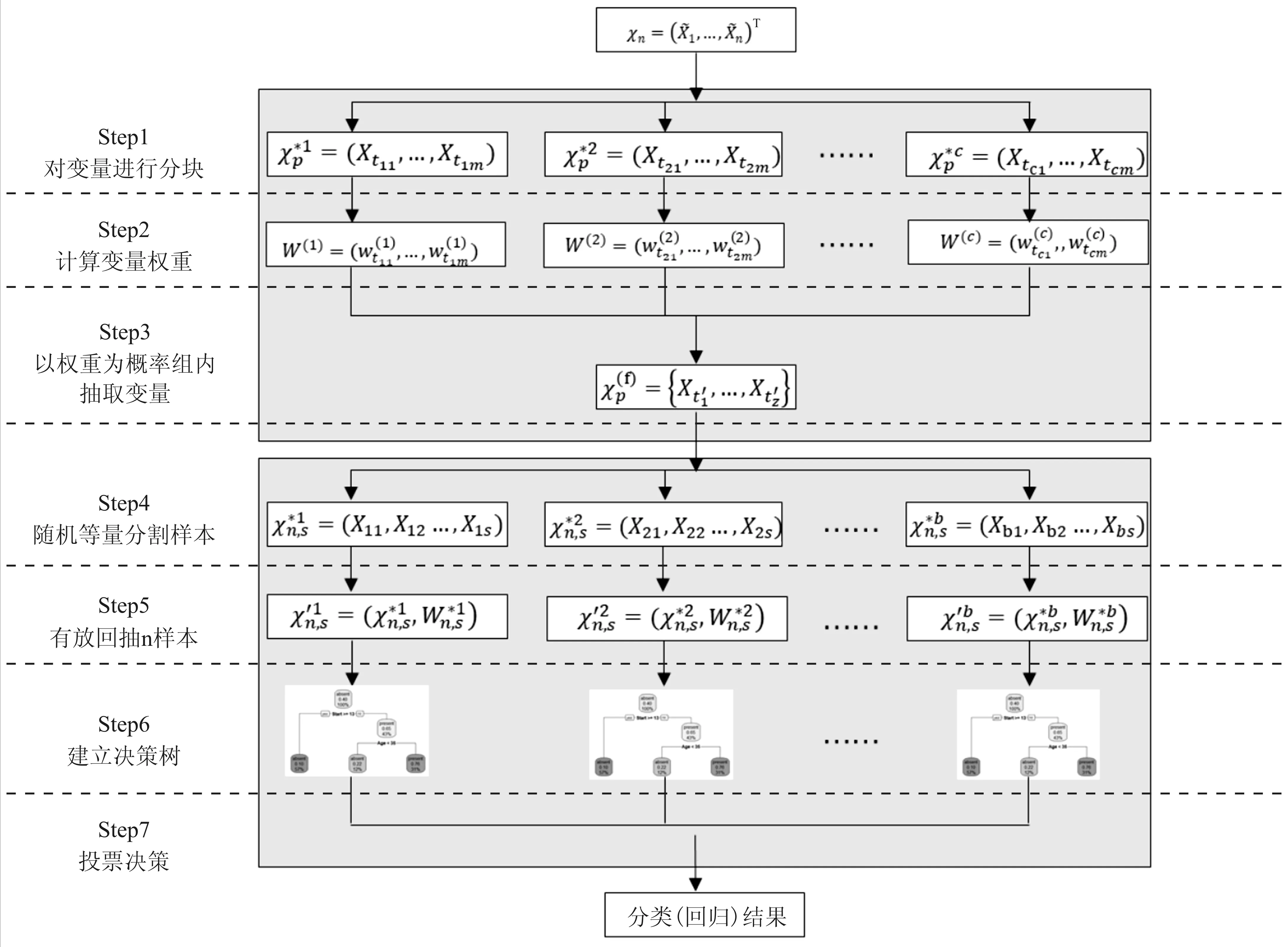
显然地,BLOCK-SDB-RF方法对特征维度的分组降维解决了随机森林算法在特征维数较高时带来的过拟合及信息损失的问题。同时,以特征的重要性为权重在每组特征中随机抽取一部分(所有组总计抽取z维特征)作为最终建模的变量,这样既保证了所有特征变量均有进入到模型的可能,又增大了重要特征被抽中的可能性,从而减少算法的信息损失。另一方面,通过对样本维度的随机分块,减少了构建每棵决策树所需样本中不重复样本的数量,有利于降低每棵决策树的运行时间。即便最终子集的样本量恢复到与原数据集相同,但考虑到子集中不重复的样本数至多只有s个,计算时只需通过对样本加权即可用较短的时间得出结果,并不会因此增加运算成本。算法的整体思路与流程见图1。
(三)时间复杂度及数据覆盖率分析
1.时间复杂度分析
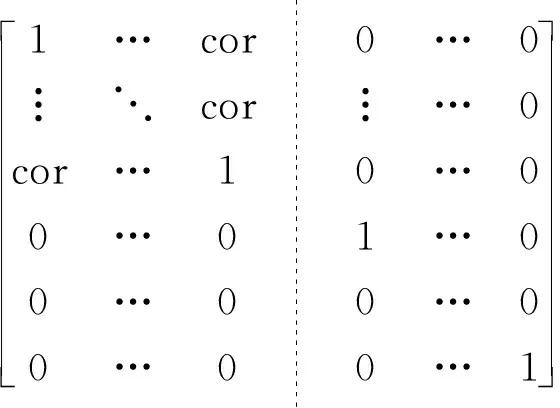
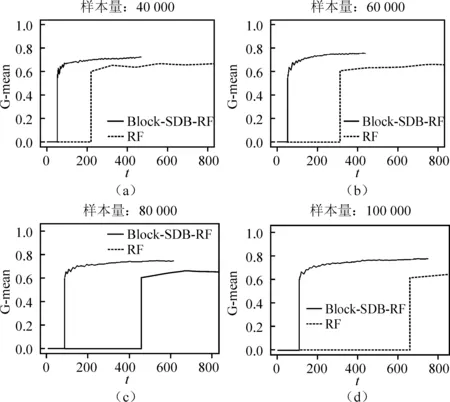
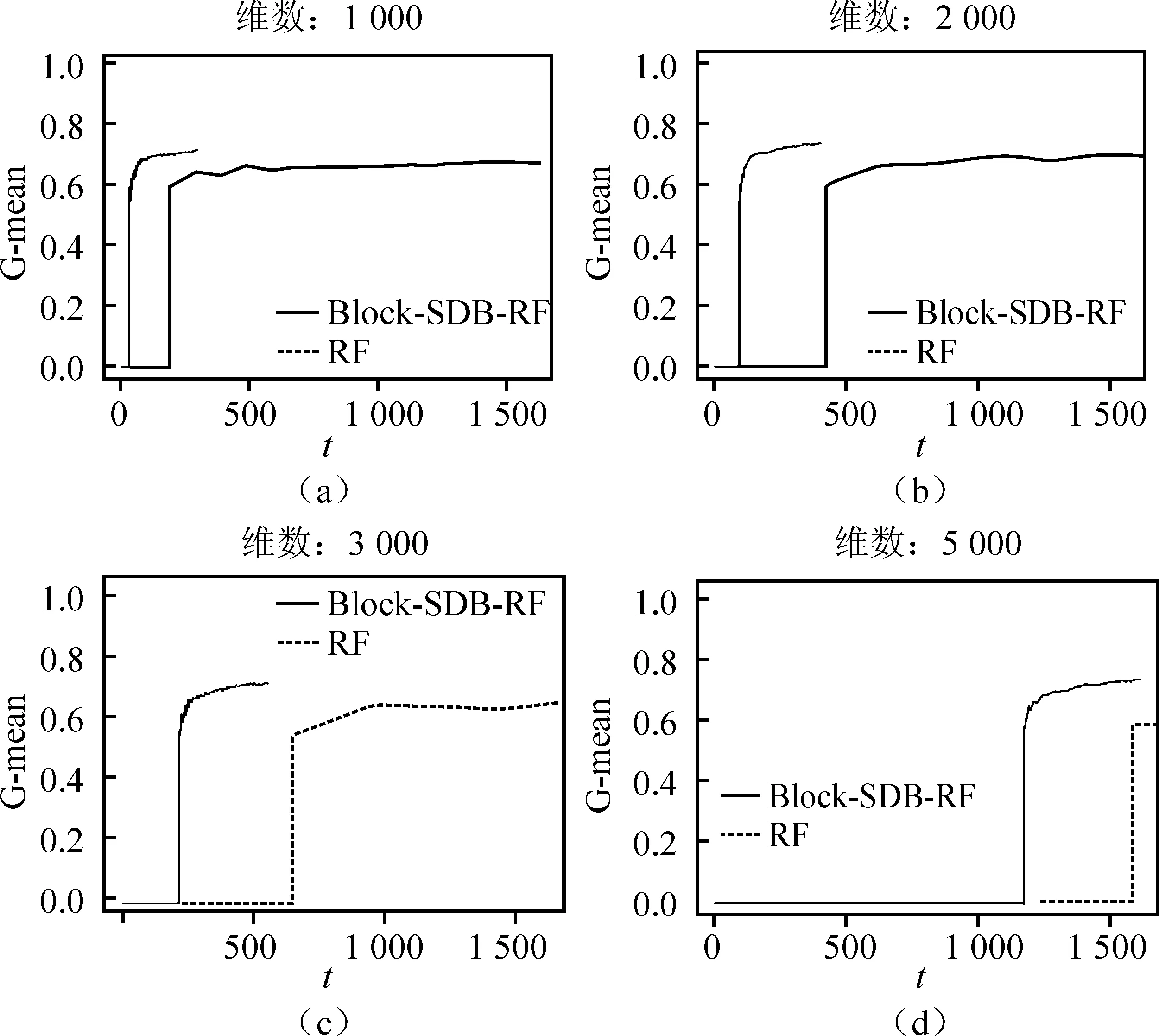
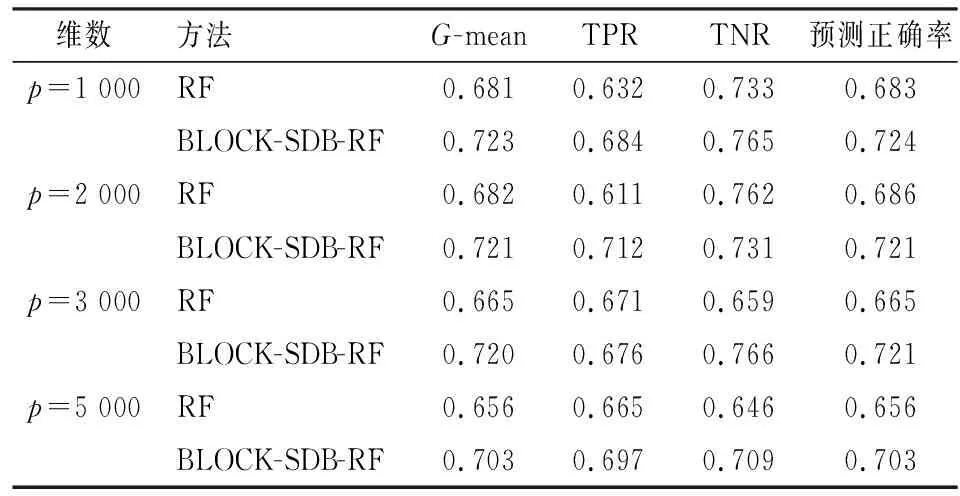
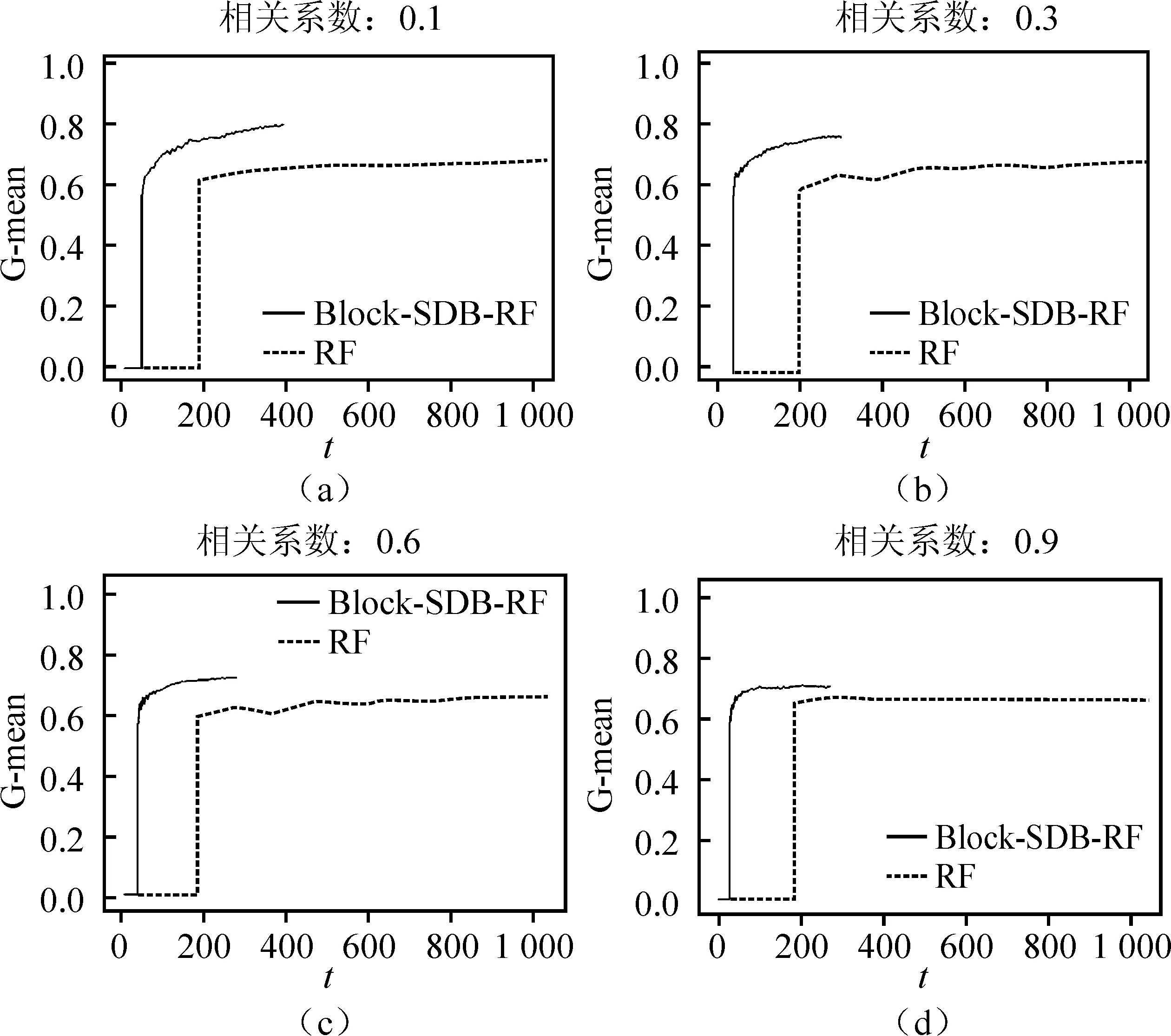
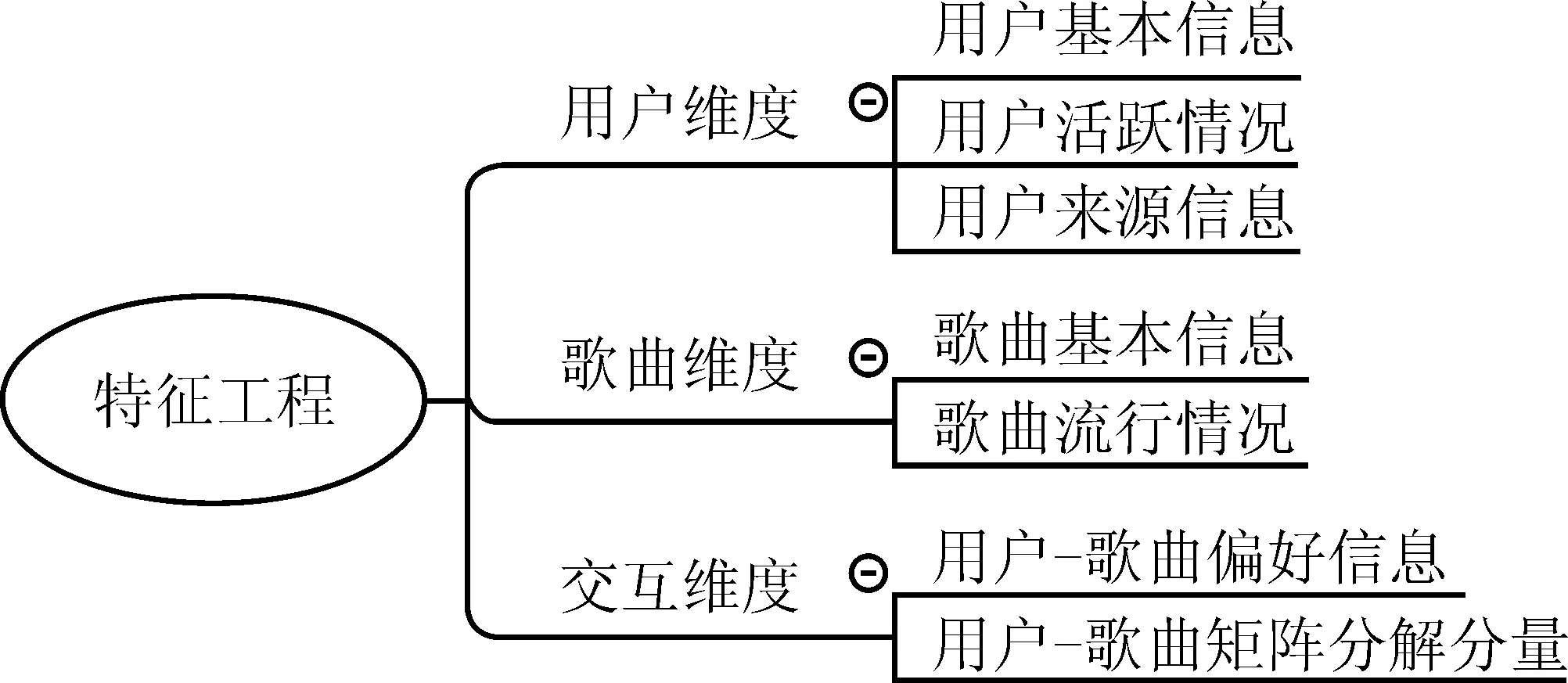
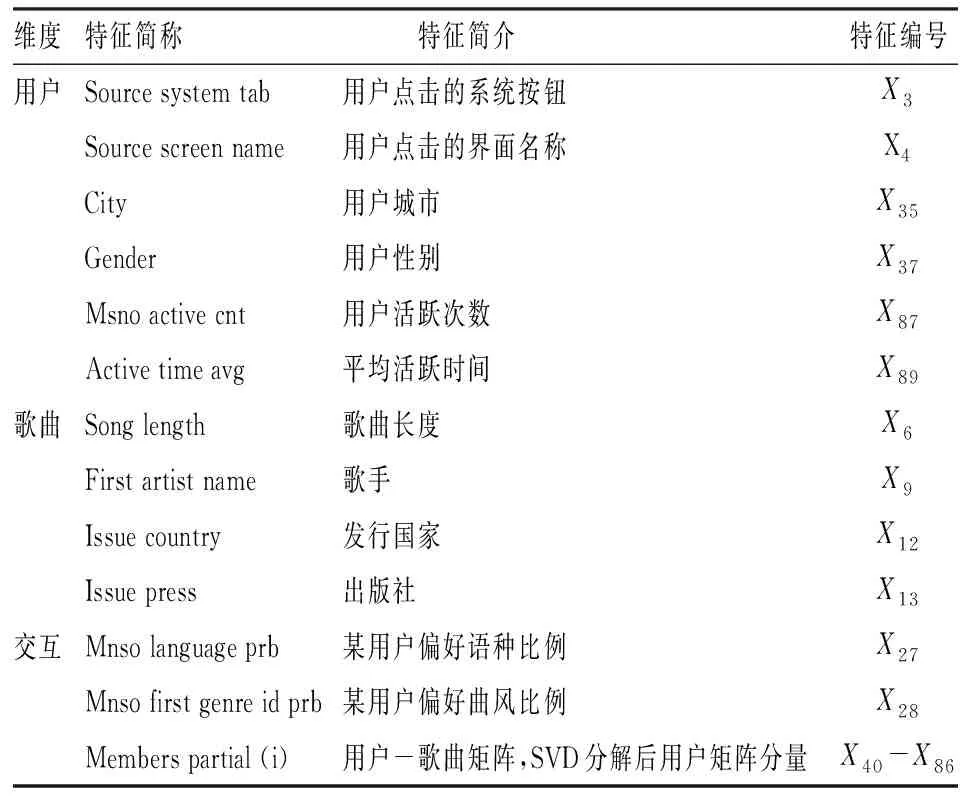
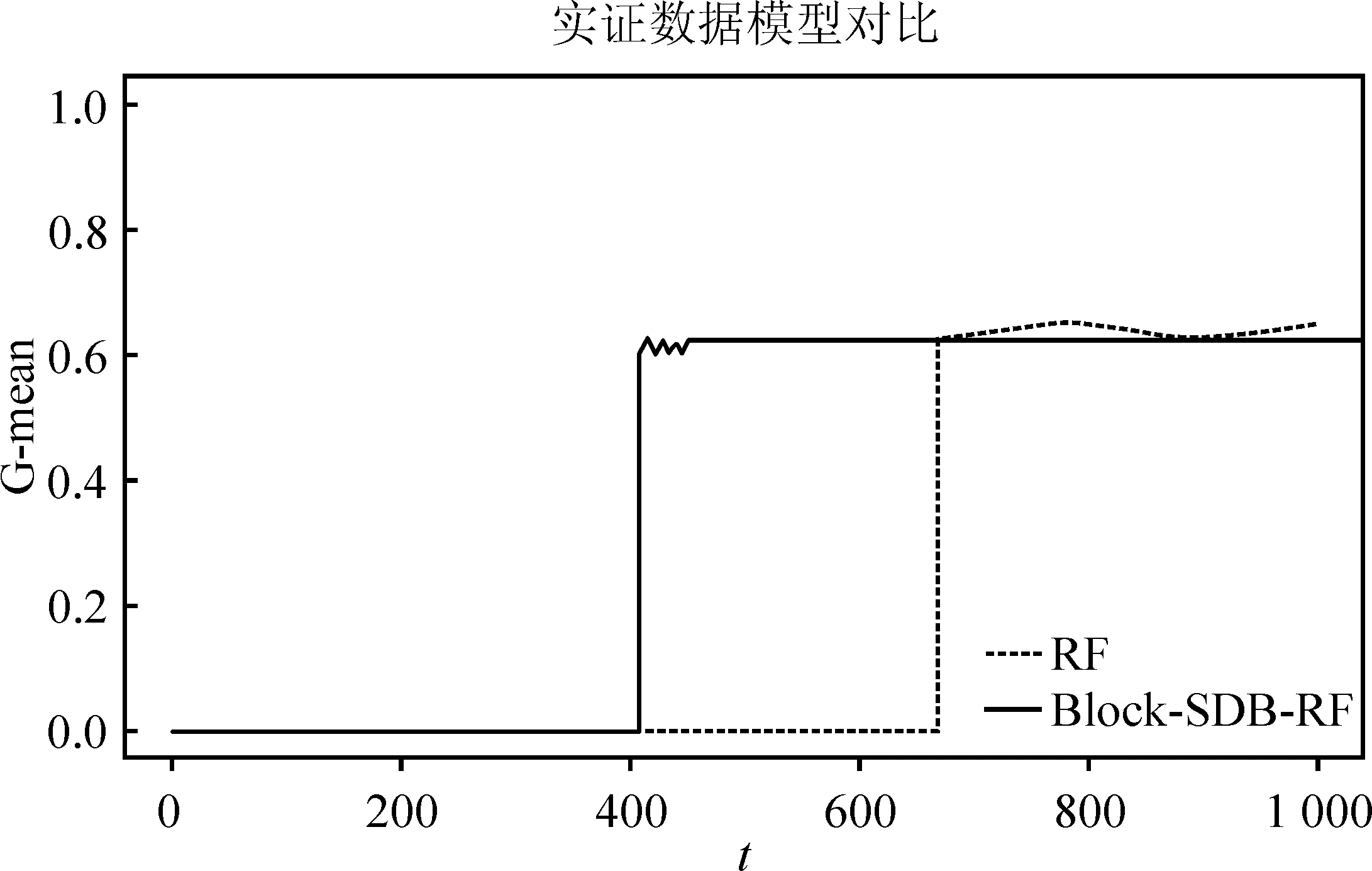
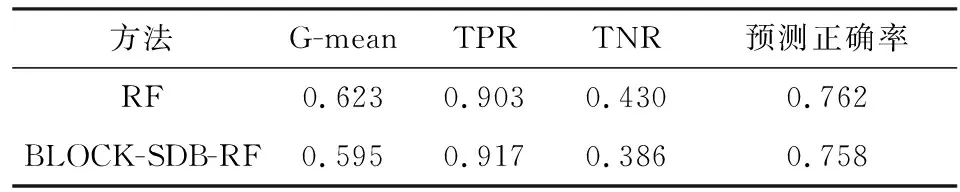
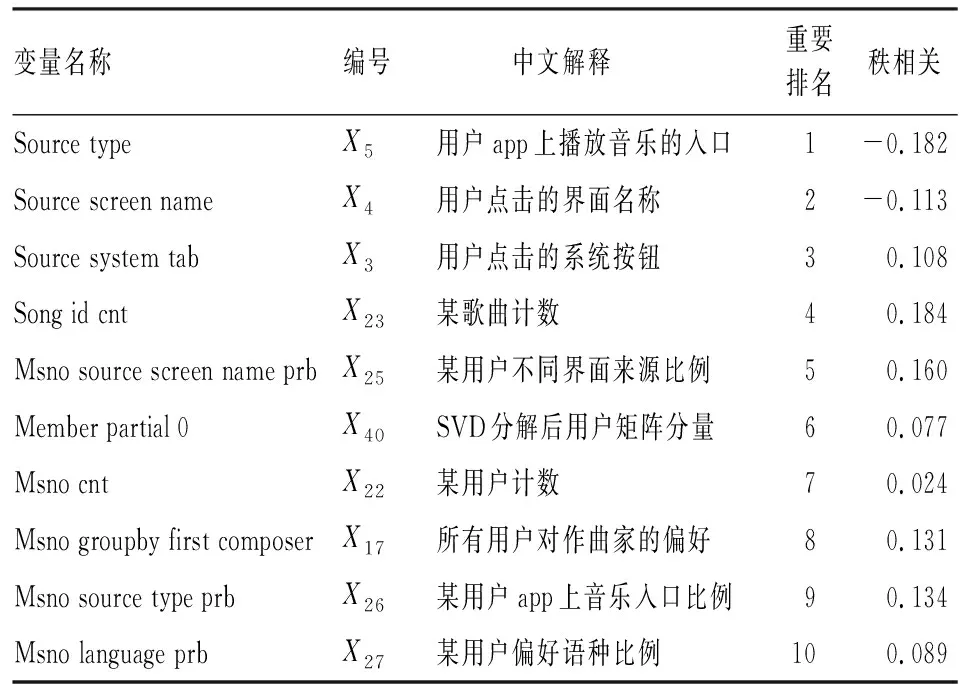
算法的时间复杂度需要从样本维度和特征维度两方面考虑。从样本维度看,随机森林算法需对原数据集进行R次Bootstrap抽样,所得的每一个子样本集至多包含n个不同的样本,其样本维度的时间复杂度可以表示为(R+1)×t(n);BLOCK-SDB-RF在b个大小为s的子样本集上分别进行一次有放回抽样,所得样本集最多只包含s个不同的样本,相应样本维度的时间复杂度可记为2b×t(s)。从特征维度看,由于随机森林算法对每一个Bootstrap子样本集都从p维特征中抽取比例为1/2的变量建立一棵决策树,因此特征维度的时间复杂度为(R+1)×t(p);同理,考虑到BLOCK-SDB-RF方法通过分组降维将变量维数降低至z,相应特征维度的时间复杂度为2b×t(z)。因此,BLOCK-SDB-RF的总时间复杂度可记为2b×t(sz),随机森林算法的总时间复杂度记为(R+1)×t(np)。在单机运算的前提下,运算成本的对比情况会受到Bootstrap抽样次数R和子样本集数量b的大小的影响。然而Sengupta等提到,在BLB方法中推荐R取值为100,b根据情况推荐取值在2到10之间,因此一般来讲,BLOCK-SDB-RF方法的时间成本更加低廉。在并行计算的前提下,由于s、z相较n、p更小,显然有t(sz) 输入: 输出:分类结果或回归结果。 过程: 1.将χp=(X1,X2,…,Xp)随机划分为c组: 2.从χn中随机抽取比例q的样本构成样本集合χn,q 3.fori1 toc end 6.forj1 to b end 7.结合b棵决策树的分类结果或回归结果进行综合决策 图1 BLOCK-SDB-RF算法结构图 2.数据覆盖率分析 为了在数据覆盖率方面对BLOCK-SDB-RF方法、RF方法实现更加公平比较,研究者在给定相同的时间成本下,分别计算两种方法对数据的覆盖情况。同时,为了便于比较,提出了两个假设条件: 条件1:不失一般性,假定RF方法Bootstrap抽样次数R=1; 条件2:假定时间复杂度t(np)、t(sz)满足条件t(np)≥bt(sz)。 提出条件1的目的是为了限制时间成本,在给定RF方法Bootstrap抽样次数R=1的前提下,相应的时间成本为(R+1)×t(np)。条件2的提出给定了时间复杂度t(np)、t(sz)的大小关系,该条件的成立意味着在一个样本量为n、特征维数为p的数据集上建立一棵决策树的耗时大于或等于在一个样本量为s、特征维数为z的数据集上建立决策树耗时的b倍。这也是为了实现数据覆盖率的对比而提出的条件,事实上,两个时间复杂度的大小未必总是符合线性关系的条件。从数据覆盖率看,当满足以上两个条件时,在相同的时间成本下BLOCK-SDB-RF方法能覆盖到更多的数据。事实上,在随机森林算法的实现过程中,每一次利用Bootstrap抽取子样本集时,由于单个样本的入样概率为1/n,重复抽取n次后,大约有(1-1/n)n的样本在整个算法中不会参与训练模型。当n趋于无穷大时,约有1/e的样本从未被抽中,即在随机森林算法的一次Bootstrap抽样中,样本覆盖率约为1-1/e。同样地,在BLOCK-SDB-RF中每一个子集的Bootstrap抽样大约有s/n×(1-1/s)n的样本在整个算法中不会参与训练模型。当数据集的样本量特别高时,可以认为BLOCK-SDB-RF方法的一个子集样本Bootstrap抽样覆盖率是s/n×[1-(1/e)b]。当Bootstrap抽样次数R=1时,RF方法的数据覆盖率约为1-1/e,在相同的时间成本下利用BLOCK-SDB-RF方法进行计算时,由于t(np)≥bt(sz),可以覆盖到b×{s/n×[1-(1/e)b]}的数据,即此时BLOCK-SDB-RF方法的数据覆盖率为1-(1/e)b,显然高于随机森林算法。 为证明BLOCK-SDB-RF方法在不同类型实际数据中具有良好的应用效果,本文以随机森林方法(以下记为RF)为参照,分别设置了不同样本量、不同特征维数场景下的模拟分析,同时考虑到变量间往往并不完全相互独立,增加第三种模拟场景以探究在变量间相关性不同的情况下两种方法的效果对比。 在模拟数据中,Xn×p从均值为零向量的p元正态分布中生成,该多元正态分布的协方差矩阵为分块对角矩阵,如式(5)所示。协方差矩阵由虚线划分为4部分,其中设定第一部分大小为10×10的子矩阵中元素非零,即除前10个变量间具有系数为cor的相关关系以外,其他变量间均不具有相关性。Yn×1由线性回归模型Y=Xβ+ε生成,然后通过Sigmoid变换将其转化为0-1变量。其中,随机干扰项ε服从标准正态分布N(0,1),自变量系数β设为{a,…,a,-a,…,-a,0,…,0},a与-a的数量均为10,且a从正态分布N(3,0.5)中产生。 1…cor0…0︙⋱cor︙…0cor…10…00…01…00…00…00…00…1 (5) 研究采用以下指标以度量BLOCK-SDB-RF方法的应用效果。其中TPR为召回率,表示所有正类中,有多少被预测成正类(正类预测正确)。TNR表示所有反类中,有多少被预测成反类(反类预测正确)。预测正确率Accuracy表示所有样本中分类正确的比例,指标G-mean的含义比TPR、TNR更加综合,具体定义为: 与预测正确率Accuracy的区别在于当正负样本存在不平衡时G-mean的参考价值较大。四类指标均为越高越好。 在第一个模拟场景中,设定特征维数p=1 000,变量间相关系数cor=0.5。分别考虑数据样本量为40 000、60 000、80 000、100 000的情况下,BLOCK-SDB-RF方法和RF方法的应用效果,结果见图2。图2中 (a)、(b)、(c)、(d)的横轴名称为t,表示计算耗费的时间,纵轴为指标G-mean,用以衡量预测结果的准确率,该指标越大意味着预测结果越准确;图2中实线表示BLOCK-SDB-RF方法,虚线表示RF方法。为便于对两种方法进行对比,借鉴Sengupta等的思路考虑在相同的计算时间内哪种方法能以更快的速度达到合理准确的结果,此处结合模拟场景将时间限定为800秒[6]。 由图2(a)可见,BLOCK-SDB-RF方法的G-mean指标在30秒附近急剧增加并很快达到稳定状态,较短时间内完成了计算;而RF方法的G-mean指标在近200秒附近才有相似的变化,800秒内并没有完成计算。可见与RF方法相比,BLOCK-SDB-RF方法的计算以更快的速度达到收敛,图2(b)、(c)、(d)的情况类似。同时,与图2(b)、(c)、(d)对比发现,随着数据的样本量不断增加,BLOCK-SDB-RF与RF两种方法的G-mean指标达到一定程度的耗时差距越来越大,表明BLOCK-SDB-RF方法在数据的样本量越大时计算速度的优势越突出。 图2 不同数据量下的方法对比图 另一方面,为了进一步比较两种算法的准确性,给出四种指标G-mean、TPR、TNR,预测正确率的对比情况,见表1。其中,TPR、TNR分别表示正、负样本中预测正确的比例,G-mean、预测正确率度量了总体的预测准确率,四类指标均为越高越好。由表1见,在不同的样本数量下,BLOCK-SDB-RF方法的表现基本上优于RF方法。 表1 算法准确性对比 第二种场景下,设定数据的样本量n=40 000,变量间相关系数cor=0.5。比较RF和BLOCK-SDB-RF两种方法在特征维数分别为1 000,2 000,3 000,5 000时的表现,结果见图3。考虑到变量维数增加,为了更清晰的展示结果,将时间限定为1 600秒。 图3 不同特征维数下的方法对比图 与第一种模拟场景相同,图中横轴为t,表示计算耗费的时间,纵轴为指标G-mean,实线表示BLOCK-SDB-RF方法,虚线表示RF方法。结果显示,在特征维数为1 000时,BLOCK-SDB-RF方法的G-mean指标50秒左右达到了稳定状态,仅在500秒内就完成了计算;而RF方法在200秒附近G-mean 指标才有显著的增长,具体参见图3(a)。同时由图3(b)、(c)、(d)可见,不论特征维数高低,BLOCK-SDB-RF方法总是可以在更短时间完成计算,并以比RF方法更快的计算速度使结果的G-mean指标达到稳定。同时,随着特征维数的不断增加,两种方法所需的计算时间也越长。特别地,BLOCK-SDB-RF达到一定预测精度的耗时短于RF方法的程度越来越大,表明BLOCK-SDB-RF在特征维数不断增长时计算速度的优势越来越明显。 表2 算法准确性对比 同样的,从分类准确性的角度来看,不论特征维度高低,BLOCK-SDB-RF方法的表现也基本上优于RF方法。特别的,随着特征维度的增加,RF方法的G-mean和预测正确率指标有逐步下降的趋势,而BLOCK-SDB-RF方法的准确率相对更加稳定。 在实际中,变量间往往并不是完全相互独立的,为探究变量间的不同相关性对两种方法计算效果的影响,本节设定数据的样本量n=40 000,p=1 000,比较在变量间相关性分别为0.1,0.3,0.6,0.9四种情况下,BLOCK-SDB-RF和RF方法在计算速度方面的差异。同样地,为便于对两种方法进行对比,此处结合模拟场景将时间限定为1 000秒,结果见图4。 图4 不同变量间相关性的方法对比图 表3 算法准确性对比 图4(a)显示,在变量间相关系数为0.1时,BLOCK-SDB-RF方法的G-mean指标在40秒左右快速增长,200秒左右就完成了运算;而RF方法在限定的1 000秒内未完成计算,且在200秒附近G-mean 才开始急剧增加,再一次表明与RF相比,BLOCK-SDB-RF方法具有更高的计算效率。同时,由图4的(b)、(c)、(d)发现,变量间的不同相关性并不影响BLOCK-SDB-RF在计算速度方面的优势,BLOCK-SDB-RF始终以明显较快的速度达到收敛。然而由表3可见,随着变量间相关性的增加,在对全部特征进行分组降维时受到的干扰也越来越大,因此BLOCK-SDB-RF方法的预测准确率会有明显下降,RF方法的分类准确率也会受到一定程度的影响。但从总体上讲,相比RF方法,BLOCK-SDB-RF的分类准确率更高。 本文的实证数据是由音乐流媒体服务商KKBOX提供的日志数据,来源于2017年Kaggle平台举办的一场数据挖掘竞赛。该竞赛向大众提供了训练集合表、测试集合表等按时间顺序划分的日志数据与歌曲信息表、用户信息表、歌曲补充信息表共5个表格。为便于分析,本文对该竞赛提供的5个表格数据进行了清洗与整合,并结合特征工程从用户、歌曲及两者交互三个维度提取不同的特征变量,最终得到样本量为100 000、特征维数为1 089的大规模数据集(除去歌曲id、用户id及因变量“是否重复听歌”三个变量)。数据集的整体结构如图5所示,部分变量及含义见表4。 图5 特征维度示意图 表4 数据特征示例(部分) 文章以“用户重复听歌”事件作为准则判断用户对歌曲是否喜爱,即如果用户在第一次点击某首歌曲之后的一个月里触发“重复听歌”事件,则认为用户喜爱该歌曲,将因变量记为1,否则记为0。考虑到数据集样本量大,特征维数高,本文利用BLOCK-SDB-RF方法在训练集上建模,并在测试集上对用户是否会重复听歌进行预测,以期更好地了解用户的听歌偏好。 在建模之前,对用户、歌曲及两者交互三个维度下变量间的相关关系进行初步探索。考虑到变量间的关系并不能由简单的线性相关进行刻画,文中采用了秩相关系数,部分变量间的相关关系如图6所示。图6中带斜线阴影部分表示负相关,未带斜线阴影部分代表正相关,颜色的深浅表示变量间相关关系的强弱,颜色越深,意味着相关关系越强。 结果显示,用户点击的来源信息(X26,X25)即用户通过点击电台、专辑或者其他方式进入该歌播放的比例、用户最后听歌时间(X91)、歌曲流行程度(X23)对因变量Y是否重复听歌的影响比较显著。歌曲-用户交互维度中,特定用户对歌手(X29)、作曲家(X30)、作词人(X31)的喜好也对Y有影响,但是相关性较之用户维度、歌曲维度的变量更弱。另一方面,不同特征间也具有一定程度的相关关系,比如X20用户对发行年份的偏好、X21某歌曲计数、X22某用户计数三个特征间具有较强的正相关关系等。但是考虑到在数值模拟部分发现,特征变量间的相关性并不会影响BLOCK-SDB-RF方法在计算时间方面的优势,因此仍然可以使用该方法对数据进行建模、预测。 图6 部分变量间的秩相关图 将清洗后的数据集按照3∶1划分为训练集与测试集。在训练集上分别利用RF、BLOCK-SDB-RF两种方法建立模型,然后在相应测试集上进行预测,得到实证结果如下。 1.相同时间内计算结果对比 为节约时间成本并方便结果对比,同样借鉴Sengupta等的思路,考虑在1 000秒时间内哪种方法能以更快的速度达到合理准确的结果,最终结果如图7所示[6]。图7中横轴为time,表示计算消耗的时间;纵轴为指标G-mean,实线表示BLOCK-SDB-RF方法,虚线表示RF方法。结果显示,RF方法在测试集预测结果的G-mean指标于700秒附近开始急剧增加并达到一定高度,而BLOCK-SDB-RF方法在400秒附近就发生了类似变化,表明BLOCK-SDB-RF方法在计算时间方面具有一定优势。 图7 实证数据结果对比图 2.不限制计算时间的结果对比 当不限制计算时间时,分别使用RF、BLOCK-SDB-RF方法对测试集做出预测,其中RF方法共建立200棵决策树,得到预测结果见表5。结果显示,BLOCK-SDB-RF方法预测的总体准确率为75.9%,G-mean为59.5%,与RF方法得到的计算结果基本一致。但是从计算时间角度看,BLOCK-SDB-RF方法共消耗计算时间13.53分钟,与RF方法建立200棵决策树需要耗费的20.19小时相比,大大降低了计算成本。特别是在更加大型的推荐系统中该方法的优势将更加明显。 表5 预测结果 3.变量重要性分析 在BLOCK-SDB-RF实施过程中,将分组考察各个特征变量对分类结果的贡献,并以此作为该特征变量的重要性度量。表6为重要性排名前10的特征变量及其与因变量Y的秩相关系数。 由表6可见,BLOCK-SDB-RF方法下重要性排名前10位的特征变量,比如X23某歌曲计数(即歌曲的流行程度)、X25某用户不同界面来源比例、X26某用户app上音乐入口比例等,与因变量Y的秩相关系数也较高,分别为0.184,0.060,0.134。这与建模之前初步探索得出的结果大体一致,即与因变量Y越相关的变量越能解释Y中包含的信息。相比而言,用户、歌曲维度下的变量比两者交互维度的变量更重要。 表6 变量重要性排名与秩相关系数 本文以随机森林算法为基础,结合“分治”思想提出了大规模随机森林算法,对样本量大、特征维度高的数据集进行分析。在尽量保证算法有效性的前提下,解决了大规模数据带来的计算效率问题。通过数值模拟与实证分析表明,随着数据量、特征维度的增加,该方法在计算时间上的优势愈发明显,同时变量间的相关性对该方法在计算效率方面的优势影响并不显著。然而,在应用方面BLOCK-SDB-RF方法仍然存在一些问题有待进一步探讨。 第一,本文以随机森林为基础算法,通过同时对样本维度和特征维度进行处理,将其内嵌到本文提出的分析框架中以应对大规模数据带来的计算效率的挑战。事实上,本文提出的大规模数据分析框架并不局限于随机森林算法,其他常用的机器学习算法比如支持向量机(SVM)等均可以嵌进其中。 第二,KKBOX提供的日志数据实际上是一个不平衡数据,其中包含的正样本(因变量为“重复听歌”的样本)数量远远大于负样本(因变量为“未重复听歌”的样本),并且文中并没有针对这种情况做出处理,因此在实证分析部分得到的预测结果会出现真阳性率较高,真阴性率较低的情况。事实上,这种不平衡数据集在实际生活中非常普遍,比如贷款违约预测的数据、医疗数据等,针对这种数据在因变量上分布不平衡的问题,可以考虑通过数据层面或者算法层面的调整解决[17-18],比如在数据层面上利用过采样、欠采样将不平衡数据调整为平衡数据,或者类似调整的支持向量机算法等直接对算法进行修正以适应不平衡数据。 第三,变量间的相关性虽然并不影响BLOCK-SDB-RF方法在计算时间方面的优势,但随着相关性的增加,预测结果的准确率会因此有所下降。即该方法在提升计算效率的同时,有时会以牺牲预测精度为代价。特别地,在实际数据中,变量间具有一定程度的相关性总是不可避免的。这一方面要求我们在预测的准确率和计算效率上做出权衡,另一方面也需要考虑当变量间具有较强的相关性时,如何减轻变量选择结果受到的干扰,为未来研究指明方向。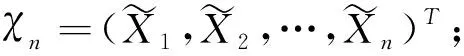
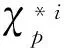
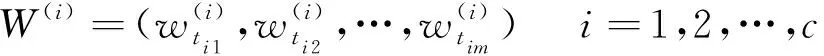
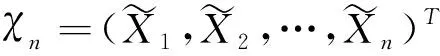
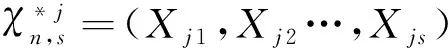
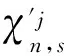
三、数值模拟
(一)不同样本量

(二)不同特征维数
(三)不同变量相关性

四、实证分析
(一)初步探索

(二)实证结果
五、讨论
