网络Meta分析研究进展系列(二十):网络Meta分析的样本量计算及精确性评估
2022-03-15杨智荣武珊珊董圣杰张天嵩田金徽孙凤
杨智荣,武珊珊,董圣杰,张天嵩,田金徽,孙凤
与其他类型的临床研究一样,Meta分析也存在样本量和检验效能的问题[1]。当纳入的样本量不足时,Meta分析的检验效能较低,所估计的效应值可能会出现假阴性或假阳性的情况,结果的精确性较低(体现在置信区间的跨度较大)[2]。
近年来,Meta分析的样本量和检验效能的问题逐渐得到关注。在传统Meta分析中,通常采用试验序贯分析来估算样本量[3]。它按照纳入研究的发表时间顺序进行累计,通过调整随机误差和研究间异质性,最终估算得出确切结论时所需要的最小信息量(即纳入研究对象的总数量或结局事件发生数)。在网络Meta分析(network meta-analysis,NMA)中,也同样存在样本量与统计效能计算的问题[4]。通过模拟研究发现,NMA合并结果往往因统计效能不足而缺乏可信性,研究者及证据使用者应谨慎地评价NMA合并结果的统计效能,这对判断证据的真实性和临床价值尤为重要。
目前,NMA的样本量及统计效能的计算方法主要有三种:有效合并研究数量法、有效样本量法和等效样本量法[4,5]。在此基础上,研究者可进一步评价证据的精确性[5]。下面以我们课题组发表的一篇NMA为例[6],介绍上述各种样本量计算方法的使用(证据网络结构如图1)。该例子是以二分类指标作为结局,下述所有方法也适用于连续性结局指标。
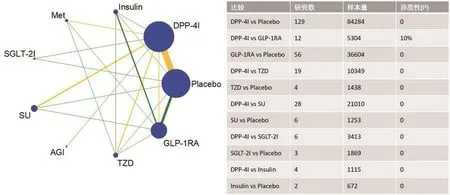
图1 证据网络结构图
为了评估GLP-1RA和DPP-4I两类新型降糖药在2型糖尿病患者中的心血管事件,该NMA纳入了281项治疗时间≥12周的随机对照试验(约180 000例患者),以心血管死亡、心肌梗塞、中风和心力衰竭等事件作为心血管复合结局(简称MACE)[6]。研究发现,GLP-1RA与安慰剂和SU相比,结局风险降低,比值比(OR)分别是0.89(95%CI:0.80~0.99)和0.76(95%CI:0.59~0.99),而 DPP-4I与安慰剂相比未显示出统计学差异(OR=0.92,95%CI:0.83~1.01)。研究的结论是,与SU或安慰剂相比,GLP-1RA可降低MACE发生风险,而DPP-4I则对MACE发生风险没有影响。但该NMA的结论是否有足够的样本量和检验效能来支撑?这就需要通过以下方法进行回答。
1 有效合并研究数量法
应用有效合并研究数量法进行计算时,前提假设是纳入合并的各个研究方差相等且具有同质性,即认为纳入研究的对象均来自同一个总体。其计算主要包括以下步骤[4]:
1.1 根据间接比较的研究数目来确定精确度比率先假设干预措施A和B比较的效应值均来自间接比较A和C的nAC个研究与B和C的nBC个研究,且每个研究的效应值方差均为v,那么根据间接比较的方差计算公式,A和B比较的效应值方差为

又假设有k个(k=nAC+nBC)A和B直接比较的研究,每个研究的效应值的方差均为v,在不存在异质性的情况下,那么由固定效应模型估算的A和B合并值的方差就为
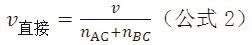
而所谓的精确度比率R,就是公式1和2之比,即

该比值表示在间接比较中需要多少个AC和BC比较的研究才能达到一个AB直接比较的效应值的精确度。根据公式3,当nAC和nBC的比值为1:1时,可算得R为4;当比值为1:2时,R为4.5;当比值为1:3时,R为5.33。如此类推,可计算任意比值下的R(表1)。
上述实例当中(图1),DPP-4I和安慰剂分别与GLP-1RA比较的研究分别有12和56个,按照上述公式3,可知R为6.88。即在满足纳入的各个研究的效应值方差相等且具有同质性的前提下,对于DPP-4I与安慰剂的比较来说,需约7个间接比较的研究才能达到1个直接比较的效应值的精确度。
1.2 计算由间接比较所贡献的有效合并研究数量该指标是指在已有间接比较的研究数目下,可等同于多少个类似的直接比较研究。可根据间接比较的实际纳入研究和精确度比率计算,即
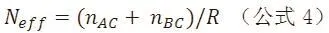
例如上述实例当中(图1),对于DPP-4I与安慰剂的比较来说,由以GLP-1RA作为共同比较组的间接比较所贡献的有效合并研究数约为10个(按公式4计算,结果为9.88)。
为快捷地进行近似计算,Thorlund等制定了有效合并研究数量的表格(表1)[4]。研究者通过查表,可迅速知道NMA中的间接比较贡献了多少有效合并研究数量。例如上述实例当中(图1),以GLP-1RA作为共同比较组的间接比较的研究数约为1:5(12和56的比值),合计68个研究,与表中的72(12:60)的数值最为接近,所对应的有效合并研究数为10个。与上述公式4的计算结果类似。大部分的间接比较都能在表1中找到近似的有效研究合并数,如果出现极端的间接比较研究数比值(如1:20),超出了表1的范围,此时需根据公式3和公式4来确定有效合并研究数。
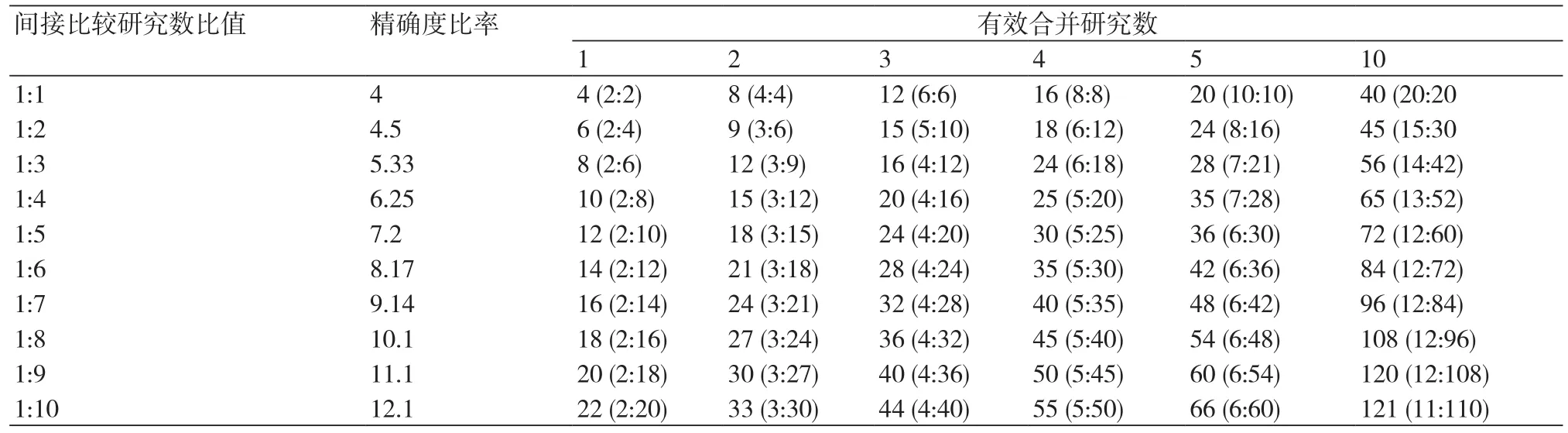
表1 有效合并研究数与所需的间接比较研究数
有效合并研究数量法只适用于粗略估计间接比较中的有效研究数。如果需要更精确的估算,则应进一步计算有效样本量或等效样本量(即研究对象数目),具体见下述。
2 有效样本量法
该方法将NMA证据网络中的每一个比较对视为一个临床研究,通过估算每一个比较对的有效样本量来计算间接比较的统计效能和精确性[4]。该法包括非校正和异质性校正两种方式,其计算主要包括:①根据样本量比值计算精确度比率;②分析各比较组是否存在异质性;③对具有同质性的比较组,用总体间接样本量乘以精确度比率即可获得有效间接样本量,对于存在异质性的比较组,则通过异质性校正因子对实际样本进行处理后,再计算有效间接样本量。以下介绍常用的通过有效样本量法来计算检验效能的步骤。
在图1的由DPP-4I、GLP-1RA和安慰剂三种干预构成的闭合环,DPP-4I与安慰剂、DPP-4I与GLP-1RA、GLP-1RA与安慰剂直接比较的样本量分别为84284、5304和36604,I2分别为0、10%和0。现在需要计算DPP-4I与安慰剂在此闭合环的NMA中的检验效能。
第一步:计算直接比较所需的样本量。在不考虑异质性的情况下,计算方法等同于一项RCT的样本量计算
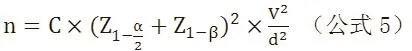
d为预期效应值(如两组结局发生率的差值),V是预期效应值的方差(若结局为二分类时,为两组结局发生率的平均值),和Z1-β分别是正态分布在和1-β百分位上的Z值。一般假设两组样本量相等,此时C=4。若存在异质性,此时需要在n的基础上乘以异质性校正系数,H=I2。
根据上述公式,若预计安慰剂组的MACE事件发生率为2%,DPP-4I组的发生率能降低20%(即发生率为1.6%)时认为有实际意义,α=0.05,1-β=90%,根据公式5,在不存在异质性的情况下,图1中DPP-4I与安慰剂直接比较的所需样本量为
n=4×(1.96+1.28)2×[(0.02+0.016)/2]×[(1-(0.0 2+0.016)/2)]/(0.02-0.016)2=46389。
第二步:计算间接比较的有效样本量nind,也分为存在和不存在异质性两种情况。若不存在异质性时,可基于AC和BC的间接比较(如图1中的DPP-4I与GLP-1RA、安慰剂与GLP-1RA)计算AB(如图1中的DPP-4I与安慰剂)间接比较的有效样本量:
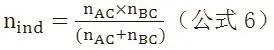
若有异质性存在,则需要先对nAC和nBC进行调整,即分别乘以相应的1-I2。然后把调整后的nAB和nAC代入上述公式6。
例如,图1中nAC=5304×(1-0.10)=4774(I2=10%), nBC=36604(I2=0),代入公式6,即得:
nind=(4774×36604)/(4774+36604)=4223。
同理,我们可以基于其他闭合环计算nind。根据图1中的数据和公式6,可得出DPP-4I-TZD-安慰剂、DPP-4I-SU-安慰剂、DPP-4I-SGLT-2I-安慰剂、DPP-4I-Insulin-安慰剂这四个闭合环为DPP-4I与安慰剂比较所贡献的nind分别为1263、1182、1208和419。
第三步:计算合计的有效样本量N。此时只需把DPP-4I与安慰剂直接比较的样本量(84284例,图1)和间接比较的有效样本量相加,即N=84284+4223+1263+1182+1208+419=92579,多于经公式5计算得到的所需样本量46 389,说明NMA实际纳入的样本量已满足DPP-4I与安慰剂比较的统计学要求。
第四步:计算检验效能1-β。
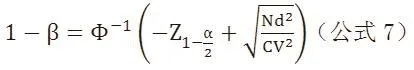
把上述所有参数代入公式7,得到1-β=98%。这说明基于当前样本量的NMA,有足够的检验效能发现DPP-4I与安慰剂比较的MACE事件发生率的差异。
3 等效样本量法
近年来,随着GRADE证据评级系统的发展,GRADE工作组对NMA结果的精确度评价作了相应的规定,提出等效样本量的计算方法[5]。
该方法首先忽略整个证据网络中的直接证据和间接证据,将NMA的效应估计值和CI当作单个研究的结果,重点关注要达到该CI的精确度所需要的样本量,然后在特定基本假设下,反推计算产生该NMA效应估计值的等效样本量,跟所需样本量(通过公式5计算)作对比,从而确定等效样本量是否满足需求。以下分别介绍以RR、OR和均数差作为效应量时的等效样本量计算。
(1)假设纳入NMA的均为两组样本量相等的试验,log(RR)的标准误可计算为:
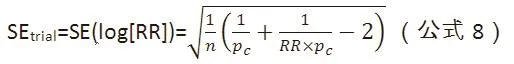
其中,n是每组样本量,Pc是对照组中观察到的结局发生比例,RR是相对风险。NMA估计值log(RR)的标准误可以根据CI上、下界来计算:
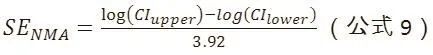
假设两个标准误相等,即可算出样本量n:

Pc可通过网状结构中的相关比较组的比例(经Meta分析合并)来估计,也可通过简单计算结局发生数和患者数来近似估计Pc。
(2)假设纳入NMA的均为两组样本量相等的试验,log(OR)的标准误可以估计为:
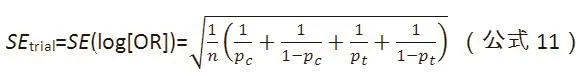
其中n为每组样本量,Pc为对照组发生结局的比例,Pt为观察组发生结局的比例。Pt也可以由Pt=Pc*OR/(1-Pc+Pc*OR)来计算,NMA估计值log(OR)的标准误可以根据CI上、下界来计算:
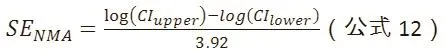
假设两个标准误相等,可以求解n:
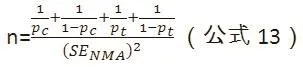
(3)假设纳入NMA的均为两组样本量相等的试验,两均数差的标准误可以估计为:

其中n为每组的样本量,SD为组内合并标准差(可采用所有k个比较臂的SD的合并值),NMA均数估计值的标准误可以根据CI上、下界来计算:

假设两个标准误相等, 可以求解n:

例如,图1的实例当中, DPP-4I与安慰剂相比MACE事件发生率的差异没有统计学差异(OR=0.92,95%CI:0.83~1.01)。安慰剂组MACE事件的发生风险(各研究安慰剂组的中位数)为1.2%。根据公式11至13,可计算出满足OR、基线风险和CI的单个研究样本为每组70 506例,因此该NMA案例其估计值对应的等效样本量为141 012例,多于经公式5计算得到的所需样本量46 389,说明当前等效样本量满足统计要求。
4 精确性的评级
样本量的大小与效应估计值的精确性紧密相连,样本量越大,精确性越高。在GRADE证据分级中,效应估计值的精确性是其中重要的考虑因素之一[7]。
按照NMA的GRADE分级规定,证据精确性的降级有三种情况[5]。①当效应估计值的95%CI的上限和下限之比小于3(如实例中的效应估计值的95%CI为0.83~1.01,上下限比值为1.22),此时需要计算等效样本量和所需样本量(通过公式5计算),若等效样本量大于所需样本量,则证据的精确性不降级(例如图1实例中的DPP-4I与安慰剂MACE发生风险的比较),否则应降一级。②当效应估计值的95%CI的上限和下限之比大于3时,不需要计算等效样本量,因为这种情况下过大(远大于公式5中的V),使得由公式10、13、16计算得到的等效样本量过小,一般难以满足由公式5计算的所需样本量,因此证据的精确性应降两级。③当效应估计值的95%CI极其宽,不需要计算等效样本量,直接把证据的精确性降三级[8]。
需要注意的是,GRADE证据分级对精确性的评价不一定要依赖等效样本量,也可以设定跟临床决策相关的效应阈值,然后根据95%CI是否包含该阈值来进行分级(具体请查看GRADE相应的文献[5])。
5 讨论
本文综述了NMA样本量计算的常用方法。目前这些方法都是采取简便的近似计算,帮助研究者评估NMA所估计的效应值是否满足检验效能的要求[4,5]。
除了只是简便的近似计算以外,上述各种计算方法都有各自的前提假设和优缺点[4,5]。有效合并研究数量法假设每个研究的样本量相等,效应值的方差相等,且不存在异质性。该方法只能非常粗略地估计在间接比较中需要纳入多少个研究才能达到一个直接比较研究的效应估计值的精确度。在实际操作中,更多使用有效样本量法和等效样本量法。这两种方法均考虑以研究个体作为单位计算样本量,而且均把NMA看作是单个研究,然后基于特定的假设来计算有效样本量或等效样本量;主要区别在于,前者是基于间接比较的样本量换算成与直接比较相当的样本量,后者则是基于NMA效应估计值的置信区间反推直接比较的样本量。此外,前者方法还可进一步对可能存在的异质性进行调整,而后者已把异质性的大小蕴含在随机效应模型所估算的置信区间之中。由于计算原理不同,这两种方法的结果可能会存在一定差异。研究者可根据实际情况选取一种或同时使用两种方法进行样本量计算。若这两种方法所得到的样本量均大于所需样本量,更有理由说明当前NMA中某两种特定干预的比较具有足够的检验效能。如本文的实例,对于DPP-4I和安慰剂的比较,不管是有效样本量法还是等效样本量法,计算结果均大于所需样本量,因此在对证据的精确性进行评价时可不降级。
目前已经发表的NMA,包含样本量计算的研究并不多。但如果要回答NMA是否有足够的检验效能,则应对样本量进行计算,包括所需样本量和NMA的有效或等效样本量。在使用GRADE分级系统对证据的精确性进行分级时,效应估计值的精确性跟样本量密切相关,分级时可能也会涉及样本量的计算。建议研究者在进行NMA后应评估当前样本量是否满足检验效能的要求,并对效应估计值的精确度性进行评价。
