复杂部件二维保修费用优化模型研究

王 谦，程中华，白永生，张 芳，时晓文，张建卿

(1.陆军工程大学石家庄校区，河北 石家庄 050003；2.陆军第九综合训练基地，河北 张家口 075000；3.32178部队科技创新研究中心，北京 100012；4.32654部队，山东 济南 250000)

在当前激烈的产品市场竞争中，产品保修服务在营销中发挥着越来越重要的作用，能够让顾客满意的售后服务已成为各个企业间相互竞争的一个重要因素。按照保修服务的截止期限，将保修服务分为一维保修、二维保修和多维保修策略等[1]。一维保修是指产品保修期以单一指标确定的，通常为日历时间或使用时间之一。二维保修指产品保修期由两个指标共同确定，通常为使用时间和使用程度。多维保修，则是指产品保修期由超过两个指标共同确定。目前，二维保修策略已经广泛地应用于很多二维保修产品保修服务中。为了降低保修期内维修费用、提高可用度，当产品使用一段时间之后，进行预防性维修是必要的。目前，在很多产品保修策略中，也逐渐由单一的修复性维修为主转变为包含预防性维修的策略。通过研究，很多国内外学者已证明了这种策略的优越性。

在现有文献[2-5]中，提出的保修策略都是在保修期内进行单一预防性维修，少数文献涉及到复合预防性维修策略。仅有Liao提出在保修期内进行的预防性维修包括完全维修、不完全维修和预测性维修[6]。但是，目前还没有文献提出过两种不同程度不完全维修的组合。而这样的组合，在实际保修服务中有很大的应用空间。笔者所提出的预防性维修，包含了两种程度的不完全维修。

在现有的文献中，大部分是研究复杂部件在一维保修期内的费用模型，或者单部件二维保修期的费用模型，研究复杂部件二维保修的文献相对较少。方瑛等将复杂串联系统作为研究对象，考虑不同单部件的重要程度对维修费用的影响，建立了考虑定期更换的预防性维修策略[7]。杨云聪对两部件串联系统进行研究，提出计划型和机会型预防维修策略，建立了费用模型、可用度模型和可调节的多目标模型[8]。白永生考虑复杂部件一维保修预防性维修的典型维修工作组合优化模型和复合维修周期优化模型[9]；Khatab等提出在维修时间和维修资源有限的条件下，对复杂部件中各单部件选择性维修，建立费用模型[10]。Duan等将多部件系统组成分为重要部件和不重要部件，从节省维修设备的安装费用和共同维修费用角度出发提出进行机会维修，以长期平均成本最小为目标建立费用模型[11]。李欣玥考虑了一维保修期内，二维预防性维修的组合优化[12]。

笔者将复杂部件保修费用的研究从一维保修期扩展到二维，并对保修期内二维预防性维修工作进行了组合优化。从现有文献可以看出，对二维保修期内复杂部件维修费用的研究较少，这将是笔者所要研究的主要内容。

1 模型提出

笔者提出在对单部件联合预防性维修的基础上，考虑复杂部件二维保修中预防性维修组合优化模型。其中，所进行的预防性维修均为不完全维修。

按照维修后产品的恢复程度的高低，将维修分为三类：最小维修(ABAO)、完全维修(AGAN)和不完全维修。最小维修，每次修复将产品恢复到故障之前的水平；完全维修，每次修复将产品恢复为像新产品一样；不完全维修，其修复程度介于前两者之间。研究认为，通过维修可以降低产品的虚拟工龄，从而提高产品可靠性。通过维修，将产品在该时刻的故障率降低到实际工龄之前某一时刻的故障率，之前的这一时刻就是虚拟工龄。例如，对已经使用1年的某大型设备进行维修，维修后，该设备的可靠性得到恢复，如同仅仅使用了8个月的设备一样，则8个月就是该设备的虚拟工龄。不完全维修对产品虚拟工龄的影响，通常有两种假设：一是缩减了上一预防性维修间隔期内的虚拟工龄；二是缩减此次预防性维修之前的整个虚拟工龄。笔者采用第2种假设，在这种假设中用到比例年龄倒退模型[13]，在许多文献中也用到同样的假设模型[14]。假设在T时刻对产品进行不完全预防性维修，ξ为修复因子，T-和T+分别表示维修前、后产品的虚拟工龄。则维修后虚拟工龄可以表示为T+=ξT-，故障率的变化为λ(T+)=λ(ξT-).在进行不完全预防性维修中，不同的修复程度对应不同修复因子，修复程度越高，对产品的恢复效果越好，所对应的维修成本也会高，这与实际情况是相符的。

1.1 单部件联合预防性维修费用模型

建立修复程度不同的预防性维修条件下单部件保修费用模型，确定出最低保修费用和其对应的预防性维修间隔期。在现有的文献研究中，对部件进行的预防性维修均采用单一修复程度，但在实际保修工作中，不同维修主体的维修水平是有区别的，对同一个部件进行预防性维修后，部件的恢复程度有所不同。在此前提下，笔者提出对部件进行两种不同修复程度的联合预防性维修。假设厂家的维修水平高于用户的维修水平。

1.1.1 模型描述

二维保修期(Tw,Uw)内，rw为部件的设计使用率，rw=Uw/Tw.以(T0,U0)为间隔期进行周期性不完全预防性维修，T0和U0分别是二维不完全预防性维修的时间和使用度间隔，设r0=U0/T0,进行预防性维修后，降低了部件的故障率。规定保修期内进行N1次预防性维修，在第N2次由厂家执行(N2=int(N1/2)+1).ξ1、ξ2分别为用户和厂家进行预防性维修后的修复因子，Cp1、Cp2分别为用户和厂家进行预防性维修的费用，D为每次预防性维修的准备费用和导致的系统停机损失。部件的初始故障率为λ(t|r)，第n次和第n+1次预防性维修间隔期内的故障率为λn(t|r)，(n=[1,N1-1]).保修期内，部件出现故障后，由厂家负责进行最小维修，即维修前后部件故障率不变，Cf为部件故障后的维修费用。在现有研究中，二维故障率主要有3种表示方法，分别是双因素变量法、复合尺度法和使用率法，使用率法应用比较广泛。假设在保修期内单个部件的使用率保持不变，但是不同的用户其使用率不同。对于批次部件而言，使用率是随机变量。假设通过先前部件使用的反馈信息和调查了解到该分布，使用率的分布函数与概率密度函数分别为G(r)和g(r).假设部件的使用度u是使用时间t的线性函数，对于给定的使用率r，有u=r×t.部件在使用率为r时故障率函数为λ(t|r),表达式采用[15]λ(t|r)=θ0+θ1r+θ2t2+θ3rt2,θ0,θ1,θ2,θ3为故障率参数，其具体值可根据相应部件的历史使用故障率进行估计得到。

1.1.2 模型建立

使用率r的变化，对预防性维修间隔和保修期限有较大的影响。随着r取值范围发生变化，预防性维修间隔和保修期限可分为6种情况，如表1所示。

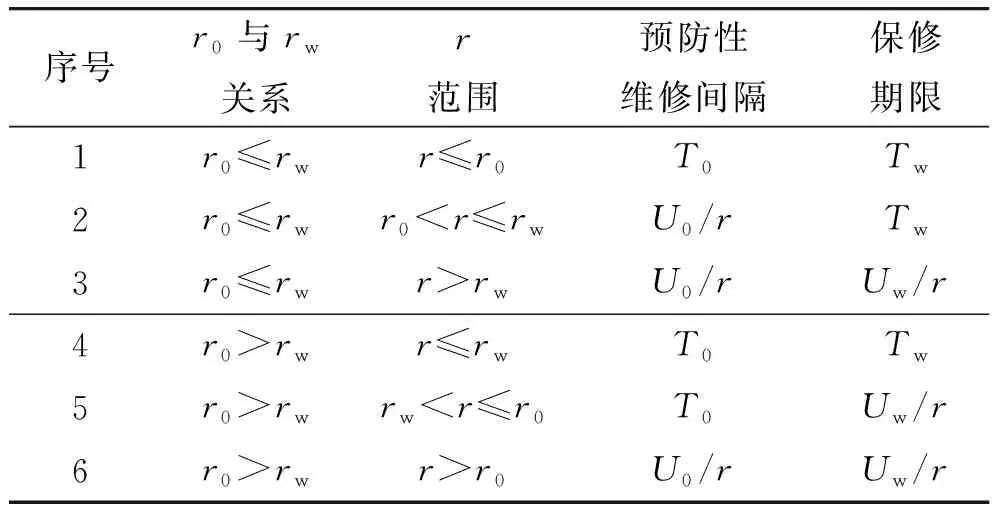
表1 不同条件下预防性维修间隔和保修期限

如果r0≤rw，如图1所示，可分3种情况。

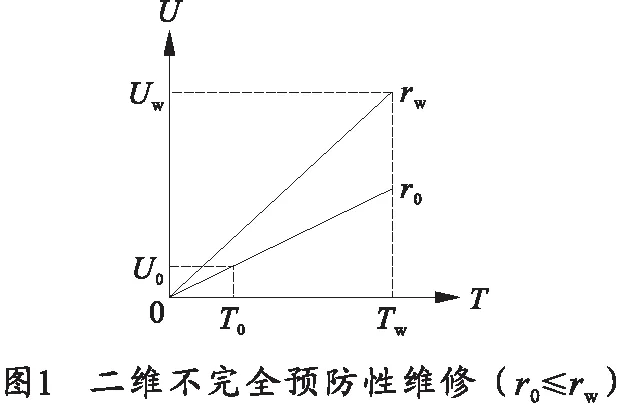
在情况1中，当r≤r0时，预防性维修间隔期为T0，保修截止期限为Tw，N1=int[Tw/T0].

故障率的表达式为

(1)

该条件下，保修期内的费用为

C1(T0,U0)=(Cp1+D)(N1-1)+(Cp2+D)+

(2)

在表1中的其他情况下，故障率表达式与情况1类似，在计算保修费用时，主要是对预防性维修间隔和保修期限进行区别。推导过程不再赘述，仅给出其余5种情况下保修费用的表达式，依次为

C2(T0,U0)=(Cp1+D)(N1-1)+(Cp2+D)+

(3)

C3(T0,U0)=(Cp1+D)(N1-1)+(Cp2+D)+

(4)

C4(T0,U0)=(Cp1+D)(N1-1)+(Cp2+D)+

(5)

C5(T0,U0)=(Cp1+D)(N1-1)+(Cp2+D)+

(6)

C6(T0,U0)=(Cp1+D)(N1-1)+(Cp2+D)+

(7)

由式(2)～(4)知，当r0≤rw时，保修期内维修费用期望值为

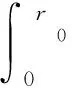
(8)

由式(5)～(7)知，当r>rw时，保修期内维修费用期望值为

“双创”教育在本质上是一种全面发展的素质教育，“双创”人才培养要求高校深化教育教学改革，高校应在改革过程中循序渐进。高校应深入理解“双创”人才培养理念，不可停留在传统教育以技能为主的初级层面。通过技能与素质教育，如同培养学生职业技能一样，力争让每位学生具备“双创”核心素养，即全面发展的高层次人才素养。最终以“双创”为核心，重构技能与素质融合的多元框架体系，切实增强学生的“双创”意识及能力。推动“双创”人才培养高质量发展，有利于进一步增强毕业生创业带动就业的能力，有利于提高科技创新和产业发展活力，对增强经济发展内动力具有重要意义。

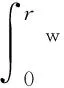
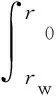
(9)

1.2 复杂部件联合预防性维修费用组合优化模型

在建立单部件联合预防性维修费用模型的基础上，求得各个单部件最低保修费用，并得到对应的预防性维修间隔期。在此基础上，将不同部件的预防性维修工作进行组合优化，建立组合后的费用模型。

1.2.1 模型说明

将由L个单部件组成的串联系统为研究对象。按照1.1中提出模型，经计算得出在二维保修期内，各单部件分别以(T1,U1)、(T2,U2)、…、(TL,UL)为间隔期进行预防性维修，可使各部件保修费用最低。针对使用率一定条件下的单部件，其预防性维修间隔期是以时间和使用度两个维度之一作为间隔的。但是对于复杂串联系统来说，在某一使用率的条件下，不同部件可能按照不同维度的间隔期进行预防性维修。比如，对于由L个单部件组成的串联系统，可能有A个部件以时间维度的间隔期进行预防性维修，有B个部件以使用度维度的间隔期进行预防性维修,其中,A∈[0,L]，B∈[0,L]，必有关系式A+B=L成立。在不同使用率条件下，其预防性维修的次数不同，因此，需要在不同的维度下进行预防性维修工作的组合。

1.2.2 优化方法

串联复杂部件，在单部件二维预防性维修的基础上，提出多部件组合预防性维修优化模型。方法如下：

(10)

式中，Tsi为调整后部件的使用时间维修间隔期，“[*]”表示对“*”四舍五入取整，组合方式如图2所示。

将各单部件在使用度维度预防性维修间隔期调整为多部件系统的使用度基本维修周期Us的整数倍，即

(11)

式中，Usi为调整后部件i的使用程度维修间隔期，组合方式如图3所示。

2 算例分析

已知某新型复杂部件销售以后，为减少故障次数，降低保修期内费用，需要进行预防性维修。经分析，这一新型复杂部件由5个部件串联组成。通过多年同类型部件使用与维修经验的积累，用户已经具备了一定程度的维修能力。在部件的使用初期，与厂家相比，用户的维修能力还略有差距。因此，按照文中建立的模型，采用厂家和用户两级力量进行相组合的预防性维修。在保修合同中，规定该部件二维保修期限:Tw=5年，Uw为15万公里。各单部件的故障率均服从威布尔分布，部件的故障率为λl(t|r)=θ0iθ1ir+θ2it2+θ3irt2.为简化计算，假设各单部件预防性维修的准备费用和导致的系统停机损失相等，即Di=1 500元(i=1,2,3,4,5),其余参数如表2所示(相关数据可从工业部门的历史数据统计中获得)。

表2 参数设置

其中，ξ1i、ξ2i分别为用户和厂家对部件进行预防性维修的修复因子，Cp1i、Cp2i分别为用户和厂家对部件i进行预防性维修的费用，Cfi对部件进行修复性维修的费用

按照1.1中给出的模型，借助MATLAB软件进行计算，可以得出在二维保修期内不同部件单独进行预防性维修条件下的最优维修间隔期和最低保修费用。经计算可得，各个部件单独进行预防性维修的最优间隔期和对应的费用如表3所示。通过计算，优化之前保修期内复杂系统的总维修费用为40.282 5万元。

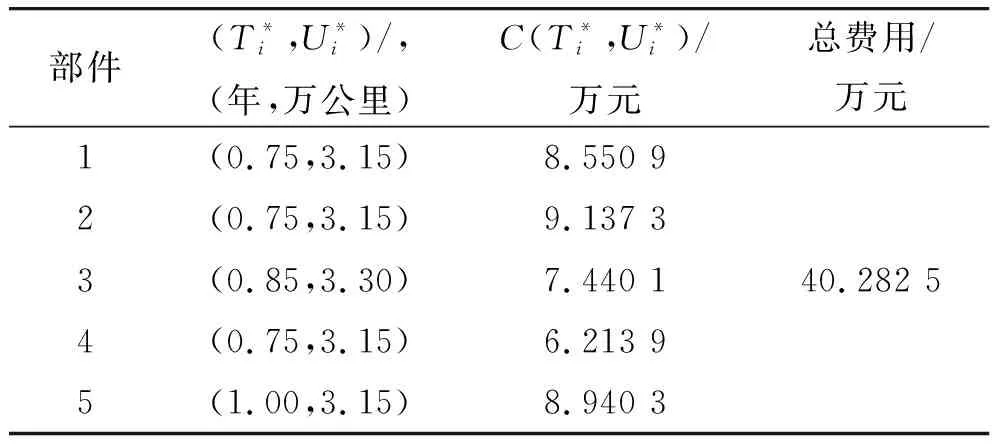
表3 各部件预防性维修的最优间隔期和最优保修费用

按照1.2中给出的优化策略，若进行预防性维修组合优化，计算出不同基本维修周期条件下保修费用，结果如图4所示。

通过结果对比可得，最优基本维修周期为(0.75，3.0)，对应的最低保修费用为37.516 8万元，比优化之前的总费用降低了6.87%.由此可知，所提出的组合优化策略是有效的。

3 敏感性分析

在预防性维修组合优化模型中，主要是通过多个部件组合进行预防性维修来节省总的保修费用，因此，可知预防性维修的准备费用和导致的系统停机损失的大小对组合后的费用有关键性的影响。为了分析影响的大小，进行敏感性分析。

将预防性维修的准备费用和导致的系统停机损失作为变量，其余参数保持不变，得出不同Di条件下的保修费用对比结果，如表4所示。

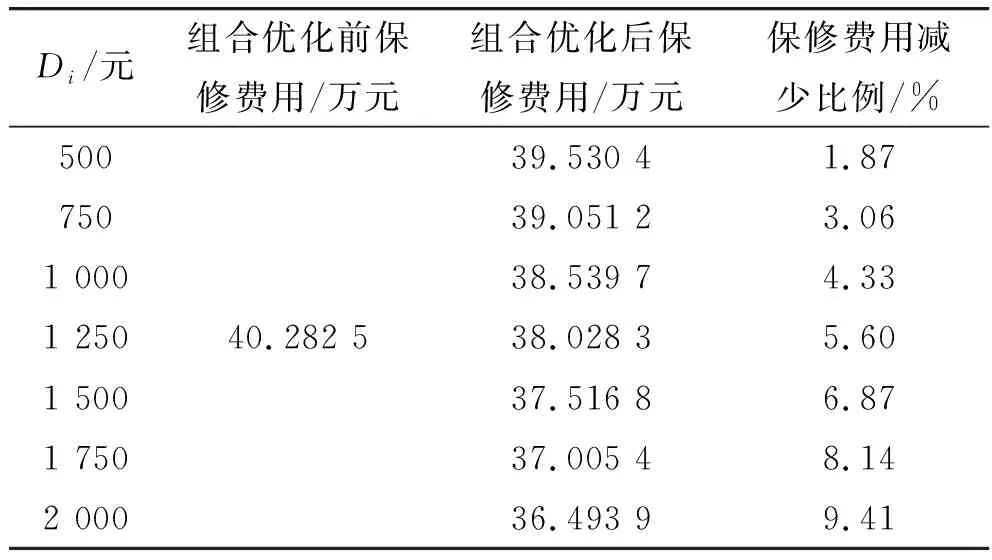
表4 不同Di条件下的保修费用对比

由表4可以看出，当预防性维修的准备费用和导致的系统停机损失逐渐增大时，组合优化后的保修费用随之降低。与组合前的费用相比，保修期内总费用减少的比例逐渐增大。由此可知，当预防性维修的准备费用和导致的系统停机损失越大时，预防性维修组合优化策略的优势越明显。

4 结束语

在研究现有复杂部件二维保修的基础上，笔者提出两级维修力量组合进行预防性维修的保修策略，并对保修期内预防性维修工作进行了组合优化，建立了相应的费用模型。通过复杂串联系统的算例证明了模型的有效性，结果表明提出的组合优化方案可以降低保修期内复杂部件保修费用。从敏感性分析中可知，预防性维修的准备费用和导致的系统停机损失大小对组合优化后的费用有关键性的影响。笔者考虑了对二维保修复杂部件中各个单部件预防性维修间隔期进行优化，降低整个复杂部件的保修费用。各个单部件优化后的预防性维修间隔期还是周期性的，在下一步研究中，可以研究复杂部件中各个单部件的最优预防性维修为非周期性的情况。