高炮侦察系统竞标试验测量精度数据处理方法

史海龙，王晶晶，化斌斌，姜兆义，于 浩

(1.中国人民解放军63850部队，吉林 白城 137001；2.中国人民解放军32183 部队，辽宁 锦州 121000)

在高炮侦察系统竞标试验中，由于浮点数计算问题，数学上等价的算法在数值计算时可能结果不同，造成竞标排名差异。为保证公平性，要求采用同样的数据处理程序处理竞标产品动飞试验得到的数据。因此需要一个通用的数据处理方法，以这种方法编写的通用数据处理程序可以在不改变源代码的情况下对高炮的各种侦察系统进行数据处理。

高炮侦察系统的数据处理方法主要由GJB 3856—1999[1]和GJB 74A—1998[2]定义。跟踪系统，包括跟踪雷达、红外跟踪分系统、电视跟踪分系统的数据处理方法由GJB 3856—1999定义，搜索雷达、目标指示雷达数据处理方法由GJB 74A—1998定义。目前国军标中给出的设计定型试验采用的方法都是将现在点标准值数据变换到被试品坐标系中，然后再进行计算。由于不同侦察系统坐标系定义的不同，难以建立通用方法，每次鉴定试验都要编写新的数据处理程序进行数据处理。

另外，竞标试验与定型试验不同，定型试验多为对单台套设备考核，即使有多台套设备，设备之间的距离也很小，在对标准值进行坐标变换时可忽略地球曲面的影响。竞标试验是对多台套设备进行考核，各竞标设备之间距离可以很大，在进行坐标变换时地球曲面的影响不可忽视。

笔者通过预处理，将输入数据统一为固定格式；通过采用WGS-84坐标系[3]，解决地球曲面影响问题；建立标准坐标系，将被试品数据变换到标准坐标系，解决不同侦察系统坐标系定义不同问题；通过推导标准坐标系下统计结果与被试品坐标系下统计结果的相互关系，建立了一个通用的数据处理方法，并依据此方法，编写了通用数据处理程序。对于依据GJB 3856—1999和GJB 74A—1998进行试验的侦察系统，可以在不改变程序的情况下对数据进行处理。

1 坐标系的建立及精度处理

数据处理关键是时间对齐和空间对齐，时间对齐通过插值实现；空间对齐通过坐标变换实现。数据处理中涉及的坐标系如下：

地心坐标系W定义：采用WGS-84坐标系，记为OW-XWYWZW.

标准值坐标系S定义：原点OS采用一个预先定义的点，XS轴指向东，YS轴指向北，ZS轴垂直向上为正，为右手坐标系。方位角以北0，逆时针旋转为正，高低角以水平面为0，向上旋转为正。

标准站心坐标系C定义：原点OC与武器系统坐标系原点重合，XC轴指向东，YC轴指向北，ZC轴垂直向上为正，为右手坐标系。方位角以北0，逆时针旋转为正，高低角以水平面为0，向上旋转为正。

标准载体坐标系V定义：原点OV与武器系统坐标系原点重合，YV轴与武器系统纵轴平行，指向前方为正，XV轴与武器系统横轴平行，指向武器系统右侧为正，ZV轴与XV轴和YV轴构成右手坐标系。方位角以车体纵轴为0，逆时针旋转为正，高低角以OVXVYV平面为0，向上旋转为正。

被试品(武器系统)坐标系T定义：不同的武器系统定义不同。在定义球坐标时，常见的有两种定义方法：第1种是方位角以南为0，逆时针旋转为正，高低角以载体平面为0，向上为正；第2种是方位角以北为0，顺时针旋转为正，高低角以载体平面为0，向上为正。

地心坐标系、标准值坐标系、标准站心坐标系和标准载体坐标系都是右手坐标系，本文中称为标准坐标系。被试品坐标系根据武器系统的不同，不一定是右手坐标系。

建立坐标系后，测量精度处理方法如图1所示。

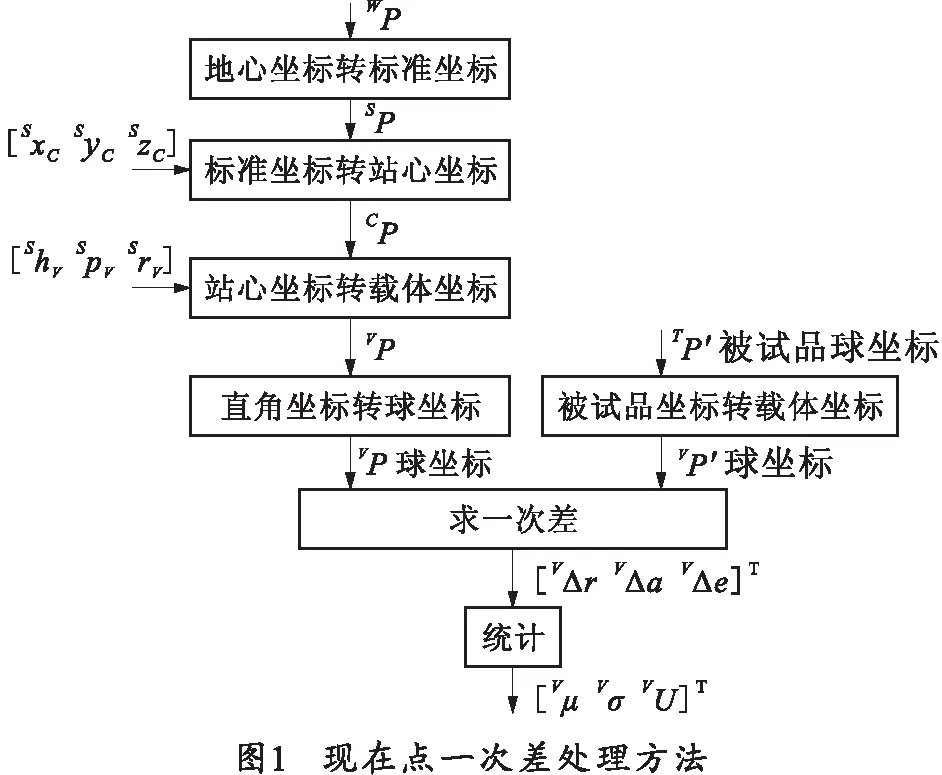
在图1中，由于同时考虑多个坐标系，为简明清晰，采用文献[4]中的符号标记方法，WP表示W坐标系下点P的标准值坐标，VP表示同一个点在V坐标系下的标准值坐标，VP′表示同一个点在V坐标系下由被试的侦察系统测得的数据，(Wxp,Wyp,Wzp)表示W坐标系下点P的XW、YW、ZW轴坐标，VΔr,VΔa,

VΔe表示V坐标系下距离误差、方位角误差和高低角误差。图1中的其他类似符号都采用此规则定义。

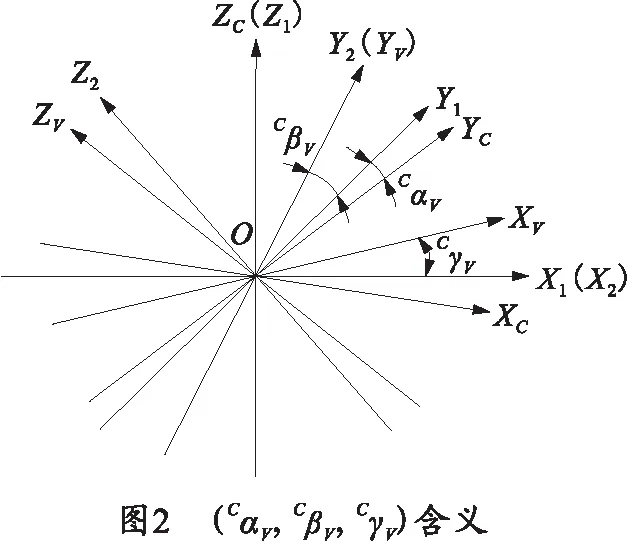
表示两个坐标系相对位置时，如C坐标系下V坐标系的位置，用(CxV,CyV,CzV,CαV,CβV,CγV)表示，(CxV,CyV,CzV)表示C坐标系下V坐标系原点坐标，(CαV,CβV,CγV)表示C坐标系下V坐标系的姿态。(CαV,CβV,CγV)的含义用图2进行详细说明。

在图2中，C坐标系与V坐标系原点重合，简记为O，C坐标系绕ZC轴旋转CαV得到新坐标系O-X1Y1Z1，O-X1Y1Z1绕X1轴旋CβV转得到坐标系O-X2Y2Z2，O-X2Y2Z2绕Y2轴旋转CγV得到V坐标系OV-XVYVZV.CαV、CβV及CγV都是逆时针旋转为正。在试验中，(CαV，CβV，CγV)通常叫做航向角、纵摇角和横滚角。

则图1表示的变换过程为：将地心坐标系下目标坐标的标准值数据WP依次变换为标准值坐标系下坐标SP、标准站心坐标系下坐标CP、标准载体坐标系下坐标VP，然后变换成球坐标，被试品坐标系下的被试品数据TP′变换到标准载体坐标系下坐标VP′，计算一次差，得到一次差后，可通过GJB 74A—1998或GJB 3856—1999统计出V坐标系下系统误差Vμ、均方差Vσ和均方根误差VU.图1省略了时间插值，可参考相关文献[5-6]。

2 坐标系转换

2.1 WGS-84坐标转标准值坐标

WGS-84坐标系常用WB(纬度)、WL(经度)和WH(大地高)表示坐标。要将之转化为标准值坐标系下坐标。

首先转化为以地心为原点的直角坐标：

(1)

式中:e为椭球第一偏心率,

e2=0.006 694 379 990 13;

(2)

(3)

地心直角坐标转T0坐标系:

(4)

式中：T0表示一个坐标系,原点与标准值坐标系原点重合，三坐标轴平行于地心坐标系；(WxS,WyS,WzS)为标准值坐标系原点在地心直角坐标系下的坐标。

T0坐标系转标准值坐标系：

(5)

式中,T0SH表示T0坐标系到S坐标系的变换：

(6)

式中,WBS、WLS表示W坐标系下S坐标系原点的纬度和经度。

则已知目标P经纬度坐标(WBp,WLp,WHp)，标准值坐标系原点经纬度坐标(WBS,WLS,WHS)，通过式(1)可得到直角坐标(WxS,WyS,WzS)和(Wxp,Wyp,Wzp)，结合式(4)～(6)可以得到地心坐标转标准值坐标系下坐标公式：

(7)

2.2 标准直角坐标转站心坐标

2.2.1 站心坐标计算

得到数据后，可以计算在标准站心坐标系下坐标CP:

(8)

式中,[SxCSyCSzC]表示标准站心坐标系原点在标准值坐标系下的坐标。

2.2.2 地球曲面引起的误差

式(8)给出的变换公式主要应用在两个坐标系距离较近的情况，在这种情况下，认为两个坐标系所在位置的重力线是平行的。

对于两个坐标系距离较远的情况，两个坐标系所在位置的重力线不平行，还要考虑地球曲面引起的误差。

如在图3中，当A点和B点高程相同时，如将地表视为平面，则B点在A为原点的坐标系中坐标为(AxB,AyB,0)，B坐标系在A坐标系姿态为(0,0,0)，P点在A坐标系中Azp=0，则通过式(8)坐标变换后，在B为原点坐标系中的BzP仍为0，造成Δh的误差。

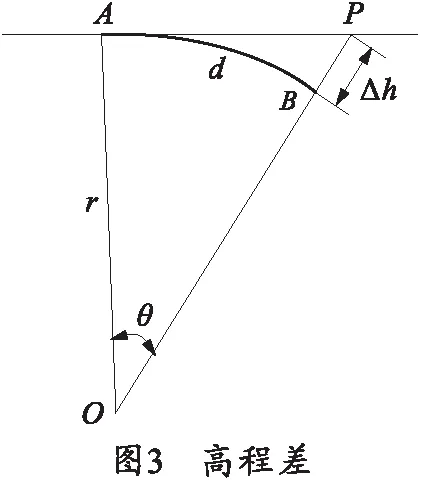
图3中O为地球的圆心，r为地球半径,d为AB两点的距离，即弧长。由图3可得：

(9)

地球半径r约为6 000 km，当d约为1 km时，Δh=0.1 m；当d约为3.5 km时，Δh=1 m；当d约为30 km时，Δh=75 m.由以上分析可以看出，当d较大时，误差已经不可忽略，实际应用中要根据精度要求来确定适用式(8)的最大距离d.当距离产生的误差不可忽略时，就要重新选取标准值坐标系和标准站心坐标系的原点。

2.3 变换到标准载体坐标系下

2.3.1 姿态定义方法

WGS-84坐标变换到标准站心坐标系后，要继续变换到标准载体坐标系中。标准载体坐标系与标准站心坐标系原点重合，只需要定义标准载体坐标系在标准站心坐标系中的姿态即可。由于测试设备的不同，常见的定义方法有两种，如图4所示。

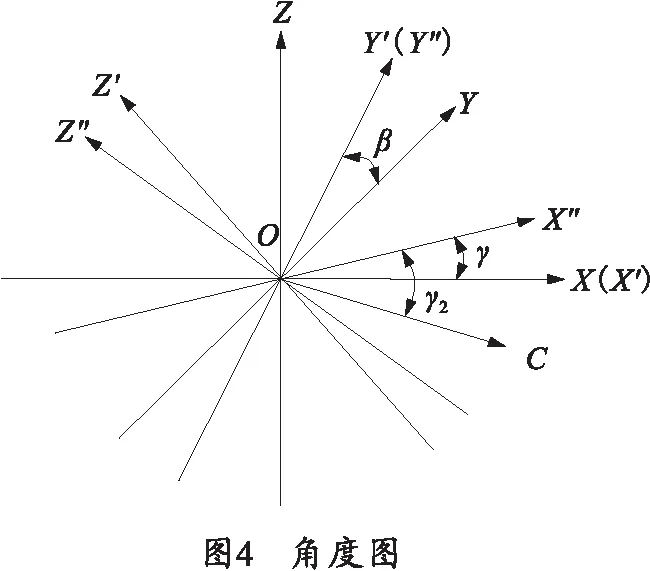
图4中O-XYZ坐标系Y轴与北向夹角为α，O-XYZ绕X轴旋转角度β得到坐标系O-X′Y′Z′，O-X′Y′Z′绕Y′轴旋转角度γ得到坐标系O-X″Y″Z″，γ2为X″轴与OXY平面的夹角。

常见的姿态定义方法一种为(α,β,γ)，即图2定义的航向角、纵摇角和横滚角，另一种方法采用(α,β,γ2)。从标准站心坐标系变换到标准载体坐标系需用到角度(α,β,γ)，如给出角度方式为(α,β,γ2)，要用式(10)进行变换：

(10)

2.3.2 变换

得到(CαV,CβV,CγV)，即可建立图1中的“站心坐标转载体坐标”方法：

(11)

最后转化为球坐标:

(12)

(14)

式(12)中VrP为距离，式(13)中VeP为高低角，式(14)中VaP为方位角。由于不同的被试品坐标定义不同，因此需要进行坐标变换。图1中“被试品坐标转载体坐标”部分用于将被试品坐标系的球坐标变化为标准载体坐标系下的球坐标。

由于被试品坐标系定义不同，变换没有通用的形式。有些产品的方位角Ta′以北为0，顺时针旋转为正，对此类产品，进行预处理：

Va′=6 000-Ta′,

(15)

距离和高低角不变。

有些产品方位角Ta′以南为0，逆时针旋转为正，对此类产品，进行预处理：

(16)

或设置航向角：

CαV=π,

(17)

距离和高低角不变。

3 统计

得到V坐标系下坐标后，用VP′-VP得到一次差。对目标指示雷达、搜索雷达用GJB 74A—1998对一次差进行统计，跟踪雷达、光电分系统用GJB 3856—1999对一次差进行统计。

经数据处理后，得到V坐标系下系统误差Vμ、均方差Vσ和均方根误差VU，可推导出与被试品坐标系下Tμ、Tσ和TU的相对关系。对于方位角逆时针旋转为正的系统，不论以南为方位0，还是以北为方位0，其方位角误差：

(18)

对于方位角顺时针旋转为正的系统，不论以南为方位0,还是以北为方位0，其方位角误差：

(19)

距离和高低角统计结果不需要进行变换。统计结束后，根据被试品坐标系对角度不同的定义方法，即可得到最终值。

4 应用

采用本文方法编写了通用于目标指示雷达、搜索雷达、跟踪雷达、红外跟踪分系统和电视跟踪分系统测量精度的数据处理程序。由于目前各侦察系统的坐标系没有统一规范，因此试验时各系统的坐标系定义并不统一，在应用程序进行数据处理时要用式(15)～(17)对程序的输入进行预处理，认为此种简单的计算不会引起浮点数计算误差。

由于统计方法不同，程序同时输出采用GJB 3856—1999和GJB 74A—1998方法进行统计得到的结果，然后根据产品类型确定选用哪种结果。

程序成功应用于某型弹炮结合防空武器系统侦察系统的竞标试验中，竞标产品包括目标指示雷达、搜索雷达、跟踪雷达、红外跟踪分系统4类13种侦察设备。

目标指示雷达有2种产品参加竞标。2种产品布站距离200 m，目标机上挂载GPS作为标准值测量设备，输出WGS-84坐标系的经纬度和大地高作为坐标。为了将误差减到最小，将WGS-84坐标用式(7)分别变换到两个竞标产品的标准站心坐标，此时标准值坐标系和标准站心坐标重合，然后再进行计算。统计了3个有效航次斜距离3～45 km航路段内距离均方根误差、高低系统误差和随机误差、方位系统误差和随机误差。

搜索雷达有2种产品竞标。2种产品布站距离150 m，采用同指示雷达同样的标准值测量方法，统计了3个航次斜距离3～18 km航路段内距离均方根误差、高低系统误差和随机误差、方位系统误差和随机误差。

跟踪雷达有2种产品竞标。跟踪雷达沿航路方向排开，试验点位间隔50 m；采用同指示雷达同样的标准值测量方法，统计了3个有效航次斜距离2～12 km航路段内距离、高低、方位的系统误差和随机误差。

光电跟踪分系统有7种产品竞标。7种产品布站在100 m范围内，采用光电经纬仪作为标准值测量工具。光电经纬仪的坐标系原点在阵地中心，由于距离较近，认为地球曲面引起的误差可以忽略，以此中心建立标准值坐标系，采用式(8)计算标准站心坐标，不需要地心坐标转标准坐标这一步骤。统计了3个有效航次斜距离2～12 km航路段内距离、高低、方位的系统误差和随机误差。

这13种产品的统计结果得到了竞标相关单位的认可，满足了竞标试验公平性的需求，写入到试验报告中。以试验报告为依据，确定了最终的中标产品。

5 结束语

笔者针对高炮侦察系统竞标试验缺乏通用的数据处理程序问题，通过建立标准坐标系，解决了不同侦察系统坐标系不同的问题；通过采用WGS-84坐标系，给出了点位距离较大时的数据处理方法。

在目标指示雷达、搜索雷达、跟踪雷达、光电跟踪分系统的竞标试验中，13种产品共用一个程序，证明了本文方法可通用于高炮侦察系统的测量精度检测，可满足竞标试验的公平性需求，亦可应用到后续高炮侦察系统测量精度试验的数据处理中。在间距200 m的指示雷达、间距150 m搜索雷达竞标试验中的成功应用，证明本文方法可解决由于布站距离大引起的地球曲面误差问题。