基于多维网络的增开列车条件下高速铁路列车运行图调整

高如虎， 牛惠民， 江雨星

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

列车运行图在确保列车运行安全的前提下，确定列车在途经各站的到发时刻，努力提高行车效率或降低运营成本，如通过能力最大化、减少总旅行时间等，并满足旅客的出行需求[1]。当客流需求出现较大波动时(如春运或节假日)，基本运行图中的开行列车不能满足高峰客流需求，就需要增开列车并调整基本运行图中的列车运行线，从而提高旅客服务质量。随着我国高速铁路网日臻完善，运输需求时变特性明显，仅靠传统的手工推线方法调整运行图，一方面难以保证列车运行图的质量，另一方面也增加了调度人员的工作负担。因此，研究增开列车条件下的列车运行图调整模型和算法至关重要。

列车运行图调整问题属于列车运行图编制(Train Timetabling Problem，TTP)范畴，是NP-hard问题[2]。从时空资源的视角看，列车运行图是各列车对有限时空资源的相互竞争、相互作用、相互影响以达到资源合理配置的结果。因此，对列车运行图的研究，本质是对铁路有限时空资源分配的组合优化问题[3]。基于此，大多文献通过建立二维时空网络或多维时空状态网络[4-6]，将原问题中各种难以求解的约束条件转换为网络中各弧段或节点的制约关系(如可达性、不相容性、网络流量守恒等)，将研究目标转换为占用网络弧段的最小费用，从而清晰地刻画复杂的列车运行图问题并将其转换为容易求解的网络最短路径问题。

一般意义上的列车运行图调整是指当列车运行状态因设备故障、恶劣天气、突发事件等影响而偏离了预定值(计划运行图)，造成列车运行紊乱时，通过重新调整列车运行线，使其尽可能恢复列车按图行车的过程。文献[7-8]构建了城市轨道交通网络中末班车时刻表调整的整数规划模型，并设计了相应的启发式算法对问题进行求解。文献[9]构建了高速铁路列车运行调整的马氏决策过程模型，并提出了极大加代数和矩阵的策略优化方法。文献[10]构建了区间突发故障下的列车运行图调整混合整数规划模型，并详细讨论了故障发生时区运行列车的停车问题。文献[11]在研究列车运行图调整时，考虑了动车组接续，并提出基于改进的和声搜索算法对模型进行求解。事实上，列车在车站的进路对于列车运行图调整至关重要，但仅有少部分文献考虑了列车运行调整时列车车站进路的安排。文献[12]将列车运行调整和列车进路选择进行协同优化，构建了基于0-1累计变量的混合整数规划模型。

本文所研究的列车运行图调整是针对当客流发生突变，需要增开列车时，如何铺画新增列车运行线并对原基本运行图进行调整的过程，并综合考虑了列车车站进路对列车运行调整的影响。为方便问题描述和模型构建，建立了基于Time-Station-Track的多维时空扩展网络，以刻画列车对铁路行车资源的占用，并将原问题转换为求解列车占用网络最少费用问题。根据问题特点，设计了拉格朗日松弛算法，将问题进一步分解为求解单列车网络最短路径子问题。

1 问题分析及说明

1.1 问题分析

对于某条高速铁路线路：U为车站集合，U={0,1,2,…,u,u+1,…,V,V+1}，其中0、V+1分别为虚拟起、终点站，1、V站分别为实际起、终点站；Pu为车站u进路集合，不同车站，进路数量不同。列车在车站的进路包括进站进路、到发线占用和出站进路，由于高速铁路车站进、出站咽喉区具有足够多的平行进路，所以列车之间在车站的作业冲突主要体现为不同列车对车站到发线资源的占用冲突。一般情况下，高速铁路上下行方向列车相互独立运行并成对开行，车站进路也分方向设置，本文仅选取线路上行方向进行研究。在该线路上：Ie为原基本运行图中计划开行列车集合；Ia为需要增开列车集合；I为所有列车集合，I=Ie∪Ia。运营时段按照1 min为粒度进行离散处理，T为优化时段中的时刻集合。

一般情况下，在调整列车运行图时，原基本运行图中列车相比新增列车具有较高的优先权，并且原基本运行图中的列车都有预先确定的列车时刻表和停站方案。当新增列车占用时空资源费用较大(旅行时间较大或出现资源占用冲突)时，可对原基本运行图的列车运行线进行局部调整。本文以在原基本运行图调整量最少的同时降低新增列车旅行时间作为优化目标。

在研究列车运行图调整时，若不考虑列车在车站的进路安排，由于车站到发线能力的限制，在列车到发密集时段可能导致列车运行图不可行。因此，在规划新增列车时，需要为新增列车安排合理的车站进路并对原基本运行图中列车的车站进路进行相应调整。

为进一步简化问题，本文作出如下假设：

假设1为尽可能减少因列车运行调整而导致的旅客乘车不便的影响，在调整原基本运行图中的列车运行线时，仅对列车始发时刻进行调整，而对停站方案及停站时间不做调整。

假设2在高速铁路线路上，当列车通过车站而不停站时，一般从正线通过，并且车站正线一般不办理列车到发作业。本文对所有车站进路进行编号，假定所有车站的1号进路为通过进路，其他进路为到发进路。

假设3在不同速度等级列车共线匹配运行模式下，为研究方便，假定高速铁路线路上仅运行高等级和低等级两类列车，且同等级列车之间不允许越行。在铁路实际运营中，应尽量减少低等级列车在车站被高等级列车连续越行的次数，本文假定低等级列车在车站最多被高等级列车连续越行2次。

1.2 变量及参数

I为列车集合；i、j为列车，i,j∈I；U为车站集合；u、v为车站，u,v∈U；Pu为车站进路集合；m、n为车站进路，m,n∈Pu；T为时刻集合；t、t′、t″、l为时刻，t,t′,t″,l∈T。

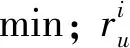
模型决策变量为

xi(u,t,m;v,l,n)=

2 网络构建

本文所建立的TST网络中包含3类弧段，下面对各类弧段的特性进行分析，并对各类弧段的费用进行定义。

2.1 弧段特性分析

(1) 起始弧

对于原基本运行图中列车，由于本文研究的是高速铁路线路，因此，基本运行图中的列车在调整时，均不能提前出发，即

对于运行图中新增列车

(2) 终止弧

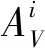
对于原基本运行图中列车，即i∈Ie

对于运行图中新增列车，即i∈Ia，由于列车停站方案不确定，因此

(3) 运行弧

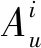
为方便说明，下面以原基本运行图中的一列车为例说明网络的构建过程，新增列车的网络与此类似。假设线路由3个车站组成，每个车站有3条进路。该列车在原基本图中的始发时刻为9 min，可调整时间为2 min，该列车在第2站不停站通过，对应在网络中仅占用通过进路(1号进路)。当列车停站时，可对其到发进路进行调整。对应TST网络见图1。

在本文所构建的TST网络中，不单独设列车停站弧，而是将停站行为包含于列车运行弧中。值得注意的是：运行弧中起点所对应的时刻为列车在该弧起点所对应车站的出发时刻，而运行弧终点所对应时刻不是该列车在该弧终点所对应车站的真实到达时刻，在后文模型建立部分中会有所体现。

2.2 弧段费用

本文以在原基本运行图中列车时刻表调整量最少的基础上，降低新增列车旅行时间作为优化目标，因此，原运行图中列车和新增列车在TST网络中占用弧段的费用不同，各类弧段费用定义见表1。值得注意的是，原运行图中列车在网络中的旅行弧和终止弧及新增列车起始弧和终止弧不影响问题优化目标，因此，为方便计算，全部设为常数1。γ为原运行图中列车时刻表调整量惩罚因子，η为新增列车旅行时间惩罚因子。

表1 弧段费用

3 模型建立

3.1 基于TST网络的0-1整数规划模型

3.1.1 目标函数

通过网络构建，将本文优化目标转化为所有列车占用弧段费用最小，即

xi(u,t,m;v,l,n)

(1)

3.1.2 约束条件

(1) 流量守恒

(2)

(2) 区间能力

出发安全间隔约束为

(3)

如前文所述，由于本文所建网络中列车占用运行弧的终止顶点对应时刻并不是列车的实际到达时刻，因此需要将其转换为真实的到达时刻。

到达安全间隔约束为

(4)

由于高速铁路线路上运行不同等级的列车，因此，需要解决不同等级列车的越行冲突，越行约束为

∀(u,t),i≠j

(5)

(3) 车站能力约束

若不同列车占用同一车站的同一进路，则必须满足最小安全间隔

(6)

(4) 变量约束

xi(u,t,m;v,l,n)∈{0,1}

(7)

3.2 Lagrangian松弛及问题分解

列车运行图优化模型中，通常认为制约模型求解效率的难约束是能力约束。对于本文所建立模型，区间能力和车站能力约束式(3)—式(6)导致列车之间相互作用、相互影响，从而发生大规模的组合。因此，通过引入拉格朗日乘子将此类难约束作为惩罚项松弛到目标函数中，形成拉格朗日松弛问题。本文引入ρu,t、φi,u,t、πu,t,m3类非负拉格朗日乘子。

拉格朗日松弛问题为

(8)

通过转换，可将上式重新整理为

(9)

式中：Ω为关于拉格朗日乘子的常数。

(10)

为获得拉格朗日松弛问题的最大下界，需求解以下拉格朗日对偶问题

(11)

s.t. 式(2)、式(7)。

其中

LRi=

(12)

利用次梯度法对拉格朗日乘子进行更新，如对乘子ρu,t更新为

(13)

式中：q为迭代次数；αq为第q次迭代的歩长。

αq更新公式为

αq=1/(1+q)

(14)

其他乘子更新方法同ρu,t。

根据式(11)和式(12)，显然，原问题被分解成求解单列车的网络最短路径问题。通过拉格朗日算法不断迭代可求解原问题的解。值得说明的是，拉格朗日松弛算法的对偶解可能不可行，因此，本文利用基于列车优先序列的启发式调整方法对对偶解可行化，基本思想类似于文献[12-14]。拉格朗日松弛算法框架如下：

Step1初始化。令q=1，上界UB0=+，下界LB0=-。初始化拉格朗日乘子值ρu,t，φi,u,t，πu,t,m。

Step2下界计算。利用Dijkstra最短路算法依次求解各个列车在Time-Station-Track网络中的最短路径；并计算下界LBq，更新LBq=max{LBq,LBq-1}。

Step3基于列车优先序列的上界计算。

(1) 确定列车可行顺序：首先，将列车按照式(10)的计算结果从大到小进行排序；然后，再按照原基本运行图中列车在前，新增列车在后的顺序排序。

(2) 计算最短路并标定：根据(1)列车可行顺序，利用Dijkstra最短路算法计算各个列车在TST网络中的最短路径，标定该列车最短路占用TST网络弧段，并令该列车占用弧段的费用为+。

(3) 可行解判定：若所有列车全部规划完毕，则转(4)；若存在列车不能被规划，则改变规划失败列车的优先权，优先规划前次失败的列车，转(2)。

(4) 计算上界UBq并更新UBq=min{UBq,UBq-1}。

Step4拉格朗日乘子更新。按照式(13)，利用次梯度方法对各类乘子进行更新。

Step5gap值计算。gap=(UBq-LBq)/UBq。

Step6终止条件判断。若gap≤ε或者q≥M，算法停止，输出；否则q=q+1 ，转Step2。其中，ε、M分别为预先确定的预期gap值及最大迭代次数。

4 算例

新增低等级列车的最大停站时间示意见图3。

表2 区间运行时间 min

表3 原运行图中高等级列车在始发站的原出发时刻和停站方案

表4 新增低等级列车最早最晚出发时刻

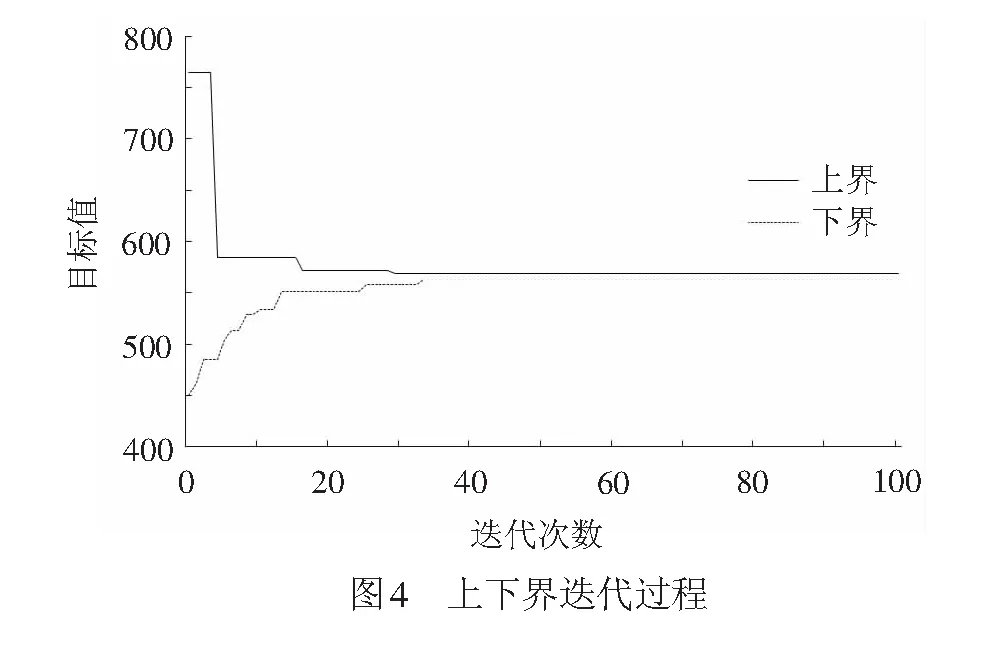
对实例利用Lagrangian松弛算法求解，算法在Visual Studio 2013平台上使用C++语言实现，算法运行环境为1台CPU Intel，4 GB内存的个人计算机。算法迭代100次，运行时间3 862 s，gap值为1.05%。

上下界迭代过程见图4，从算法迭代过程及gap值可以看出，该算法具有较好的收敛性。优化后的列车运行图见图5，由于篇幅限制，各列车占用车站进路不再展示。

由于本文原问题目标为在基本运行图中列车时刻表调整最小的基础上，减少新增列车的旅行时间。在建立的TST网络中表现为两类列车占用弧段费用不同，即γ>η，其内涵为基本运行图中列车占用TST网络时空资源费用高于新增列车。事实上，两惩罚参数对拉格朗日松弛算法的迭代次数有影响，而对最终求解结果影响不大，经过反复对参数进行测试，γ=1，η=2时，算法的收敛效果最好。从计算结果分析可知，一般对基本运行图中列车时刻表不做调整，仅当车站资源占用出现冲突时，可通过调整列车再车站的进路或者调整列车在始发站的出发时刻，如列车编号27、28、34。对于新增的低等级列车，虽然优化目标中降低其旅行时间，但由于线路能力限制，在车站需要待避原基本运行图中高等级列车，导致停站次数较多，停站时间也较长。

5 结论

(1) 列车运行图问题属于典型的NP-hard问题，并且列车运行图问题所涉及车站和列车数量众多。本文对新增列车条件下的列车运行图调整进行了研究，并综合考虑了列车车站进路选择。

(2) 本文通过构建TST三维时空扩展网络将列车运行调整问题转换为求解列车在TST时空扩展网络中占用弧段的最小费用问题，并利用拉格朗日松弛算法，将原问题进一步分解为单列车网络最短路径子问题。由于利用拉格朗日松弛算法将原问题分解后，得到的解可能是不可行解，因此，设计了基于列车优先序列的启发式算法求原问题的可行解并获得拉格朗日松弛算法的上界。

(3) 通过实例验证了本文所建立模型的正确性和所设计算法的适用性。下一步将考虑面向时变客流需求条件下的高速铁路列车运行调整问题，并将提出更加高效的算法对此类复杂的组合优化问题进行求解。