基于电机定子电流分析的机车齿轮箱故障诊断
2020-05-29杨江天薛灿灿岳建海
张 璋, 杨江天, 薛灿灿, 岳建海
(北京交通大学 机械与电子控制工程学院,北京 100044)
齿轮箱是机车走行部的关键部件,重载运输和高速运行对机车齿轮的性能提出了更高的要求。机车线路运行时载荷复杂多变,工作条件恶劣,很容易引发齿轮故障。因此,先进的齿轮工况检测与故障诊断装置对机车保障牵引传动系统可靠运转和列车行车安全有重要意义[1-2]。
常规的机车齿轮故障诊断多采用基于振动信号分析的方法[3-4]。工程实践表明基于振动信号分析能有效诊断机车齿轮故障,但也存在以下缺点[5-6]:①布置振动传感器需要增加费用,且机车(动车组)传动结构紧凑,有的车型没有合适的位置安装传感器;②振动传感器易受到外部干扰,必须仔细维护防止误报警发生;③机车运行环境对振动测量结果影响很大,振动信号复杂,功率谱图上有时某些重要的频率成分缺失,影响诊断的准确性。
电机定子电流特征分析是异步电机电气与机械故障检测行之有效的方法[7]。异步电机是一个高度对称的电磁系统,因此任何电机故障都会导致一定程度的不对称,不对称引发气隙中旋转电磁场变化,在定子电流中感应出新的频率分量。定子电流特征分析正是通过检测某些特征频率分量幅值的变化实现故障诊断的。工业应用中,由于系统保护的要求,通常已经安装电流互感器检测电机电流。因此定子电流分析诊断法不需要额外增加传感器,其非接触测量和容易实施的优点使其广泛用于诊断各种类型的电机故障[7-10]。
机械传动系统中齿轮箱通常和驱动电机耦合在一起,当齿轮出现故障时,扭转振动发生变化,产生转矩波动。为了平衡附加的转矩,电机将产生一个相应的电转矩,引起定子电流频谱出现轻微的幅度调制。分析电机定子电流信号调制可以诊断齿轮故障[10-11]。扭振在定子电流中映射非常微弱,调制生成的频率分量被高幅值的信号(如电机供电频率及其谐波)和噪声所遮掩。此外齿轮损伤到电机定子电流复杂的传递路径,也使得故障信号的信噪比很低,故障特征提取必须用先进的信号分析方法[10-12]。
小波分析相当于数学显微镜,能从粗到精、从远及近地逐步观察信号,获得较好的频率分辨率,适用于电机定子电流分析[6-8,13]。但是传统小波变换小波系数剧烈震荡,存在平移敏感性和频带混叠现象。双树复小波变换[14]在保持经典小波变换时频局部分析能力的同时,因为具有近似平移不变性和抗频率混叠性,从而能获得更高的频率分辨率[15-16]。熵是对能量分布有序性的描述,Blanco等[17]基于小波变换提出了小波能量熵,描述信号能量分布特性和紊乱程度。小波能量熵对信号中异常成分引起的能量分布变化敏感,因而被用来检测信号中异常成分,监测机械运行状况。
本文将双树复小波变换引入机车牵引电机定子电流分析,提出将电流信号小波能量熵作为特征量监测故障,进而分析小波节点特征频率判断故障类型的齿轮故障诊断方法。试验证明该方法能有效诊断各种类型的机车齿轮箱故障。
1 电机定子电流中齿轮故障特征频率
齿轮局部故障导致机械扭矩变化,会引发传动系统产生以旋转频率为周期的剧烈振动,映射到驱动电机定子电流中[11-12]。有关研究表明,正常工况条件下,齿轮箱驱动电机上观测到的负载扭矩可分为静扭矩和动扭矩,即
TLH(t)=T0+Tosc(t)
(1)
式中:t为采样时间;TLH(t)为负载扭矩随时间的变化;T0为静扭矩(平均扭矩);Tosc(t)为齿轮啮合刚度变化和传动误差引起的动扭矩。
当齿轮发生故障时,会产成一个附加的周期成分。因此故障时负载扭矩TLF(t)为
TLF(t)=TLH(t)+Tfp(t)
(2)
式中:Tfp(t)是由齿轮局部故障引起的零均值周期性成分,可用傅里叶级数表示为
(3)
其中,ffp为故障齿廓的基频,对于一级齿轮系统,基频与大小齿轮旋转频率有关;k取整数,Tk和φk可由故障齿廓傅里叶级数系数获取。
因此,驱动电机定子电流可以表示为
IA(t)≈Issin(ωst)+
Irsin(ωst+χLH(t)+χfp(t)+ηr)
(4)
式中:ωs=2πfs为供电频率;ηr为与相位调制有关的相角;χLH(t),χfp(t)分别为与正常和故障齿廓有关的相位调制分量。
故障条件下相位调制分量χfp(t)定义为
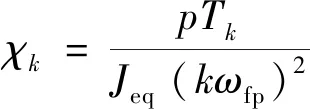
(5)
式中:αk为与χfp(t)相对应的相角;Jeq为感应电机的等效转动惯量;p为电机的极对数。
考虑到χLH(t)、χfp(t)的幅值很小,当x远小于1时sin(x)≈x,cos(x)≈1。这样,式(4)中的定子电流表达式可化简为
IA(t)≈Ihealthy(t)+Ircos(ωst+ηr)χfp(t)
(6)
式中:
Ihealthy(t)≈Issin(ωst)+Irsin(ωst+ηr)χfp(t)+
Ircos(ωst+ηr)χLH(t)
(7)
利用式(5)可重写电机定子电流表达式为
IA(t)=Ihealthy(t)+
(8)
式中:φl,k=ηr-αk,φr,k=ηr+αk。
因此,定子电流中的故障频率可以表示为
ffaulty=|fs±mffp|
(9)
式中:m= 1,2,3,… 。
以上分析表明,机车齿轮发生局部故障时,牵引电机定子电流信号中出现一些新的频率成分,在供电频率两侧形成边频带。这些频率成分非常微弱,需要用高分辨率的信号处理方法才能有效识别。
2 双树复小波变换
小波变换广泛用于电机定子电流分析,提取特征频率。常规小波具有平移敏感性、方向性差、缺乏相位信息的缺点,分解过程中易发生频率混叠产生虚假频率,有时使用效果不够理想。
如果小波基函数是复函数,小波变换后得到的小波系数也是复数,则为复小波变换。相比于实小波,复小波变换能较好地克服平移敏感性、方向性差、无相位信息等缺点。
双树复小波变换(Dual Tree Complex Wavelet Transform)是基于实数小波变换实现的复小波变换,由2个相互平行而使用不同高通和低通滤波器的离散小波变换构成,双树小波滤波器满足半采样延迟条件,即始终保持虚部树的采样位置位于实部树的中间,从而有效地综合利用了采样前小波变换系数,实现双树信息互补。因此能获得近似平移不变性,有效抑制频率混叠。用双树复小波分析电机定子电流信号可以获得更高的频率分辨率,准确提取故障信息,下面通过仿真信号分析来说明。考虑以下信号
i(t)=3cos(2πft)+
[0.8cos(6πft)+0.6cos(14πft)+
0.3cos(22πft)+0.15cos(34πft)+
0.11cos(38πft)]×
[1+0.03sin(16πt)]+
0.1cos[2π(1±2s)ft]+e(t)
(10)
式中:f= 50 Hz为电源供电频率,受到3、7、11、17、19次谐波信号“污染”;s=2%为电机转差率。与之对应,供电频率两侧存在48 Hz和52 Hz的边频带结构;e(t)为功率为1的均匀分布的白噪声,模拟噪声干扰。
信号i(t)及其小波分解见图1。其中图1(a)为i(t)的功率谱,采样频率为2 000 Hz,采样点数为4 096。在功率谱中可以看到供电频率及其谐波成分,但是无法找到48 Hz和52 Hz边频带。
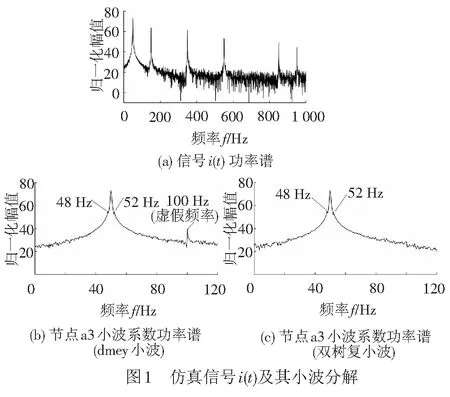
对信号i(t)进行小波变换3层分解,小波基函数选用电机定子电流信号分析常用的dmey小波。图1(b)为3层小波分解后节点a3小波系数功率谱,对应的频带0~125 Hz。在图1(b)中可以找到50 Hz的供电基频及两侧边频带。但是由于频率混叠,功率谱图上还出现了100 Hz虚假频率成分。
图1(c)为信号i(t)双树复小波3层分解a3小波系数功率谱。50 Hz供电基频及两侧48、52 Hz边频带结构清晰,且无任何虚假频率分量。相比于传统小波,双树复小波分析电机定子电流信号,能获得更高频率分辨率,有效提取故障特征。
信号x(t)经双树复小波I层分解,得到I+1个子带信号,每个子带信号能量Ei为
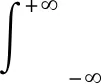
(11)
式中:i=1,2,…,I,I+1;Wf(i)为双树复小波变换后得到的小波系数。
根据香农熵定义,双树复小波能量熵WEE为
(12)
小波能量熵越大,说明频域能量分布越均匀,信号的复杂度越大。下面用仿真信号说明电流信号小波能量熵可以作为特征量监测故障。
考虑以下信号
i1(t)=cos(2πft)+0.1cos[2π(1-2s)ft]+
0.1cos[2π(1+2s)ft]+e(t)+
(13)
式中:f=50 Hz为电源供电频率;fr=12 Hz模拟故障齿轮的旋转频率。供电频率谐波两侧存在间隔为fr的边频带,模拟故障特征频率;A为故障特征频率幅值,反映不同的故障程度。
计算不同故障程度下的双树复小波能量熵和正常状态下(A=0)双树复小波能量熵对比,结果见表1。可以看出:当故障程度增加时,小波能量熵单调增长,涨幅有效值明显。正常状态时,电机定子电流信号的频率成份少,能量集中在低频段;发生故障后,产生新的频率成份,信号变复杂,小波能量熵增大。
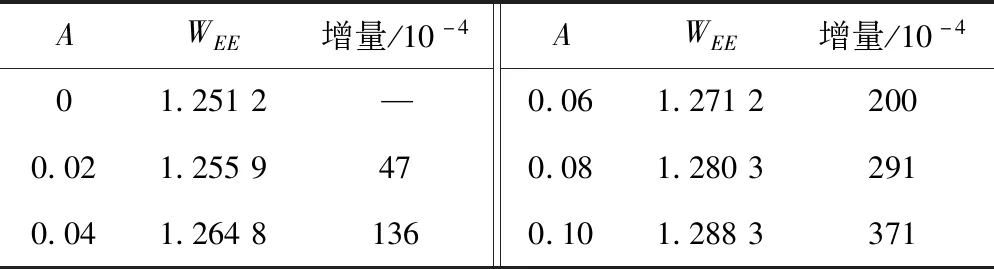
表1 不同故障程度下双树复小波能量熵和增量
3 实验验证
模拟机车(动车)一根轴的传动实验台见图2。变频器将220 V单相交流电转换为三相电,驱动实验电机(牵引电机)旋转,齿轮箱减速后,驱动车轴转动。车轮带动轨道轮旋转,经齿轮箱增速,驱动直流发电机发电,电阻箱将电能转换成热能,耗散在空气中,模拟载荷。实验齿轮箱传动比为28∶85,实验电机额定转速2 865 r/min。安装互感器观测牵引电机三相供电中两相的电流。

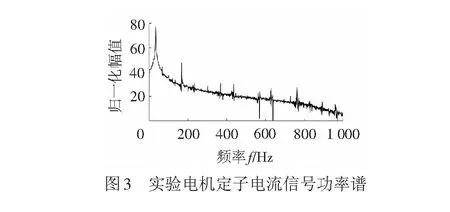
实验电机(牵引电机)采用YX3-90S-2型三相异步电动机,额定功率1.5 kW、电压380 V、电流3.3 A、供电频率50 Hz,极数为2。正常状态下,电机三相供电中的a相定子电流功率谱见图3,采样频率2 000 Hz。实验时电机供电频率34 Hz,对应转速2 000 r/min。小齿轮旋转频率f1=33.33 Hz,大齿轮旋转频率f2=10.98 Hz,齿轮啮合频率fmesh=933 Hz。
对采集到的定子电流信号进行双树复小波三层分解,分解结果见图4。图4中可见供电频率及谐波成分和变频带。由于电机结构和运行环境的影响,边频带存在不对称现象。换装齿面磨损、齿根裂纹和断齿的大齿轮与小齿轮,采集定子电流信号,进行双树复小波三层分解,计算双树复小波能量熵,结果见表2。当齿轮发生各种故障时,小波能量熵都比正常值有所增加。双树复小波能量熵可以作为特征量监测齿轮故障,判断故障类型需要进一步分析。
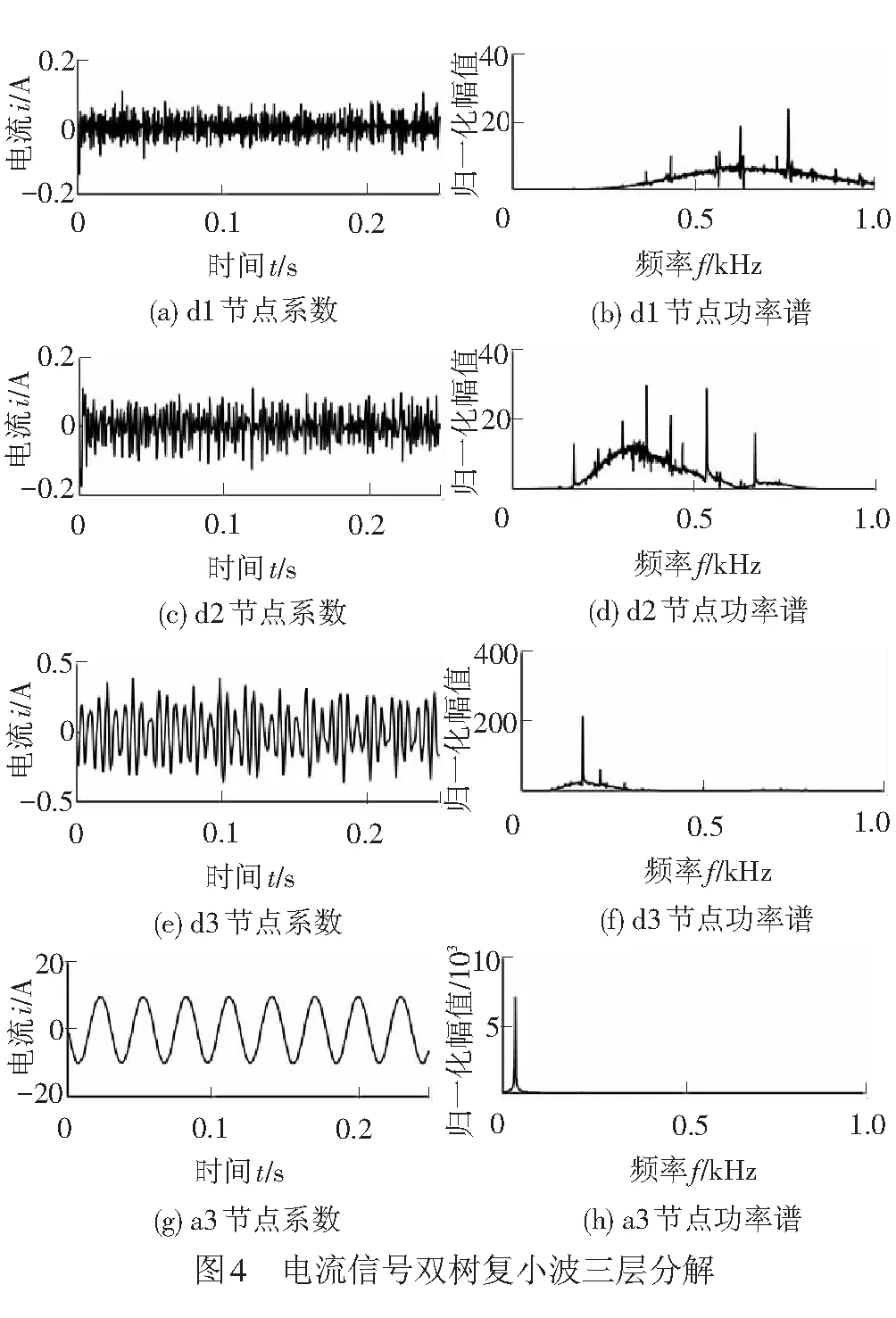
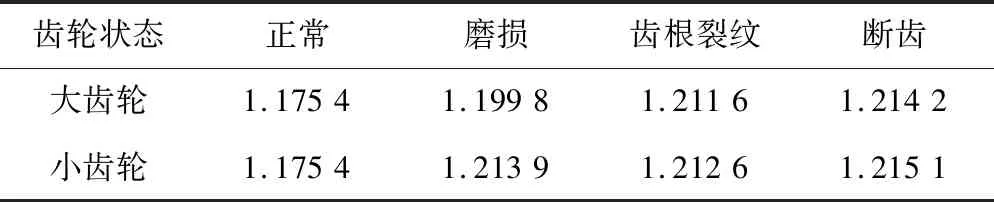
表2 大小齿轮4种工况下双树复小波能量熵
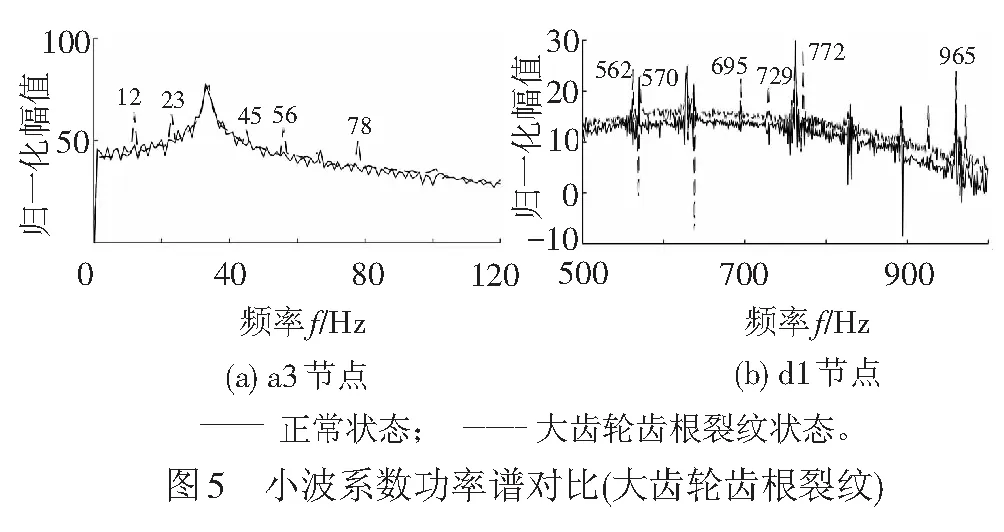
研究分析大齿轮齿根裂纹状况下电流信号小波系数功率谱。为了方便对比,将a3和d1 2个节点的功率谱与正常状态下电流信号小波分解后对应节点小波系数的功率谱绘制在同一张图上,见图5。由图5可以看出,在a3节点的功率谱中,12、23、45、56、78 Hz频率分量的幅值明显增加,对应式(9)中m分别取-2、-1、1、2、4。而在d1节点的功率谱中,562、695、729、772 Hz频率分量的幅值增加,对应m取48、60、63、67。此外,功率谱中可以找到570 Hz频率分量(为供电频率17次谐波)和 965 Hz谱峰(对应fs+fmesh,为啮合频率在定子电流中的映射)。上述分析表明,大齿轮齿根裂纹故障使得电机定子电流信号中与大齿轮故障相关的特征频率幅值增加。
下面对比分析小齿轮磨损工况与正常工况条件下电机定子电流信号。将2种工况下a3和d2节点小波系数功率谱绘制在同一张图上,见图6。
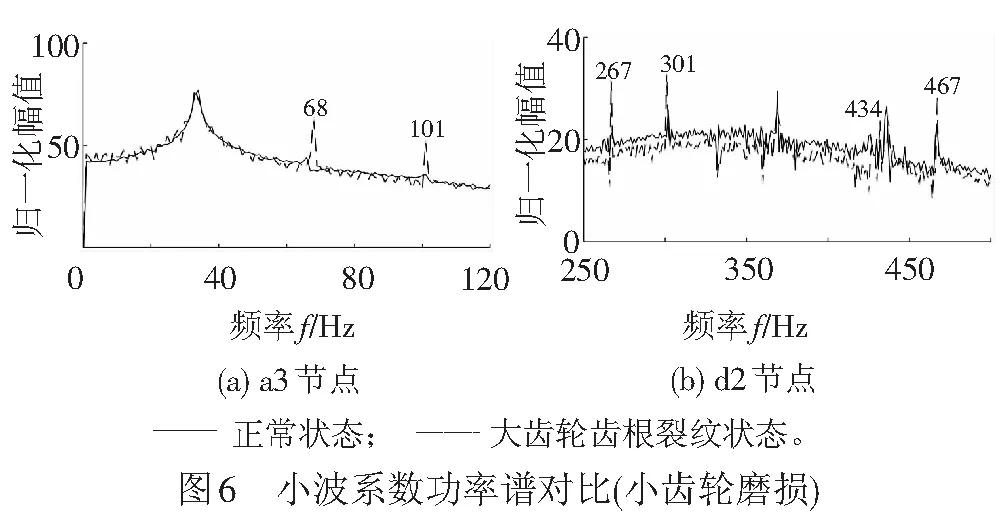
对比发现,在a3节点的图谱中,68、101 Hz频率成分的幅值有了明显的增加,对应式(9)中m取1、2。在节点d2的功率谱中,267、301、434、467 Hz频率成分的幅值明显增加,对应m取7、8、12、13。当小齿轮发生故障时,电机定子电流频谱中与小齿轮故障有关的特征频率幅值增加。
实验表明:当齿轮发生故障时,故障特征频率会映射到电机定子电流中。检测分析定子电流信号频谱,能有效诊断齿轮故障。
4 工程应用
在仿真信号分析和实验台实验基础上,将本文提出的方法用于机车运行试验,在工业现场验证其有效性。
4.1 诊断实例一
为适应国家铁路重载运输发展需要,大同电力机车有限公司研制了30 t轴重交流传动货运机车。该机车8轴驱动,总功率9 600 kW,最高时速100 km,用于瓦日铁路运输。机车采用YJ245A牵引电机,额定功率1 226 kW,额定电压1 391 V,额定电流590 A。齿轮箱传动比为19∶108。
机车使用前后牵引电机定子电流信号对比见图7。图7(a)为机车刚投入试验时,某牵引电机a相定子电流功率谱。机车运行速度98 km/h,供电频率为78.5 Hz,小齿轮的旋转频率f1为39.42 Hz,大齿轮的旋转频率f2为6.94 Hz,啮合频率fmesh为749 Hz。
图7(b)为机车试验运行6个月后,在同样运行速度(98 km/h)下采集到的电机定子电流信号的功率谱。
从图7中可以看出,由于电机结构和噪声的作用,定子电流中存在诸多谐波分量。供电频率及其谐波两侧存在边频带结构。图7(a)、图7(b)差别不大,功率谱分析频率分辨率不够高,仅根据电机定子电流信号功率谱难以诊断机车传动系统故障。

对采集到的牵引电机定子电流信号进行双树复小波三层分解。参照以前用的方法,将2次试验结果画到一张图上,a3与d1节点小波系数功率谱对比见图8。在图8(a)中,可以找到39 Hz和118 Hz 2个幅值明显增加的频率成分;而在图8(b)中,631 Hz的频率成分幅值显著增加。根据式(9),以上频率为机车齿轮箱小齿轮故障特征频率。
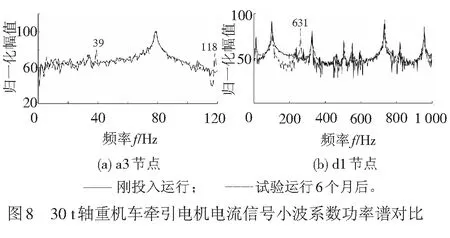
由此判断,机车传动系统小齿轮磨损。经解体检修,证实了诊断结论。
4.2 诊断实例二
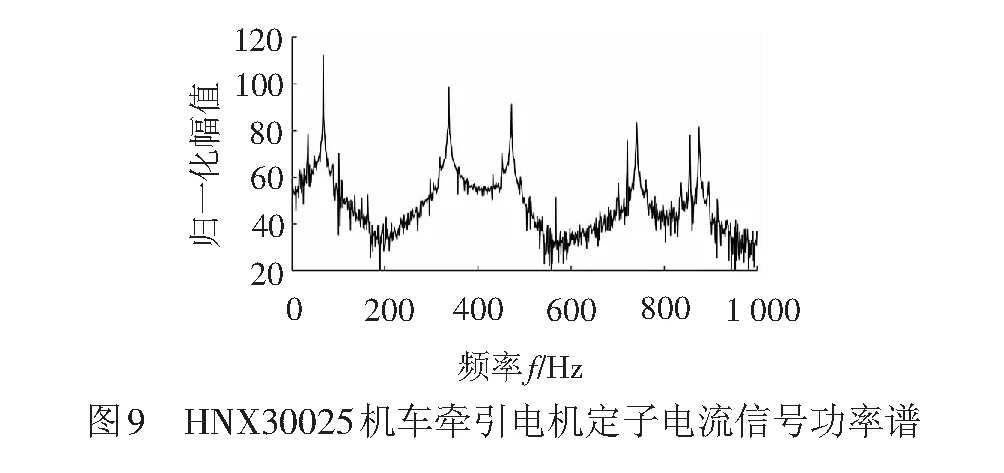
HXN3型交流传动内燃机车采用 6 台YJ116A型牵引电机,额定功率663 kW,额定电流219 A,传动比16∶85。主要用于某局西部铁路干线货运。一次行车中,发现HNX30025机车的1位转向架存在异音。检测各牵引电机定子电流信号,3号牵引电机b相电流信号功率谱见图9。采样时机车运行速度 77 km/h,对应电机转速 2 076 r/min,供电频率为 67.4 Hz,小齿轮转频f1=34.6 Hz,大齿轮转频f2=6.5 Hz,啮合频率fmesh为553 Hz。
对定子电流信号进行双树复小波三层分解,a3与d1节点小波系数功率谱见图10。在图10(a)中,供电频率67.4、34.2 、86.9、100.6 Hz 谱线清晰可辨;图10(b)中可以找到740、875 Hz供电频率谐波和567.4、663.1、720.7、855.5 Hz频率成份。根据式(9),34.2、86.9 、100.6 Hz为齿轮箱大齿轮故障的特征频率;567.4、663.1、720.7 、855.5 Hz为与大齿轮旋转频率和啮合频率相关的特征频率。
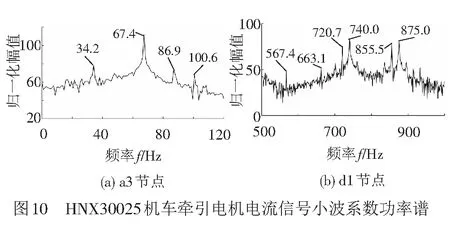
依此判断该传动轴大齿轮故障。检修时发现大齿轮出现齿根裂纹,证实了诊断结论。基于电机定子电流双树复小波分析的机车齿轮箱故障诊断方法获得了成功。
5 结论
本文将双树复小波变换引入定子电流分析,诊断机车的齿轮故障,并得到了以下结论:
当齿轮出现故障时,机械扭矩会发生变化,引发驱动电机定子电流产生相位调制,导致定子电流频谱出现边频带。齿轮故障引发的边频带非常微弱,完全淹没在高幅值的谐波频率成份和噪声之中。
双树复小波能量熵描述频域能量紊乱程度,可作为诊断指标检测齿轮故障。双树复小波分解能获得较高的频率分辨率,检测各节点小波系数的功率谱,识别故障特征频率,能准确诊断齿轮故障类型。
基于电机定子电流信号分析的机车齿轮箱故障诊断方法具有经济和容易实施的突出优点,受车体与转向架振动、轨道激励等因素的影响小。线路运行试验证明,采用定子电流分析法可以有效诊断各种机车齿轮故障。
