一种动车组转向架装配线电机传动系统健康状态评估优化方法研究

张 宁, 刘 锐,2

(1.北京交通大学 计算机与信息技术学院，北京 100044;2.国网山东省电力公司 德州供电公司，山东 德州 253011)

在动车组自动化装配线的各个关键组件中，电机传动系统是最为核心的，但同样也是最易发生故障的，因此电机传动系统的健康状态评估对于提高整条生产线的可靠性与工作精度、提升生产效率具有重大意义。随着设备的维修费用在全生命周期费用中所占的比重越来越大，“经济可承受性”成为企业日益关注的问题。

传统的“事后维修”和“计划维修”不仅效率低下，还易造成资源浪费，很难满足现代智能制造大趋势下的设备运维检修需求，因此基于设备的“状态修”是“可靠性维修”[1]的重要组成部分，其根据设备的实时运行数据进行状态评价与风险评估，已经成为一种更为合理的检修策略。

在设备维修的早期阶段，工程人员使用“故障”与“正常”的二值形态来描述设备的工作状态，随着相关技术的不发展，人们发现只用二值函数来定义设备状态是不完全的，于是便引进了生物学领域中的“健康状态”一词，将复杂系统的工作状态进行多级划分，这就是设备的“多值状态”。健康状态评估在整个故障预测与健康管理[2]领域中占有非常重要的地位，是PHM系统的核心功能之一。

传统的健康评估方法主要有2种，基于信号分析与基于模型分析。信号分析的典型文献如文献[3]中的定子电流法(MCSA)和文献[4]中的负载转矩分析法(LTSA)，都是应用快速傅里叶变换(FFT)进行频谱分析，以此进行健康评估。文献[5] 是将电机学原理、控制理论与数学建模三者相结合，通过建立多阶微分方程对电机模型进行线性化设计，从而对电机传动系统进行综合的健康状态评测。

无论是基于信号处理还是基于数学建模的状态评估方法，都需要有丰富的专家知识、精确的数学模型和大量的标签化数据，然而，这些条件对于装配线上的电机传动系统来说是难以获取的。本文将整个电机传动系统看成一个黑匣子，采用数据驱动的方法，利用实际电机传动系统运行中较易采集的数据，即电机的电流、电压、转速，对这三类数据进行K-Means聚类，提出基于局部异常因子算法去除噪声点，以及通过计算样本区域密度选取初始中心点，对K-Means算法进行优化。根据聚类结果，可对实际运行中的电机传动系统健康状态评估，该算法具有广泛应用价值。

1 K-Means聚类算法

聚类分析[6]是数据挖掘领域的一个重要分支，是一种无监督的学习方式，相较于监督式学习，聚类算法最大的特征就是无标签式学习，算法仅仅通过对数据相似程度的计算，将数据分为若干各类。K-Means算法[7]就是一种最为典型的聚类算法，其算法描述如下：

Step1随机选择k个对象作为初始簇中心。

Step2计算每个数据对象与聚类中心的距离，根据计算出的距离，将对象赋给“相似”的簇。

Step3通过计算簇的平均值更新簇中心。

Step4迭代Step2与Step3，直至簇中心不再发生变化。

K-Means算法收敛速度快，简单易实现，而且在处理大数据集时可保持较好的伸缩性与高效性。但是传统K-Means算法存在3个缺点[8]：①难以选定最佳K值；②K-Means初始化聚类中心时，初始点选取的随机性与不确定性，很容易使聚类结果不稳定甚至陷入局部极小值；③原始样本数据中存在的异常数据会影响K-Means算法的收敛，导致聚类结果出现偏差。

针对K-Means算法的改进，文献[9]中提出了最大最小距离的算法，选择相互距离最远的k个数据对象作为初始聚类中心；文献[10]将改进后的差分进化算法和K-Means算法相结合，进行初始中心点优化；文献[11] 提出了一种结合关系矩阵和图论的分析方法，从而确定K-Means算法的k个初始中心点。此外，通过K-Means算法还衍生出了诸如K-Means++、K-Medoids、模糊K-Means等聚类算法；文献[12] 采用遗传算法求解初始质心及遗传算法用于改进K-Means算法；文献[13] 提出了一种基于减数聚类的局部敏感K-Means聚类算法，最初的中心是由减数聚类产生的，而不是随机的。但上述研究中，主要的关注点在聚类中心点的选取，对于数据样本中的离群点与噪声点过于敏感问题，还没有很好的方法，算法的验证多是基于UCI数据库的测试数据集，而对于实际工程中数据的算法应用较少。

2 K-Means算法优化

2.1 LOF算法优化K-Means

针对样本数据中的异常数据会影响K-Means聚类结果[14]，本文采用LOF算法进行优化，算法描述如下：

Step1设样本空间为Ω，计算样本中每个对象p与其他对象o(p,o∈Ω)的欧氏距离d(p,o)。

Step2计算对于点p的第k距离dk(p)，即dk(p)=d(p,ok)。计算方法为：计算点p与集合中其他点oi之间的距离d(p,oi)，对所有距离按照升序排序并组成序列[d(p,o1),d(p,o2),…,d(p,on)]，找到序列中的第k个值d(p,ok)，其对应的就是第k距离；定义点p的第k邻域为NK(p)，表示p的第k距离以内的所有点。

Step3计算点o到点p的第k可达距离re_disk(p,o)，如果点o位于NK(p)内，则第k可达距离为k-dis(p,o)；否则，为d(p,o)。其式为

re_disk(p,o)=max{k-dis(p,o),d(p,o)}

(1)

Step4计算点p的可达密度loc_re_dek(p)，表示NK(p)中各个点到点p的平均可达距离的倒数。其式为

(2)

可达密度越高，越可能属于同一类；可达密度越低，越可能是异常点[15]。

Step5计算局部离群因子loc_ou_fak(p)，表示为邻域点Nk(p)的局部可达密度loc_re_dek(o)与点p的局部可达密度loc_re_dek(p)之比的平均数，其式为

loc_ou_fak(p)=

(3)

局部离群因子的值接近1，表明p与其邻域点Nk(p)越有可能属于同一类；大于1，表明p点越可能是异常点，因为p的密度远小于其邻域点密度；同理，小于1，表明p越可能为密集点，因为p的密度远高于其邻域点密度。

2.2 计算样本密度选取初始中心点

针对K-Means在初始聚类中心点的选取方式上过于随机化的缺陷，本文通过计算样本密度选取初始中心点，具体算法为:

① 定义样本点x的区域密度des(x)为以x为球心，λ为半径所形成的球体内的样本个数，其式为

des(x)={p|dis(x,p)≤λ,p∈Ω,x∈Ω}

(4)

(5)

其中，k为聚类个数。

遍历原始样本中每一个点xi以λ为半径所形成区域内的样本点数目。定义属性ξi为峰值间距，表示任意2个簇中心的欧氏距离，则对于样本点xi，其最短峰值间距计算程序为

Forj=1,2,3,…,n

if(des(xj)>des(xi))

ξij=‖xi-xj‖2

elseξij≈+

ξi=min{ξi1,ξi2,…,ξin}

End for

则对于每一个样本点，都对应2个属性样本点区域密度见表1。

表1 样本点区域密度表

按照最短峰值间距进行降序排序，则前k个最短峰值间距对应的样本点即为初始k的簇中心点。

② 最短峰值间距中获取的每个中心点都对应一个类，计算每个中心点到样本中所有点的距离(可根据实际应用需求选择不同的距离公式，如欧氏距离、马氏距离等)，并将每个点放入与中心点距离最短的那个类中。

③ 重新选取新的中心点。计算规则是在②生成的类中，计算任意一点与类内其他样本点的方差，选取最小值。

④ 重复②与③，直至样本中心点不在发生变化，则最终聚类结束。

2.3 聚类评价指标

CP指数用于评价聚类结果中各个类的紧密程度，计算式为

(6)

式中：CP为类内各点到聚类中心点的平均距离，CP越低，意味着类内聚类距离越近，类内越紧密;Ωi为第i类样本点集；count|Ωi|为第i类中的样本点个数；x为第i类的样本点；wi为i类的类中心。

SP指数用于评价聚类结果类间的分离度，计算式为

(7)

式中：SP为聚类中心点两两之间的最小距离，SP越高，说明类间距离越远。

DB指数[16]表示任意类中的样本点到中心点的距离均值CP除以该类与其他任意类的最小中心距离SP。DB指数越小说明类内间距越近，类间距离越远，聚类质量越好。

SC指数[17]是聚类结果评价的重要参数之一。他既集合了对聚类结果凝聚度与分离度的评价，又可以体现出聚类初始个数K对于聚类结果的影响。其计算过程为:

Step1计算第i个元素xi与其同一簇内所有其他元素距离的平均值avg_i，用于量化簇内凝聚度。

Step2选取xi外的一个簇Λ，计算xi与Λ中所有点的平均距离lat_i，并且遍历其他簇，求出最小的平均距离，用于量化簇间分离度。

Step3通过SC_xi=(l_i-avgi)/max(l_i,avgi)计算轮廓系数。

Step4计算所有x的轮廓系数，求出平均值作为当前聚类的轮廓系数。

3 实验结果与分析

3.1 电机传动系统原始数据

本文数据集基于某动车组转向架装配线中实际运行的工程数据，数据集仅有3个属性，分别为电流、电压、转速，见表2(仅展示部分数据)。本文使用Matlab对电机传动系统的原始数据进行三维展示，见图1。

表2 部分数据信息

3.2 聚类对比分析

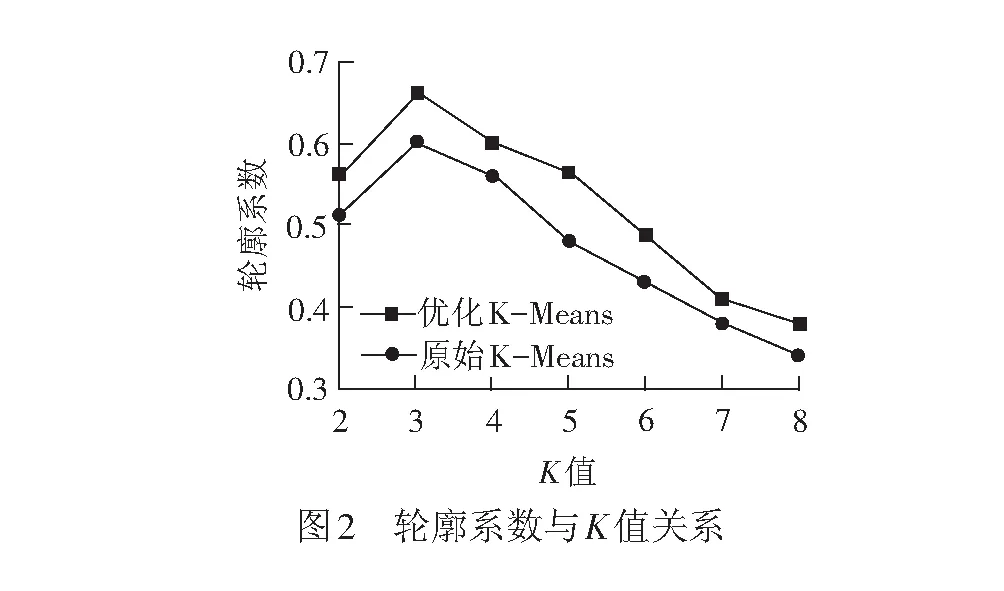
原始数据杂乱无章，现利用优化后的K-Means算法进行数据聚类，挖掘出数据中的潜在规律。通过对实际电机传动系统数据进行聚类，采取枚举法计算轮廓系数，以选择最佳K值。轮廓系数与K值的关系图见图2。由图2可见，K=3时，数据聚类的轮廓系数最好，说明对于实际的电机传动系统运行数据，聚成3类是最好的选择。

原始K-Means算法与优化后的K-Means算法实现的聚类结果见图3，由图3可以看出，优化后的K-Means使得聚类结果更加合理。

原始K-Means算法与优化后的K-Means算法3个聚类的DB指数对比见图4。从图4和图2可见：相较于原始K-Means，优化后的K-Means算法类内距离变得更小，类间距离变得更大，优化效果显著。

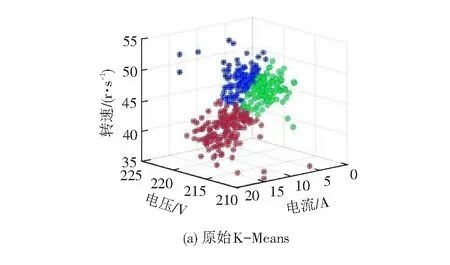
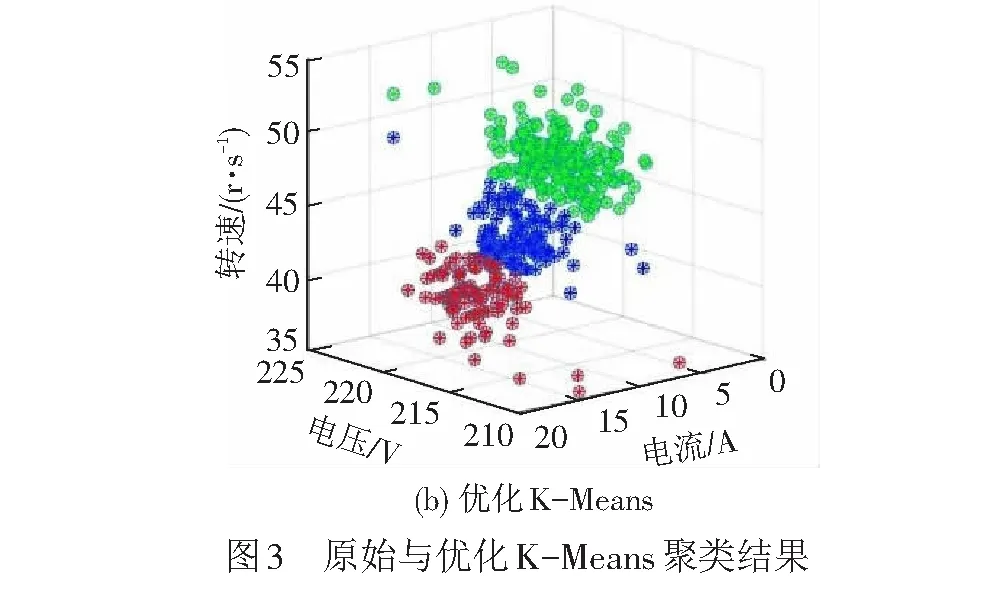
从聚类结果对比中可以看出，相较于传统的K-Means聚类，优化后的K-Means算法能够更好的将电机传动系统数据分为3个聚类。

表3 最终聚类中心

聚类之后计算出的3个类的类中心见表3，由表3可见，3个类中第1类的电压最大，电流也最大，然而转速却是最小的；这与第三类的结果恰好相反，电压最小，电流也最小，但转速却是最大；第2类中的3个数据都是3个类中的中间数据。基于电机工作原理[18]可知，电机是将电能转换为机械能的装置，其中，电流与电压的乘积可以表示电能，转速的平方可以表示机械能。因此，第1类中电流和电压比较大，转速反而小，说明电能供应多，但是转化的机械能比较少，可以反映出电机传动系统中存在着较大的内部阻力，也可理解为磨损较大，健康状态较差，进而判定第1类数据为电机故障情况下的数据；同理，第2类数据可以表示电机在中等磨损情况下的运行数据；第3类数据可以表示电机在健康情况下的运行数据。因此，将各个聚类与电机传动系统的状态评估相对应，见表4。

表4 电机传动系统状态说明

4 基于优化K-Means的健康状态评估实现

基于优化K-Means的健康状态评估框架见图5。

评估框架伪代码如下：

Input：Original data set(U,I,V)

Output：Target cluster label(Ⅰ,Ⅱ,Ⅲ)

1.Compute1(re_disk(p,o)&&loc_ou_fak(p))

2.Compute2(des(x)&ξ)→(x1,x2,x3)

3.Compute3(Distance &min(SSE))→new(x1,x2,x3)

4.Return cluster label Ⅰ,Ⅱ,Ⅲ

5.Use Add_nagios() &&Add_perfdata()→Icinga

6.Achieve health condition assessment

详细描述如下：

输入：{基于电流、电压、转速的三维数据集}

输出：{数据的聚类标签}

(1) 获取自动化装配线上的实际运行数据集。

(2) 使用LOF算法对原始数据集进行去噪，消除其中的噪声点与异常点。

(3) 通过计算数据集中每个样本点区域密度和高斯分布的覆盖半径，依次选择出3个样本点作为初始中心点；并且在中心点更新上，将各簇中距簇内各样本点距离方差最小的点作为新的中心点。

(4) 使用add_nagios()接口与add_perfdata()接口将优化K-Means实现的聚类结果与icinga监控平台进行通信。

(5) 根据输出的聚类标签进行状态识别，完成设备健康状态评估。

本论文根据上述框架实现了高速列车自动化装配线中对自动化立体仓库的监控，根据举升电机、翻转电机、行走电机传动系统的实际运行数据对三者的健康状态进行评估，共分为3个状态，正常、警报与严重，分别对应优化K-Means聚成的3个类，系统中分别以绿色、黄色、红色表示，部分展示界面见图6。

5 结束语

本文针对原始K-Means算法中对数据异常点过于敏感的问题，提出了基于局部异常因子算法的优化方法，有效地去除数据噪声点的影响；针对中心点选取过于随机性的缺陷，提出一种新的中心点选取方法，即通过计算样本点区域密度，选择出K个初始中心点，并且新中心点是选取距簇中其他样本点方差最小的点，从而改善了聚类效果。通过实际项目中电机传动系统的电流、电压、转速数据证明，优化后的K-Means算法使得类间距离变大，类内距离变小，聚类效果较好，并且，将这种优化的K-Means算法用于实际的监控系统，实现了对电机传动系统的健康状态评估。这种基于K-Means的优化算法需要计算区域密度，随着数据量的不断加大，将会显著增加计算开销，可以利用数据并行计算方法提高计算效率。