基于广义费用函数的城际铁路分时定价策略研究

景 云， 孙佳政， 张桢桦

(1.北京交通大学 交通运输学院，北京 100044；2.中国雄安集团基础建设有限公司，河北 保定 071700)

城际铁路作为城市群各城市间居民出行的主要方式，具有运量大、便捷性好、可靠性高、低碳环保等特点，有效缩小了城市间的时空距离，带动了城市间经济的发展。随着城市群内部各城市间客流需求的不断增长，城际铁路客流量出现了明显的高峰期和低谷期，高峰时段客流量过大，造成购票困难，服务质量下降等现实问题，低峰时段客流量较少，造成了运能浪费和企业收益减少等问题。城际铁路客流可分为生产型和非生产型两类：生产型客流出行目的主要包括工作、商务等，此类客流对运输服务的质量要求较高，对运输费用的敏感度较低；非生产型客流出行目的主要包括旅游、探亲等，此类客流对运输费用敏感度较高，对出发时刻敏感度不高。因此，可以通过对城际铁路采用分时定价策略，利用票价调节对出发时刻敏感度不高的旅客，从而达到“削峰填谷”，提高城际铁路运输服务质量的目的。

目前，国内外对轨道交通票价方面的研究主要集中在票价对旅客出行行为的影响和票价的调节方式两方面。Vuuren[1]提出采用铁路高峰时段和低谷时段差别定价的方法可吸引更多旅客至低谷时段，起到“削峰填谷”的作用。Shaffer等[2]主要对旅客类型进行划分，将旅客划分为稳定和不稳定两种，其中稳定型顾客对产品忠实度较高，不会选择其他可替代品；而不稳定型顾客则会因为各种外界因素改变选择。Whelan等[3]、Cosgun等[4]提出了一种在if-then模糊规则下，研究不同时段旅客对不同票价选择概率，从而求解最优票价以最大企业收益的计算方法。罗利等[5]则通过随机过程理论和最优控制理论求解连续出发时刻的同一航线与不同出发时刻航班的联合动态定价模型，从而获得最优联合定价策略，最后结合实例说明动态定价策略的实施可以为企业带来更大的利润。布超等[6]分析了交通方式的不同属性以及旅客个体间差异等因素与旅客时间成本的关系，建立了以票价和收入作为衡量旅客对票价敏感度衡量指标的时间成本改进Logit模型。张晓晴[7]基于早高峰客流数据，构建不同时间，不同运输方式的旅客广义出行费用函数，以不同时段的票价折扣率和客流量为自变量，构建了双层规划模型，并以PSO算法为基础的非数值优化算法求解模型。杨文静[8]通过研究轨道交通票价改变对客流量的影响程度，计算了不同出行需求的旅客价格需求弹性。贺亦丹[9]认为旅客对出行时间的选择决定了不同时间的客运量，铁路部门应该基于此规律制定不同票价，以获得更高收益；与之相反，票价的高低也会影响旅客出行时间的选择，从而对客流量造成影响，这是一个相互制约的复杂过程。

综上所述，目前城际铁路票价策略的研究主要集中在两个方面：利用收益管理理论，对预售期内票价制定策略研究，针对季节性的客流不平衡问题，对票价折扣进行研究：针对一天内城际铁路票价的制定策略研究较少。本文将构建双层规划模型，上层规划依据城际铁路运营实际情况，建立企业收益函数；下层规划针对一天内的客流特性，将城际铁路客流量划分为高峰、平峰和低谷多个时段，建立不同时段、不通运输方式的旅客出行广义费用函数。最后，结合粒子群和Frank-Wolfe的非数值算法求解不同时段城际铁路最优票价。

1 城际铁路分时定价双层规划模型

城际铁路分时定价策略就是通过对城际铁路运输服务时段进行划分[10]，然后根据不同时段的运输服务特性进行差别定价，从而提升运输服务质量，增加企业收益。在进行城际铁路各时段票价制定时，应结合客流客观规律，寻找不同时段城际铁路系统的最优票价，并分析由于票价浮动造成的客流变化情况。因此，构建了以城际铁路运输企业收益最大为上层目标，以乘客出行广义费用最小为下层目标的双层规划模型，以确定各时段的最优定价策略[11]。

1.1 模型假设

基于双层规划的分时定价模型，重点围绕客流与票价之间的关系进行优化，因此需要对城际铁路运输服务过程中的一些影响因素进行假设。

(1) 城际通道内客流总量不变。

(2) 城际铁路列车运行图固定，且各个时间段内均匀发车。

(3) 每个时间段内旅客均匀到达。

(4) 城际铁路连接两个中心城市，中途不停站。

(5) 旅客出行行为完全理性，运输信息全部已知，旅客始终会选择自身广义费用最小的交通方式出行。

1.2 上层规划模型

城际铁路运营商的利润取决于票价、客流量、旅客平均运输成本、城际列车每次发车固定成本等因素，据此建立以运营商利润最大为目标的上层规划模型。

(1)

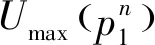
城际铁路票价取决于线路的速度等级、里程以及折扣等方面的因素，铁路部门在进行票价的制定时对其上限和下限都有着明确的规定。因此，上层规划模型的约束条件主要是票价上、下限约束。

(2)

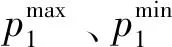
1.3 下层规划模型

1.3.1 下层规划旅客广义出行费用模型

旅客出行的广义费用是对旅客在运输过程中经济利益流出较为全面的估算。根据文献[11]，广义费用函数为

(3)

(4)

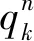
在分时定价双层规划模型中，基于上文假设，不考虑随机部分。则效用函数可以简化为

(5)

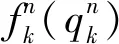
双层规划的下层模型为

(6)

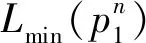
由于城际旅客广义出行总费用受到城际通道内旅客数量以及不同运输方式的运输能力限制，所以下层规划的约束条件为

(7)

1.3.2 广义费用函数构建

(8)

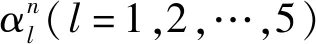
快捷性衡量指标是完成一次出行的时间成本，包括运行时间和衔接时间。由于城际铁路旅客不存在中间换乘的情况，所以衔接时间为零。因此在进行快捷性指标计算时只对旅客在列车运行过程中的时间消耗进行计算，即

(9)

(10)

旅客方便性衡量指标是指城际旅客从出发地到车站以及从车站到目的地的城市内交通消耗时间，进出站消耗时间以及上下车消耗时间。客流高峰时段，人流量的增加会使旅客的市内交通消耗时间和进出站消耗时间增加，即

(11)

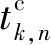
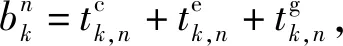
(12)

旅客舒适性主要取决于列车旅行时间、软硬件服务设施等因素。舒适性这一指标依赖于旅行时间，它可以用旅客恢复疲劳所需的时间来量化。一般旅行时间越长，旅客由疲劳状态恢复所需要的时间越长，其舒适性越差，反之舒适性越好；另一方面，列车越拥挤，舒适性越差，反之舒适性越好。旅客由疲劳状态恢复所需时间的函数[12]为

(13)

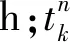
(14)

运输服务的可靠性主要指运输服务的准点率，用不同时段指定运输方式的平均延误时间表示

(15)

安全性也是影响旅客出行方式和出行时段选择的重要因素，不同交通方式交通事故发生概率是安全性的主要衡量指标。

(16)

2 算法求解

城际铁路分时定价问题可以看作一个领导者和一个追随者的问题，在其他运输方式票价不变的前提下，城际铁路票价制定的领导者是运输企业，追随者是各时段的旅客。上层规划是领导者，决策变量是各时段的票价，运输企业者通过票价影响旅客出行方式和出行时段的选择；下层规划是追随者，决策变量是各个时段各种运输方式的客流量，下层旅客在上层票价的决策下做出选择，下层旅客的选择又进而影响上层票价决策，最终到达双方平衡[13]。本文结合Frank-Wolfe(F-W)算法[14]和粒子群算法[15]求解双层规划模型。算法流程见图1。

算法步骤如下：

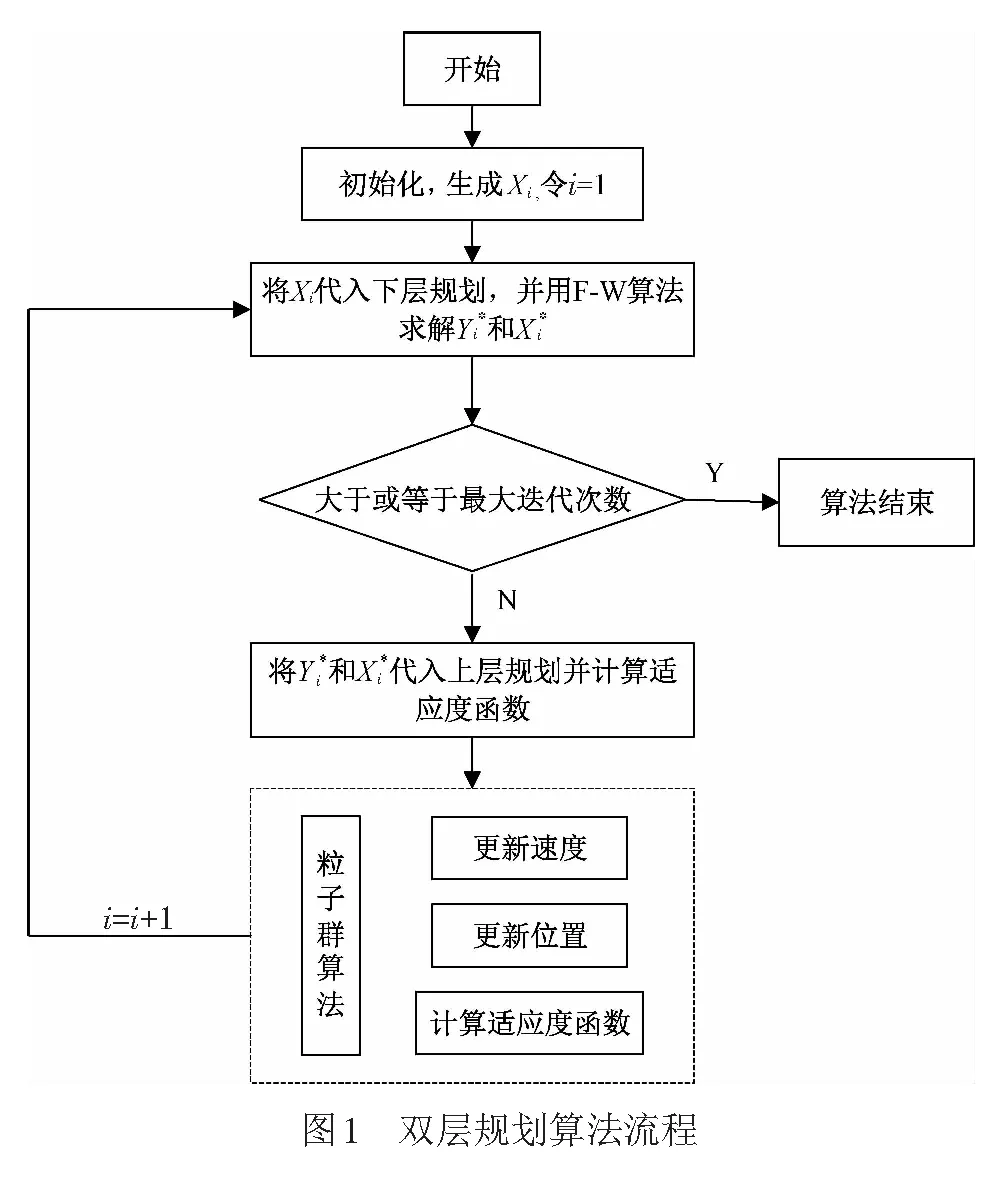
Step1初始化粒子群。生成粒子群，群体规模记为N，记录当前每个粒子位置Xi和速度Vi，并将最大迭代次数设为Ggen，令i=0。

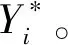
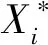
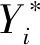
Step5逐次更新粒子位置，得到新一代粒子位置，Xi=Xi+1。令i=i+1，转Step2。

3 算例分析

京津城际铁路运营里程166 km，属于中短途运输，在中短途客运市场中铁路和公路具有较强的竞争优势。

结合京津铁路运营情况，首先，将其运营时间划分为16个时段，并按照时间顺序对时段进行编号，可得n∈{1,2,…,16}；然后，按照京津城际列车各时段的平均载客率将16个时段划分为低谷、平峰和高峰3种类型[16]，划分标准见表1。

表1 各时段类型划分标准

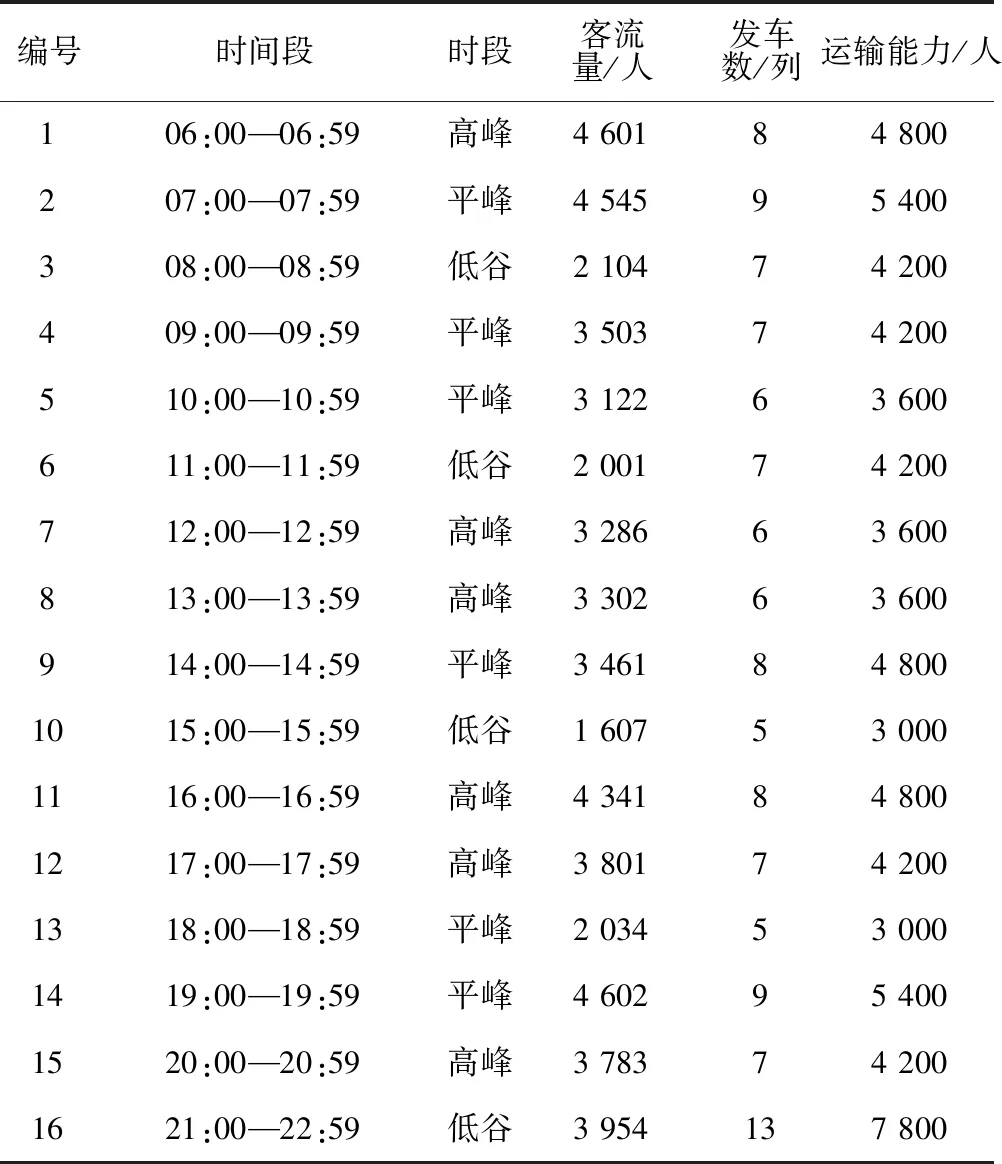
表2 某日京津区域城际铁路客流与运能数据

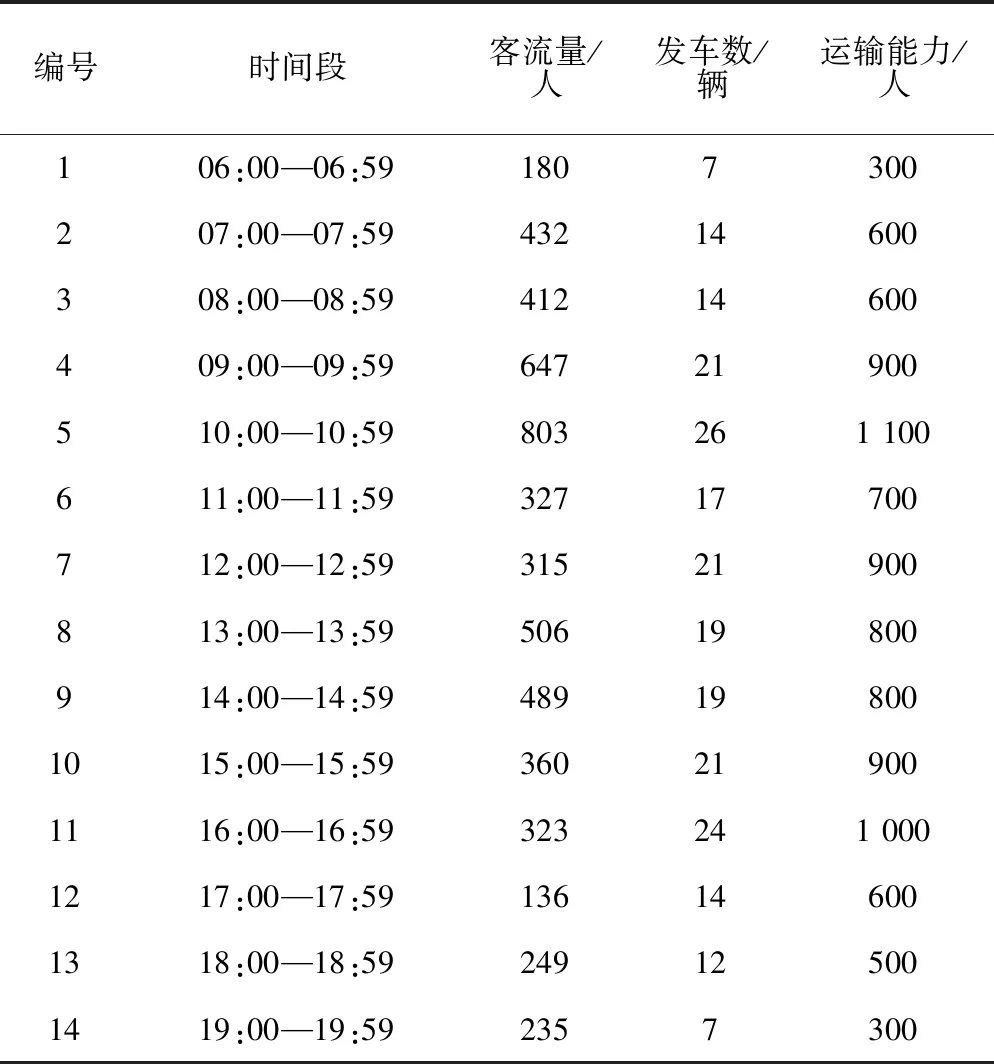
表3 某日京津区域公路公交客流与运能数据

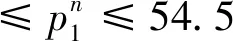
通过对京津城际旅客进行问卷调查，获得不同时段旅客对运输属性的偏好权重见表4。

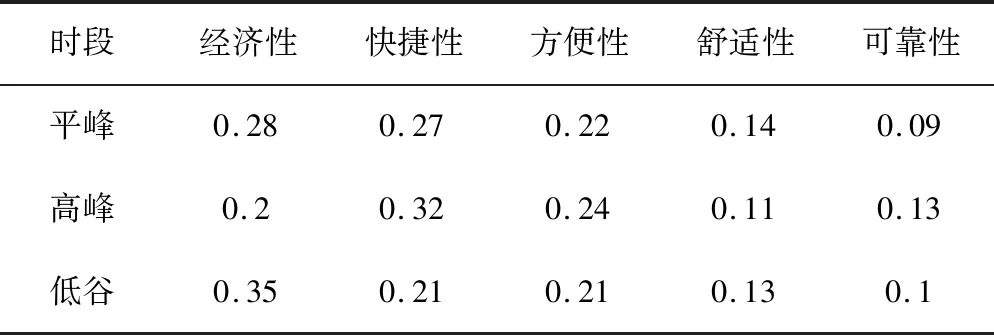
表4 各时段旅客对运输属性偏好权重

通过调查问卷的计算结果，得到不同时段旅客的时间成本见表5。

表5 各时段旅客时间成本 元

城际铁路和公路不同时段旅客旅行过程消耗时间见表6。其中，在舒适性计算中，H取15 h，城际铁路、公路的αk、βk取值分别为(59，39)，(0.29，0.40)。

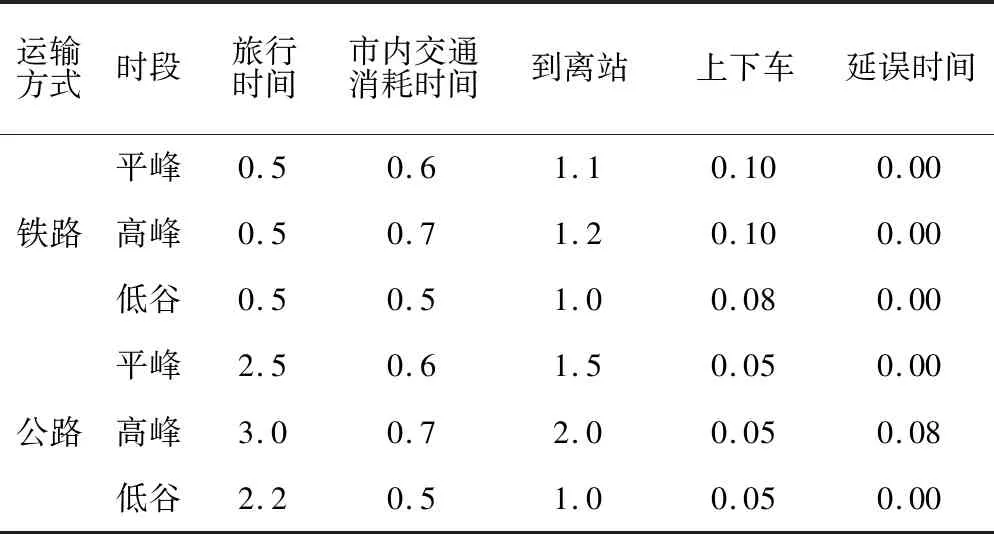
表6 不同时段城际铁路和公路旅客旅行过程消耗时间 h

表7 不同客流状态下城际铁路和公路安全性取值

在粒子群算法中，粒子种群N=100，最大迭代次数Ggen=100，粒子维数D=16，学习因子c1=0.5，c2=1，惯性权重wmax=0.8，wmin=0.3，粒子速度vmax=1.5，vmin=-1.5。利用Matlab编程计算可以获得上、下层目标函数收敛曲线见图2，随着迭代次数的增加最优解和目标函数会不断改变，当最优解与目标函数基本保持稳定时，说明双层规划模型达到收敛状态。

由图2可知，模型逐步收敛，上层目标逐步增大，下层目标不断减小。当迭代220次时，最优解和目标函数基本保持稳定，铁路部门最大收益为73.41万元，旅客广义出行费用最小为323.83万元。城际铁路各时段定价结果见表8。

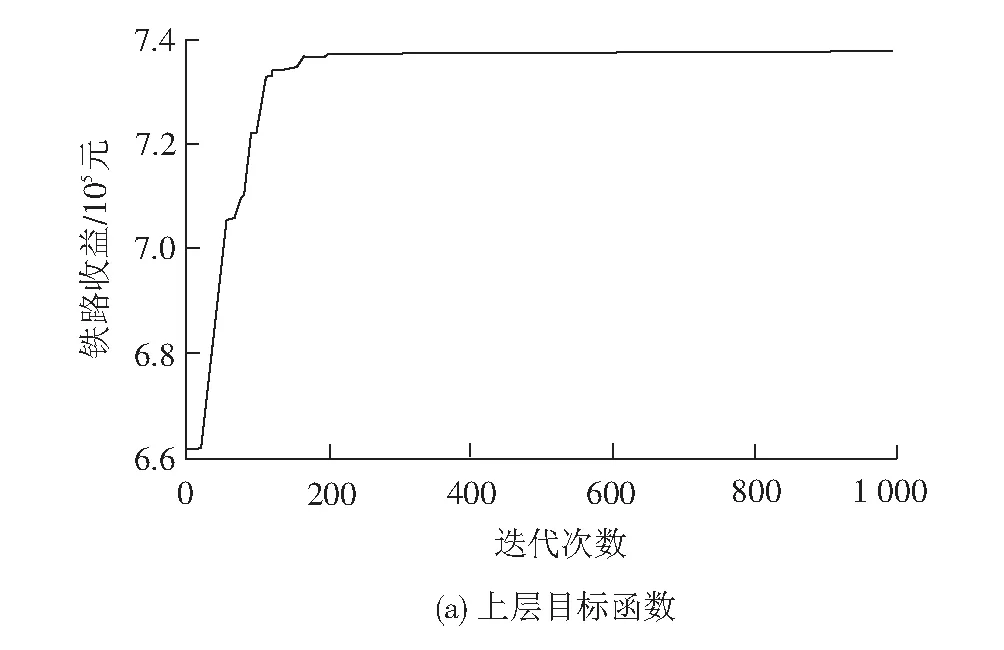
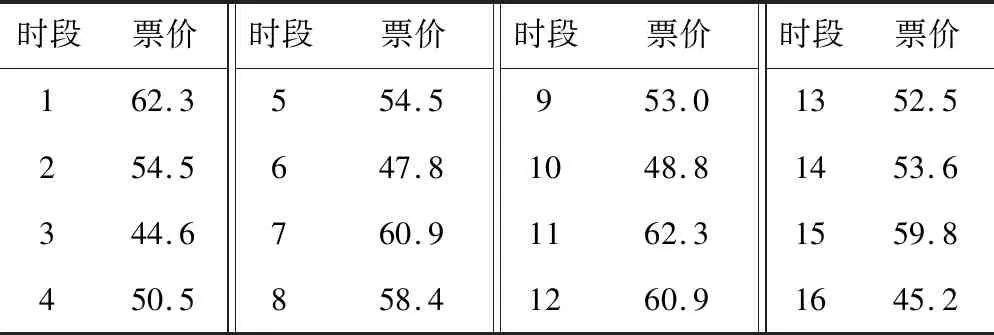
表8 城际铁路各时段票价 元

将统一定价策略下的票价与分时定价策略下的票价进行对比，可获得京津城际铁路不同时段票价的对比,见图3。

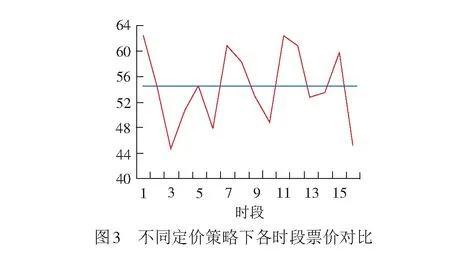
图3中，分时定价模型可以根据不同时段客流情况制定不同的票价，客流高峰时段票价较高，低谷时段票价较低，时段1(06:00—6:59)和时段11(16:00—16:59)票价最高，为62.3元；时段3(08:00—8:59)票价最低，为44.6元。客流高峰时段票价较统一定价时更高，引导旅客向平峰、低谷时段转移；低谷、平峰时段票价较统一定价更低，吸引出行时间灵活的旅客改变出行时间。

分时定价策略下各个时段的城际铁路客流分布见表9。

表9 城际铁路各时段客流分布

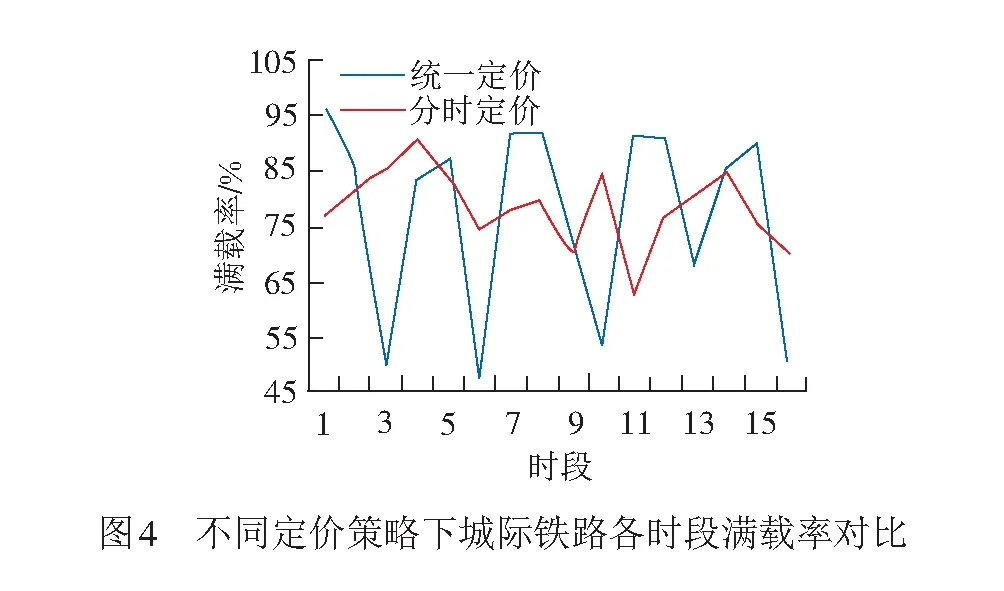
将统一定价策略下城际列车满载率与统一票价下城际列车满载率进行对比，获得京津城际铁路不同时段间两种定价策略的列车满载率对比图，见图4。

图4中，分时定价策略实施后，京津城际铁路列车除时段4(09:00—9:59)外其余时段满载率均在60%～90%之间，所有时段都达到了平峰状态，其中时段11(16:00—16:59)满载率增加最为明显为27.68%；时段3(08:00—8:59)满载率降低最为明显为34.98%。说明分时定价策略的实施使可以客流分布更加合理、均衡，有助于提高运输服务质量。

将分时定价策略下的客流量与统一票价下的客流量进行对比，可以获得京津城际铁路不同时段间两种定价策略的客流对比，见图5。

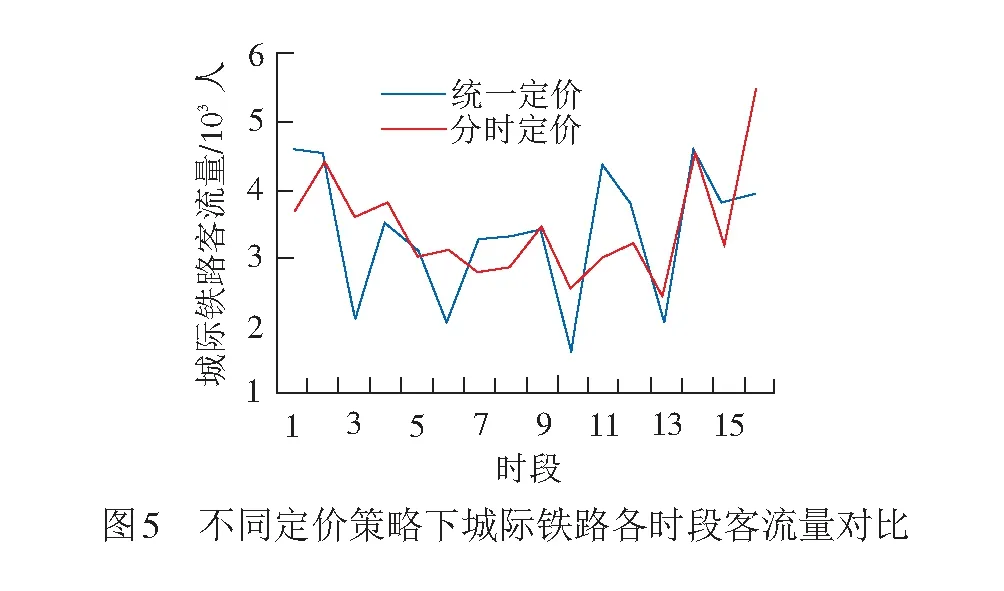
图5中，采用分时定价策略后，各时段客流变化较统一定价时更为平稳。高峰时段客流量在原有客流基础上有所下降，时段11(16:00—16:59)客流转移率最高，达到30.61%；低谷时段在原有客流基础上有所增长，时段3(08:00—8:59)客流增长最大，达到69.84%。在铁路运能不变的情况下，分时定价策略的实施吸引了更多通道内客流，实施分时定价策略前，京津城际铁路一天内运输旅客54 047人次；实施分时定价策略后，京津城际铁路一天运输旅客54 960人次，增长幅度为1.69%。在铁路运输企业收益方面，实施分时定价策略后铁路运输企业收益增长了1.99万元/日。因此，分时定价策略的实施一定程度上发挥了票价对客流的调节和引导作用，增加了铁路运输企业的收益。

4 结论

为解决城际铁路客流分布不均衡问题，本文利用分时定价策略，以城际铁路运输企业效益最大为上层规划目标，以旅客出行广义费用最小为下层规划目标，构建基于旅客广义出行费用的城际铁路分时定价模型，并结合粒子群算法和Frank-Wolfe算法求解，得到各时段最优票价及转移客流量。通过算例分析发现，相较于统一定价，分时定价策略可以有效诱导旅客对出发时段的选择，为城际铁路运输企业吸引了更多客流，从而提高企业收益。在双层规划模型构建时，本文假设了通道内客流保持不变，而对于弹性需求下的定价策略仍需继续探究；在案例分析时，对京津城际铁路的实际情况采用了理想化的假设，未来应进一步研究更加符合铁路现场实际的动态票价制定方法，提升铁路运营企业效益水平，改善旅客出行服务品质，实现铁路和旅客耦合系统效益最大化的目标。