基于直接刚度法的弹性地基深梁单元

丁 敏， 李 静,2，罗 双,3 ， 曹琼琼,4

(1.中国农业大学 水利与土木工程学院，北京 100083；2.河南职业技术学院 环境艺术工程学院，河南 郑州 450046；3.中国农业科学院 基本建设局，北京 100081；4.中国国家铁路集团有限公司 铁总服务有限公司，北京 100844)

弹性地基梁是指除梁端或梁中某些点存在特定形式支座约束外，梁中存在连续位移约束的梁。考虑弹性地基梁中剪切变形影响的梁模型称为弹性地基深梁。弹性地基深梁是铁路工程结构中常见的计算模型之一，其理论被广泛应用于铁路轨枕、道床等结构计算中。

根据不同的地基反力假设，学者们提出了不同的弹性地基模型，常用的弹性地基反力模型有Winkler弹性地基模型和双参数Pasternak弹性地基模型[1-3]。Winkler弹性地基模型假设地基反力与该点位移成正比，忽略了地基剪切变形对地基反力所造成的影响。双参数Pasternak弹性地基模型中假设地基反力与挠度及挠度的二阶导数有关，从理论上改进了Winkler弹性地基模型不连续的缺陷。

夏桂云等[4]总结了深梁理论、深梁线性和几何非线性有限元、弹性地基深梁等在工程结构中的应用，提出用Timoshenko深梁理论进行重建、重写杆系结构静力和动力分析的方法。最经典的深梁计算理论是Timoshenko于1921年提出的两广义深梁理论[5]。此后很多学者根据不同的位移模式，建立了不同的深梁理论，包括零阶剪切变形理论[6-7]、三阶剪切变形理论[8-12]等。Timoshenko深梁理论认为，在直梁发生变形前垂直于直梁中心线的截面，变形后仍为一个平面，但不再假定该截面仍垂直于变形后的中心线，即直梁变形后截面转角θ与梁轴线转角φ不相等，二者的差则为剪切角。基于Timoshenko深梁理论，学者们构造出了一系列深梁单元[13-14]，但是这些模型都是针对普通深梁，主要通过多项式形函数求解其位移及内力。与普通深梁不同，弹性地基深梁上存在与地基梁挠度方向相反的反力，反力大小由挠度确定[15]，所以相比于一般深梁，弹性地基深梁的受力变形控制方程更加复杂，其内力与变形计算更加复杂和困难。

弹性地基深梁分析方法主要为普通深梁单元加足够多弹簧支座的计算方法、将地基梁模拟为普通杆件通过加连续支承体结合刚性链杆的链杆法[16]、假定地基变形单独考虑地基反力的修正刚度矩阵解法[17]，通过这些方法想要得到连续支承的分析计算模型，都需要将梁分成足够多的单元，才可得到连续支承的分析计算模型。目前对弹性地基Euler梁以及单参数弹性地基Timoshenko梁的研究已经取得了相当多的研究成果[18-23]。Onu[24]将横向变形分解为弯曲变形和剪切变形，采用双挠度理论，得到双参数弹性地基Timoshenko梁的微分方程及有限元刚度矩阵，然后分析了弹性地基梁和结构-地基相互作用问题。Shirima等[25]考虑了水平摩阻的影响，分析了Fionenko-Borodich模型和Pasternak模型Timoshenko梁问题。夏桂云等[26-27]建立了考虑地基摩阻的Winkler地基和双参数地基Timoshenko梁的初参数法和有限元法。李静[28]建立了解析型弹性地基Timoshenko梁单元，可用于单参数、双参数的Euler梁和Timoshenko梁的计算。

直接刚度法是用于求解一般梁体系的一种常用方法，最早由Clough提出[29]。与有限元法[30-32]不同的是，直接刚度法没有假定梁内位移方程的表达式，二者虽具有相同的适用性，但直接刚度法分析精度更高。本文充分考虑了双参数Pasternak弹性地基深梁的受力、变形特征，推导得到弹性地基深梁的挠度控制方程及其全解，根据节点内力方程，利用直接刚度法解得弹性地基深梁的刚度矩阵，并给出了均布荷载的等效节点力向量。结合弹性地基深梁刚度矩阵，可直接求解得到弹性地基深梁的内力及真实位移，为弹性地基深梁解析解的计算提供了理论依据。

1 基本原理

1.1 弹性地基深梁及其物理量

弹性地基深梁坐标系定义见图1。

轴向坐标x向右为正，挠度位移坐标z向下为正，坐标零点位于梁左端。依据右手螺旋法则，y轴指向平面外侧为正。梁位移、荷载的正方向均与坐标轴方向一致为正，转角位移逆时针为正。

当截面法线为x轴正方向时，梁内力与坐标方向一致时为正、方向相反时为负；当方向不同时相反为正。

对于弹性地基深梁，梁的物理量包括:

几何参数：宽度b，高度h，长度l；刚度参数：截面抗弯刚度EI，抗剪刚度GbA。

荷载参数：集中力P，均布力qz，集中力矩M；内力参数：梁截面弯矩M(x)，截面剪力V(x)。

位移参数：梁的挠度为w，截面转角为θ，梁轴转角为φ，截面剪切角为γ，截面曲率为κ。

节点力向量

节点位移向量

1.2 弹性地基反力模型

在双参数弹性地基深梁中，地基反力方向与地基变形方向相反，在单位面积的反力值表达式可写为

p(x)=kw(x)-Gpw″(x)

(1)

式中：k为地基压缩刚度系数；Gp为深梁剪切刚度系数。

当地基剪切刚度Gp=0时，双参数地基模型退化为典型的单参数模型即Winkler弹性地基模型。

1.3 控制方程

弹性地基深梁的基本方程为:

(1) 几何方程

梁轴转角

φ=-w′(x)

(2)

φ=θ-γ

(3)

截面曲率

κ=-θ′(x)

(4)

(2) 平衡方程

力矩平衡方程

M′(x)=V(x)

(5)

力平衡方程

V′(x)=-q(x)

(6)

式中：q(x)=qz(x)-p(x)。

(3) 物理方程

弯曲刚度方程

M(x)=-EI·κ

(7)

剪切刚度方程

(8)

式中：μ为截面不均匀剪切系数

将式(7)、式(8)及式(1)代入平衡方程式(5)，再对曲率求二阶导数，经整理，得到了以挠度表示的弹性地基深梁挠度控制方程

wⅣ(x)+2λ2(α2-β2)w″(x)+4λ4w=

(9)

式中：

由将基本方程式(4)、式(5)、式(7)代入式(8)，可得平衡协调方程为

(10)

2 微分方程求解

当qz(x)取常数q时，求式(9)，得其全解为

(11)

式中：

f1(x)=eβλxsin(αλx)

f2(x)=eβλxcos(αλx)

f3(x)=e-βλxsin(αλx)

f4(x)=e-βλxcos(αλx)

显然

α2+β2=2

(12)

f′=fZ

(13)

(14)

φ(x)=-fZc

(15)

式中：

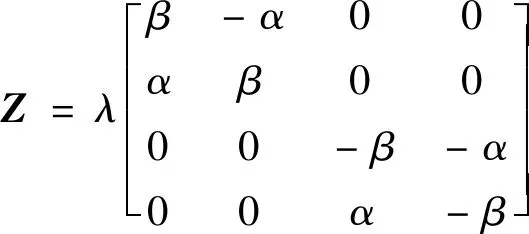
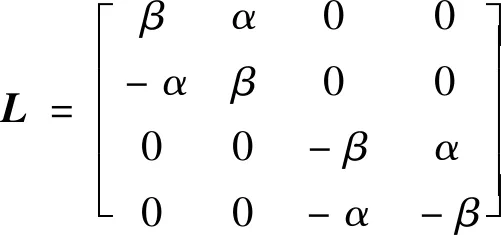
则有

LZ=ZL=2λE

(16)

3 位移系数定解

利用截面剪切角与截面转角的关系，即平衡协调方程式(10)，可求得积分常数c0，从而可进一步解得弹性地基深梁截面剪切角和截面转角的方程。

3.1 截面剪切角

由式(1)、式(6)及式(8)，可以得到深梁的截面剪切角导数方程为

(17)

经积分，可得

(18)

3.2 截面转角

由式(2)、式(3)及式(18)，可得深梁的截面转角方程为

(19)

则有

(20)

由式(10)、式(18)及式(20)，可解得积分常数为

(21)

将式(21)代入式(18)，可得梁截面剪切角方程为

(22)

将式(21)代入式(19)，可得梁截面转角方程为

θ(x)=fYc

(23)

式中：

进一步，则有

θ′(x)=fZYc

(24)

θ″(x)=fZZYc

(25)

根据深梁各截面位移计算公式和定解条件，可得位移系数定解方程

(26)

式(26)可简化为

Ac=δe+δq

(27)

式中：

Fl=[eβλlsin(αλl) eβλlcos(αλl)

e-βλlsin(αλl) e-βλlcos(αλl)]

由定解方程式(27)，可以得到位移系数为

c=A-1δe+A-1δq

(28)

4 刚度矩阵

由式(4)、式(7)和式(24)，可得梁内力为

M(x)=EIfZYc

(29)

由式(5)和式(25)，可得

V(x)=EIfZZYc

(30)

根据梁变形量的定义，梁端力与梁端内力的关系为

(31)

根据内力计算式(29)和式(30)，梁端力可表示为

Fe=EIDc

(32)

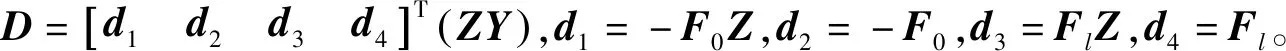
由式(29)和式(32)，节点力向量可表示为

Fe=Kδe+Fq

(33)

式中：刚度矩阵为K=EIDA-1；等效节点力为Fq=-EIDA-1δq。

由式(33)可得

δe=K-1Fe+K-1Fq

(34)

根据式(34)，结合刚度矩阵及等效荷载向量，可求得弹性地基深梁的节点位移。将节点位移代入式(28)，可得位移系数

从而可以得到弹性地基深梁的挠度曲线方程。

5 算例及分析

5.1 合理性分析

为了验证由直接刚度法构造的弹性地基深梁单元的合理性，分别计算在不同荷载工况下弹性地基深梁梁端挠度及截面转角。算例中梁结构参数见表1，荷载工况见表2。

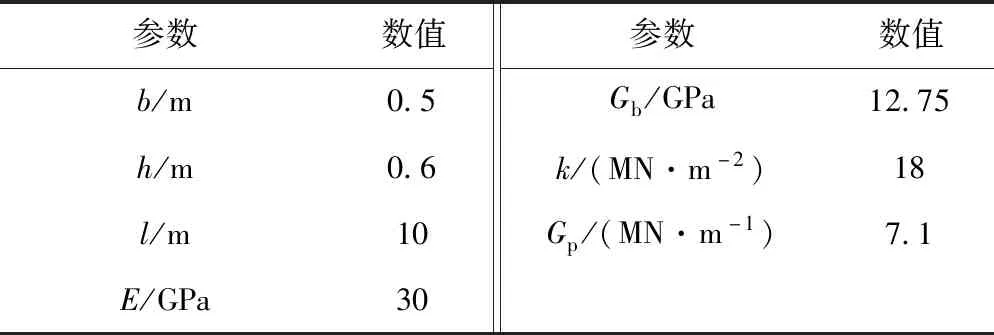
表1 弹性地基深梁结构参数

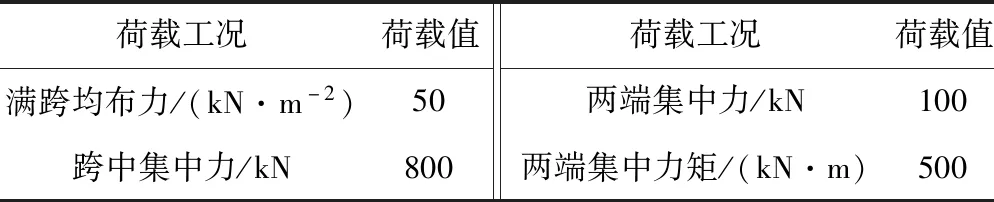
表2 荷载工况

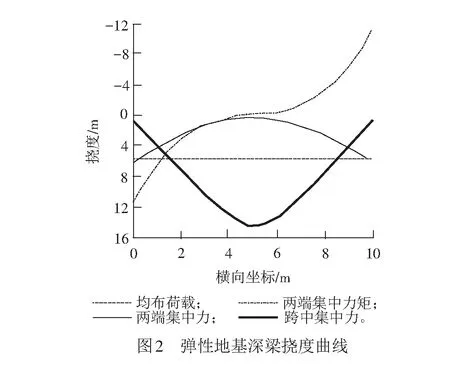
利用直接刚度法求得的在均布荷载、两端集中力、两端集中力矩、跨中集中力分别作用下的弹性地基深梁的节点位移计算结果见表3，根据节点位移解得弹性地基深梁的挠度曲线见图2。由图2可见，在均布荷载作用下，弹性地基深梁各点挠度相等，相当于刚体位移，梁轴转角及截面转角为0。在两端集中力作用下，弹性地基深梁两端挠度最大，中点处挠度最小，梁挠度曲线关于梁中垂线对称。在两端集中力矩作用下，弹性地基深梁两端挠度绝对值最大，中点处挠度和截面转角为0，梁挠度曲线关于梁中点中心对称。在跨中集中力作用下，弹性地基深梁两端挠度最小，中点处挠度最大，梁挠度变形曲线关于梁中垂线对称。图2中弹性地基深梁在各种荷载下挠度曲线进一步验证了直接刚度法构造的弹性地基深梁单元的合理性。

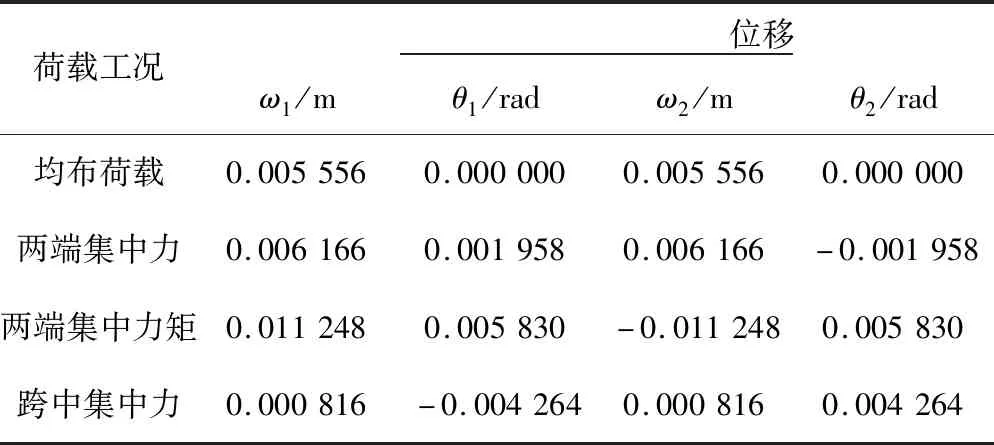
表3 弹性地基深梁节点位移计算结果

不同梁高时，本文模型计算出跨中集中力作用下的弹性地基梁的中点挠度及中点截面转角见表4。其中，模型1中考虑了剪切变形的影响，将梁的剪切模量取为结构实际参数，模型2中不考虑剪切变形的影响，将梁的剪切模量取为无穷大。随着梁高从0.5 m逐渐变为2.0 m时，剪切变形影响从1.152%变为1.659%，截面转角均为0。可见，随着梁高的增加，剪切变形对梁中点挠度的影响变大。

表4 不同梁高下弹性地基梁中点位移(跨中集中力P=1 000 kN)

注：模型1中参数采用的是结构实际参数Gb=12.75 GPa；模型2中将表1中梁剪切模量放大百万倍，Gb=12.75×106GPa；剪切变形影响=(模型1计算值-模型2计算值)/模型1计算值×100%。

5.2 适用性分析

当Gb→时，基于直接刚度法构造的弹性地基深梁单元可用于计算弹性地基Euler梁；当Gp→0可用于计算Winkler弹性地基梁。本文单元可用于Winkler、Pasternak弹性地基模型与Euler梁、Timoshenko深梁组合的4种弹性地基梁的计算。

为了验证本文单元的适用性，将直接刚度法得到的弹性地基深梁单元分别用于双参数Pasternak弹性地基Euler梁、Winkler弹性地基Euler梁的计算，并与文献[30]和文献[29]中解析法计算所得结果进行对比，计算及对比结果见表5。在本文算例中，Pasternak弹性地基Euler梁将表1中梁剪切模量放大百万倍，取Gb=12.75×106GPa；Winkler弹性地基Euler梁取Gb=12.75×106GPa，Gp=0。

由表5可见，用直接刚度法求解Pasternak弹性地基Euler梁和Winkler弹性地基Euler梁时计算值分别与文献[30]、文献[29]中解析法的计算值完全一致，说明直接刚度法适用于单、双参数的Euler梁、Timoshenko弹性地基梁的计算，且不存在剪切闭锁的问题。

需要说明的是，本文提供的单元对于承受均布外力的弹性地基梁是一个“精确”单元，未考虑单元内承受集中力和集中力矩，因此在运用本单元时应注意：当作用有集中力和集中力矩的截面，应布置节点、划分单元；当作用有非均布的分布荷载时，应按两端固端力相等的原则，将非均布力等效为均布力进行计算。

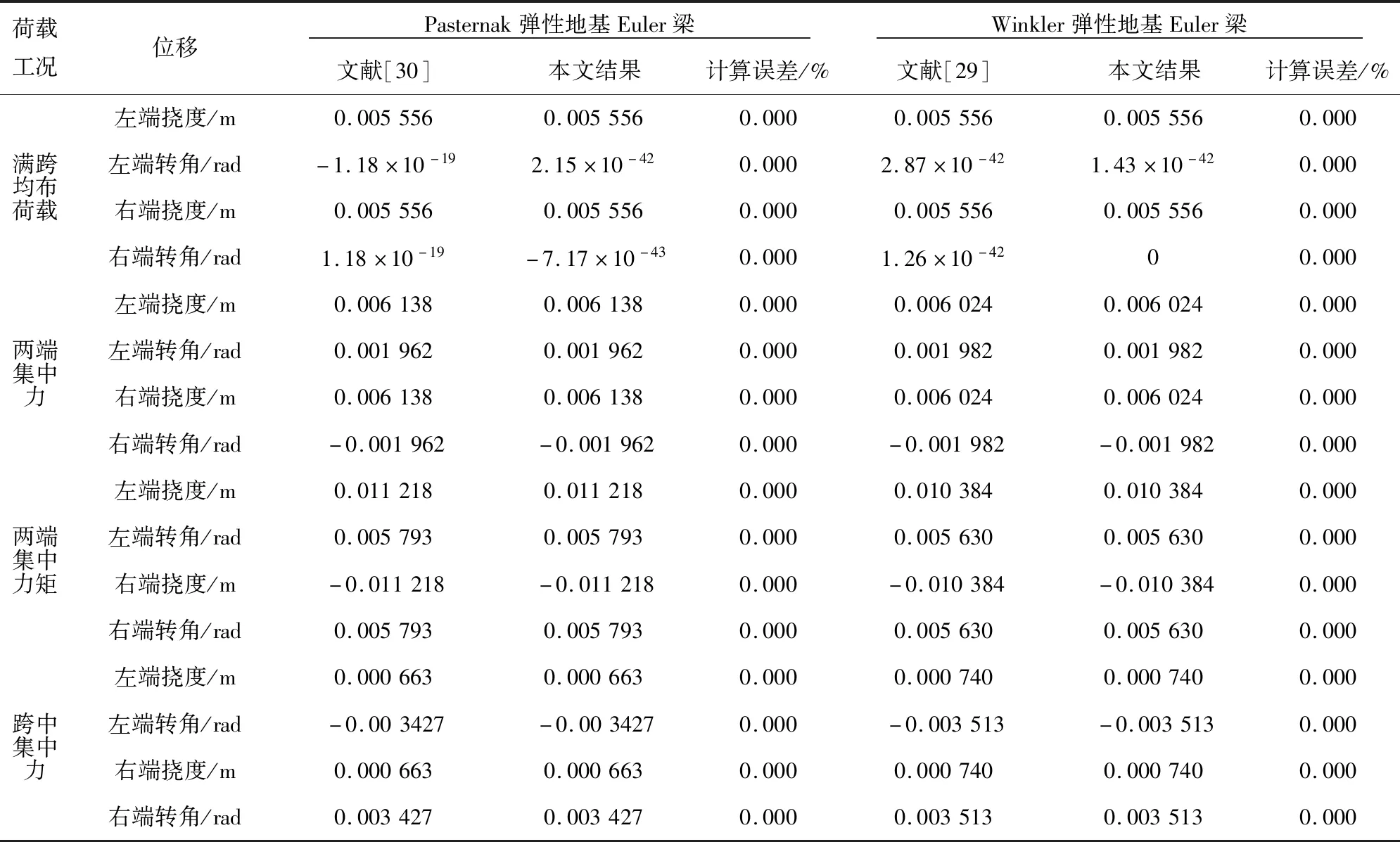
表5 Pasternak、Winkler弹性地基Euler梁计算结果

6 结论

(1) 基于双参数弹性地基深梁的基本方程，建立了弹性地基一般梁的挠度控制方程，并求得了截面剪切角以及截面转角的表达式。

(2) 利用节点位移条件，求解得到了用矩阵形式表达的位移系数，进而得到了双参数弹性地基位移的一般格式。

(3) 根据节点力方程，建立了刚度平衡方程，给出了刚度系数矩阵及等效节点力向量。

(4) 直接刚度法所构造的弹性地基深梁单元具有适用性广的特点，直接可用于不同地基模型：Winkler弹性地基模型、Pasternak弹性地基模型与不同梁模型：Euler梁、Timoshenko深梁组合弹性地基梁的计算，并且没有剪切闭锁的问题。