流动聚焦微通道内牛顿微液滴在幂律剪切致稀流体中的生成研究
2020-05-28陈琦李京坤宋昱何倩DavidChristopher李雪芳
陈琦,李京坤,宋昱,何倩,David M Christopher,李雪芳
(1 山东大学热科学与工程研究中心,山东济南250061; 2 清华大学能源与动力工程系,北京100084)
引 言
微流控技术是指在微米尺度对流体进行操控的一种技术,它可以将生物、化学实验室微缩到一个几平方厘米的芯片上。微流控液滴技术是其中的一个重要分支,它利用两种互不混溶流体间的相互作用将离散相分割成多个微小体积的液滴,并使其分散在连续相之中。微流控液滴技术具有以下优势:(1)液滴被连续相包覆,样品无扩散,浓度和反应环境稳定,可以避免交叉污染;(2)液滴体积小,试剂消耗少,可以减少来源少、价格昂贵试剂的使用;(3)液滴比表面积大,反应时间短,具有较高的传热传质效率;(4)可以实现液滴的精准控制和快速批量生产,生产速率可以达到十几千赫[1-2]。
自从Thorsen 等[3]提出使用T 型微通道来生产单分散液滴以来,大量的研究者开始关注和研究这种新型的液滴生成方式。微通道中的两相流动是微流控液滴技术的基础,研究内容涉及流型、生成动力学及参数预测等。研究表明,微通道中两相流动有三种基本流型:挤压状[4]、滴状[5]和射流状[2,6]。Xu等[7-9]发现只有当离散相流体与通道壁面间的接触角大于90°时才能生成规则液滴,否则只会形成两相液膜,液滴的大小与两相流率、黏度和界面张力等因素有关。Anna等[10]在T型通道的基础上提出使用流动聚焦微通道来进行液滴制备,相比T型通道,它可以更高频率地制备体积更小的微液滴,但该方式原理更复杂,液滴大小和频率更难以控制。
近年来,随着微流控技术在化工、生物及医学等领域内的广泛应用,研究开始向使用非牛顿流体作为离散相或连续相的方向发展。Fu 等[11]研究了聚焦通道中微气泡在剪切致稀流体中的破碎机制,表明连续相的流变特性会对微气泡的破碎形态和气泡大小产生显著影响,并给出了相应的预测模型。Rostami 等[12]观察了硅油连续相中牛顿和非牛顿液滴的生成过程,研究了黏度比和离散相的流变特性对液滴状态及流型的影响,发现离散相的非牛顿特性也会明显影响微液滴的生成。张沁丹等[13]对流动聚焦通道内液滴在黏弹性流体中的生成进行了实验研究,发现液滴尺寸随连续相流率、毛细数及弹性数的增加而减小,随离散相流率的增加而增加,连续相弹性对液滴尺寸的影响相对较小,并在此基础上建立了液滴尺寸的预测关联式。Sontti等[14]和Shi等[15]针对T型微通道内幂律流体中的微液滴生成进行了数值模拟,研究了幂律流变参数对微液滴生成的影响。然而,T 型通道和流动聚焦通道内液滴或气泡的生成原理不尽相同,流动聚焦通道内以非牛顿流体作为连续相或离散相的研究仍不完备。
尽管在微流控液滴技术领域内已有众多研究,但涉及非牛顿流体的研究仍然偏少,不同研究者所得的结论也不尽一致,缺少公认的预测液滴生成尺寸、频率等重要特征参数的模型。本文采用开源CFD 软件OpenFOAM 模拟了微通道内牛顿流体的两相流动和幂律剪切致稀流体单相流动,通过与实验数据对比验证了模型的准确性。以此为基础计算了硅油微液滴在幂律剪切致稀流体中的形成过程,研究了连续相流变参数对微液滴破碎机制、生成尺寸和频率等的影响。研究结果对临床使用过程中幂律流体中微液滴制备和微通道设计具有一定的指导意义。
1 控制方程
1.1 连续性及动量方程
由于两相流动的复杂性,模拟做出如下假设:两相流体在微通道内表现为层流流动;流体均视为不可压缩流体且与外界不存在热交换;流动过程中起主导作用的是黏性力和界面张力,忽略重力作用。界面张力作为一个源项引入动量守恒方程。因此,连续性方程和动量方程可分别表示为
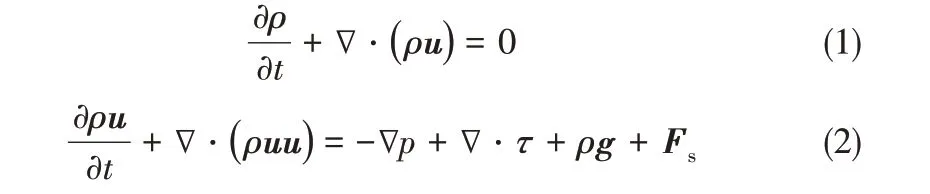
界面张力只作用于两相界面处,采用CSF 模型(continuum surface force)[16]进行计算

模拟通过定义壁面处的静态接触角(θw)考虑了壁面的润湿特性,壁面附近网格单元的界面法向量表示为[17]
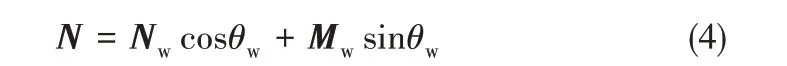
本文假设壁面被连续相完全润湿,设置连续相的壁面接触角为0°。
流动过程中的黏性剪切应力可表示为
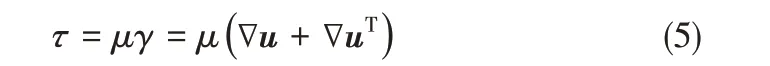
对于牛顿流体,其黏度为常数,黏性剪切力与剪切率呈正比。参考牛顿流体,定义了非牛顿流体的表观黏度为μ(γ)。本研究所用的幂律模型的本构方程为

当n <1 时表示剪切致稀流体,n = 1 时表示牛顿流体,n >1时表示剪切致稠流体。
1.2 VOF模型
相界面的捕获通过定义一个相分数α 来实现,α = 1 表示网格单元全部被离散相占据;α = 0 表示网格单元全部被连续相占据;0 <α <1 表示两相界面。在计算过程中,式(1)和式(2)中的密度和黏度均为混合属性,并通过式(7)和式(8)计算
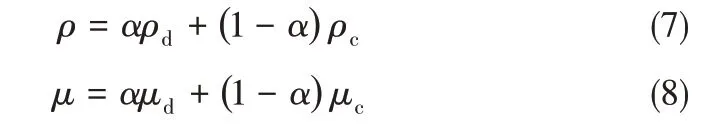
两相体积分数α可通过式(9)计算获得

在VOF 模型中,相分数α 作为一个特殊的被动标量,数值上必须保证在0 ≤α ≤1 范围内。而在现实中,相分数应该只存在两个数值:0 和1。这种计算方法中,0 <α <1 的情况会导致相界面模糊。为了使相界面更加清晰,采用OpenFOAM 开发的界面压缩方法对VOF模型进行了优化[18]。通过引入一个人工对流项对相界面处的相分数进行压缩,以限制这种界面模糊性。添加人工对流项后,式(9)可表示为
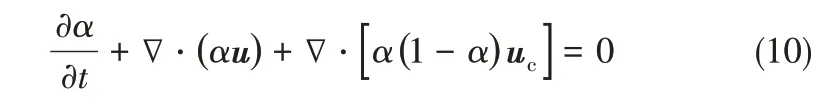
式(10)左边第三项即为人工添加的压缩项,在非界面处为0[19]。uc为需要模化的速度,为了不改变界面的位置,压缩效果只作用在界面的法向上,因此其方向与界面法向量同向,最大值不超过u。为了确保相界面位置不发生改变,Weller[20]提出uc可表示为
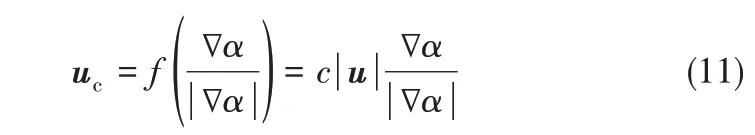
其中,c 为可控压缩因子,当c = 0 时无压缩效果,c 越大压缩效果越明显。本文选取c= 1 进行界面压缩。该方法相比传统的PLIC 等界面重构方法[21],可以节省更多的计算资源。
1.3 离散格式
模拟全部采用interFoam 求解器进行,压力-速度耦合采用PISO 算法。表1 列出了控制方程各项的离散格式。为了保证计算的稳定性和收敛性,模拟采用自适应时间步长,即在每次迭代开始时,根据库朗数计算一个新的时间步长。本研究设置模拟最大库朗数为0.5。
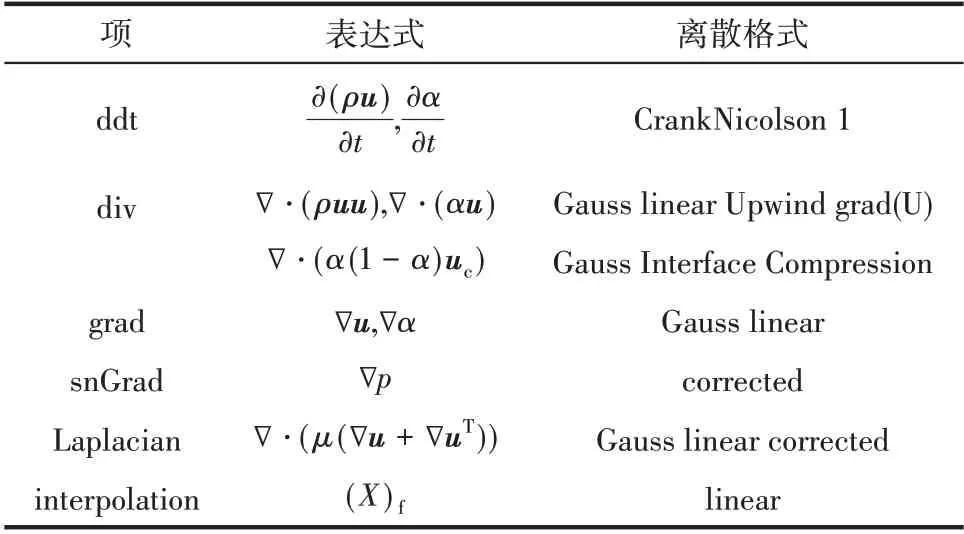
表1 方程各项离散格式Table 1 Discretization schemes for different terms of governing equations
2 模型构建
三维流动聚焦微通道的几何模型如图1 所示,通道截面为正方形,宽度为0.6 mm。为了保证流动在交叉处达到充分发展状态,采用式(12)计算了层流状态下的入口段长度[22]
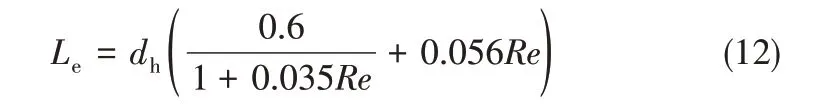
由于微通道特征尺寸较小,本研究中流动的Reynolds 数在10-2数量级,入口段长度约为通道水力直径的0.6 倍。因此,模型设置交叉口上游段长度为1.8 mm,下游段长度为18 mm。微通道内流动为典型层流流动,采用正方体网格对整个计算域进行离散。液滴的无量纲长度(液滴长度L 与通道宽度Wc的比值)随网格间距的变化如图2所示,当单个网格边长低于24 μm 时,进一步细化网格对计算结果基本无影响。
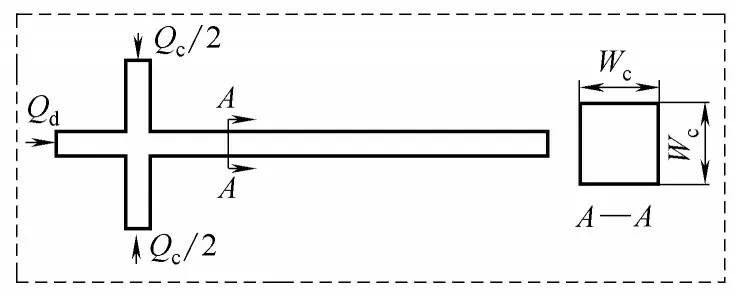
图1 流动聚焦型微通道几何模型Fig.1 Geometry of flow-focusing microchannel
离散相流体以恒定流率Qd从通道左侧流入,幂律剪切致稀流体作为连续相以Qc/2的流率从通道的两侧流入。模拟选取的流体属性如表2 所示,对于所有参数的幂律剪切致稀流体,流体黏度均随着剪切率的增大而减小。且在低剪切率下,黏度变化较大;在高剪切率下,黏度基本不发生改变。壁面采用无滑移边界条件,壁面处压力梯度为0,出口为大气压。
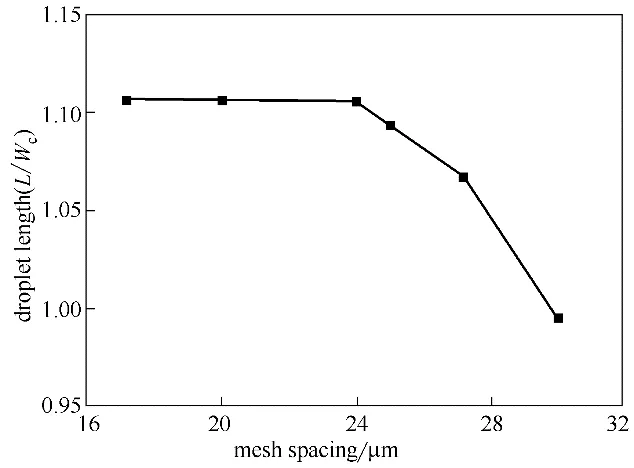
图2 网格独立性验证Fig.2 Mesh independence validation

表2 两相流体属性设置Table 2 Physical properties of two phases
3 结果与讨论
3.1 模型验证
3.1.1 VOF 模型验证 为验证interFoam 求解器的准确性,参考Fu 等[23]的微液滴破碎实验条件进行了数值模拟,液滴生成过程如图3 所示。离散相为硅油,连续相为去离子水,分别以Qd= 300 μl/min 和Qc=2000 μl/min的流率从通道入口流入。液滴的整个生成周期与脱离形态与实验结果基本一致。此外,在液滴脱离后的初始阶段均观察到了卫星液滴的存在,由于卫星液滴移动速度较快,在18 ms 左右与主液滴接触并融合。由于实验中各种不确定性因素的影响,如流体属性及流率的测量偏差、温度、壁面粗糙度及润湿特性等,计算结果和实验结果存在一定的偏差,且在微尺度条件下这些因素的影响更加显著。此外,拍摄条件也会对实验结果产生影响,当气泡移动速度较快且相机拍摄的快门速度不够时会造成拍摄所得的气泡图像周围存在一层拖影,从而造成拍摄到的尺寸大于实际气泡尺寸。对比实验和模拟结果,发现模拟得到液滴的移动速度稍大于测量值,这主要是实验中壁面摩擦力的存在造成的。
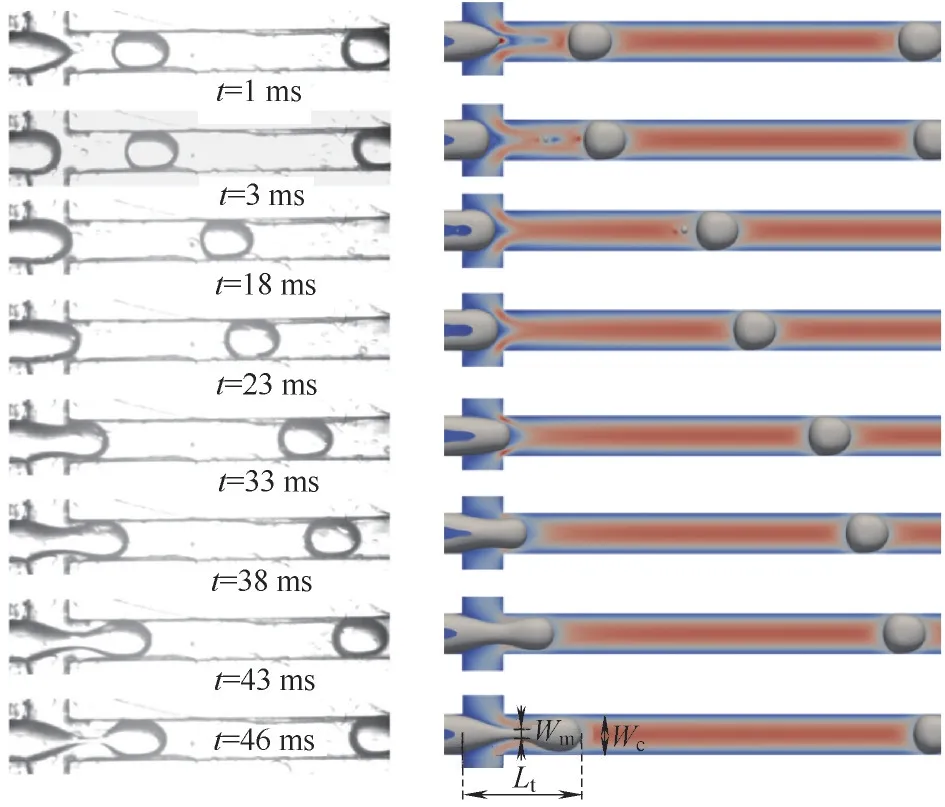
图3 液滴脱离过程中形态变化对比Fig.3 Comparison between calculated results and experimental data
液滴形成过程中两相不混溶线总长度Lt和颈部宽度Wm随时间的变化如图4 所示,在液滴生成过程的初始阶段Lt增长缓慢,随着时间的推移增长速度逐渐加快。总长度Lt的偏差主要受壁面润湿特性的影响,由于文献未给出壁面接触角,本文假设壁面被连续相完全润湿,造成破裂过程中总长度略小于实验测量值,壁面润湿特性对颈部宽度基本不会产生影响,因此模拟获得的颈部宽度数据与实验吻合较好。
3.1.2 幂律流体模型验证 为验证幂律流体模型的准确性,基于Fu 等[24]的实验条件,模拟了微通道内的幂律剪切致稀流体的单相流动。计算模型为正方形截面的直通道,截面边长为0.6 mm。流体采用0.1%(质量)的PAAm 水溶液,为典型的幂律剪切致稀流体,实验测得该流体的K 和n分别为0.35 Pa·sn和0.47。通道中部沿径向的速度大小如图5(a)所示,模拟结果与实验数据一致,说明该模型可以较好预测幂律流体在微通道内的流动状况。轴向截面的速度分布如图5(b)所示,流动主要集中在通道中央,壁面附近流速较小,由于边界层的存在,使壁面附近形成较大的速度梯度(剪切率),而在主流区速度梯度基本为0。由于该流体剪切致稀的性质会形成图5(c)所示的黏度分布,在壁面附近高剪切率区流体黏度较小,而在管道中央剪切率基本为零的区域会形成高流体黏度区。
3.2 液滴生成
3.2.1 液滴生成过程 根据瞬态形态的不同,整个液滴生成过程大致可分为三个阶段,如图6所示。
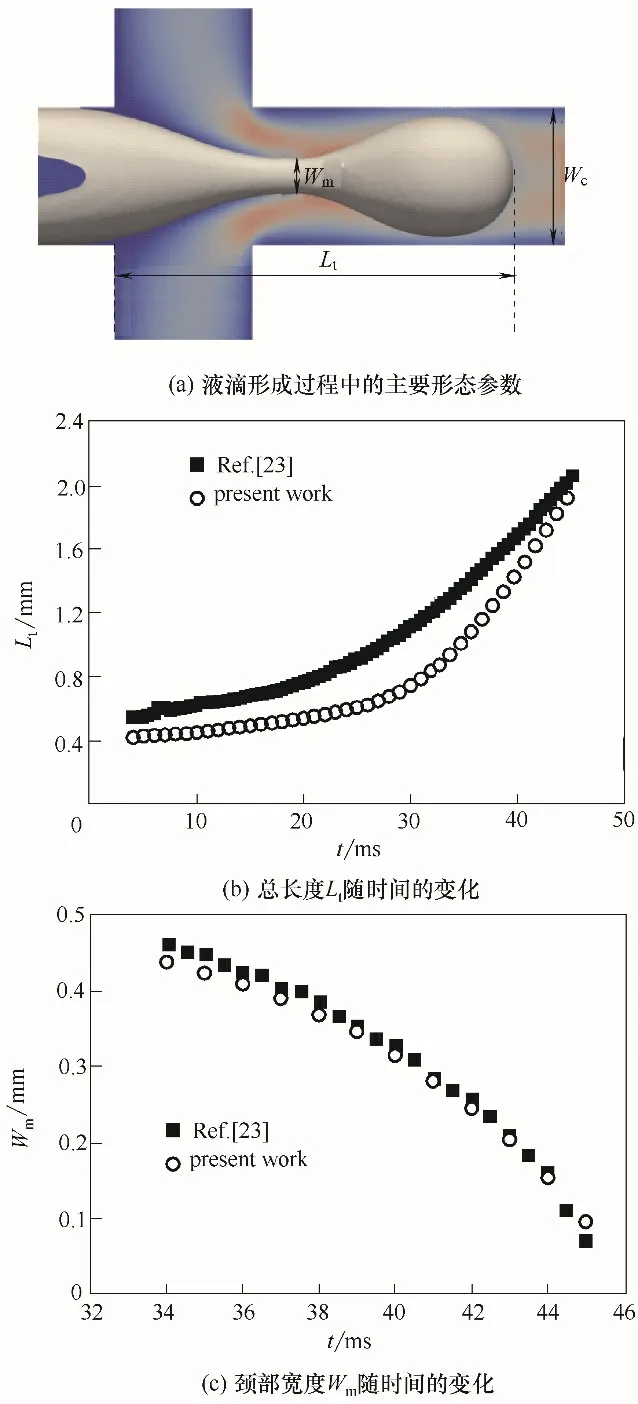
图4 液滴生成过程中主要形态参数的瞬态变化Fig.4 Temporal evolutions of thread tip and minimum width of thread neck during droplet formation process
(1)离散相流体在交叉口处成泡,并生长至颈部开始出现。由于界面张力的限制作用,该阶段的持续时间较长,约持续120 ms,占整个液滴生成周期的大部分。离散相在黏性剪切力的作用下会在界面附近形成两个轴对称的涡,促使液泡在交叉处继续膨胀。
(2)颈部快速收缩直至液滴发生断裂。此过程持续时间较短,从120 ms 开始约持续28 ms。该阶段内相界面处涡流现象消失,离散相头部达到与连续相相同的流速,但颈部会出现明显的速度梯度。其主要原因是当颈部出现后,颈部处的界面张力由限制作用转变为推动作用,结合流动压力和黏性剪切力促使液滴迅速生长脱离。
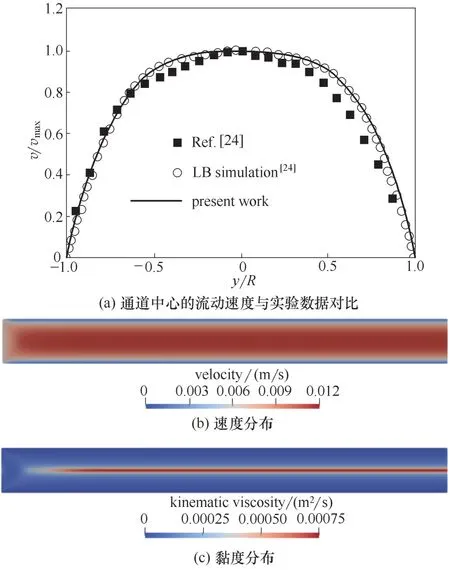
图5 微通道内速度及黏度分布状况Fig.5 Velocity and viscosity distribution in microchannel
(3)液滴断裂瞬间至第二个液泡开始生长,该过程持续时间极短,只有1 ms 左右。在界面张力的作用下,生成的液滴尾部和离散相前缘迅速收缩成半球状,达到平衡状态,此过程两相界面处仍保持较大速度,而后由于界面张力的阻碍作用,液泡内速度分布逐渐减小达到0 ms 时刻的状态,新的液滴在此基础上继续生成。
由于连续相压力、黏性剪切力和界面张力在液滴形成过程中作用程度的不同,会使液滴的破碎呈现挤压状、滴状和射流状三种不同的流型。在挤压状流型中,离散相会在膨胀阶段完全堵塞交叉结构,此时液滴破裂主要由连续相压力控制,受两相流率的影响较大。随着连续相流率或黏度的增大,作用在界面上的黏性剪切力增大,液滴破碎模式开始由挤压状向滴状转变。滴状破碎过程与挤压状类似,主要区别是,在滴状流型中液滴不会完全堵塞交叉口,液滴与壁面之间始终存在一层连续相液膜。因此,上游连续相压力的效果减小,液滴生成主要由黏性剪切力和界面张力控制,主要受连续相毛细数的影响。随着黏性剪切力的进一步增大,液滴破碎开始进入射流状流型,此时液滴破裂发生在交叉口下游,连续相压力在破碎过程中基本不起作用,离散相在黏性剪切力的作用下头部失稳并断裂成单分散液滴。
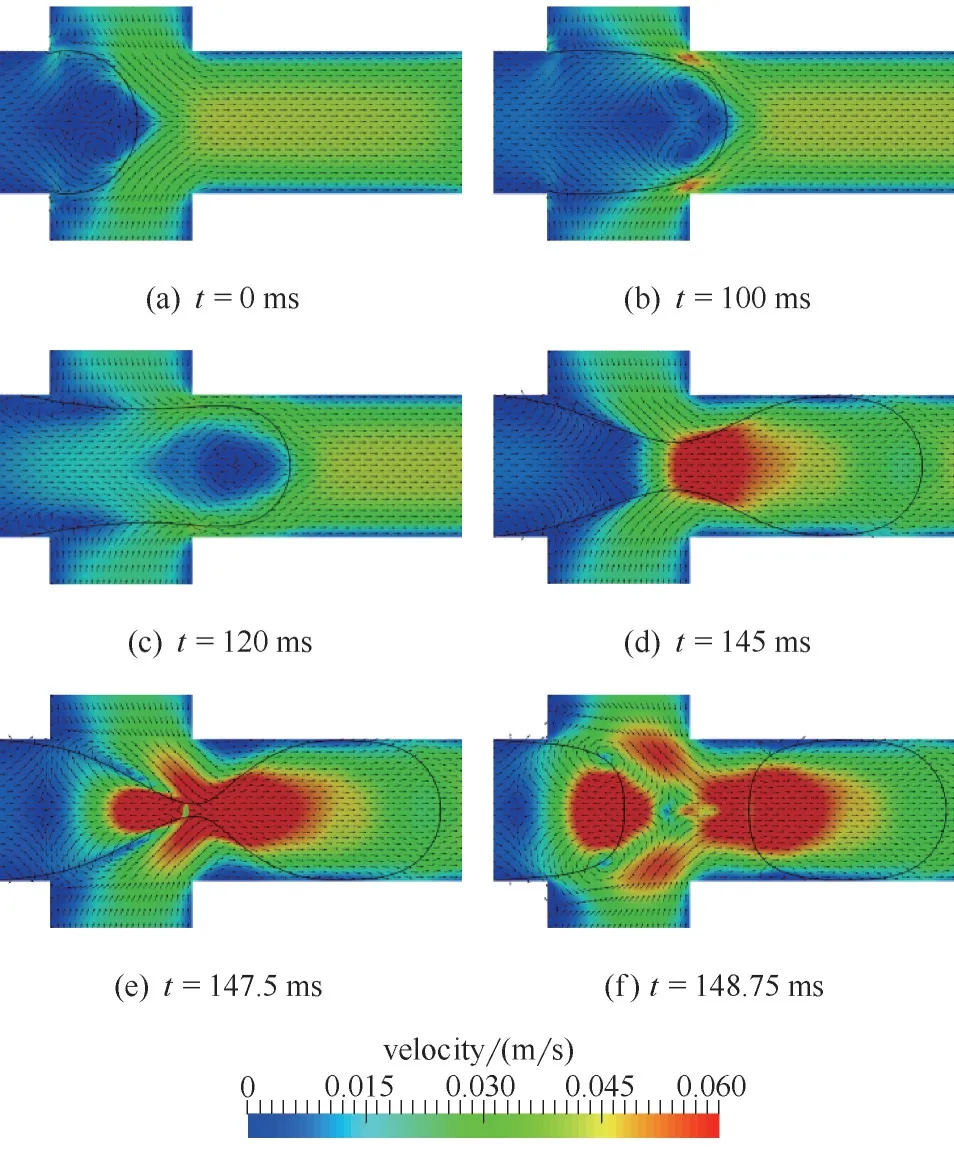
图6 液滴形成过程中速度分布(Qd=60 μl/min,Qc=480 μl/min,K=0.35 Pa·sn,n=0.47)Fig.6 Velocity distribution during droplet formation process
3.2.2 幂律指数的影响 模拟研究了幂律指数n对液滴生成过程、尺寸及频率的影响。微液滴生成过程中液泡长度Lt及颈部宽度Wm的变化如图7所示。图7(a)表明离散线在初始阶段受限于界面张力的作用生长缓慢,随时间保持近似线性关系。随着时间的发展,当颈部出现之后离散线开始迅速生长并断裂,长度呈现近似指数增长的趋势。此外,随着n 的增大,液泡演变周期T 逐渐减小。图7(b) 为颈部宽度的演变过程,表明颈部宽度Wm与周期内剩余时间T-t 呈幂律关系,其变化规律可表示为
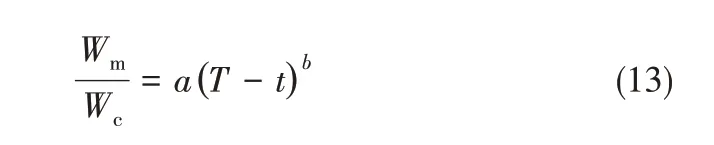
式中,a 和b 均为经验系数,与Fu 等[23]提出的微液滴在牛顿流体中生成时的颈部宽度变化规律一致。
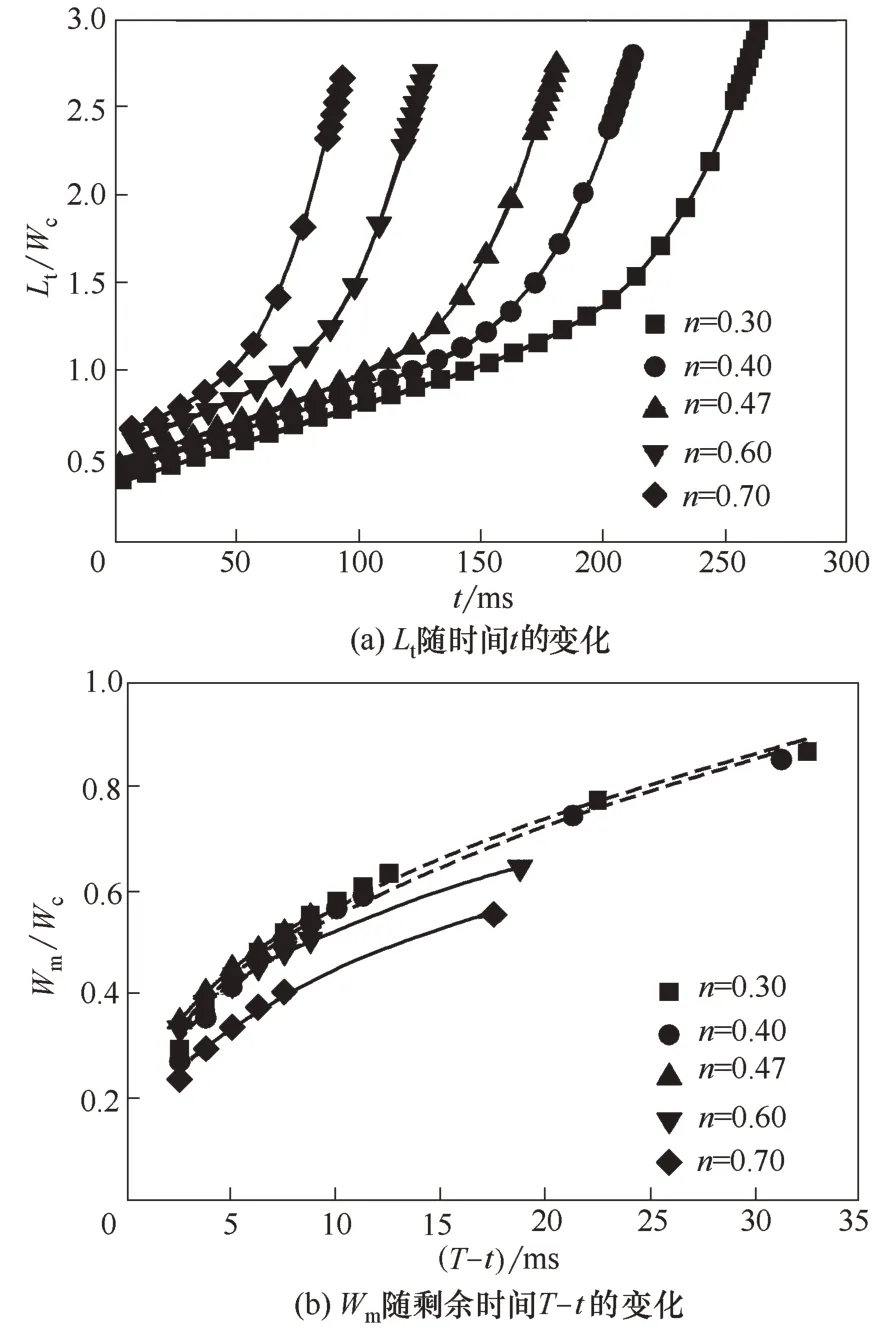
图7 不同n下不混溶线形态的变化过程(Qd=60 μl/min,Qc=480 μl/min,K=0.35 Pa·sn)Fig.7 Break-up dynamics of dispersed thread for various n
不同n的剪切致稀流体中微液滴的生成过程如图8所示,在其他条件不变的情况下,液滴的生成周期及大小均随着n 的增加而减小。主要原因是,连续相流体的有效黏度(μeff)随着n 的增加而增加,使作用在界面上的黏性剪切力更容易克服界面张力的限制,从而使液滴尺寸和生成时间减小。毛细数Ca 作为衡量黏性力与界面张力的无量纲数,表达式为

由于流动过程中非牛顿流体的黏度不稳定且不均匀,通过传统的计算方法无法得到Ca 的数值。因此,本文通过引入一个计算平均剪切率的方法来实现幂律流体Ca的计算[25]
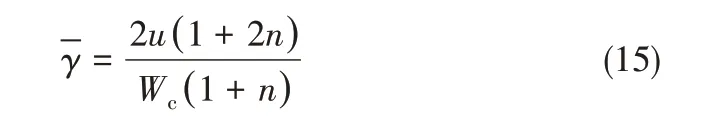
随着连续相Ca的增大,通道内的两相流型由挤压状转变为滴状,最终转化为射流状,与现有的研究一致。
图9(a)表明由于连续相有效黏度的增大,液滴的无量纲长度随n 的增大而减小。Sontti 等[14]和Shi等[15]模拟了T 型通道内牛顿微液滴在不同幂律流体中的生成过程,液滴大小随n的变化趋势相似,且都呈现线性变化。图9(b)表示液滴生成频率f 随n 的变化,随着n的增大液滴生成频率逐渐增大。
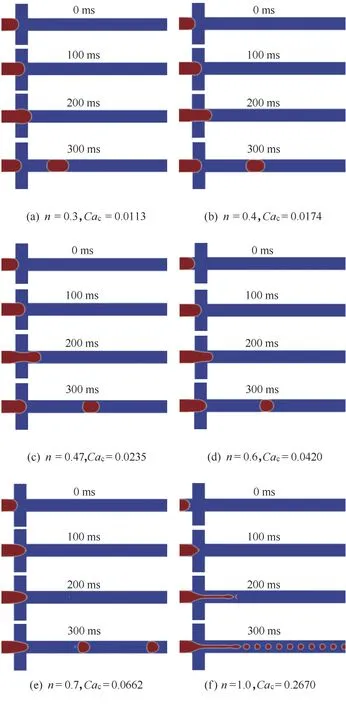
图8 不同n幂律流体中牛顿液滴的形成机制(Qd=60 μl/min,Qc=480 μl/min,K=0.35 Pa·sn)Fig.8 Newtonian droplet formation mechanism in power-law fluids with different n
3.2.3 稠度系数的影响 本文还研究了稠度系数K对液滴生成的影响。式(6)表明随着K 的增大,连续相流体黏度等比增大。Lt和Wm的变化如图10所示,相比n 的变化,K 的变化对生成周期的影响相对较小,且随着K 的增大,差距逐渐减小。图10(b)表明颈部宽度仍与(T-t)b呈正比,且当K和n改变时,b的变化范围不大。图11 为不同K 条件下单个液滴生成的演化过程,随着K的增大,液滴的大小和生成周期逐渐减小,液滴生成呈现更快更小的趋势。此外,随着K的进一步增大,流型也将由滴状向射流状转变。
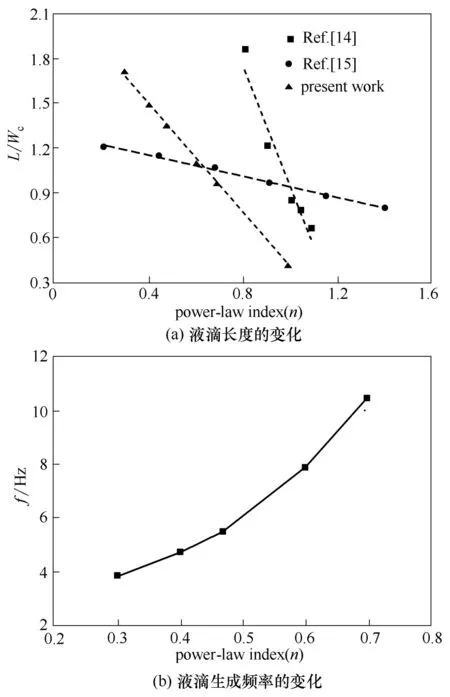
图9 液滴尺寸及生成频率随n的变化(Qd=60 μl/min,Qc=480 μl/min,K=0.35 Pa·sn)Fig.9 Variations of droplet size and formation frequency with n
微通道内的液滴生成过程可以看作一个半稳定过程,当离散相流率不变时单个液滴的体积V 与生成频率f的关系可以表示为

由于连续相黏度的增大,液滴尺寸随着K 的增大而减小,因此生成频率呈现逐渐增大的趋势,如图12所示。
液滴无量纲长度随连续相毛细数Cac的变化如图13 所示,液滴的长度与Cac呈现幂指数关系,与Fu等[26]的实验研究结果一致,将Shi等[15]的模拟数据按照该方式拟合可以得到同样的规律,该规律可用于液滴生成大小的简单预测。
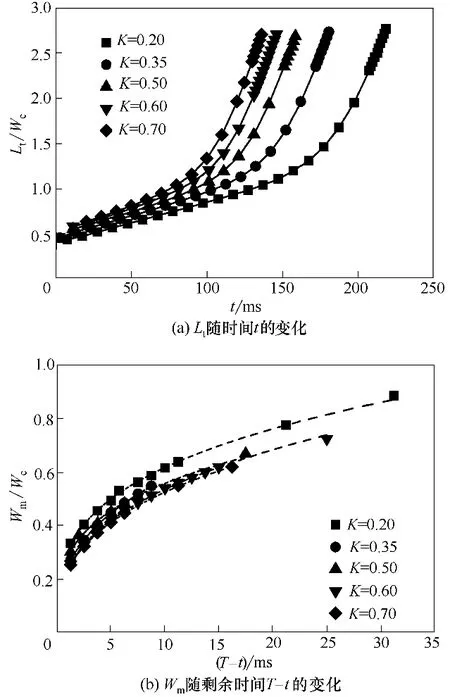
图10 不同K下不混溶线形态的变化过程(Qd=60 μl/min,Qc=480 μl/min,n=0.47)Fig.10 Break-up dynamics of dispersed thread for various K
4 结 论
本研究基于开源CFD 平台OpenFOAM,对流动聚焦微通道内非牛顿流体作为连续相的微液滴生成进行了数值模拟。首先,通过与实验数据对比验证了数值方法的可行性和准确性。然后,基于此验证,模拟了流动聚焦微通道内微液滴在幂律剪切致稀流体中的形成机理及行为,研究了稠度系数和幂律指数的影响。
通过与文献中的实验数据进行对比表明,interFoam 求解器对液滴在微通道内的生成和流动状况可以做出较好预测,证明该求解器可以用于模拟该尺度下微通道内的两相流动,且计算精度满足要求。此外,通过与非牛顿流体流动速度分布的实验数据对比,验证了幂律剪切致稀非牛顿流体模型用于计算微通道内非牛顿流体流动时的准确性。
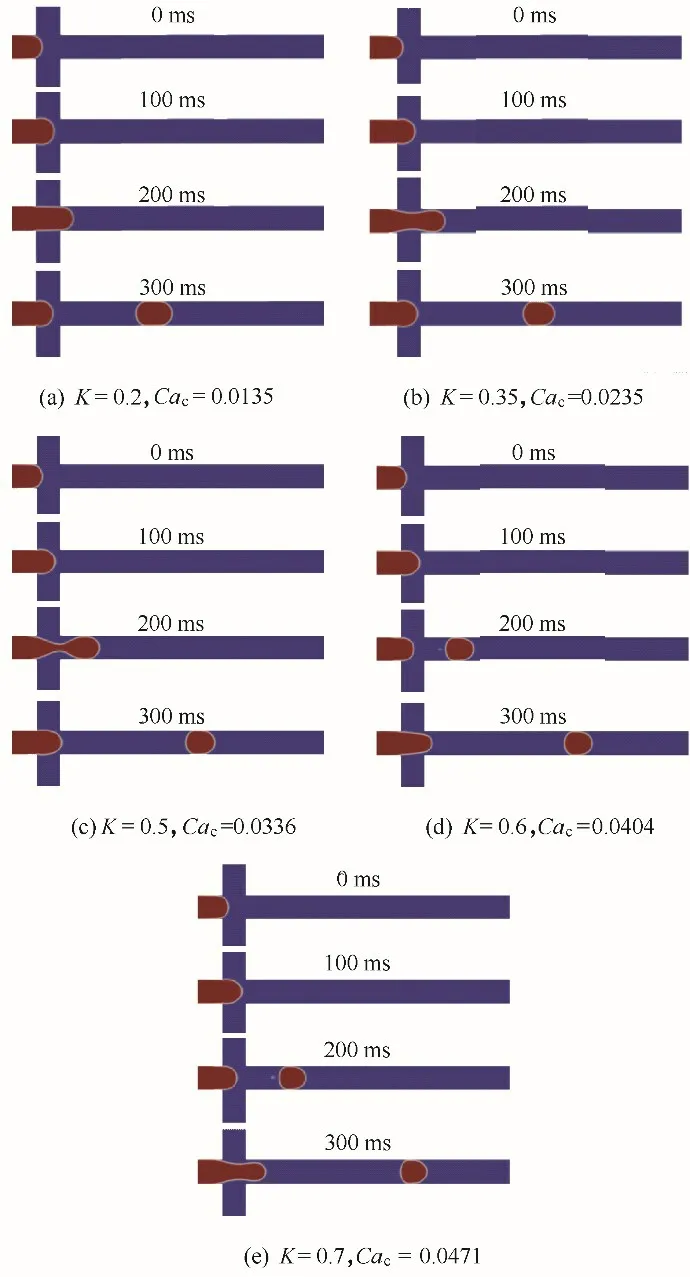
图11 不同K幂律流体中牛顿液滴的形成机制(Qd=60 μl/min,Qc=480 μl/min,n=0.47)Fig.11 Newtonian droplet formation mechanism in power-law fluids with different K
通过对幂律流体中微液滴生成过程的模拟研究表明,在液滴生成过程的初期,离散相颈部缓慢缩小;但后期在连续相压力和界面张力的共同作用下,液泡颈部迅速缩小并断裂。颈部宽度Wm与周期剩余时间(T-t)呈幂律关系。此外,在液滴生成的初期,液泡总长度Lt随时间缓慢增长,并与时间呈线性关系;在后期,由于界面张力方向的改变,液泡的总长度以类似指数函数的形式随时间迅速增长。
通过分别改变幂律连续相流体的K 和n,研究了它们对微液滴的尺寸和生成周期的影响。结果表明,液滴的尺寸随K 或n 的增大而减小,生成频率则随着两个值的增大而增大。相对于K 的变化,n的变化对液滴尺寸和生成周期的影响更加显著。随着K 和n 的增大,两相流型均呈现由挤压状向滴状进而向射流状的转变。此外,研究表明改变连续相的流变特性,液滴的长度与连续相毛细数呈幂律关系。
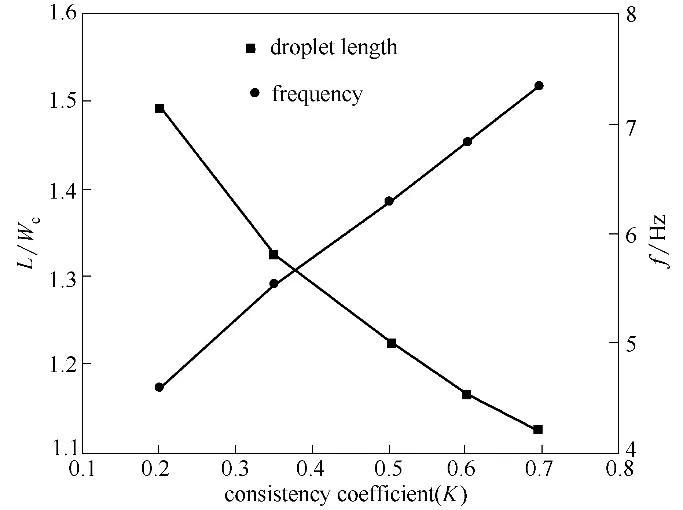
图12 液滴长度及生成频率随K的变化(Qd=60 μl/min,Qc=480 μl/min,n=0.47)Fig.12 Variations of droplet size and formation frequency with K
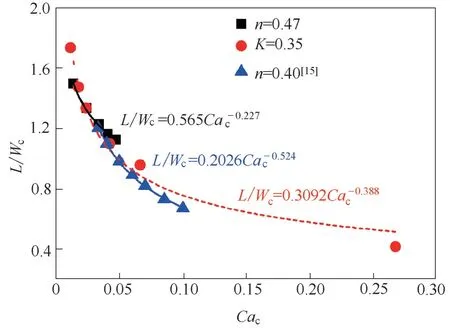
图13 液滴长度与连续相毛细数的关系Fig.13 Relationship between droplet length and capillary number of continuous phase
符 号 说 明
c——界面压缩模型中的可控压缩因子
dh——微通道水力直径,μm
Fs——体积表面张力,N/m3
f——液滴生成频率,Hz
g——重力加速度,m/s2
K——幂律非牛顿流体稠度系数,Pa·sn
L——生成液滴的长度,μm
Le——微通道入口段长度,μm
Lt——两相不混溶线总长度,μm
Mw——壁面附近界面的单位切向量
N——壁面附近网格单元的界面法向量
Nw——壁面附近界面的单位法向量
n——幂律非牛顿流体幂律指数
p——压力,Pa
Qc,Qd——分别为连续相和离散相入口流率,μl/min
Re——Reynolds数
T——单个液滴生成周期,ms
t——时间,ms
u——通道内流动速度大小,m/s
u——速度矢量,m/s
uc——界面压缩模型中需要模化的速度,m/s
V——单个液滴体积,μl
Wc——通道宽度,μm
Wm——不混溶离散相的颈部宽度,μm
α——相分数
γ——剪切率,s-1
-γ——剪切致稀非牛顿流体平均剪切率,s-1
θw——壁面处的静态接触角,(°)
κN——界面曲率
μ——动力黏度,Pa·s
μeff——非牛顿流体的有效黏度,Pa·s
ρ——流体密度,kg/m3
σ——界面张力系数,N/m
τ——剪切应力,N/m2
下角标
c——连续相
d——离散相
