双足爬壁机器人三维壁面环境全局路径规划
2020-12-21卢俊华朱海飞梁经伦管贻生
卢俊华,朱海飞,梁经伦,管贻生
(1. 广东工业大学 机电工程学院, 广州 510006; 2.东莞理工学院 机械工程学院,广东 东莞 523808)
随着城市建筑业和交通业的快速发展,人们希望用爬壁机器人辅助甚至代替工人来完成大型建筑如高楼、桥梁等的壁面清洁、检测和维护等高风险作业,提高作业的自动化程度和安全性.
路径规划是爬壁机器人自主执行作业任务必不可少的运动决策过程. 当前爬壁路径规划的研究主要围绕轮式和履带式爬壁机器人展开. 文献[1]用混合整数线性优化方法为爬壁机器人规划房间环境中的无碰路径. 文献[2]研究了爬壁机器人在圆柱形油罐壁面执行焊点检测作业的路径. 文献[3]用改进的神经网络模型求解能耗最小的壁面全覆盖路径. 该类方法适用于单一壁面或者相邻壁面相连的场景. 在多壁面组成的三维壁面环境中,若壁面之间并非直接相连通,轮式或履带式爬壁机器人将难以在壁面之间过渡并执行作业.
双足爬壁机器人拥有铰链式的关节主体和足式运动特性,能够跨越壁面障碍甚至在不同壁面间过渡,如ROMA II[4]、Crawler Robot[5]和CROC[6],更适用于三维壁面环境中的各种作业任务. 双足爬壁机器人路径规划方面的研究较少. 文献[7]着眼于每步运动的姿态安全性,用图搜索求解最优的附着点路径. 其他双足攀爬机器人(例如爬杆)路径规划方面,文献[8]从能耗最优的角度优化攀爬路径,文献[9]借鉴旅行商问题的思路,用图搜索规划节点路径,文献[10]则利用攀爬对象之间的过渡区域做路径规划. 在三维壁面环境的全局路径中,不同壁面间关键的过渡位置决定了全局路径的走向以及长度,而上述方法均未考虑关键过渡位置的求解.
在三维壁面环境中,全局路径必须分析爬壁机器人在不同壁面之间的可过渡性,为其在不同壁面间的过渡运动提供先验信息. 文献[11]研究步态和自由度对壁面可过渡性的影响,但并未考虑环境特征. 文献[12-14]从各种传感信息获取环境特征,再判断机器人能否过渡到下一个攀爬对象,但该方法只适用于实时和局部的过渡性分析,缺少全局观. 文献[15]从全局上根据杆件特征与机器人逆运动学之间的关系分析机器人在不同杆件间的可过渡性,但难以适用于壁面特征中.
综上,现有的方法均未能有效求解双足爬壁机器人在三维壁面环境的全局路径. 为此,本文提出了一种同时考虑壁面可过渡性和最优过渡落足点的规划方法, 分析壁面和机器人在壁面间过渡的可达工作空间的关系并对两者作简化,借此用几何图形的相交测试解决壁面可过渡性问题,降低工作空间的计算复杂度,并为全局壁面序列搜索提供过渡性拓扑地图. 另外本文还建立了优化数学模型求解机器人最优无碰壁面过渡落足点,获取最优全局路径. 该方法适用于双足爬壁机器人在复杂三维壁面环境的全局路径优化求解.
1 问题描述
1.1 双足爬壁机器人及其运动
双足爬壁机器人拥有多自由度的串联式关节主体与两个足式吸附末端,能够采用多种步态完成全向移动、避障、跨障和不同壁面间过渡等攀爬动作,一端吸附时另一端可自由运动,适合在多壁面组成的建筑环境中执行日常作业任务.
本文以自主研发的模块化双足爬壁机器人W-Climbot作为研究对象. W-Climbot及其构型示意图如图1所示. 其中间为3个摆转关节、两端再分别依次串接旋转关节和吸附末端,为5自由度对称式构型,便于运动规划与控制. 更多关于W-Climbot运动性能和运动步态等内容可参考文献[16].
1.2 壁面环境及其表达
在桥梁、展馆和歌剧院等大型建筑中,存在大量多幅壁面组成的“壁面环境”,如图 2(a)的桥梁钢梁外表面、图2(b)的玻璃幕墙等. 该类三维壁面环境有以下特点:1)壁面之间无法保证直接相连;2)壁面之间的相对位姿关系多样. 从图2中标注的实线多边形可见,壁面环境基本元素主要为有明确边界的空间平面.

图1 W-Climbot及其构型示意图

(a) 桥梁钢梁外表面 (b) 玻璃幕墙
不失一般性,本文使用凸多边形来表示壁面w(边界轮廓为凹多边形的,可以分割成有限个凸多边形[17]),有
w={pi|i=1,2,...,N,N≥3},
(1)

(2)
式中pn+1=p1,K表示空间中的任意一点. 进一步,用多个独立壁面wi的集合表示壁面环境,即
Ew={wi|i=1,2,...,Nw}.
(3)
式中,Nw表示壁面环境中的壁面数量. 为了研究方便,对壁面环境作出以下简化和约定:
1)壁面(凸多边形)之间可以在边界处交接,即有公共边,但不允许在壁面内部出现相互穿插的情况(该情况将处理成4个相互独立的壁面);
2)用壁面的法向量表示允许机器人攀爬的一侧;
3)全局路径不考虑机器人每一步的具体落足点和攀爬运动,因此不考虑壁面上的障碍物.
1.3 双足爬壁机器人全局路径描述
在三维壁面的攀爬环境中,双足爬壁机器人全局路径必须为机器人攀爬前进方向提供足够信息,发挥高效导向作用,包括:1)从起点到终点所经过的壁面及其次序,即全局壁面序列;2)全局壁面序列中每个壁面的第一个和最后一个落足点.Ns个壁面组成的全局壁面序列可表示如下:
(4)

(5)
式中:Q=(q1,q2,...,qNd)表示自由度为Nd的机器人各关节的关节变量,Qmax和Qmin分别表示关节变量的最大值和最小值. 相应地,双足爬壁机器人在三维壁面环境中的全局路径可表示如下:
(6)


图3 双足爬壁机器人的全局路径示意图
由图3可见,机器人有两条可行全局路径,分别对应全局壁面序列ws1=(w1,w2,w3,w4,w5)和ws2=(w1,w6,w5). 其中第一条全局路径为
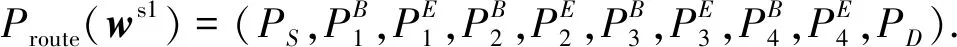
2 基于图形学的全局壁面序列规划
本文将机器人从一个壁面转移到另一个壁面的可行性定义为壁面可过渡性. 满足壁面可过渡性是全局壁面序列的硬性约束条件,直接关乎路径规划解的存在性.
2.1 壁面可过渡性分析流程
在满足机器人运动性能的前提下,双足爬壁机器人在两壁面之间的可过渡性和可达工作空间直接关联,即受机器人杆长、关节类型和关节运动范围影响. 当以其中一个壁面上的一点作为机器人的基座生成可达工作空间时,如果另一壁面处于可达工作空间内(满足位置和姿态可达),即表示机器人能在这两个壁面间执行过渡运动.
图4给出了壁面可过渡性分析的整个流程. 首先根据双足爬壁机器人过渡运动特点对两壁面作预处理:收缩和平移,以此简化机器人的可达工作空间. 分析机器人构型参数,用结构化的几何图形表示简化的可达工作空间. 然后取两多边形壁面边界的最近点对分别作为基座构建可达工作空间,并与非基座所在的壁面作相交测试. 一旦找到一个可达工作空间满足相交测试的点,则机器人可在该两壁面间过渡,否则不可过渡.

图4 壁面可过渡性分析流程图
2.2 壁面与可达工作空间简化处理
由于双足爬壁机器人多自由度和多关节类型的构型特点,求解其可达工作空间以及后续使用均过于繁琐. 结合机器人在壁面环境中的附着与过渡运动要求,可分别从姿态可达约束和位置可达约束考虑,先对壁面作预处理,消除姿态可达约束,从而简化机器人可达工作空间.
为了保证附着安全,双足爬壁机器人的末端吸附模块必须整体位于多边形壁面内部. 本文采用圆来表示末端吸附模块在壁面上的占位. 对壁面w采用收缩处理Sh(w,rm),收缩距离rm为圆的半径,末端吸附模块可简化成点,而有效可吸附壁面依然为凸多边形. 为了研究方便,下文中的壁面均已作收缩处理.
当双足爬壁机器人的两端在壁面附着时,一端作为基座,另一端作为吸附末端,两者坐标系的XOY平面必须与壁面平行,如图5(以W-Climbot构型为例)所示.
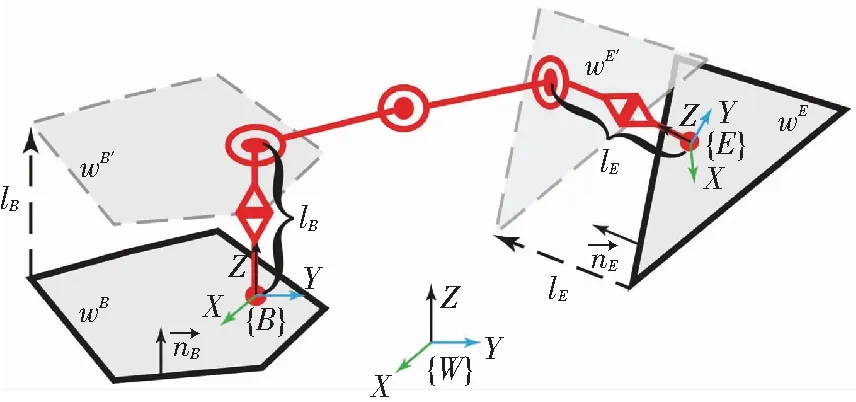
图5 壁面预处理示意图
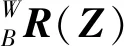
(7)

Tr(wB,wE,lB,lE).
(8)
式中lB和lE分别为沿着起始壁面和目标壁面法向,末端坐标系原点到距离最近的摆转关节的坐标系原点的距离(见图5). 由于旋转关节的旋转轴与连杆方向平行,所以该类关节的变化不改变连杆的长度. 该操作使双足爬壁机器人可达工作空间得到简化,不再与两末端连杆相关. 且简化后的可达工作空间与平移后的两个壁面wB′和wE′,只需满足位置可达的约束(相交)即表示机器人能在这两个壁面之间过渡.
2.3 机器人可达工作空间结构化表达
简化后的机器人可达工作空间可表示为
Ws(O,F),
(9)
式中O表示机器人基座,F表示机器人构型向量. 向量的参数与机器人构型相关,按构型的不同可分为两类:

(10)


(11)

图6 过渡运动时W-Climbot可达工作空间示意图
Fig.6 Schematic diagram of workspace for W-Climbot during transition
图6中: {B}和{E}表示过渡运动时的基座和末端目标点;{B′}表示平移后的基点,也是机器人可达工作空间的基座O;re是机器人中间两连杆的长度之和,即l2+l3.
2.4 基于几何相交测试的壁面可过渡性分析
对于给定的机器人构型参数以及壁面环境,式(10)中的F不变,所以可达工作空间和等效目标壁面的相交测试结果主要取决于机器人基座的位置. 双足爬壁机器人在两个壁面之间可过渡的条件可表示为
∃O∈wB′,Ws(O,F)∩wE′≠φ.
(12)
壁面上具有无限个点,显然不可能遍历所有点作为基座来测试,本文选取两壁面的最近点作为关键点. 由计算几何知,存在两凸多边形距离最小的一对点,其中一个点在所属壁面的边界上. 因此,在壁面平移后的基础上求解两壁面的边界最近点对,分别取点对中的一点作为基座构建可达工作空间,并与另一壁面作相交测试. 一旦找到一个可达工作空间满足相交测试的点,则两壁面可过渡. 设两壁面分别有N1和N2条边界,则边界最近点对有N1×N2对. 分析过程可表示为
(13)
式中min(ei,ej)表示边界ei和ej的最近点对. 由于两壁面都可能为起始壁面,且两壁面的可过渡性是相互的,所以必须考虑两个壁面的边界点.
需要注意的是:本文所提出的壁面可过渡性分析方法只从机器人可达工作空间考虑,尚未严格计算关节运动范围约束与无碰约束,所以该方法属于必要非充分条件,适用于快速筛选. 关节运动范围约束和无碰约束将在第3节中考虑和分析.
2.5 基于图搜索的全局壁面序列搜索
壁面可过渡性分析完成后,通过拓扑地图来表示不同壁面之间的过渡性:一个节点表示一个单独的壁面,节点之间用边连接来表示壁面之间可过渡. 然后,采用深度优先的图搜索方法来搜索从起点所在壁面到终点所在壁面的全局壁面序列. 由于图搜索的对象为壁面环境的过渡性拓扑地图,最大程度上消去了其他无影响因素,于是该方法能快速求解环境中所有全局壁面序列,具体实现可参考文献[15].
3 过渡落足点序列全局规划与优化
对壁面环境中全局壁面序列的路径走向添加约束和优化目标,赋予其量化的评价指标,进一步对全局壁面序列作筛选与优化,将全局路径求解结果最优化.
于是,对图搜索得到的全局壁面序列分别求解相邻壁面间的最优过渡落足点,获得可行的全局路径规划结果并选择最优者. 以全局路径长度最短为优化目标,以过渡落足点的位置、运动学和对应的位形无碰为约束,建立非线性优化数学模型求解壁面过渡落足点. 以下是落足点序列最优化问题的数学描述:
1)过渡落足点位置约束. 过渡落足点必须位于凸多边形壁面内部,可得:1)过渡落足点必须在多边形所在的平面上;2)当按同一旋转方向遍历多边形所有边时,过渡吸附点应在所有边的同一侧. 约束表达式如下:
(14)
(15)
2)壁面过渡运动学约束. 双足爬壁机器人在两个壁面间执行过渡运动时需满足机器人运动学约束,包括位置可达、姿态可达约束和关节运动范围约束,即式(5)和式(7).
3)壁面过渡无碰约束. 执行壁面过渡运动时,还要求机器人与三维壁面环境无碰撞. 该无碰约束可表达为
Li∩wB=φ,i=2~Nl,
(16)
Li∩wE=φ,i=1~Nl-1.
(17)
其中Li表示机器人从基座到吸附末端顺序的第i根连杆,Nl表示连杆数目. 式(16)表示第2根连杆到最后一根连杆与起始壁面无碰,式(17)表示第1根连杆到倒数第2根连杆与目标壁面无碰. 双足爬壁机器人与壁面的碰撞分析可以通过将机器人连杆简化成空间线段,再求出空间线段与凸多边形壁面的距离,然后与安全距离作比较[18].
4)优化目标及数学模型表达. 过渡落足点优化求解的目标是所有落足点构成的全局路径最短,目标函数为
(18)
式中Ns表示全局壁面序列中的壁面数量,需要执行Ns-1次过渡运动,对应的壁面过渡落足点数量是2Ns-2,每次过渡运动都必须符合上述三种约束. 最终过渡落足点优化求解的数学模型表示如下:
(19)
4 仿真与分析
以W-Climbt为研究对象,在Visual Studio和MATLAB平台搭建仿真环境并进行仿真验证. 仿真程序在台式计算机上运行,硬件配置为Intel i7-7700,3.6 Ghz,内存8 G.
4.1 全局壁面序列规划仿真结果
随机生成多个壁面组成三维壁面环境,给各个壁面编号并用箭头表示可攀爬的一侧,且随机设置路径起点和终点. 取其中3个壁面环境作为测试案例:案例1由5个壁面组成,壁面3和壁面2分别为起点和终点所在壁面;案例2由5个壁面组成,壁面1和壁面2分别为起点和终点所在壁面;案例3由10个壁面组成,壁面7和壁面2分别为起点和终点所在壁面.
首先对壁面环境中每两个壁面做可过渡性分析,然后搜索全局壁面序列. 仿真运行后,在测试案例1、2和3中分别得到1条、2条和2条全局壁面序列. 3个测试案例的计算时间均只需要1 ms. 为了进一步分析该过程的算法计算效率,分别在5至20个壁面组成的多个壁面环境中求解壁面可过渡性和全局壁面序列,算法的平均运行时间仅为2 ms.
4.2 过渡落足点优化求解仿真结果及比较
将过渡落足点优化求解的数学模型解析成通用的优化算法,只需输入全局壁面序列与机器人构型参数即可求解出优化结果. 结合MATLAB优化工具箱中的非线性优化求解工具fmincon,对上述3个测试案例的全局壁面序列求解最优过渡落足点.
图7~9展示了壁面环境和机器人全局攀爬路径. 起点、过渡落足点和终点依次连接组成全局路径,路径中的箭头表示前进方向. 全局壁面序列中的壁面用直线边界显示,其他壁面用虚线边界显示. 根据相邻壁面间的过渡落足点生成W-Climbot过渡运动位形,验证求解的过渡落足点是否有效. 图7所示为案例1中全局壁面序列3→1→4→2的全局路径,路径长度为6.740 m,耗时1.87 s. 图8为案例2中全局壁面序列1→3→4→2的全局路径,路径长度为6.018 m,耗时2.07 s;另一全局壁面序列1→2由于不能满足机器人与壁面的无碰约束没有得到优化解. 图9(a)为案例3中全局壁面序列7→6→5→3→2的全局路径,路径长度为16.106 m,耗时3.52 s;图9(b)为案例3中全局壁面序列7→6→5→9→10→2的全局路径,路径长度为25.582 m,耗时4.73 s,可知案例3中第一条全局路径是最优结果.

图7 测试案例1中优化的全局路径

图8 测试案例2中优化的全局路径

(a) 全局壁面序列7→6→5→3→2的最优全局路径

(b) 全局壁面序列7→6→5→9→10→2的最优全局路径
对不同全局壁面序列求解最优过渡落足点,分析该数学模型的有效性和求解时间. 运行120次案例求解,成功获得优化结果的次数为114,占比95%. 正如2.4节中所述,壁面可过渡性分析时由于基座未定因而无法考虑关节运动范围和无碰约束,而在过渡落足点优化求解时加入了上述约束. 当过渡运动不能满足上述约束时,求解器无法找到可行解,可进一步排除不可行的壁面序列.
通过案例分析发现求解耗时主要和全局壁面序列中的壁面数量有关. 表1给出了案例求解耗时的统计结果,可见全局壁面序列中的壁面数量越多,则求解耗时越长,并且增长的比例越大.
表1 不同攀爬壁面数量下的过渡落足点求解时间比较
Tab.1 Comparison of time consumption for solving transition adhering points with different numbers of climbing walls

全局壁面序列的壁面数量最大求解时间/s最小求解时间/s平均求解时间/s20.380.080.1831.030.210.5742.230.521.3054.710.702.3664.741.363.34
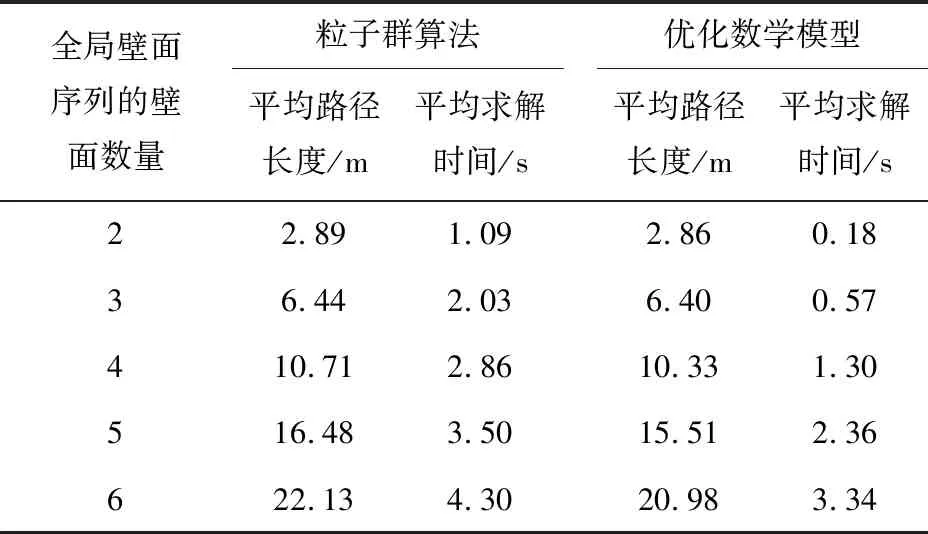
为进一步验证该优化求解算法的性能,将其求解结果与智能优化算法中的粒子群算法求解结果作比较. 在经过的壁面数量不同的情况下,两种算法求解的平均路径长度和平均耗时结果如表2所示. 为保证优化性能,粒子群算法中取粒子样本数目为50,迭代次数为200. 比较求解结果可知本文采用的优化数学模型求解方法平均耗时更少,且求得的路径平均长度更短,因此该方法具有更优的求解性能.
表2 优化数学模型和粒子群算法求解结果比较
Tab.2 Comparison of solving results between mathematical model and particle swarm algorithm
全局壁面序列的壁面数量粒子群算法平均路径长度/m平均求解时间/s优化数学模型平均路径长度/m平均求解时间/s22.891.092.860.1836.442.036.400.57410.712.8610.331.30516.483.5015.512.36622.134.3020.983.34
5 结 论
为求解双足爬壁机器人在三维壁面环境中的全局路径,本文从全局壁面序列和过渡落足点出发,提出了一种通用的最优全局路径规划方法. 运用图形学的思想分析机器人过渡运动中可达工作空间和壁面的关系,对两者建立结构化的数学模型,以此通过几何相交测试求解壁面可过渡性. 根据求解结果建立可过渡性拓扑地图,并应用图搜索快速获取机器人路径全局性的壁面序列. 该方法避免了对机器人复杂工作空间的直接求解,大大提高计算效率,仿真结果表明在5至20个壁面构成的环境中,平均求解时间只需2 ms. 本文还建立了过渡落足点优化求解的数学模型,该模型能有效求解路径最短的无碰过渡落足点,并对全局壁面序列作筛选和最优化,获得最优全局路径. 仿真结果表明获得优化结果的比例为95%,平均耗时均在4 s内. 该方法能为双足爬壁机器人在壁面上的局部运动路径求解提供最优输入,解决机器人自主作业路径的全局最优问题.
下一步工作将寻找性能更好的非线性优化求解器,提高过渡落足点求解的效率;并着手双足爬壁机器人的局部路径求解,研究其在壁面上克服障碍物的无碰落足点规划和单步无碰攀爬运动规划,做机器人实际攀爬实验.
