局部几何构型对聚焦流微通道内液滴生成特性的影响

宋祺，杨智，陈颖，罗向龙，陈健勇，梁颖宗

（广东工业大学材料与能源学院，广东广州510006）

引 言

液滴微流控技术是在微流控芯片基础上发展起来的一种全新操纵微小液体体积的技术，该技术主要利用流动剪切力与表面张力之间的相互作用将连续流体分割分离成离散的纳升级及以下体积的液滴[1]。与连续流技术相比，该技术具有诸多优点，如液滴体积小、试剂消耗减少、液滴样品间无扩散、反应环境稳定、可避免样品间的交叉污染等。因此，其在化学[2-7]、药学[8-13]和生命科学[14-15]等诸多领域得到了广泛应用。液滴微流控技术的核心是对微液滴的精确操控，而微液滴的生成是精确操控微液滴的前提。常见的生成微液滴的方式主要包括T型[16-18]、Y 型[19-22]、十字聚焦型[23-26]及同轴流[27-28]等微通道结构。与其他结构相比，十字聚焦型微通道内的液滴生成更易控制，液滴生成相对稳定、高效、均一度好，且液滴尺寸可调范围更大，因此受到广泛关注。

近些年来，针对十字聚焦微流控通道，不同学者基于实验和数值模拟方法，分别研究了两相流体物性（如表面张力、黏性系数）、流量比和通道几何结构等参数对液滴生成的影响，并建立了一系列用于预测液滴生成尺寸的关联式。Peng等[29]基于实验和模拟方法的研究发现：随表面张力的增大，液滴尺寸不断增大，生成频率不断降低。Wu 等[30]利用VOF 方法模拟研究了流动聚焦微通道下游局部孔口结构对液滴尺寸、单分散性和液滴生成频率的影响，发现液滴生成受孔口半径的影响较大，而对孔口长度不敏感。此外，液滴生成频率并不简单地随孔口半径呈单调性变化，而是当孔口无量纲半径*= 0.625 时达到最大值。Liu 等[31]利用格子Boltzmann 模拟方法研究了流量比、毛细管数和通道几何形状（宽度和深度）对液滴生成的影响，发现柱塞状液滴长度与流量比呈线性关系，与毛细管数呈幂律函数关系，并提出了一种基于流体流量和通道几何参数来关联液滴长度的数学模型。Tan 等[32]采用实验和数值模拟的方法，研究了下游主通道几何形状对液滴生成的影响，发现锥形扩张的几何形状有助于形成速度梯度，进而可实现液滴破裂位置的精确控制。Lashkaripour 等[33]针对具有下游扩张孔口的十字聚焦微通道，采用有限元模拟方法研究了液滴半径随流量比和毛细数的变化，发现毛细数和流量是影响液滴生成半径的主要因素。Gupta 等[34]针对聚焦流通道，采用格子Boltzmann 方法模拟研究了低毛细数下孔口宽度、孔口长度和孔口入口距离对液滴形成机制和液滴生成大小的影响，发现聚焦型通道内液滴的挤压阶段比T 型通道更早开始，液滴尺寸随孔口宽度和入口距离的增加而增加，而随着孔口长度的增加，呈先减小后增大的变化趋势。

综上所述，目前有关十字聚焦微通道内液滴生成的研究主要聚焦于流量比、毛细管数、表面张力等流体的流动和物性参数，以及通道几何结构参数，主要包含通道深度、下游孔口半径、形状和长度等对液滴生成特性的影响。此外，许多研究者在实验中通常经验上将分散相入口通过拉丝处理形塑成锥形结构[35-38]，以更好地实现液滴的可控制备。可见，目前文献中仍少有分散相入口通道结构及其与下游孔口协同对液滴生成特性的影响的相关报道。在模拟方面，目前针对多相自由表面流的模拟主要有拉格朗日式的界面追踪法（interface tracking）和欧拉式的界面捕捉法（interface capturing）。界面追踪法直接通过标记点跟踪界面的运动，如边界积分法（BIM）[39-40]、有限元法（FEM）[41]和浸没边界法（IBM）[42]等；界面捕捉法则根据描述界面物理量的演化来间接模拟界面的运动，如紧致插值曲线法（CIP）[43]、水 平 集 方 法（level set）[44]，流 体 体 积 法（VOF）[45]等。尽管界面跟踪法可实现对短暂的液滴破裂或融合过程的精确模拟，但对液滴破裂或融合之前或之后的动力学过程模拟比较困难[46]。相比于界面跟踪法，界面捕捉法则无须频繁对网格进行切割联通操作。微通道内的液滴生成过程不仅包含界面的变形和破裂，还包含界面的流动，这使得界面捕捉法成为实现该模拟的最好方法之一。在界面捕捉法中，流体体积法（VOF）和水平集方法（level set method）具有广泛应用，且在处理界面拓扑结构的变化方面优势显著[45-47]。其中VOF 方法具有良好的质量守恒性和简单的界面拓扑处理，但由于该方法的体积分数是一个阶跃函数，故很难获得精确的曲率和光滑的界面物理性质[48-49]。而level set方法不需要重构界面，可以隐式地捕捉界面且函数始终是光滑的，易于处理复杂界面变形或拓扑结构改变；但该方法的对流方程不是基于保守形式，故存在质量损失的缺点[50-51]。为了克服它们各自的缺点，Sussman 等[52]提出了一种新的VOF 与level set 耦合方法。目前该方法已成功地应用于微通道中两相流的模拟，并取得了较好的数值计算结果[53-55]。因此，本文将主要采用VOF/CSF 耦合level set 的数值模拟方法，深入研究分散相入口、下游通道孔口以及二者协同变化对液滴生成特性的影响，进而为十字聚焦通道内微液滴的生成特性提供更多的规律性认识，从而为后续实现液滴的精确调控提供重要指导。

1 几何建模

图1 为十字聚焦微通道的二维几何结构，其中两相入口夹角θ=90°，连续相和分散相入口段通道宽度为wc=wd=100 μm，两相交汇处下游的孔口宽度和长度为wori= Lori= 50 μm。为保证两相流动在下游微通道内充分发展，本文将出口段主通道宽度设为wo=100 μm，长度设为Lo=1250 μm。此外，本文选取硅油为连续相（其密度和黏性系数为ρc=965 kg/m3，μc=50 mPa·s），水为分散相（其密度和黏性系数为ρd= 998.2 kg/m3，μd= 1.005 mPa·s），两相间表面张力系数为σ=30 mN/m。为确保不同结构通道内均有液滴生成，经过多次实验，将连续相和分散相入口流速分别设定为vc= 0.03 m/s，vd= 0.05 m/s。

2 数学模型和可行性验证

2.1 数学模型

假定两相流体的密度和黏度为常数，因此可视为不可压缩的各向同性牛顿流体，故描述其动量守恒的Navier-Stokes方程控制方程如下所示

图1 十字聚焦微通道二维几何结构（下角标c和d分别表示连续相和分散相）Fig.1 Schematic diagram of 2D geometric structure of crossfocusing microchannel（subscripts c and d represent continuous and dispersed phase,respectively）

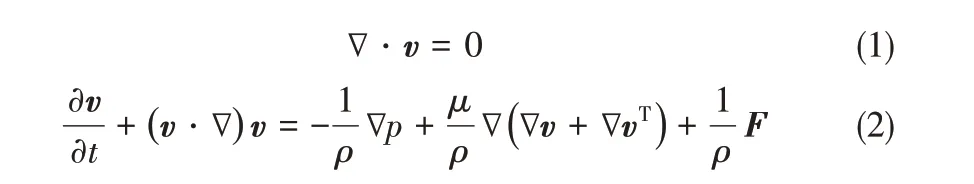
式中，v 是流体的速度矢量；t 是时间；p 为压力；ρ 和μ 分别是流体的密度和动力学黏度；(v·∇)v 为单位体积流体的惯性力；∇p 是单位体积流体所受的压强梯度；μ∇(∇v + ∇vT)表示单位体积流体受的黏性力；F 为与表面张力相关的动量源项。

由于微通道内液滴的形成涉及复杂的界面演变过程，如生长、挤压、破裂等过程，因此本文采用流体体积耦合水平集(VOF/CSF+level set)的界面显示算法对两相非混合界面进行捕捉。VOF 方法是通过计算每一个控制体积内连续相和分散相的体积分数来表征界面，如式（3）所示，其中κ 是界面曲率。假设计算的每个控制体积中分散相的体积分数为α，α = 1，表示该控制体内只含有分散相；α =0，则表示该控制体内不含分散相；0 ＜α ＜1，表示该控制体内有两相交界面。在混合控制体积内，式（1）和式（2）中的两相混合密度和黏度的计算可由式（4）和式（5）计算得到

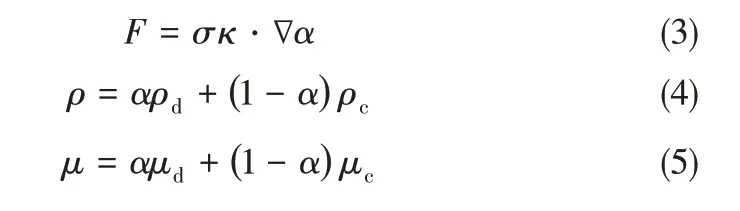
此外，每个控制体积内的体积分数α 可以通过求解一个（或多个）相的体积分数的连续性方程得到，如式（6）所示

level set 方法是把随时间运动的物质界面看作某个函数φ(x,t)的零等值面，即在每个时刻t，只要求出函数的值就可知道其零等值面位置，也即运动界面位置。构造函数φ(x,t)，使得在任意时刻，运动界面Γ(t) 恰好是φ(x,t) 的零等值面，即Γ(t) ={x ∈Ω:φ(x,t)= 0}，这里要求φ(x,t)的初值满足在Γ(t)附近为法向单调，在Γ(t)上为0, φ(x,0)取为x点到界面的符号距离函数，函数如式（7）所示

其中，d(x,Γ(0)) 表示x 到Γ(0)的距离函数；Ω1和Ω2分别表示第一种介质和第二种介质所在区域。由于在任意时刻t，φ(x,t)的零等值面就是活动界面，即Γ(t) = φ(x,t) = 0，所以函数φ(x,t) 应满足式（8）

在十字聚焦微通道内流体Reynolds 数较小，因此采用层流模型。连续相和分散相的入口由体积分数定义，两相入口速度均由常规速度定义，出口设定为具有101.325 kPa 的开口边界条件。通道壁面设定为无滑移边界条件。为了符合实验中芯片材料PDMS 通道壁面的疏水特性，防止分散相浸润通道壁面并保证液滴顺利生成，本文将接触角设定为135°。在Navier-Stokes 方程的数值求解中，采用SIMPLE 算法建立压力速度耦合，选用PRESTO！算法为压力插值方案。梯度计算采用least square cell based 方法，动量方程的空间离散化采用second order upwind，时间离散方式采用first order implicit。对于两相界面附近的控制体积，选用geo-reconstruct用于界面插值。

2.2 网格无关性和可行性验证

基于有限体积法（FVM）的数值模拟是基于网格进行迭代计算。通常在一定范围内，网格越小，计算结果越精确；但网格越小，所消耗计算资源越大。为寻求最具经济性的网格尺寸，本文采用四边形结构化网格对十字聚焦通道的二维几何模型进行网格划分（图2），分别选取了6 种尺寸(3 μm × 3 μm、2.5 μm× 3 μm、2 μm× 3 μm、2 μm× 2.5 μm、2 μm× 2 μm、2μm × 1.5 μm) 的网格单元来进行网格无关性验证，结果如图3 所示。当网格单元尺寸分别为2μm × 2 μm 和2 μm× 1.5 μm 时，液滴生成周期无明显差异，可视为网格大小对模拟结果的影响近似收敛。因此，为兼顾计算结果的准确性和计算成本，后续模拟中的几何通道均选用2 μm× 2 μm网格单元进行网格划分。

图2 数值模拟过程中网格无关性验证Fig.2 Grid independence validation

图3 不同网格所对应的液滴生成周期Fig.3 Droplet generation cycles for different grids

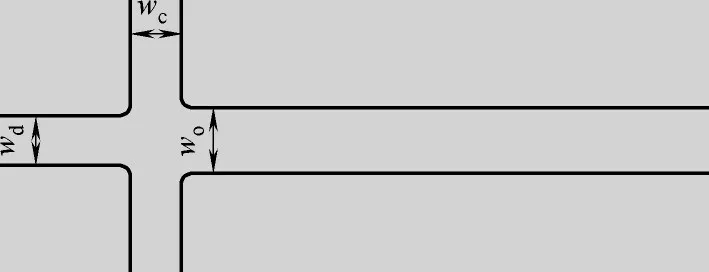
图4 实验通道结构Fig.4 Schematic diagram of experimental channel structure

此外，为验证模拟方法的可行性，模拟条件的设置与实验相同，即两相入口宽度均为wc= wd=100 μm，出口段主通道宽度为wo= 130 μm，如图4所示，连续相和分散性流量分别为Qc= 120 μl/h，Qd=60 μl/h，实验中十字聚焦通道内生成的液滴采用高速摄像仪进行拍摄，进而将模拟与实验结果在相同尺度下进行对比，如图5(a)、(b)所示。可见，实验获取的分散相液滴曲率和模拟获得的曲率极为相近。为了进一步验证模拟方法的可行性，本文固定分散相流量Qd=50 μl/h，将连续相流量从20 μl/h逐渐增大到70 μl/h，并将模拟和实验所获得的液滴直径进行对比，如图5(c)所示。考虑到实验通道壁面亲疏水特性不均一及两相在聚焦前存在的动量损耗等原因，模拟与实验结果总体上具有较好的一致性。

图5 液滴生成的模拟与实验结果对比Fig.5 Comparison of droplet morphology between simulation and experiment

3 结果与讨论

3.1 孔口宽度对液滴生成的影响

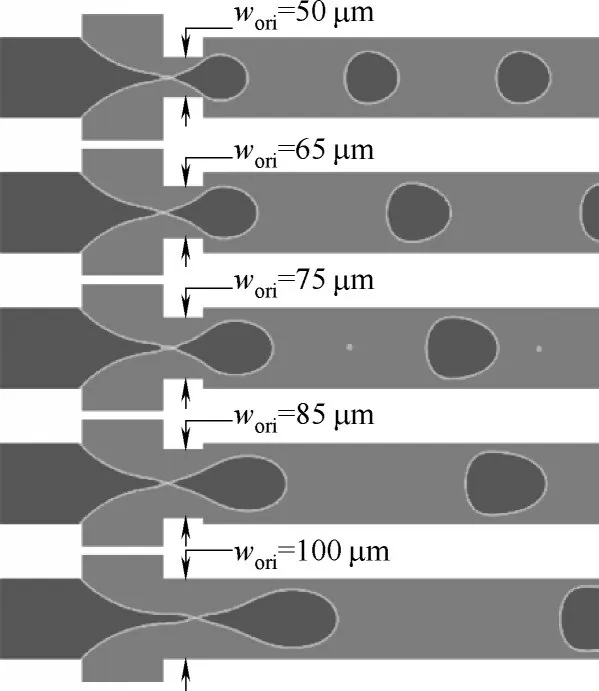
图6 不同孔口宽度下液滴断裂时刻的两相云图Fig.6 Two-phase cloud diagrams at droplet break-up under different orifice widths

分散相和连续相入口通道夹角θ=90°，孔口长度Lori= 50 μm，其他参数与图1 设置相同。为研究孔口宽度对液滴生成的影响，本文将孔口宽度wori分别设置为50、65、75、85、100 μm，不同孔口宽度通道内液滴破裂时刻的两相云图及液滴生成周期tcycle和直径Ddroplet分别如图6 和图7 所示。由图6 可知，随孔口宽度的收缩，液滴生成直径和周期逐渐减小，图7显示液滴生成直径和周期与孔口宽度呈近线性正相关。

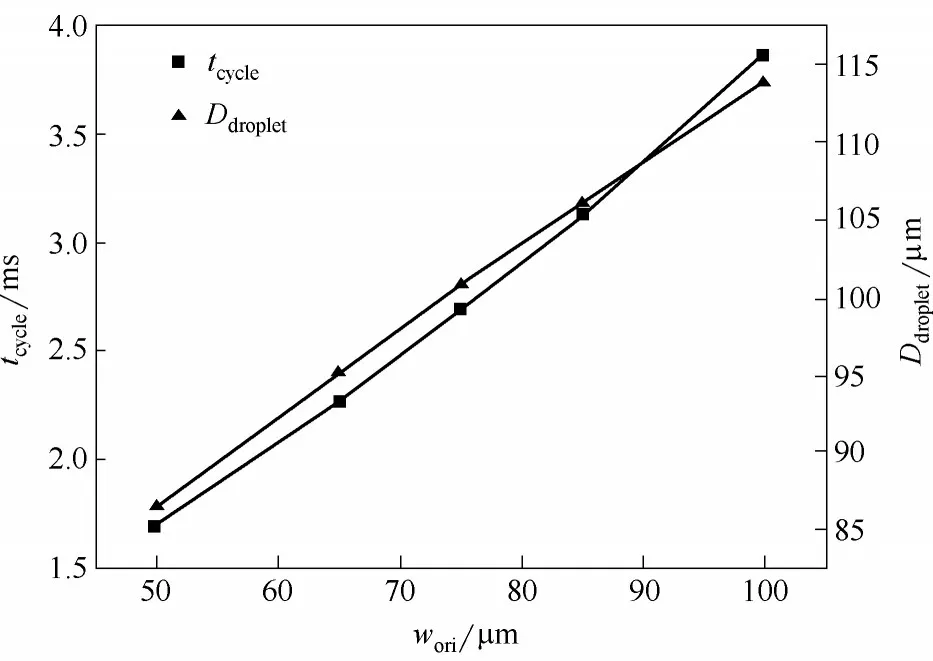
图7 液滴生成周期tcycle和直径Ddroplet随孔口宽度的变化Fig.7 Variation of droplet formation cycle and diameter with orifice widths

图8 各监测点速度随孔口宽度的变化Fig.8 Velocity component of each monitoring point varies with orifice widths

为揭示其内在的动力学成因，本文选取了位于两相流交汇区内的a、b 两点[如图8（a）所示，a 点坐标(150 μm，0 μm)，b点坐标(150μm，40 μm)]，并进行监视。随孔口宽度的逐渐减小，图9(a)中b点的Y方向速率|vb,y| 在整个周期内的平均值逐渐增大，图9(b)中a 点X 方向速率|va,x|在t3～t4时间段内以更大的加速度加速至最大值。可见，孔口的收缩阻碍了连续相下游方向的移动，也因此强化了连续相Y 方向的速度动量，即强化了对液滴竖直方向的挤压作用。

在对点a和b的监测中发现，各点单个周期的X或Y方向速度分量在不同通道内均呈现出类似的波动变化，如图9(a)、(b)所示。为阐明该波动性变化，本文在图9(a) 中对wori= 50、100 μm 两通道内的vb,y曲线转折点（ta1～ta5，te1～te5）进行了标示，显然vb,y在相邻两点的时间区间内均呈单调性变化，且各时刻点所对应的液滴生成轮廓及速度与压力场如图9(c)所示。结合图9(a)、(c)可知，在t1～t2区间内，界面张力占主导作用下的液滴回弹使得vb,y急剧减小；在随后的t2～t3区间内，液柱前沿的持续回弹进而减小了连续相向下游的流动阻碍，vb,y也开始逐渐增大。在t3～t4区间内，液滴的回弹及分散相持续流入的共同作用使得液柱体积逐渐膨胀，且其边界逐渐向b 点趋近，使得vb,y开始逐渐减小；此间，液柱前沿略微向下游延伸。从t4时刻开始，b 点正下方的液柱宽度在达到最大值后开始持续收缩，这主要由于液柱前沿持续向下游移动，使得连续相的流动空间逐渐被分散相所占据，也即等效于通道截面的收缩促使了vb,y的持续增大，其对液柱Y 方向的挤压作用（黏性正应力）也得以强化，从而促进了b 点正下方液柱宽度的持续收缩直至液滴破裂。总体而言，孔口的收缩减少了连续相的流通截面面积，连续相在孔口处的动量因此得以强化，这反过来促进了其对液柱在Y 方向的挤压和X 方向的黏性剪切拖拽作用。

为了更严格地阐明孔口影响液滴生成的作用机制，本文进而基于可比性原则，聚焦于不同通道内处于相同颈部宽度(Wneck=20 μm）的分散相液柱[图9(d)]，并对此时通道内b 点的Y 方向速度分量大小|vb,y| 进行了对比，如图8（b）所示。结果显示，孔口宽度逐渐增大，|vb,y|逐渐减小，也即连续相Y 方向对液滴的黏性正应力μ ∂vy∂y 逐渐减小，液滴在形成过程中受连续相的挤压作用逐渐减弱，从而导致液滴生长和挤压阶段所经历的时间随着孔口宽度增大而持续增加[如图10 所示，图10（a）中曲线对应于液滴生成的挤压阶段，曲线终点为液滴断裂时刻，也即液滴生成周期]。

图10（a）显示了不同孔口通道内液滴颈部宽度Wneck和位置Xneck随时间的变化。可见，随时间的推移，Wneck不断减小，Xneck呈先减小后增大的变化趋势，且在图10（a）中所示的t2～t3阶段发生转折。图10（b）中的相图显示，液滴颈部宽度均在孔口入口处开始形成，此后颈部不断被挤压，颈部下游液柱不断膨胀，颈部位置逐渐向上游移动。当颈部位置移动至转折点t2处，也即最小X 坐标位置，颈部位置在随后相当长的时间内（t2～t3）保持不变。

图9 单个生成周期内监测点速度、液柱轮廓、速度场和压力场随时间的变化Fig.9 Monitoring velocity,droplet profile and velocity and pressure field in a single cycle

然而，图10（a）显示，孔口宽度越大，液滴颈部可在固定的最小X坐标位置处持续被挤压的时间越长，也即时间段t2～t3越长。这主要由于孔口宽度越大，连续相向下游流通的阻碍越小，其对分散相的黏性拖曳和挤压作用相对较弱，颈部下游液柱在表面张力作用下显著膨胀，同时流经颈部的分散相流体速度也相对较小，二者的协同作用在一定程度上抑制了液滴颈部向下游移动的趋势。此外，颈部收缩率随孔口宽度的增大而不断减小，且在最小X 坐标位置区间内（t2～t3），颈部呈近线性收缩。随着颈部持续收缩，颈部内部分散相流速不断增大，同时颈部收缩阻碍了来流分散相的流动，导致颈部上游局部压力增大，当压力增大至某一临界值时，颈部位置开始向下游移动（t3～t4），也即在整个液滴挤压破裂过程中，颈部位置呈阶梯型变化。

3.2 竖直边锥形角对液滴生成的影响

在微流控液滴生成实验中，尽管很多研究通常从经验上将分散相入口经过拉丝处理形成锥形结构，但该结构对液滴生成的影响却少有研究。因此，这也是本文研究的主要动机。首先，保持锥形入口直径不变（或三角形竖直边长度不变Lver= 30 μm），将三角形斜边与竖直边的夹角θ1分别设置为20°、30°、40°、50°、60°和70°，其通道结构及液滴破裂时的相图如图11 所示。此外，液滴生成周期tcycle和直径Ddroplet与θ1的对应关系如图12所示。

图10 挤压阶段内颈部宽度和位置随时间的变化Fig.10 Variations of neck width and position in squeezing stage

当孔口宽度为50 μm，竖直锥形角θ1由20°增大至40°时，液滴生成周期和直径逐渐减小；而当θ1继续由40°增大至70°时，液滴生成周期和直径呈增大趋势。为解释其内在的动力学成因，本文对位于两相交汇区内的c 点进行监视[c 点坐标(120 μm，0 μm)，如图13（a）所示]。当液滴断裂时，不同通道内c 点X 方向速度大小|vc,x|的对比如图13（b）所示，锥形入口的局部速度场如图14所示。结果显示，锥形角连接处有回流形成，且当θ1由20°增大至40°时，回流区域及强度逐渐增大，从而削弱了分散相来流的动量，流入交汇区的分散相液柱也更易受到连续相的剪切作用，液滴生成周期因此持续减小。当θ1由40°增大至70°时，锥形角交汇处的回流区域及强度变化相对较小，但入口截面面积的减小更为显著，因此对分散相具有更强的聚焦作用，也即分散相在两相交汇处的X 方向速度逐渐增大，液滴生成周期随之持续增大。

图11 不同竖直边锥形角下液滴断裂时刻两相云图Fig.11 Two-phase cloud diagrams at droplet break-up under different θ1

图12 液滴生成周期tcycle和直径Ddroplet随竖直边锥形角的变化Fig.12 Variation of droplet formation period and diameter with θ1

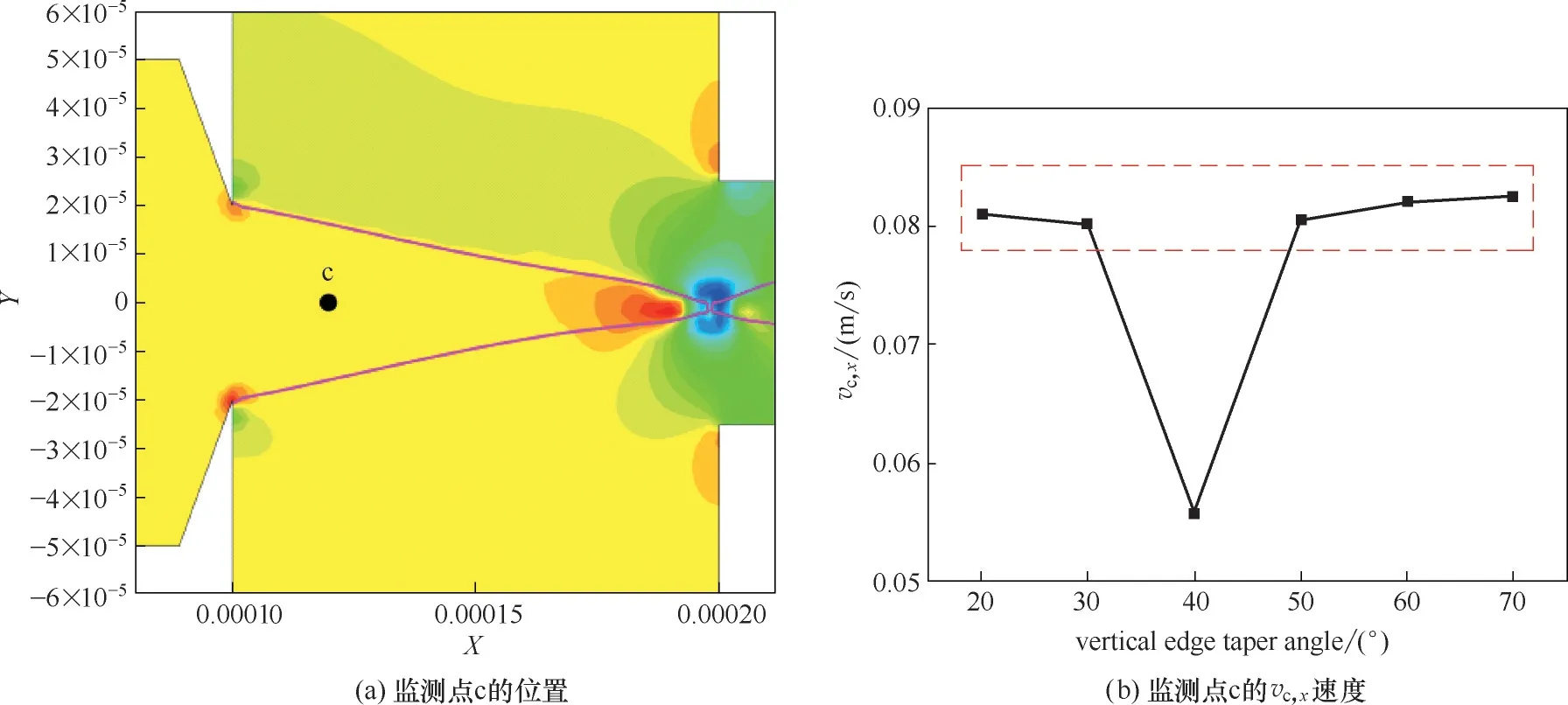
图13 两相交汇区内c点vc,x速度随竖直边锥形角的变化Fig.13 Variation of vc,x for different θ1

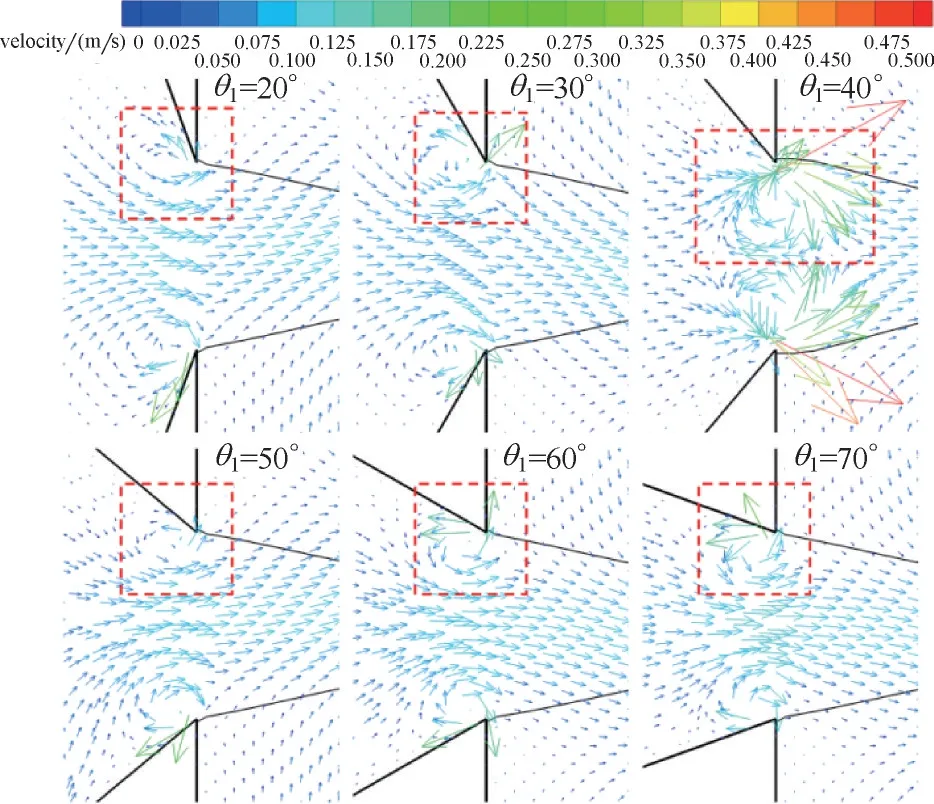
图14 液滴断裂时刻锥形入口的局部速度场分布图Fig.14 Local velocity field of taper inlet at droplet break-up

尽管液滴的生成周期和直径随θ1的增大呈先减小后增大趋势，但整体上，改变θ1对液滴生成周期（1.526～1.588 ms）和直径（83.5～84.7 μm）的影响并不大，这主要由于不同的锥形角通道均具有相同的锥形入口宽度。

3.3 水平边锥形角对液滴生成的影响

当锥形角水平边长度恒定Lhor= 50 μm，将水平边与斜边的夹角θ2分别设置为0°、10°、20°、30°和40°时，不同水平边锥形角结构下液滴破裂时的相图及液滴生成周期tcycle和直径Ddroplet分别如图15 和图16所示。整体上看，尽管θ2的变化会引起液滴生成周期的波动性变化，但对应液滴生成周期和直径的影响范围相对较小，1.562 ms≤tcycle≤1.716 ms，84.2 μm≤Ddroplet≤86.9 μm。然而，图15 显示不同锥形角θ2对应了交汇区内液柱轮廓的明显变化。因此，液滴生成对锥形角θ2不敏感的原因可能在于：相对于锥形角θ2，较小的孔口宽度（wori= 50 μm）对液滴生成特性的影响更为显著。

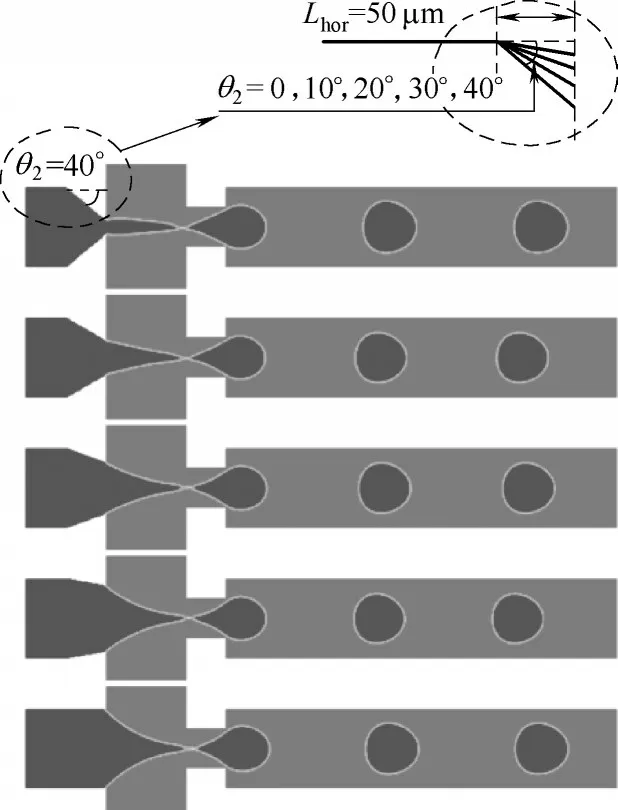
图15 不同水平边锥形角下液滴断裂时刻两相云图Fig.15 Two-phase cloud diagrams at droplet break-up under different θ2

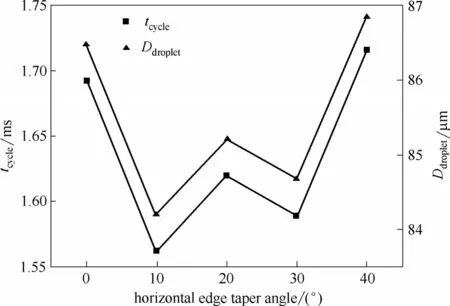
图16 液滴生成周期tcycle和直径Ddroplet随水平边锥形角的变化Fig.16 Droplet formation period and diameter for different θ2

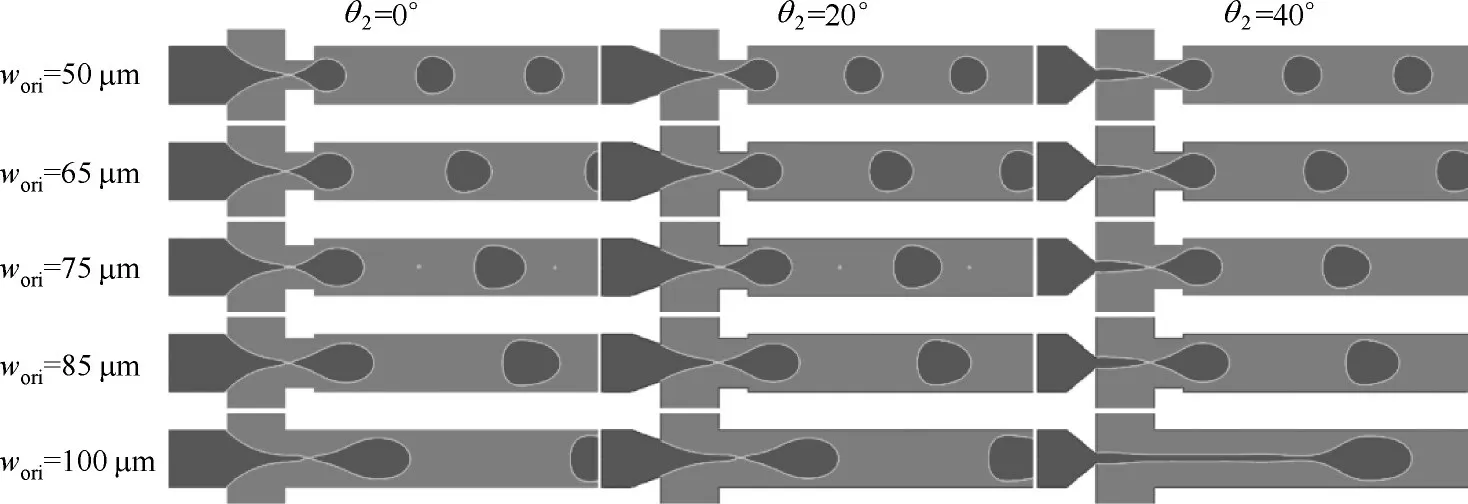
图17 不同水平边锥形角和孔口宽度下液滴断裂时刻两相云图Fig.17 Two-phase cloud diagram at droplet break-up under different θ2 and wori

为进一步探究wori和θ2对液滴生成的协同影响，本文进而模拟并对比了15 个不同通道构型内的液滴生成特性，其中θ2分别设置为0°、20°和40°，wori分别设置为50、65、75、85、100 μm，同时对位于两相交汇区内的a点进行监视。各通道构型内液滴破裂时的相图及液滴生成直径和周期分别如图17 和图18所示。显然，当wori= 50 μm 时，改变θ2的角度对液滴生成的影响相对不显著；然而，当wori=100 μm时，θ2的增大使得液滴生成模式由滴流向射流转变；这也表明：液滴的生成明显受到wori和θ2的共同影响，只是当wori较小时，孔口对液滴生成的影响更显著。

图18 液滴生成周期tcycle随水平边锥形角和孔口宽度的变化规律Fig.18 Variation of droplet formation period under different θ2 and wori

此外，图18 显示：当wori= 50 μm 时，θ2= 20° 所对应的液滴生成周期比θ2= 0° 和40°时相对较小，也即液滴生成周期与θ2并非呈单调的函数变化关系；而当wori=75、85 μm时，θ2=40°所对应的液滴生成周期最小且与θ2=20°极为相近。为探究其内在的动力学成因，本文对比了不同通道内流体流经a点的X 方向速度(va,x)随时间的变化，如图19所示，发现随着孔口宽度的增大，相同锥形角通道内液滴分散相的流速不断减小。其中，t1～t2为液滴的生长阶段，t2～t3为液滴的挤压破裂阶段。

图19 单个生成周期内监视点a处不同水平边锥形角下va,x速度随时间的变化Fig.19 Change of va,x in a single generation cycle at different θ2

由表1可知：当wori=50 μm 时，不同锥形角θ2对液滴挤压阶段所消耗时间的影响相差不大，且在整个生成周期内占比相对较小，分别为26.757%、26.280%和24.753%，表明在液滴生成过程中，较小的孔口对分散相产生了较强的聚焦效应，因此液滴能在相对较短的时间内挤压破裂。此外，wori= 50 μm时，锥形角θ2的变化对液滴生成周期影响较为微弱，表明孔口宽度对液滴形成起主要影响。当wori=75 μm 时，不同锥形角θ2对液滴挤压阶段所消耗时间在整个生成周期内占比分别为32.427%、31.679%和16.041%，可见锥形角θ2=0°，20°对液滴挤压阶段所消耗时间的影响相差较小，但与wori=50 μm 时相比，其在整个液滴生成周期内占比增大，表明孔口的聚焦作用相对减弱；而θ2= 40°时，液滴挤压阶段所消耗时间显著缩短，表明在该通道构型情况下，较大的锥形角开始显著影响液滴的生成特性。当wori=100 μm时，θ2=0°，20°时，通道内液滴呈滴流模式；当θ2增大至40°时，由于锥形角对分散相产生相对较强的聚焦作用，使得通道内分散相流动呈射流模式。在滴流模式下，θ2=0°，20°时，液滴挤压破裂阶段耗时占比进一步增大，分别为45.148%、47.532%，这表明当wori= 100 μm 时，孔口对连续相的聚焦作用进一步减弱。由此可见：较小的孔口可对连续相产生较强的聚焦作用，从而强化其流动剪切作用，此时锥形角的变化对液滴生成的影响相对较弱；当孔口宽度较大时，连续相的聚焦也持续减弱，此时锥形角对分散相的聚焦作用可显著影响液滴的生成特性。

表1 不同通道构型下液滴生长与挤压破裂阶段所经历时间的对比Table 1 Comparison of droplet growth and squeez fracture under different channel configurations

4 结 论

在微流控技术中，微通道结构的优化设计是一种被动实现液滴精确调控的有效方法。本文采用VOF/ CSF 耦合level set 的方法数值模拟了聚焦流通道局部几何构型，包括分散相入口、通道下游孔口以及二者共存模式下的通道结构变化对液滴生成特性的影响，具体结论如下。

(1)在十字聚焦型微通道内，下游孔口宽度的收缩，使得连续相的流通截面面积相应减小，连续相在孔口处的动量因此弱化，即削弱了连续相对分散相液柱在Y 方向的挤压和X 方向的黏性剪切拖拽作用，导致液滴生成周期和直径随着孔口宽度wori呈近线性变化。此外，颈部宽度的收缩速率随孔口宽度wori的增大而不断减小，孔口宽度越大，液滴颈部在颈部位置转折点处的挤压时间越长，且在转折点处的挤压过程中，颈部宽度呈近线性收缩。

(2) 当wori= 50 μm 时，竖直边锥形角θ1由20°增大至40°时，液滴生成周期和直径逐渐减小；而当θ1继续由40°增大至70°时，液滴生成周期和直径呈增大趋势。但整体上，液滴生成周期和直径对竖直边锥形角θ1的变化不敏感，这主要由于不同的锥形角θ1通道均具有相同的锥形入口宽度。因此，在该孔口宽度条件下，改变θ1难以实现液滴生成周期和尺寸的有效调控，但这可为以后通道结构的设计提供重要参考。

(3)当孔口宽度较小（wori=50 μm）时，液滴生成对锥形角θ2的变化同样不敏感，这主要由于孔口较强的聚焦效应主要影响液滴生成。而当孔口宽度较大（wori=100 μm）时，改变水平边锥形角θ2，液滴生成周期和直径随θ2的增大而增大，液滴流型可由滴流向射流模式转变，表明水平边锥形角对分散相的聚焦作用对液滴生成开始发挥主要作用。

(4)微通道内液滴的生成受分散相入口锥形角和孔口宽度的协同影响，且当孔口较大时，入口锥形角可作为对液滴尺寸进行微调的一种有效手段。此外，当其他条件不变，且通道内分散相流型为射流时，缩小通道的孔口宽度即可对射流模式加以抑制。而当通道内分散相流型为滴流时，为获取更大的液滴尺寸，宜选择孔口宽度和分散相入口锥形角较大的微通道。

符 号 说 明

Ddroplet——液滴直径，μm

Lhor,Lver——分别为锥形角水平边、竖直边长度，μm

Lo——出口段主通道长度，μm

Lori——孔口长度，μm

Qc,Qd——分别为连续相、分散相流量，μl/h

t——时间，ms

tcycle——液滴生成周期，ms

va,x,vc,x——分别为监测点a、c在X方向速度，m/s

vb,y——监测点b在Y方向速度，m/s

vc,vd——分别为连续相、分散相速度，m/s

Wneck——颈部宽度，μm

wc,wd——分别为连续相、分散相入口段通道宽度，μm

wo——出口段主通道宽度，μm

wori——孔口宽度，μm

Xneck——颈部位置，μm

θ——两相入口夹角，(°)

θ1——三角形斜边与竖直边夹角，(°)

θ2——三角形斜边与水平边夹角，(°)

μc,μd——分别为连续相、分散相黏度，mPa·s

ρc,ρd——分别为连续相、分散相密度，kg/m3

σ——表面张力系数，mN/m