基于粗糙颗粒动理学流化床内颗粒与幂律流体两相流动特性的数值模拟研究

田瑞超，王淑彦，邵宝力，李好婷，王玉琳

（东北石油大学石油工程学院，黑龙江大庆163318）

引 言

液固流化床具有颗粒与液体混合较为均匀，传质传热速率高等优点[1-3]，广泛应用于生物工程、环境工程、食品加工、离子交换、吸收等领域[4-8]。但液固系统本身具有非线性、结构不均匀性和流域多态性[9-11]，使得流化床内液固两相流动特性较为复杂。颗粒动理学理论是针对高浓度颗粒流动研究的理论与方法，其借鉴气体分子动力学理论，改进了对颗粒碰撞的描述。颗粒动理学假设颗粒做平动运动，颗粒间的碰撞为二体非弹性碰撞，颗粒间的碰撞概率由颗粒径向分布函数来确定。目前已广泛应用该理论对流固两相流动特性进行研究[12-14]。然而该理论假设颗粒为光滑颗粒，忽略颗粒做旋转运动。实际上，颗粒表面往往具有粗糙度，对于表面粗糙的颗粒，颗粒在相互作用过程中不仅产生瞬时直接碰撞作用，同时会产生摩擦作用。颗粒相互摩擦作用传递剪切应力、相互挤压传递正压力，这就使得颗粒在彼此间相互碰撞以及液相湍流等作用下产生旋转[15]。颗粒旋转现象普遍存在于多相流动中，如固体颗粒在管道内气力、液力输送，各种气固、液固分离装置等。颗粒旋转不但会影响颗粒的运动轨迹，而且对固相流场以及周围的气相或液相流场也会产生相应的影响[16-19]。这意味着颗粒旋转在流固两相流动中的作用是不容忽视的。

含有颗粒的幂律流体流动广泛存在于石油化工、食品生产以及日常生活中。这种流固体系往往具有非线性和多态性，其流动机理较为复杂[20]。相当多研究人员的研究重点主要集中在幂律流体的流动特性。Patel等[21]运用考虑润湿性引起能量损失的力学模型分析了剪切稀释流体填充床内的压降特性和剪切应力。de Castro 等[22]通过实验系统地研究了剪切稀化流体流经颗粒时，流体剪切流变特性对非达西流的流量与压降关系的影响。Qi等[23]采用格子Boltzmann 模型研究了不同Reynolds 数和幂律指数下填充床内的幂律流体流动，而很少有研究是针对颗粒与幂律流体两相流动。因此本文在应用Goldshtein 等[24]提出的考虑颗粒旋转的稠密、近理想弹性、微粗糙颗粒动理学理论的基础上通过改变液相黏度方程和Reynolds数方程对流化床内含有颗粒的幂律流体流动特性做了进一步的研究。

1 含有颗粒的幂律流体两相流动的粗糙颗粒动理学

1.1 粗糙颗粒的控制方程

为了便于分析，本文假设颗粒为球形，且颗粒的尺寸和物理性质相同；颗粒为准刚性颗粒，颗粒的形状在碰撞前后不会发生改变；仅考虑两颗粒间的碰撞；碰撞为点接触，碰撞产生瞬时冲力，不考虑碰撞瞬时其他外力的作用。

高浓度下，颗粒间碰撞产生的冲量使得颗粒动量发生了变化，同时颗粒之间的摩擦作用又会使得颗粒能量发生转移，从而导致颗粒旋转速度的产生或者发生改变，进而颗粒的运动状态发生改变。粗糙颗粒动理学除了采用传统的弹性恢复系数e 来表示颗粒碰撞引起的能量耗散外，还引入了切向弹性恢复系数β 来表征粗糙颗粒的摩擦和弹性变形。β取值范围为-1～1，β=-1 时表示颗粒表面光滑，颗粒碰撞前后在切向方向上的相对速度没有发生改变；β=1 时则表示为颗粒表面完全粗糙，颗粒碰撞前后在切向方向上的相对速度大小不变而方向相反。

由颗粒动理学可知[25]，颗粒相平动拟温度θt为

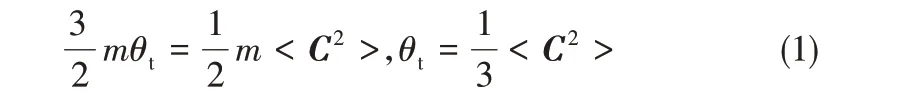
式中，C=c-u，为颗粒平动脉动速度，m/s。

当颗粒具有旋转速度时，颗粒相旋转拟温度θr表示为

式中，W=w-w0，为颗粒脉动角速度（w 为颗粒瞬时角速度，w0为颗粒平均角速度）；m 为单个颗粒质量，kg；Is为转动惯量，kg·m²。

在实际液固两相流动中，颗粒速度脉动能量含有平动速度脉动能量和旋转速度脉动能量，因此，颗粒总脉动能量E为

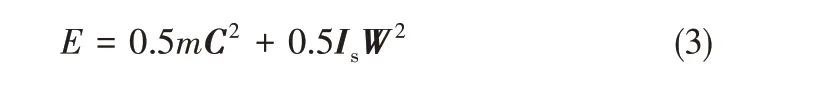
类比于颗粒平动拟温度与旋转拟温度的定义，引入了颗粒拟总温e0的概念[24]

基于颗粒动理学的理论框架，推导出了颗粒相的流动守恒方程。对于颗粒相的处理采用的是稠密气体分子动理学理论的经典结果[26]，根据Maxwell输运理论可以得到颗粒相的质量以及动量守恒方程[25]

式中，εs为颗粒浓度；ρs为颗粒密度，kg/m3；us=＜c＞为颗粒平动速度矢量，m/s；ps为颗粒相压力，Pa；τs为颗粒相应力张量，Pa；g 为重力加速度矢量，m/s2；p 为液相压力，Pa；βls为液固相间的曳力系数，kg/(m3·s)。

颗粒拟总温守恒方程为

式中，χs为由颗粒碰撞造成的脉动能量耗散，kg/(m·s3)；Dls为液固相间交换的脉动能量，kg/(m·s3)；（-psδ+τs）为颗粒相总应力P。

根据Chapman-Enskog 单颗粒速度分布函数可以表示如下[24,26]

颗粒速度分布函数f(1)依赖于颗粒速度分布函数f(0)，是颗粒质量、动量和能量组合的函数[26]。

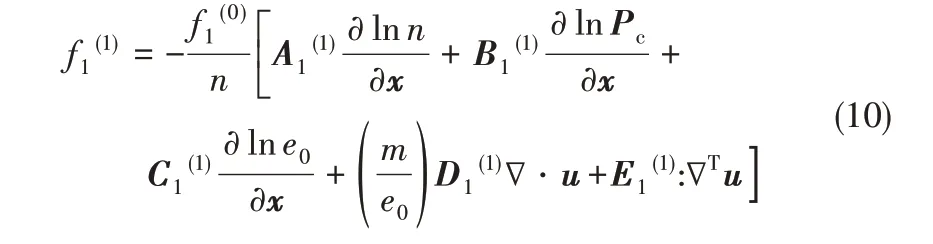
式中，A(1)、B(1)、C(1)、D(1)、E(1)分别为无量纲平动速度C[m/(αte0)]1/2和转动速度W[Is/(αre0)]1/2的函数。矢量系数A(1)，B(1)，C(1)为颗粒碰撞对动能传递的作用。张量系数E(1)表征颗粒黏性系数，系数D(1)反映颗粒体积黏性系数。

根据式（8）可将颗粒相总应力写成线性表达的形式[24,26]

式(11)右侧第一项遵循各向同性原理，表示的是f(0)对零阶颗粒相应力P(0)的贡献。考虑颗粒旋转，颗粒相总应力P会发生变化，包括颗粒运动对颗粒速度分布函数产生贡献Pk和颗粒碰撞对颗粒速度分布函数产生贡献Pc。平动和转动作用下的颗粒相动力分量Pk和碰撞分量Pc分别为[24,26-27]

由式（9）和式（12），在六维速度空间积分时颗粒转动脉动速度对颗粒压力无影响，仅与颗粒平动脉动速度有关，积分得P(0)(f(0))[24,26]

P(1)(f(0))是由颗粒碰撞产生的非局部效应引起。由式（9）和式（13）积分可得[24,27]

P(1)(f(1))表征由颗粒碰撞产生的局部效应引起一级速度分布f(1)对颗粒相应力的影响。由式（10）和式（13）积分得[24,27]

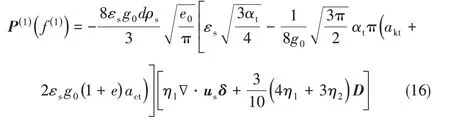
根据式（14）～式（16）可将式（11）写成如下形式

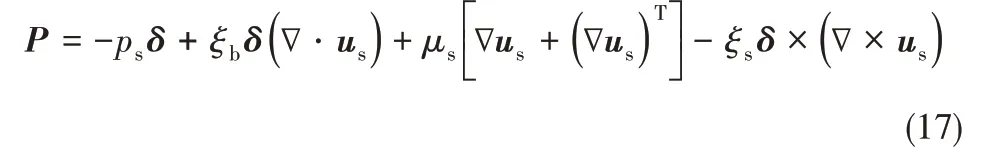
式（17）右边第一项为颗粒相压力，由式（14）和式（15）求得。由式（15）和式（16）可求得颗粒相剪切应力方程为

针对所研究的幂律流体，采用了Kemblowski等[30]提出的修正的Reynolds数定义

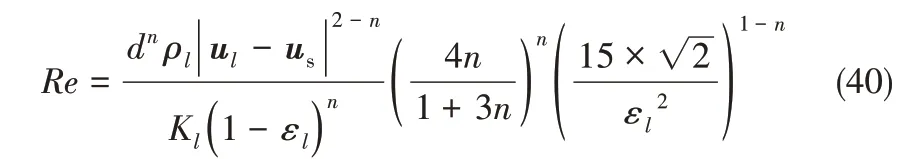
1.3 边界条件

在壁面处，对Jenkins 等[31]提出的边界条件进行修正，得到的“小摩擦/全滑移”极限为

式中，S为剪切应力，Pa；N为颗粒碰撞产生的法向应力，Pa；Q为由壁面提供给颗粒相的脉动能量通量，其可被视为一种能量来源；μ 为颗粒与壁面之间的摩擦系数，此次模拟采用的摩擦系数为0.2。初始时刻，流化床内填充一定数量的球形颗粒，床内液体和颗粒保持静止。流化床底部为液体入口，液体速度依照实验条件设置，液体的温度为25℃，由于模拟采用的为不可压缩流体，因而模拟时将密度设置为常数，流化床顶部设置为压力出口。颗粒弹性恢复系数e 取为0.95，颗粒切向弹性恢复系数β 取为-0.2，壁面弹性恢复系数ew取为0.9。所有模拟均采用Gidaspow 曳力模型。控制方程的离散采用Superbee差分格式。

2 计算结果与讨论

2.1 Broniarz-Press等实验

Broniarz-Press等[32]通过实验测量了不同液体速度下，含有颗粒的剪切稀释流体流化床床层的动态流化高度。实验[32-33]及模拟工况如表1 所示。流化床的底部为速度入口，顶部为压力出口，出口压力为大气压，模拟采用的网格尺寸为15×300。初始时刻，流化床内填充颗粒的浓度为0.578。液体为幂律流体，其黏度符合幂律流变模型，流动指数n 为0.82，稠度系数Kl为0.013 Pa·sn。所有算例运行时间为30 s，取20～30 s 作为时间平均样本。采用1×10-6～1×10-3s的自适应计算步长。

图1为不同表观液速下计算得到的床层动态高度与实验值的比较。从图中可以看出采用KTRS 模型与KTGF 模型得到的模拟结果均能很好地与实验值相吻合。两种模型的主要区别在于KTRS 模型考虑了由颗粒表面粗糙而产生的颗粒旋转作用，当液体流速较低时，颗粒的运动缓慢，颗粒旋转作用并不明显，从而使得两种模型所得到的模拟结果之间的差距相对较小。

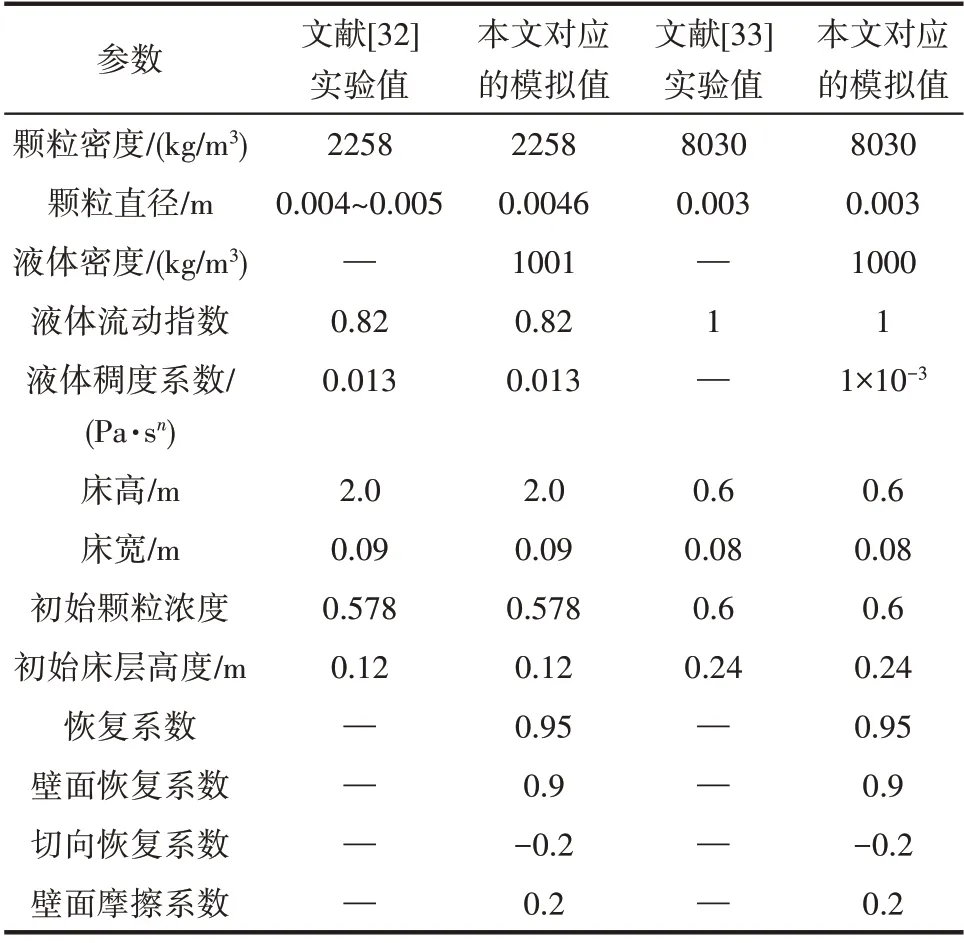
表1 文献［32-33］实验及本文模拟参数Table 1 Parameters used in simulations and experiments by Broniarz-Press et al.［32］and Ehsani et al.［33］

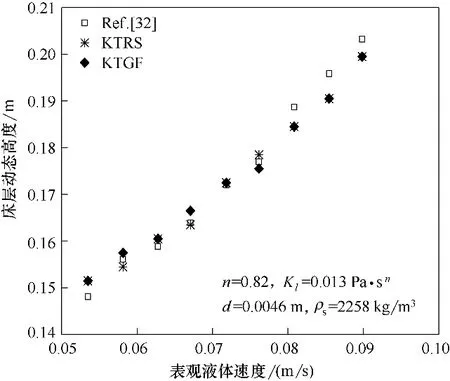
图1 床层动态高度随液体速度的分布Fig.1 Distributions of bed dynamic height as a function of superficial liquid velocity

图2 床层内瞬时液体黏度分布Fig.2 Instantaneous liquid viscosity in bed with KTGF and KTRS models

图2 为分别采用KTRS 模型与KTGF 模型得到的液体黏度的瞬时分布。计算得到的两种模型下的液体黏度具有相同的趋势。即初始时刻，床层中的液体黏度急剧下降，大约3 s 后，则在一定数值附近上下波动。将两种模型下的液体黏度进一步对比，可以看出KTRS 模型得到的液体黏度略大。这是由于此时液体的流动指数n＜1，液体表现出剪切稀释的特点，即剪切速率越大，液体黏度越小。由于KTRS 模型考虑了颗粒的旋转，增大了颗粒相间的动量以及能量的传递和耗散，颗粒在流化床内不易被液体所携带，液体的剪切速率减小，致使液体的黏度增大。

2.2 Ehsani等实验

为了进一步验证所提出模型的适用范围，对Ehsani等[33]所做的实验进行了数值模拟计算，Ehsani等通过记录床层顶部和底部的压力测量得到了液固流化床内的瞬时床层内液体体积分数。实验采用的液体为水，其密度和黏度均为常数，液体的密度为1000 kg/m3，黏度为1×10-3Pa·s。流化床的底部为速度入口，入口液体流速为0.219 m/s，顶部为压力出口，出口压力为大气压，采用20×150 的网格尺寸。初始时刻颗粒填充浓度为0.6。模拟采取自适应时间步长，计算时间为40 s，取30～40 s 的计算结果作为时均值。模拟采用的具体参数和条件如表1所示。

图3为采用两种模型模拟得到的床层内液体体积分数与Ehsani 等实验测量值的比较。从图中可以看出，采用KTRS 模型得到的床层内液体体积分数要小于采用KTGF 模型得到的床层内液体体积分数，且KTRS 模型计算得到的床层内液体体积分数与实验值更为接近，经计算在稳定状态下，采用KTRS 模型得到的时均床层内液体体积分数为0.659，而采用KTGF 模型得到的时均床层内液体体积分数为0.688，实验测量值为0.660。模拟结果进一步验证了KTRS 模型考虑了颗粒的旋转作用，旋转造成了较大的能量耗散，因而颗粒的运动能力减弱。

图3 瞬时床层内液体体积分数分布Fig.3 Instantaneous liquid volume fraction as a function of time in bed with KTGF and KTRS models

从以上的模拟结果与实测值的比较可以看出，所提出的模型既能够较好地预测流化床内牛顿流体-颗粒两相流动，又能够很好地预测流化床内幂律流体-颗粒两相流动。

2.3 流动指数的影响

流动指数是影响幂律流体黏度的一个重要参数，当0＜n＜1 时，随着剪切速率的增加，流体黏度降低，幂律模型表现出流体剪切稀释的特点。而当n＞1 时，随着剪切速率的增大，流体黏度增大，此时幂律模型则表现出流体剪切稠化的特点。本文在模拟Ehsani 等[33]实验的基础上，通过改变液相的流变特性，将稠度系数Kl设置为0.001 Pa·sn，分别采用粗糙颗粒动理学模型和颗粒动理学模型计算了流动指数在0.7～1.5时，流变特性由剪切稀释转变到剪切稠化时，流化床内的液固两相流动特性。

图4 为采用KTRS 模型时流化床内瞬时颗粒浓度分布图及速度矢量图。从图中可以看出流化床内呈现出明显的颗粒聚团与涡旋并存的非均匀性结构，颗粒聚团主要发生在流化床的近壁区域。这是由于考虑颗粒旋转作用后，增大了颗粒相间动量和能量的传递和耗散，颗粒趋于团聚。随着流动指数的增加，液体对颗粒相的作用增强，因而颗粒分布更为均匀。

为了能够进一步地研究不同流动指数下流化床内的颗粒聚团的变化，采用Subbarao[34]提出的颗粒聚团计算方程对不同流变指数下的流化床内的颗粒聚团尺寸进行了计算，其方程为

图4 不同流动指数下流化床内瞬时颗粒浓度分布图及速度矢量图Fig.4 Distributions of particle concentration and velocity in fluidized bed at different flow indexes

式中，（1-εl）为平均颗粒浓度；εc为颗粒聚团内的液体体积分数；ut为单颗粒的终端速度；D 为流化床直径；d 为颗粒直径。εc采用Harris 等[35]提出的公式计算

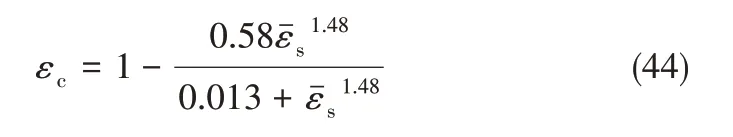
式中，εˉs为一定高度处的截面平均颗粒浓度。

图5 为采用KTGF 和KTRS 模型时得到的流化床内的颗粒聚团尺寸随流化床高度的分布。从图中可以看出：两种模型都能够预测流化床内颗粒聚团的出现，且在流化床的中下部，采用KTRS 模型计算得到的颗粒聚团尺寸要明显高于KTGF 模型。采用KTRS 模型时，不同流动指数下的聚团尺寸之间的差距要明显大于KTGF 模型，这表明液体流动指数的改变对于颗粒的旋转运动有较大的影响。

本文采用了加权平均的方法计算得到了颗粒拟温度的平均值。

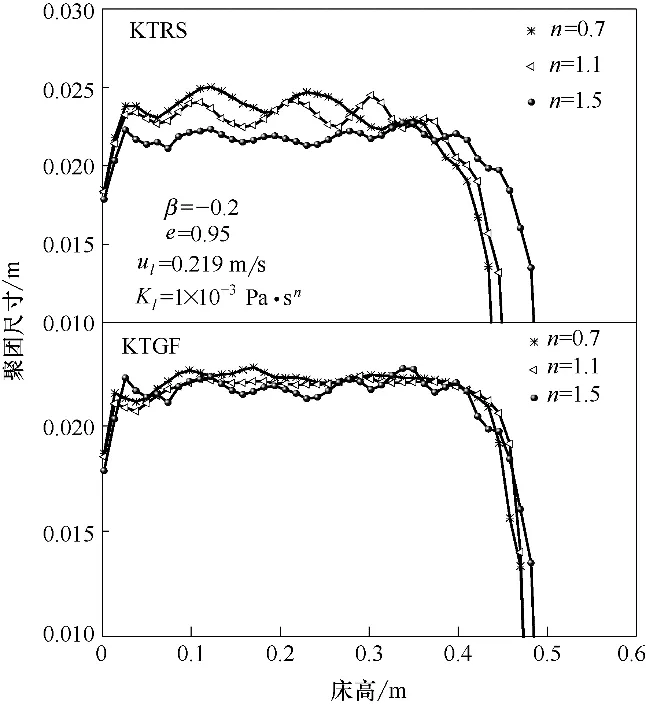
图5 不同流动指数下颗粒聚团尺寸随床高的变化Fig.5 Profile of cluster size along bed height at different flow indexes

图6为床层内时均颗粒拟温度随流动指数的变化。从图中可以看出无论是采用KTRS 模型还是采用KTGF 模型，颗粒拟温度随颗粒浓度的增加均呈现出先增大达到最大值后再减小的趋势。经计算在流动指数为0.7、1.1 和1.5 时采用KTRS 模型得到的颗粒拟温度分别为6.51、6.79 和7.56 cm2/s2，而采用KTGF 模型时得到的颗粒拟温度分别为10.58、10.84 和9.33 cm2/s2。可以看出相比于KTGF 模型，采用KTRS 模型得到颗粒拟温度要更小，这表明颗粒间由旋转造成的能量传递和损耗增大，从而削弱了颗粒速度的脉动。

图6 不同流动指数下时均颗粒拟温度随颗粒浓度的变化Fig.6 Time-averaged granular temperature as a function of particle concentration at different flow indexes

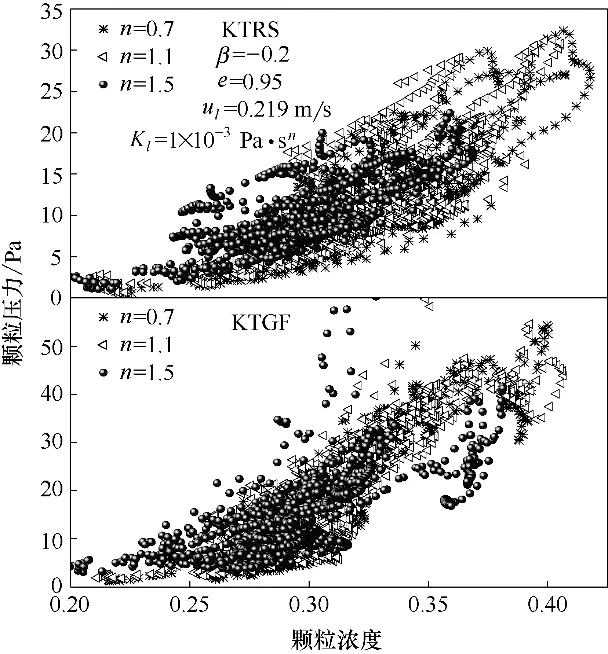
图7 不同流动指数下颗粒压力随颗粒浓度的变化Fig.7 Time-averaged solids pressure as a function of particle concentration at different flow indexes

图7表示床层内时均颗粒压力随颗粒浓度的变化。可以看出随着颗粒浓度的增加，颗粒压力增大。由式（14）可知，颗粒压力由两部分组成：颗粒动力分量和碰撞分量。经计算在流动指数为0.7、1.1 和1.5 时采用KTRS 模型时得到的颗粒相平均压力分别为11.79、11.64 和9.51 Pa，而采用KTGF 模型时得到的颗粒相平均压力分别为20.62、20.58 和14.53 Pa，这表明随着流动指数的增大，颗粒相压力逐渐减小。这是由于当颗粒浓度较高时，颗粒动力分量可以忽略，碰撞分量占主导地位，由于碰撞部分正比于颗粒浓度的平方，而床层颗粒浓度随流动指数的增大而减小，因此颗粒压力减小。将两种模型得到的颗粒相压力进行比较可以发现相较于采用KTRS模型得到的颗粒压力，采用KTGF模型得到的颗粒压力更大。这说明尽管考虑旋转作用的KTRS 模型得到的床层内的颗粒浓度较高，但采用该模型时得到的颗粒拟温度要远小于KTGF 模型。造成这一现象的原因是颗粒旋转削弱了颗粒的运动，即颗粒要提供一部分能量供自身做旋转运动。

图8 不同流动指数下液相湍动能耗散率随颗粒浓度的变化Fig.8 Distributions of turbulence dissipation as a function of particle concentration at different flow indexes

湍流耗散率表示的是流体的动能耗散速度，其在特定位置处的大小反映了该位置处的能量损失。图8 为时均液相湍动能耗散率随颗粒浓度的变化。经计算在流动指数为0.7、1.1 和1.5 时采用KTRS 模型得到的湍动能耗散率分别为0.168、0.186 和0.198 m2/s3，而采用KTGF 模型得到的湍动能耗散率分别为0.171、0.189 和0.243 m2/s3。由此可以看出，随着流动指数的增大，液相湍动能耗散率逐渐增大。这是由于随着流动指数的增大，液体对颗粒的携带作用增强，相间作用力明显，导致液体自身所消耗的能量增多。

2.4 稠度系数的影响

稠度系数是影响幂律流体黏度的另一个重要参数，由幂律流变模型的本构方程可知，随着流体稠度系数的增加，其黏度增大。为了研究稠度系数对流化床内液固两相流动特性的影响，本文在模拟Ehsani 等[33]实验的基础上，通过改变液相的流变特性，将流动指数设置为0.7，对稠度系数从0.001～0.007 Pa·sn范围内的同一流化床进行了模拟研究。

图9 为采用KTRS 模型模拟得到的流化床内瞬时颗粒浓度分布图及速度矢量图。从图中可以看出流化床内存在分散颗粒与颗粒团聚物并存的非均匀结构。随着稠度系数的增大，大的颗粒团聚物破碎成小的团聚物。这主要是因为液体黏度随着稠度系数的增大而增大，使得液固相间作用增强，而颗粒间的作用减弱，从而降低了流态化的不均匀性，提高了流态化的质量。

图9 不同稠度系数下流化床内瞬时颗粒浓度分布图及速度矢量图Fig.9 Distributions of particle concentration and particle velocity in fluidized bed at different consistency coefficients

图10 为采用KTGF 和KTRS 模型时得到的流化床内的颗粒聚团尺寸随流化床高度的分布。可以看出在流化床的中下部，采用KTRS 模型计算得到的颗粒聚团尺寸要明显高于KTGF 模型，且采用KTGF 模型时床层的膨胀高度要高于KTRS 模型。这是由于颗粒间的旋转摩擦会消耗更多的能量，从而使聚团尺寸增大。另外随着稠度系数的增大，颗粒聚团尺寸逐渐减小。

图10 不同稠度系数下颗粒聚团尺寸随床高的变化Fig.10 Profile of cluster size along bed height at different consistency coefficients

图11 为床层内时均颗粒拟温度随稠度系数的变化。经计算在稠度系数为0.001、0.004 和0.007 Pa·sn时采用KTRS 模型得到的颗粒拟温度分别为6.51、6.85 和7.06 cm2/s2，而采用KTGF 模型时得到的颗粒拟温度分别为10.58、11.41 和10.82 cm2/s2。由此可以看出随着稠度系数的增大颗粒拟温度也随之增大，采用KTRS 模型得到的颗粒拟温度要比采用KTGF 模型的小。这表明液体黏度的增加增大了对颗粒的曳力作用，从而提高了颗粒的运动能力，另外颗粒旋转摩擦消耗了更多的能量，致使颗粒的运动动力减弱。

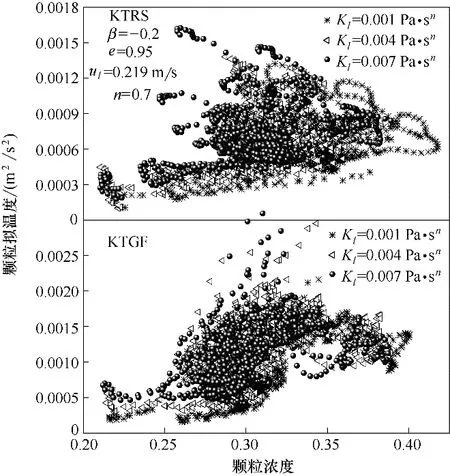
图11 不同稠度系数下时均颗粒拟温度随颗粒浓度的变化Fig.11 Time-averaged granular temperature as a function of particle concentration at different consistency coefficients

图12 不同稠度系数下时均颗粒压力随颗粒浓度的变化Fig.12 Time-averaged solid pressure as a function of particle concentration at different consistency coefficients

图12 表示床层内时均颗粒压力随颗粒浓度的变化。随着颗粒浓度的增加，颗粒压力增大。经计算当稠度系数为0.001、0.004 和0.007 Pa·sn时，采用KTRS 模型得到的颗粒相压力分别为11.79、10.85和10.40 Pa，而采用KTGF 模型得到的颗粒相压力分别为20.62、20.37 和18.60 Pa，由此可以发现随着稠度系数的增大，颗粒相压力逐渐减小。将两种模型得到的颗粒相压力进行比较可以发现相较于KTRS 模型，采用KTGF 模型时得到的颗粒压力更大。这是由于KTRS 模型考虑了颗粒的旋转作用，颗粒的旋转作用消耗了颗粒自身更多的能量。

图13 不同稠度系数下时均液相湍动能耗散率随颗粒浓度的变化Fig.13 Time-averaged turbulence dissipation as a function of particle concentration at different consistency coefficients

图13 为时均液相湍动能耗散率随颗粒浓度的变化。经计算当稠度系数为0.001、0.004 和0.007 Pa·sn时，采用KTRS 模型得到的湍动能耗散率分别为0.168、0.176 和0.203 m2/s3，而采用KTGF 模型得到的湍动能耗散率分别为0.171、0.189 和0.225 m2/s3，即随着稠度系数的增大，液相湍动能耗散率增大，这表明在一定条件下稠度系数越大越有益于颗粒在流体中的扩散，使得颗粒分布更加均匀。

3 结 论

分别采用粗糙颗粒动理学与颗粒动理学，对流化床内幂律流体与颗粒两相流动进行了数值模拟研究，将考虑颗粒旋转和未考虑颗粒旋转模拟得到的结果进行比较，结果表明粗糙颗粒动理学模拟得到的结果能够较好地与文献实验数据相吻合。与颗粒动理学模型相比，采用粗糙颗粒动理学得到的颗粒相压力、颗粒拟温度、床层内液体体积分数和液相湍动能耗散率较小，而当液体为剪切稀释流体时液体黏度相对较高，这主要是由于颗粒旋转作用增强了颗粒间动量和能量的传递和耗散。

模拟研究了流化床内幂律流体的稠度系数与流动指数对流体和颗粒两相流动特性的影响。结果表明在一定的范围内，无论是采用KTGF 模型还是采用KTRS 模型，随着流动指数和稠度系数的增加，颗粒拟温度和液相湍动能耗散率均增大，颗粒相压力均减小，这表明流态化的质量有所提高。且通过将两种模型模拟得到的颗粒拟温度和颗粒相压力结果进行比较可以发现，随着流动指数和稠度系数的增加，两种模型之间的差距先增大后减小，这表明此时随着液体黏度的增大，颗粒相旋转作用先增大后减小。

符 号 说 明

E——颗粒总脉动能量，(kg·m2)/s2

g0——径向分布函数

Ks——无量纲转动惯量

Re——Reynolds数

αr,αt——无量纲系数

μs——颗粒相剪切黏度，kg/(m·s)

ξb——颗粒相体积黏度，kg/(m·s)

ξs——颗粒相旋转黏度，kg/(m·s)

下角标

l——液相

r——旋转

s——颗粒相

t——平动

w——壁面