一种基于聚类分析的二维激波模式识别算法
2020-09-10常思源白晓征刘君
常思源,白晓征,刘君
大连理工大学 航空航天学院,大连 116024
激波的探测与可视化是计算流体力学(CFD)领域中一个非常富有挑战的问题。在某些流场参数的等值线云图中,通常认为激波间断位于大量等值线聚集处,但对于存在接触间断、膨胀波和旋涡等复杂波系干扰的流场,该方法很容易对激波产生误判,因此有必要发展更加精准的激波探测(Shock Wave Detection)技术。
至今,很多学者[1-14]基于激波捕捉(Shock-Capturing)法计算出的流场提出了各种各样激波探测的方法。1985年,Buning和Steger[1]首次提出将沿激波法向(近似用压强梯度方向代替)马赫数等于1的等值面视为激波面;该方法随后被Darmofal[2]称为基于正则马赫数(Normal Mach Number)的激波探测法,并逐渐在流场可视化中被广泛应用;Liou等[3]在此基础上介绍了3种滤波技术,以剔除辨识出的伪激波;随后,Lovely和Haimes[4]又成功将其推广到非定常流动中用以探测运动激波。1993年,Pagendarm和Seitz[5]详细地介绍了一种基于流场密度方向导数(Directional Derivative)来辨识激波的方法,即将密度二阶方向导数为0的等值面视为激波阵面,并结合密度的一阶方向导数(密度梯度在当地速度矢量上的投影)来过滤噪点;其后,Ma等[6]的数值算例表明基于正则马赫数过滤噪点可能会获得更好的结果。1994年,Van Rosendale[7]提出了一种针对二维非结构网格的激波拟合算法,通过比较网格节点之间的密度梯度来移动网格使其边缘与激波线对齐;Ma等[6]认为该算法中局部加权密度梯度的策略可以用于识别出激波附近的网格节点,但可能需要结合其他流场特征来实现更准确的辨识。2011年,Kanamori和Suzuki[8]巧妙地将特征线理论(Theory of Characteristics)运用于二维激波探测中,并成功推广到非定常[8]和三维流场[9]计算中,相比前述方法,该算法虽然较为复杂,但不需要人为设置一些经验性的阈值参数进行滤波就可以获得更加良好的结果。2017年,Akhlaghi等[10]通过分析数值纹影图内某些流动参数的高斯分布(Gaussian Distribution),提供了一种新的激波辨识方法,对连续流和稀薄流都比较适用。近年来还有学者[11-12]尝试将深度学习(Deep Learning)融入大规模流场的激波识别中,取得了不错的结果。
国内针对激波探测的研究报道相对较少,马千里等[13]基于压强梯度计算正则马赫数,并利用激波物理特征,结合光线投射法提出了一种基于两级采样的多激波提取方法。2013年,Wu等[14]在其综述中总结了以往激波辨识方法,并指出了对运动激波和弱激波的精确识别是非常有挑战的研究方向。
整体来看,以上这些激波探测法具有一个共同的特征,即它们都是基于“当地标准(Local Criteria)”进行辨识的;也就是说,激波位置的识别仅通过分析局部一个网格节点/单元(最多考虑一层相邻网格)上的流动参数来实现。Paciorri和Bonfiglioli[15]认为这些探测技术的当地性质正是其局限性和缺陷的根源。一方面,这些方法往往将探测到的一系列散点[6]或小线段[8-9]视为激波线/面,但由于数值耗散和振荡,这些激波线/面处经常会出现噪声、伪激波分支或空隙[14]。另一方面,所有这些算法都不能判断出流场中是否存在激波干扰点,即不能清晰地给出流场中激波干扰的模式,如λ激波、异侧激波相交、激波-壁面反射等。
近年来,有一批学者[16-19]重新开启了激波装配(Shock-Fitting)法的研究与应用,相比当前主流的激波捕捉法,该方法必须显式地处理激波,因此在开始计算前,通常都需要从激波捕捉流场获取相关信息,如合理的初始流动参数、激波的近似位置、激波的干扰结构等。然而,由于上述激波探测法的缺陷,其很难直接用于激波装配的初始化中[15],最终造成这些激波装配算法难免需要依据先验知识进行人工干预来设置初始激波及激波干扰点的位置。
针对上述问题,Paciorri和Bonfiglioli[15]于2012年介绍了一种二维激波模式识别技术,首先根据传统基于当地密度二阶方向导数的方法[6]提取出激波点云,随后利用霍夫变换(Hough Transform)搜寻这些散点中的特征直线并去除噪点,再采用最小二乘(Least-Squares)法拟合得到各条激波曲线,最后通过一套模糊逻辑(Fuzzy Logic)算法识别出激波干扰的模式。然而,该方法实施起来比较繁琐,对于流场中长度较短的激波分支容易产生误判,且很难适用于非定常流场。
本文提出了一种面向全局(Global)的二维激波模式识别算法,对探测出的激波带网格单元进一步处理,通过聚类分析(Cluster Analysis)方法将激波单元划分成许多簇;分析各个簇的相邻关系就可以清晰地判断出激波干扰的模式,最终基于Bézier曲线拟合算法优化的激波线和数值捕捉的激波相比在形状和位置上都较为吻合。该算法不仅逻辑简单,且不受网格类型的限制,同时在非定常流动中也具有较高的可靠性。
1 二维激波模式识别算法
结合一个定常无黏激波反射算例(几何模型和流场如图1所示,其中p表示压强,下标∞表示来流状态),从3个主要方面介绍了该二维激波模式识别算法的步骤和特点。在该算例中,来流马赫数Ma∞=1.5,楔角θ为10°,入口和出口高度分别为2.17L和2L。入射斜激波S1在上壁面发生马赫反射产生了强度较强的马赫干扰S2,而反射激波S3经膨胀波异侧干扰后强度下降,最后在下壁面产生了正规反射,次反射激波S4与出口边界相交。此外,虽然该流场是基于均匀的非结构三角形网格(网格尺寸Δ=0.015L)计算的,但是该识别算法同样适用于结构网格、混合网格和非均匀网格等,在2.2节有相关描述。
1.1 辨识激波单元
本文算法是针对网格单元而非网格散点实现的,因此首先需要从图1所示流场提取出表征激波位置的网格单元,即图2所示激波单元。考虑到引言所述若干激波探测方法的适用性和鲁棒性,本文基于流场单元格心的压强梯度,设计了一套针对激波的辨识准则,具体步骤为
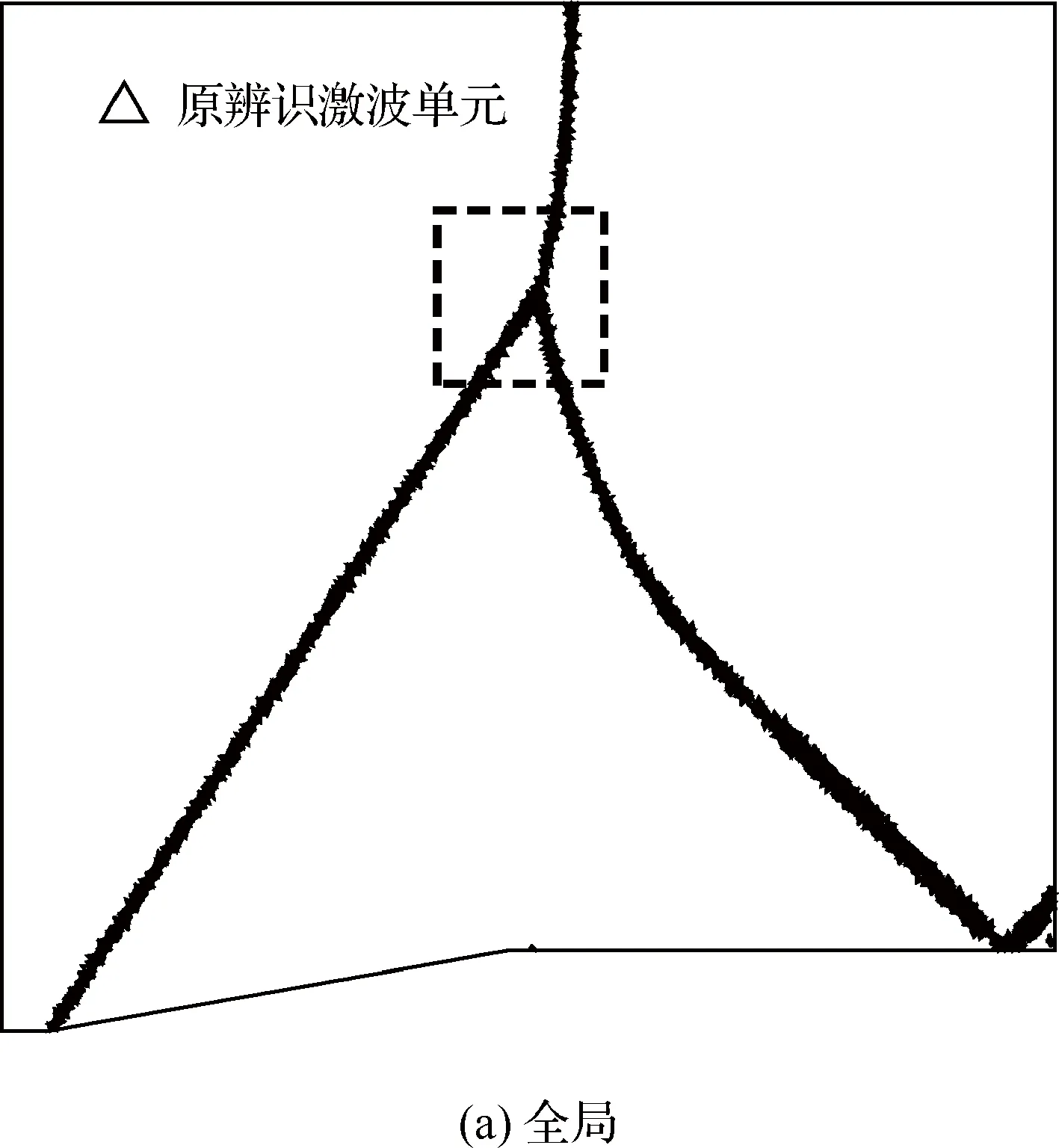
图2 定常激波反射:初始辨识的激波单元
(1)
由于考虑了流向,δp的正、负号分别对应流体处于压缩和膨胀的状态,而激波处通常表现出很强的压缩性,因此首先要过滤掉δp<0的单元。
2) 由于数值计算难免会存在耗散和误差,会造成一些非激波区域的δp值为一个较小的正量,故过滤掉满足式(2)的单元:
δp<ξ1δpmax
(2)
式中:δpmax为流向压强梯度的全场最大值;ξ1为全局滤波系数,当流场中激波的强度比较悬殊时,该系数过大可能会滤掉某些弱激波而导致部分激波带缺失,因此经大量数值试验的调试,取ξ1=0.01。流场中除了激波间断外可能还存在接触间断,由于数值捕捉出的接触间断两侧压强近似相等,因此基于式(2)流向压强梯度阈值法可以有效地过滤掉接触间断。
3) 然而几乎不可能只通过设置满意的ξ1,既能完整地辨识多激波又能去除全部噪声。此外,因全局滤波强度不大,经第2步辨识的激波带可能会出现一些伪激波单元,为了在一定程度上提高辨识方法的普适性,考虑局部特性对满足式(3)的单元进行二次去噪:
(3)

定常激波反射算例经上述方法辨识出的具有一定厚度的“激波带”如图3所示,受激波强弱影响,激波带的厚度并不均匀,通常有2~5层激波单元。由于数值误差的存在,激波带往往存在很多“毛刺”和“空穴”,为了使后续聚类分析更加准确,从两方面对原始辨识的激波带进行了光顺优化。首先一方面标记“空穴单元”为激波单元,另一方面剔除“毛刺单元”。所谓空穴单元是指其所有节点均落在激波带上的初始非激波单元(图3中绿色单元),而毛刺单元是指共面相邻激波单元的个数小于2的初始激波单元(图3中蓝色单元)。

图3 定常激波反射:激波带的优化
1.2 激波单元的聚类分析
聚类分析是一种十分重要的统计数据分析方法,在数据挖掘、模式识别、图像分析和机器学习等许多领域受到广泛应用;它的目标是将数据集分成许多簇,使得同一簇内的数据点相似度尽可能大,而不同簇间的数据点相似度尽可能小[20]。本文采用经典的K-means聚类(K-Means Clustering)[21]算法对优化后的激波带进行聚类处理,下面举例简要介绍该算法对图4(a)数据点的聚类流程:
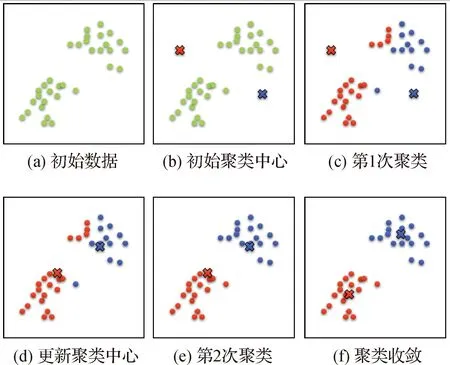
图4 K-means聚类算法示意图
1) 选择K个初始“聚类中心”。在图4(b)中,初始化选择了两个聚类中心,即图中红、蓝“×”形点。
2) 对任意一个数据点,求其到K个聚类中心的“距离”(取欧氏距离),将该数据点归到距离其最近的聚类中心所在的“簇”。如图4(c)所示,所有数据点在经过第一轮遍历后被分为红、蓝标识的两个簇。
3) 利用均值等方法更新K个簇的中心值。此时对当前标记为红色和蓝色的数据点分别求出其新的质心,作为新的聚类中心,如图4(d)所示,红色和蓝色聚类中心的位置发生了变动。
4) 重复步骤2)~3),若所有聚类中心在迭代更新后位置都保持不变,则迭代结束;否则继续迭代。最终得到的两个簇及其聚类中心如图4(f)所示。
K-means聚类算法操作简单,易于实现,且十分高效,一般仅需5~10次迭代即可收敛。但是研究表明,该算法对初始聚类中心的位置选取比较敏感,不同的随机初始聚类中心得到的聚类结果可能差异显著。因此,在对激波单元聚类时,合理的初始聚类中心位置显得至关重要,其既不能偏离激波带过远,也不能分布的过密或过稀。下面介绍下针对激波带初始聚类中心的选取方法。
首先任意选取一激波单元作为搜索起点,以该单元格心为圆心,n倍当地网格尺寸为半径r作“搜索圆”(经大量算例评估,一般n取6~7即可获得合理的结果),如图5所示;随后将格心点落在该圆区域内且未被搜寻到的激波单元归为一簇,计算该簇中所有激波单元格心坐标的平均值,作为新的搜索圆圆心坐标;反复迭代直到所有激波单元均被搜寻到,则所有搜索圆的圆心即为初始聚类中心。

图5 定常激波反射:确定初始聚类中心
取所有激波单元的格心作为数据点集,对所有激波单元进行K-means聚类;经过若干次迭代后最终所有激波单元被划分到不同的簇,如图6所示,为方便显示,紧邻的簇用不同颜色加以区分。
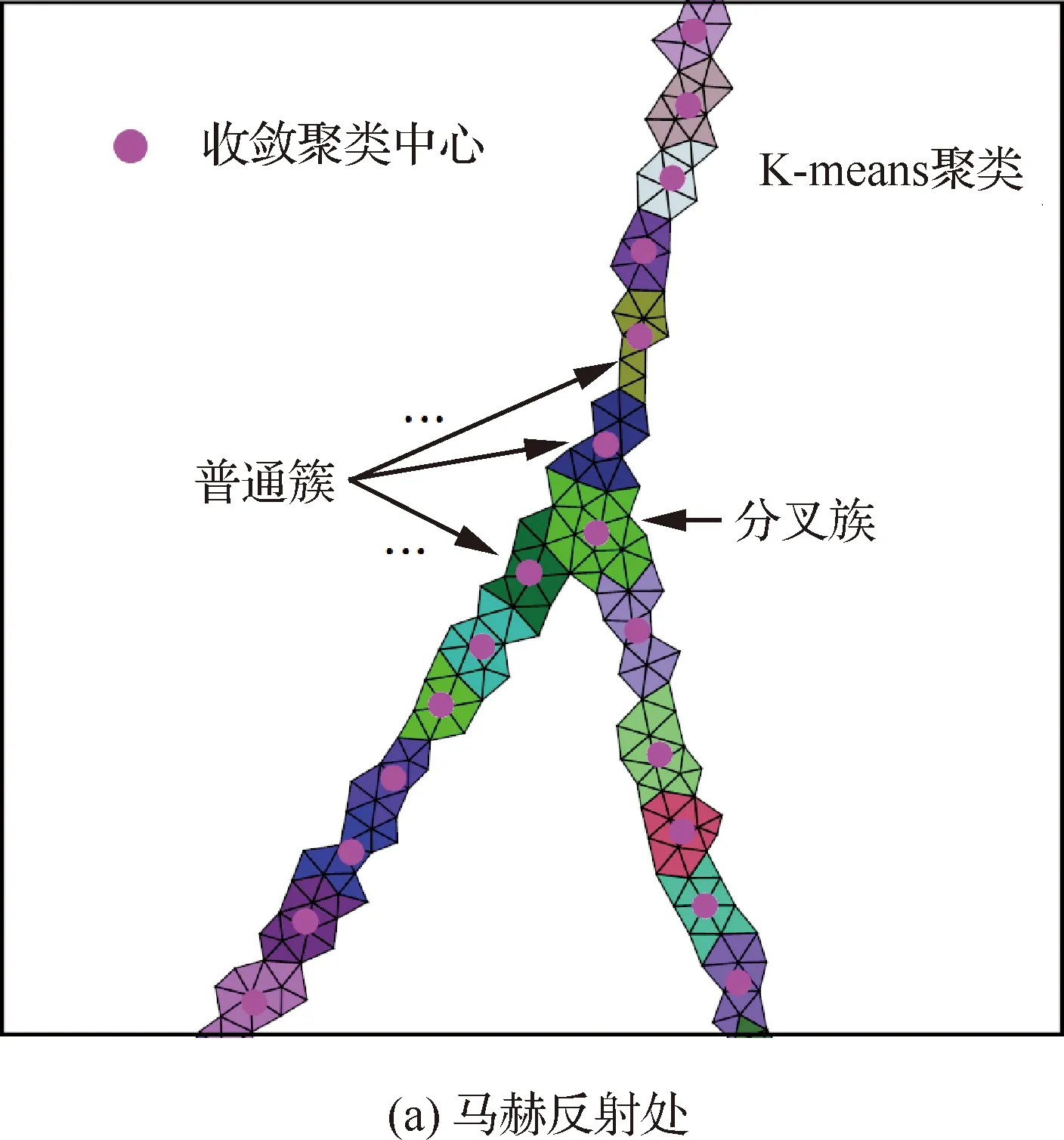
图6 定常激波反射:K-means聚类结果
为了后续便于分析激波拓扑结构及其干扰模式,根据每个簇的相邻特征将簇进一步分成4类:
1) 终止簇。若流场内部某簇仅有1个相邻簇,则该簇为终止簇;其一般位于流场内部激波起始/终止处,注意该簇不与边界相邻。
2) 普通簇。若流场内部某簇仅有2个相邻簇,则该簇为普通簇;其一般呈“串状”普遍分布于激波带中,是数量最多的簇。
3) 分叉簇。若流场内部某簇有3个及以上相邻簇,则该簇为分叉簇;其一般分布于厚度较大的激波带处,如三波点、四波点和弱激波处等。
4) 边界簇。若某簇直接与流场边界相邻,则该簇为边界簇;其通常存在于激波-壁面反射处、壁面拐角处以及流场进出口边界处等。
其中,终止簇、分叉簇和边界簇统称关键簇,其在流场中个数虽少,却往往位于激波拓扑或形状发生变化的关键位置处。
1.3 激波的模式识别与拟合
如何自动准确地辨识出流场中激波干扰点的位置是一个难题。下面通过对激波带K-means聚类得到的各个簇进行“近邻分析”,给出了一种激波模式识别和激波线拟合的策略:
1) 判断是否存在需要进行合并的簇。具体分两方面,若某分叉簇与其他分叉簇相邻,则将这些分叉簇合并;若某边界簇与其他边界簇(注意它们必须对应同一个边界)相邻,则将这些边界簇合并。
2) 若进行了簇合并的操作,需要重新对簇进行分类,并计算新簇的聚类中心。如图6(a)无需进行簇合并,而图6(b)经簇合并后变成图7,即原4个相邻分叉簇合并后形成1个新的普通簇,一同紧靠下壁面的2个相邻边界簇合并后形成1个新的边界簇。

图7 定常激波反射:簇合并后
3) 识别关键激波点。规定若某分叉簇与周边3个簇(见图6(a))或4个簇(见图23)相邻,则该分叉簇对应的聚类中心即为三波点或四波点;若某分叉簇仅与1个簇相邻,则其聚类中心即为激波终止/起始点(见图25);若某边界簇与2个簇相邻(图7下边界处),则取该边界簇对应的边界中心点作为激波-壁面反射点;同理,若某边界簇仅与1个簇相邻(图7右边界处),则边界中心点即为激波-边界干扰点。通过以上近邻分析,便可识别出激波-激波干扰或激波-边界干扰等模式。
4) 记录各条激波所包含的簇。从第3)步得到的某一关键簇开始搜索,依次记录下该分支上两两相邻的所有普通簇,直至搜索到另一关键簇停止,此时该一系列簇即对应一条激波;继续搜索确定下一激波分支上的簇,直到遍历完流场中所有的簇。
5) 拟合激波线。依次连接激波包含的一系列簇所对应的聚类中心,便可得到各条激波线;然而此时得到的激波线可能比较曲折(图7中的白色实线),为此,本文进一步采用著名的Bézier曲线拟合算法[22]获取更加光滑的激波线,下面对其作简要介绍。
当给定一系列有序散点P0、P1、…、Pn时,则其n阶Bézier曲线的一般参数化形式为
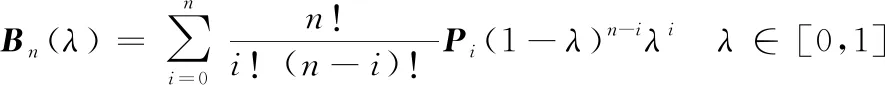
(4)
如4个点对应的三阶Bézier曲线表达式为
B3(λ)=P0(1-λ)3+3P1λ(1-λ)2+
3P2λ2(1-λ)+P3λ3λ∈[0,1]
(5)
式中:Pi称为Bézier曲线的控制点,且该曲线开始于点P0(对应λ=0)并结束于点Pn(对应λ=1)。值得注意的是,Bézier曲线是有方向性的,控制点的次序不同会拟合得到不同的曲线;且Bézier曲线是直线的充分必要条件是所有控制点共线。
因此,根据Bézier曲线的特点,若第4)步记录的某条激波包含n+1个簇,则将两个关键簇的聚类中心分别作为起始点P0和终止点Pn,而将其余依次紧邻的普通簇的聚类中心作为控制点P1~Pn-1,进行n阶Bézier曲线拟合便得到更加光滑的激波线,如图8所示。
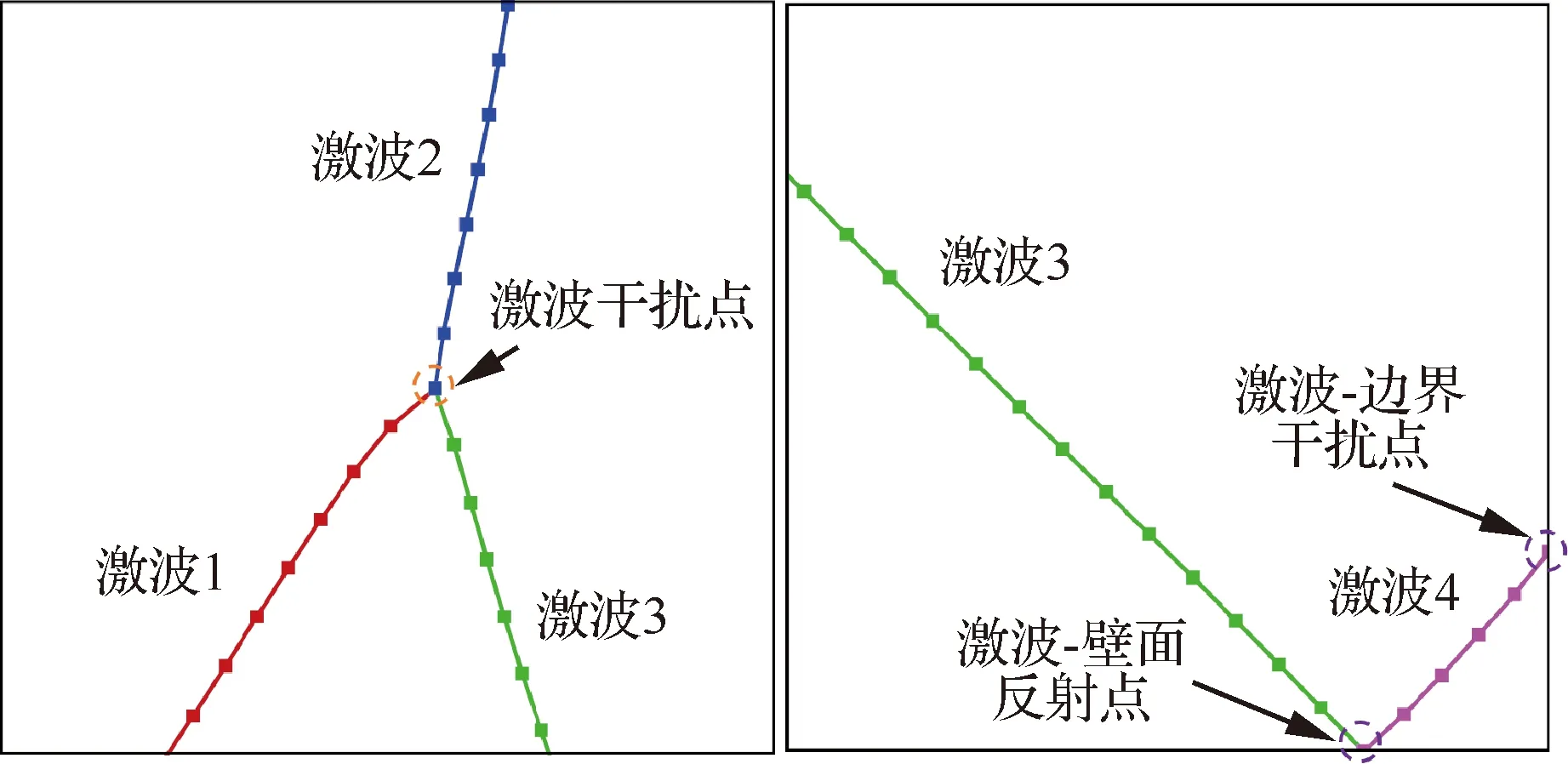
图8 定常激波反射:拟合的激波线
图9对比了最终拟合的激波线与流场压强云图,4条激波线、三波点、激波-壁面反射点和激波-边界干扰点的位置都比较准确,显示出该算法具有良好的有效性和准确性。
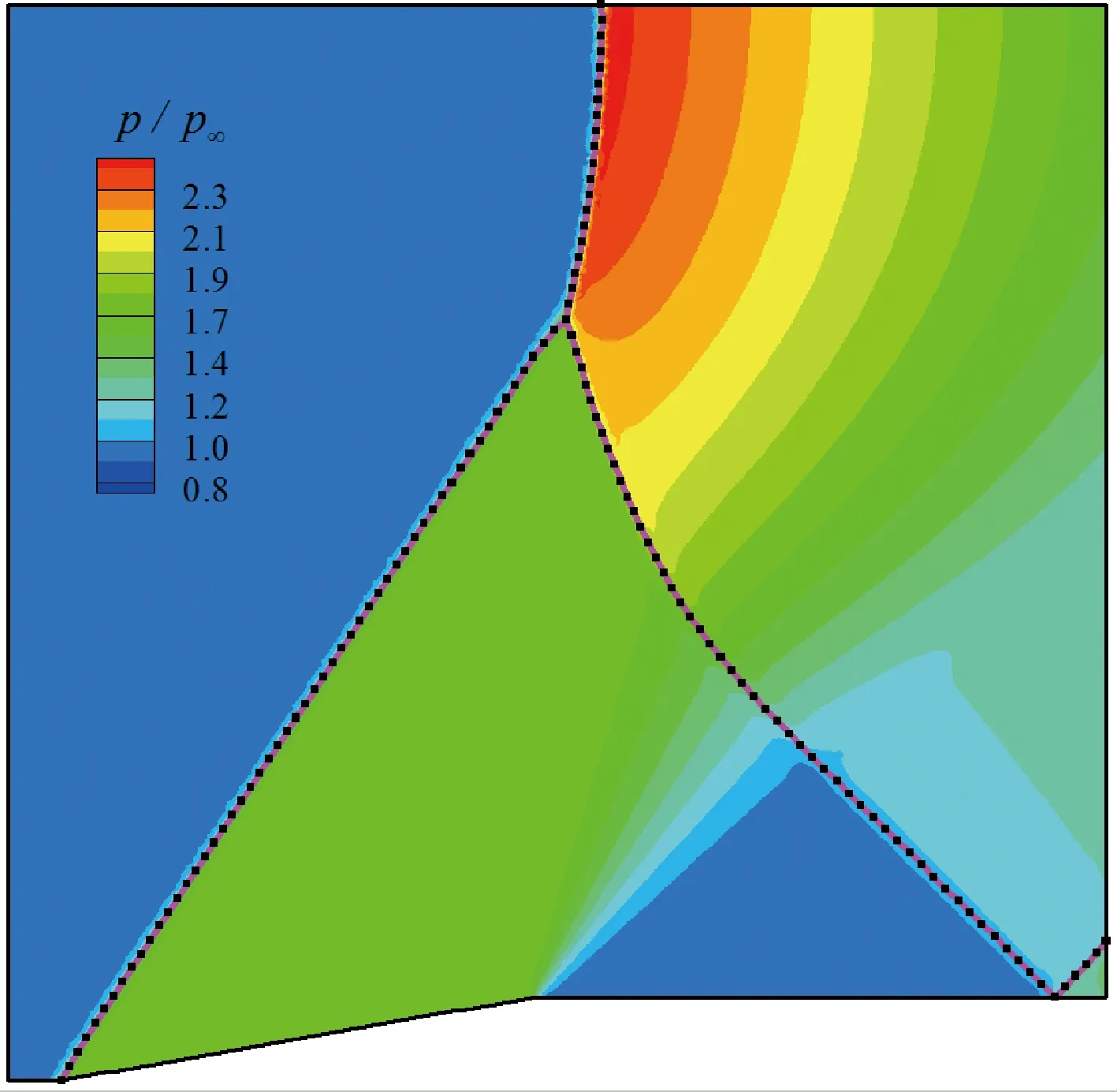
图9 定常激波反射:激波线拟合结果与云图对比
1.4 算法小结
该二维激波模式识别算法的总体流程如图10所示,主要包含激波辨识、聚类分析和识别拟合3方面内容;此三者层层递进,激波辨识是基础,聚类分析是核心,而识别拟合是关键。
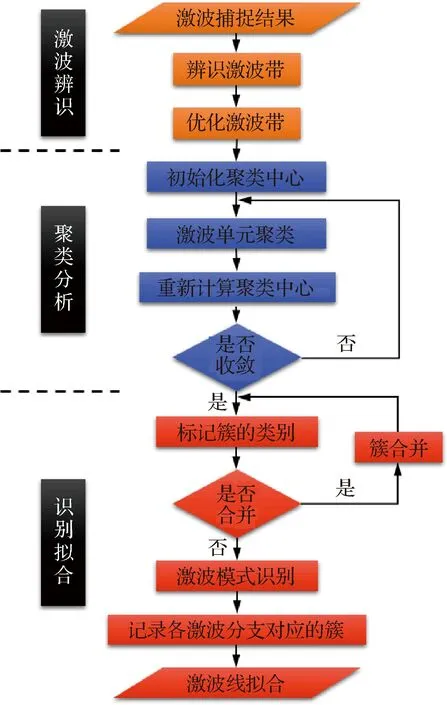
图10 算法流程图
从激波捕捉流场出发,通过流向压强梯度阈值法进行二级滤波辨识提取出具有一定厚度的激波带,到最终准确识别出激波-激波干扰点和激波-边界干扰点等关键位置,且拟合出的各条激波线的形状和位置都具有较高的精度。总之,该算法的最大优势是基本不需要人工参与,且算法简单高效,可以准确实现从“激波带”到“激波线”的拟合识别。
2 算例验证
通过4个超声速流动算例从多方面考察了该算法的准确性、适用性和可靠性。以下激波捕捉流场均基于格心型有限体积法[23]计算,空间对流项通量采用van Leer格式,时间推进采用显式4步Runge-Kutta格式,保证在光滑流场中时空均具有二阶精度,全场均不考虑黏性。
2.1 定常斜激波
首先,采用两种条件下的定常斜激波算例,验证本算法最终拟合出的激波线的准确性。计算区域为x∈[0,L],y∈[0,0.9L],在x=0.1L处存在楔角,均匀超声速来流经过楔面会产生一道笔直的斜激波,上边界为超声速出口,激波不会反射。为了产生相对较弱和较强的斜激波,楔面角θw分别取3°和20°,对应的来流马赫数Ma∞分别为1.469和1.959。计算网格尺寸均为0.02L,全场分别有5 257个和4 472个三角形网格。
两种状态下的斜激波经辨识和聚类分析的结果如图11所示,弱激波辨识出的激波带较宽,最终一共得到25个聚类中心;而强激波辨识出的激波带更加锐利,最终一共得到了22个聚类中心。将这些聚类中心作为控制点按顺序代入式(4)拟合得到Bézier曲线,并与相应的理论值进行对比(图12),可见拟合值具有较高的位置精度。表1进一步对比了激波角,可见无论是弱激波还是强激波,最终拟合出的激波线的激波角度和理论值的相对偏差都不到1%。
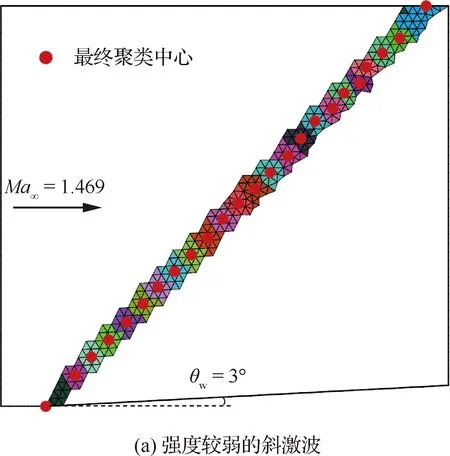
图11 定常斜激波:聚类结果
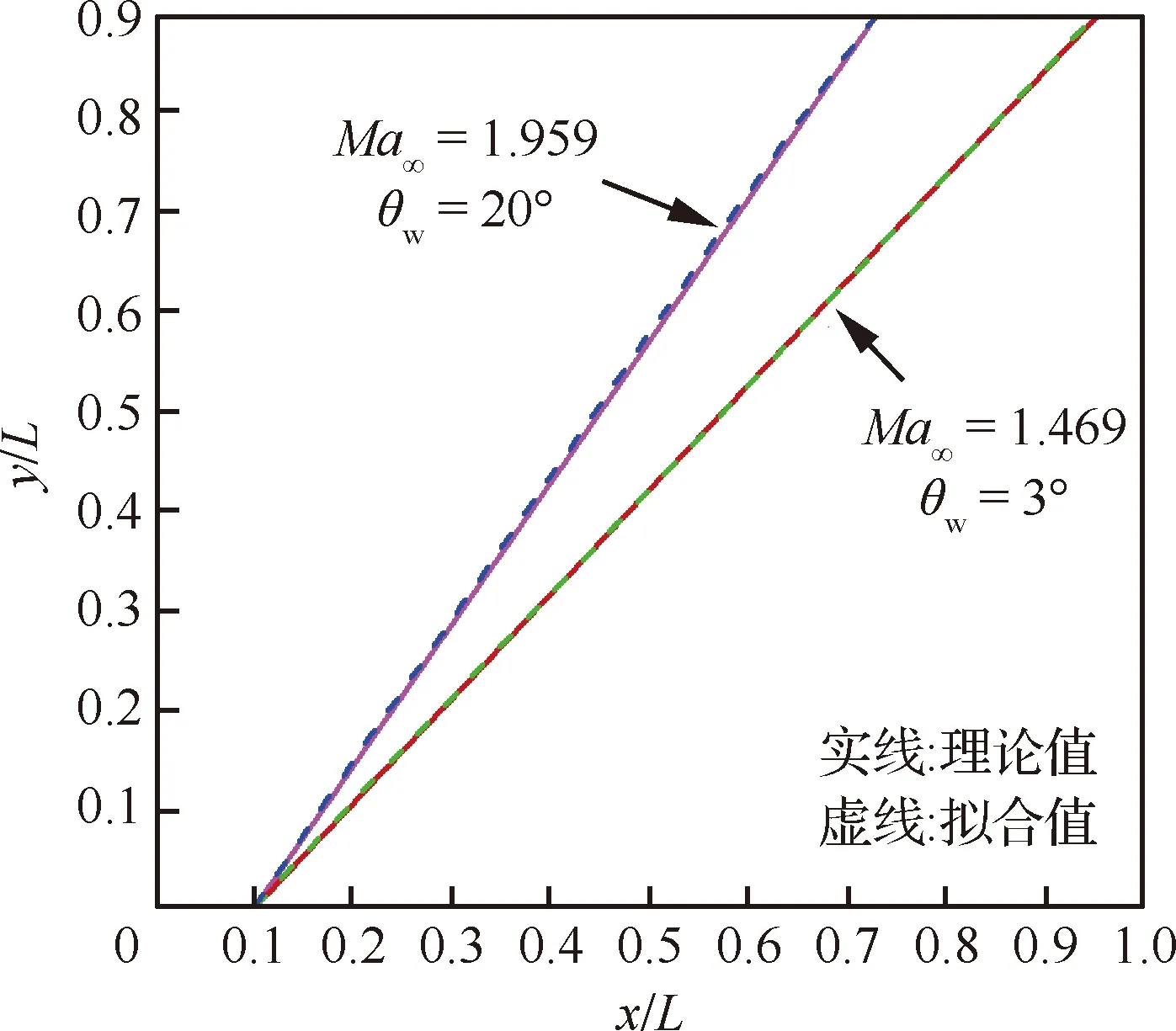
图12 定常斜激波:激波线拟合值与理论值对比

表1 定常斜激波:激波角拟合值和理论值对比
2.2 定常激波反射
仍考虑图1所示的定常激波反射流动,测试本算法对不同类型网格的可靠性。首先分别基于全场均匀的四边形结构网格和三角形/四边形混合网格重新进行数值计算,平均网格尺寸均为0.015L。 图13给出了这两种类型网格下局部流场压强等值线云图(图例与图1一致)。

图13 定常激波反射:不同种类网格下的压强云图
根据1.1节所述的激波探测方法,采用相同的滤波系数,分别获得满足条件的激波带。在对激波单元进行K-means聚类分析时,结构网格算例全场一共确定了64个初始聚类中心,而混合网格算例共搜寻到了82个,经若干步后得到收敛的簇及其聚类中心。此时,根据簇的类别和相邻簇的个数判断某些簇是否需要进行合并,图14和图15分别给出了两种网格下壁面马赫反射处和正规反射处聚类合并后的结果。
图14(a)和图15(a)中各存在一个分叉簇,因其与周围3个激波带分支中的3个普通簇相邻,可以判定该分叉簇的聚类中心位于流场三波点附近。此外,反射激波S3在受到膨胀波干扰后,强度显著减弱;观察图14(b)和图15(b)壁面激波反射处的激波带,其厚度要明显大于三波点附近激波带的厚度,相应地,各簇包含的单元个数也明显增加,但并没有存在错误的分叉簇,且下壁面和出口边界处的两个边界簇都被准确地识别出来。值得注意的是,由于激波-壁面反射点比较靠近出口边界,图14(b)中存在两个边界簇直接相邻的情况,但由于它们邻近的边界不同,因此在簇合并操作中并未错误地将它们合并。
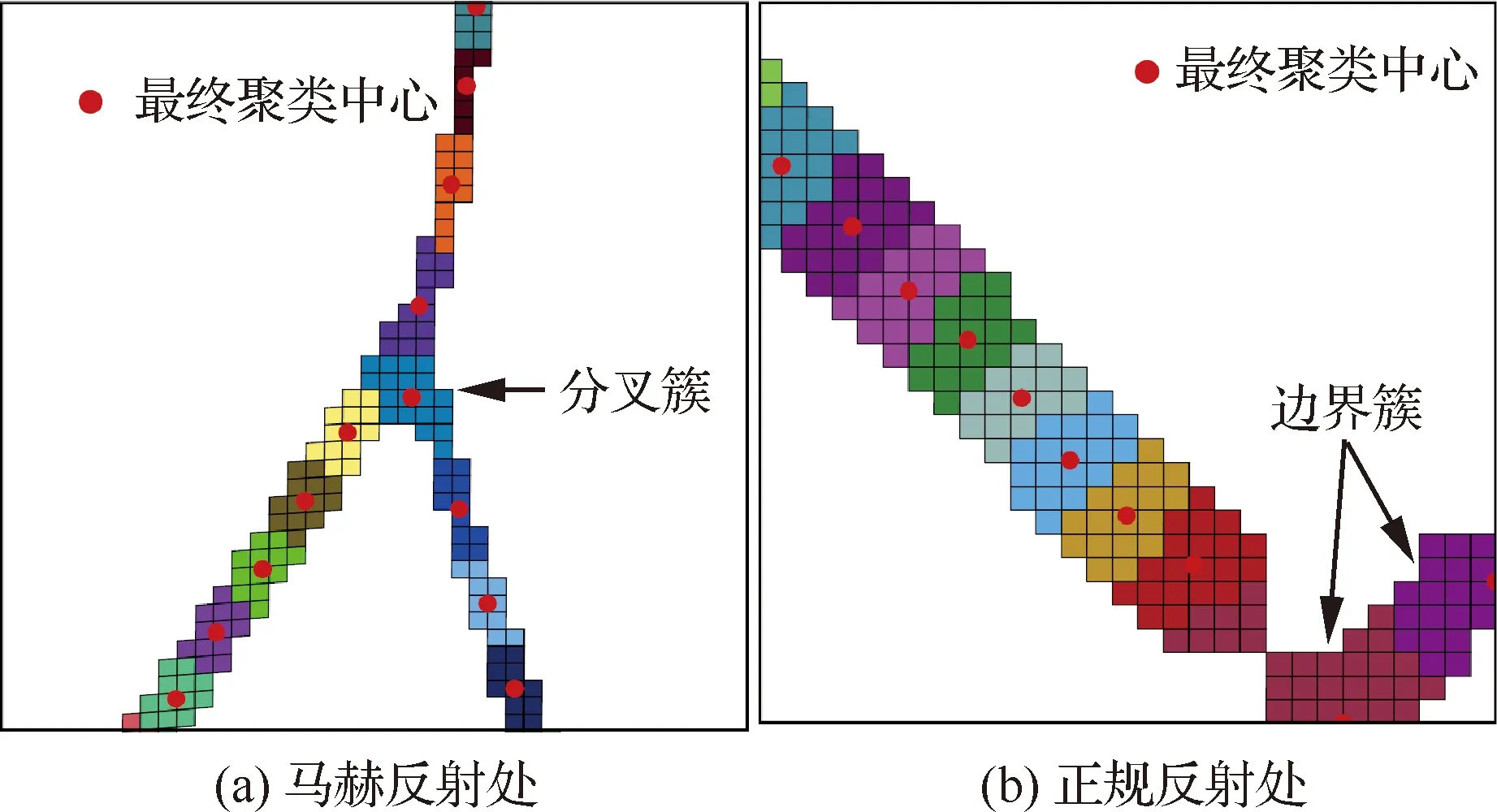
图14 定常激波反射:基于结构网格的聚类结果
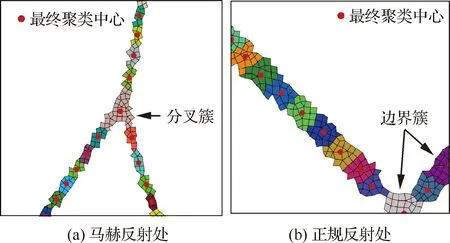
图15 定常激波反射:基于混合网格的聚类结果
以上采用的都是均匀网格,下面进一步考察了本算法在非均匀网格中的适用性。如图16所示,在非结构网格的基础上,沿入射激波的法向进行加密,第一层网格高度为0.002L,向激波两侧各推进5层四边形网格,网格高度增长率取1.2,随后将激波右侧四边形网格沿对角线剖分成三角形网格。图17显示了对辨识出的激波带进行聚类分析后的结果,虽然激波带厚度差异明显,但并不影响分叉簇的位置识别。

图16 定常激波反射:非均匀网格下的压强云图
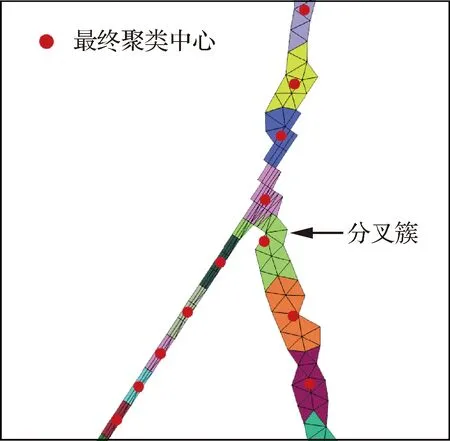
图17 定常激波反射:基于非均匀网格的聚类结果
最后对比了以上3种网格下最终的拟合结果(图18),4条拟合激波线的形状和位置都与数值捕捉的激波吻合得很好;从局部放大图看出,三者拟合出的三波点和边界干扰点位置稍有不同,这是由于流场数值误差和初始激波带辨识差异造成的,难以完全根除,但偏差都在一个网格尺度左右,仍显示出较好的一致性。
2.3 同侧和异侧激波干扰
对波系较为复杂的多激波干扰问题进行了数值验证,几何模型和流场压强等值线如图19所示,全场采用均匀的非结构Delaunay三角形网格离散,平均网格尺寸Δ1=0.015L。Ma∞=3.0的高超声速均匀气流在经过收缩管道时,经上壁面20°楔角压缩产生了一道斜激波S1,与此同时,先后经下壁面10°和20°楔角二次压缩产生了两道斜激波S2和S3,随后S2和S3发生了同侧正规激波相交并汇聚成了一道新激波S4,最终激波S1与S4发生了异侧正规相交并产生了两条透射激波S5和S6。全场一共产生了六道激波,并存在一个三波点和一个四波点结构。

图19 激波干扰:几何模型与压强云图
根据流向压强梯度过滤得到的激波带分布如图20所示,在两个激波干扰处聚集了大量的激波单元。通过进一步增补原激波带外缘两侧的空穴单元,优化后的激波带更加光顺。随后对优化的激波带进行K-means聚类,结果如图21(a)所示,在每条激波带分支中都分布着大量呈串状依次排列的普通簇,而在分支交汇处却聚集着若干分叉簇,这些分叉簇都至少与周围3个簇直接相邻,因此需要进行簇合并操作。
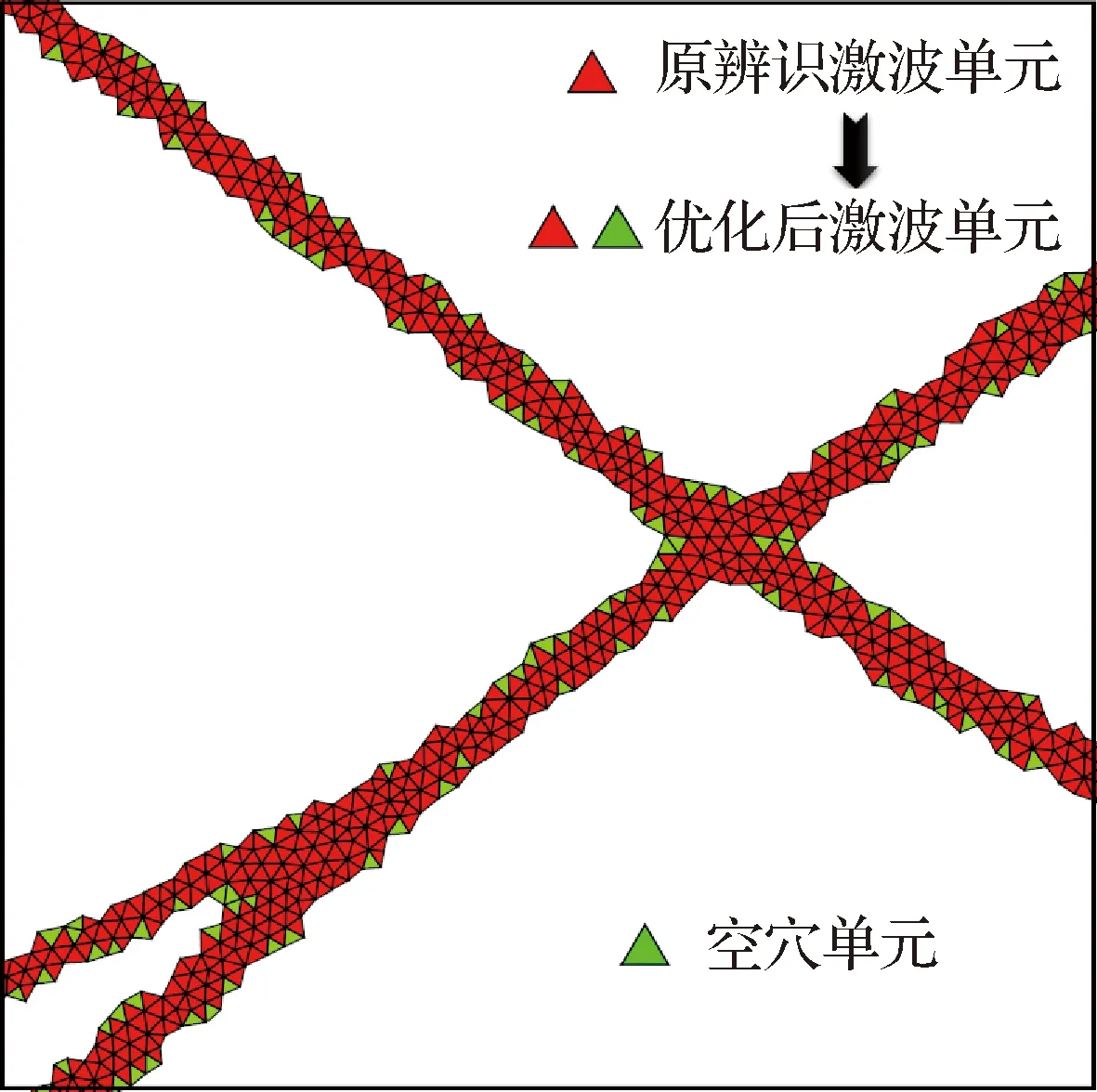
图20 激波干扰:辨识出的激波带
在将某些簇合并后(图21(b)),清晰地存在两个较大的分叉簇,分别与周边3和4个普通簇相邻,因此其聚类中心可以被视为三波点和四波点位置。最终分别将各个分支中的聚类中心进行拟合得到了所有6条激波线,结果如图22所示。拟合的激波线、激波相交点均落在数值捕捉激波的过渡区内,显示出该算法良好的精度。

图22 激波干扰:拟合的激波线
实际上,激波(尤其是激波-激波干扰点)的探测精度在很大程度上取决于流场的分辨率。也就是说,捕捉得到的激波过渡区宽度越小,越有利于精确探测到激波及其干扰点的位置。下面考察了网格的疏密程度对激波探测的影响。
在其他相同计算条件下,仅仅改变流场网格的尺寸,分别设计疏(Δ2=0.02L)和密(Δ3=0.01L)两套非结构网格,重新进行流场计算。经激波辨识、聚类分析和簇合并后的结果如图23所示;网格越稀,划分的簇越少,且聚类中心两两相距越远。图24对比了3种网格尺寸下最终拟合出的激波线,可以发现,三者大部分基本完全吻合,但激波干扰点处差异较大。对于同侧激波干扰结构,由于三道激波的斜率都比较接近,因此当网格较稀时,数值捕捉激波的过渡区较宽,会造成两条入射激波带提前交汇(对比图23中两图可见),分叉簇的位置会发生较大改变,最终造成了辨识出的三波点位置出现较大差异。另一方面,对于异侧激波干扰产生的四波点结构,虽然稀网格对应的分叉簇也较大,但其聚类中心的位置和密网格的结果偏差并不显著。
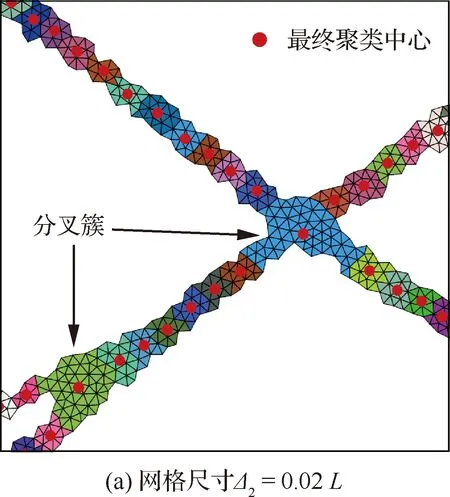
图23 激波干扰:不同网格尺寸下的聚类结果
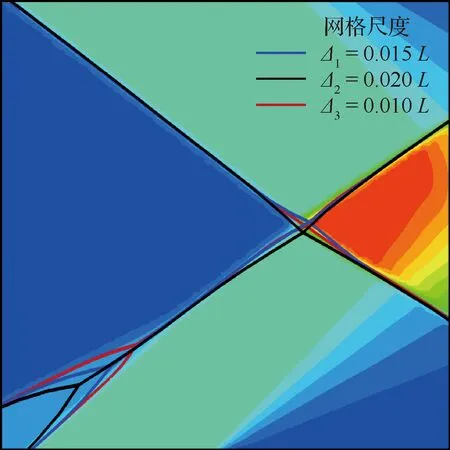
图24 激波干扰:3种网格尺寸下拟合的激波线对比
该算例表明,本文算法对同侧激波干扰点的识别精度网格依赖性相对较强,即网格疏密对结果的影响较大;而对于异侧激波干扰点,包括上文激波反射算例中的三波点结构,其识别精度受网格尺度的影响较小;而对于干扰点以外的激波线,拟合精度受网格尺度的影响最小,始终吻合得比较好。
2.4 前向台阶非定常流动
采用著名的前向台阶超声速绕流算例[24]测试该算法在复杂非定常流动中的有效性。均匀自由来流马赫数Ma∞=3.0,且初始流场取来流参数,通道入口和出口处的高度分别为L和0.8L,台阶高度及其上表面长度分别为0.2L和2.4L。全场采用均匀非结构三角形网格划分,网格尺度为0.01L。本算例中的时间均为无量纲量。
在流场的发展历程中,台阶前首先出现一道向左运动的弓形激波,因其强度较大,当受到上壁面干扰时会发生反射,并从运动正规反射逐渐过渡到马赫反射;而反射激波又从下壁面反射回上壁面,最终在管道壁面形成了4次激波-壁面干扰(Shock-Wall Interaction,SWI)。此外,气流在台阶拐角处发生过度膨胀,过膨胀气流会与下壁面相撞形成一道相对较弱的孤立斜激波,该激波最终与第一道反射激波发生异侧正规相交,相交后的弱激波又与第二道反射激波汇聚形成同侧激波-激波干扰(Shock-Shock Interaction,SSI)结构。
图25依次给出了5个关键时刻的辨识激波带的聚类结果,通过二次滤波,在辨识出运动强激波的同时,那道较弱的孤立斜激波也被很好地提取出来;此外,图25(d)和25(e)中并没有错误地将三波点处的接触间断提取出来。随后,通过聚类分析和簇合并操作,可以准确地定位分叉簇与边界簇的位置,从而清晰地识别出各个时刻流场激波的总个数及相互干扰的模式(如SWI或SSI)。
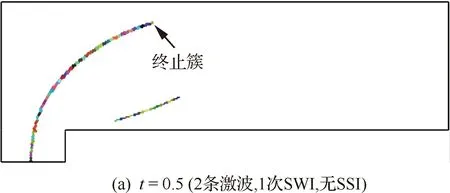
图25 前向台阶绕流:不同时刻激波带的聚类结果
以两时刻为例,图26定性比较了最终拟合出的激波线与流场压强云图。可以发现,不仅各条近似直线的反射激波位置准确,而且台阶前的大曲率弓形激波也与捕捉激波吻合得很好,反映了该算法对各种形状激波的拟合都具有较好的可靠性。在得到不同时刻的拟合激波线后,可以方便地将其在同一张图中显示出来,进而有利于分析激波的演化过程,深化对运动激波干扰的认识。从图27可以看出,相比激波-上壁面干扰点,台阶后的激波-下壁面干扰点向左移动的速度更快;且弓形激波在上壁面反射形成的马赫干扰的长度在迅速增大;而在t=1.5时刻后,弓形激波的位置变化比较缓慢,三波点近似沿弓形激波向下滑动。
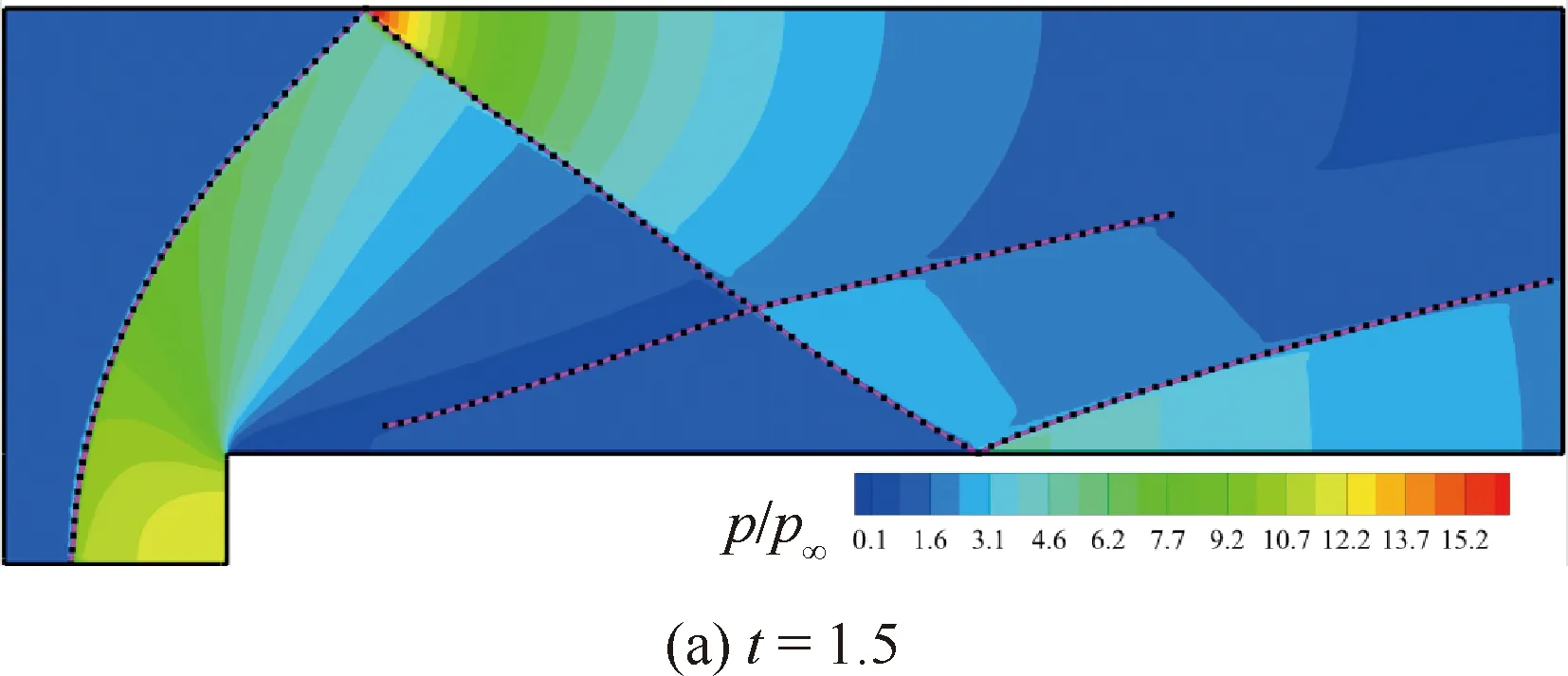
图26 前向台阶绕流:拟合的激波线与压强云图对比
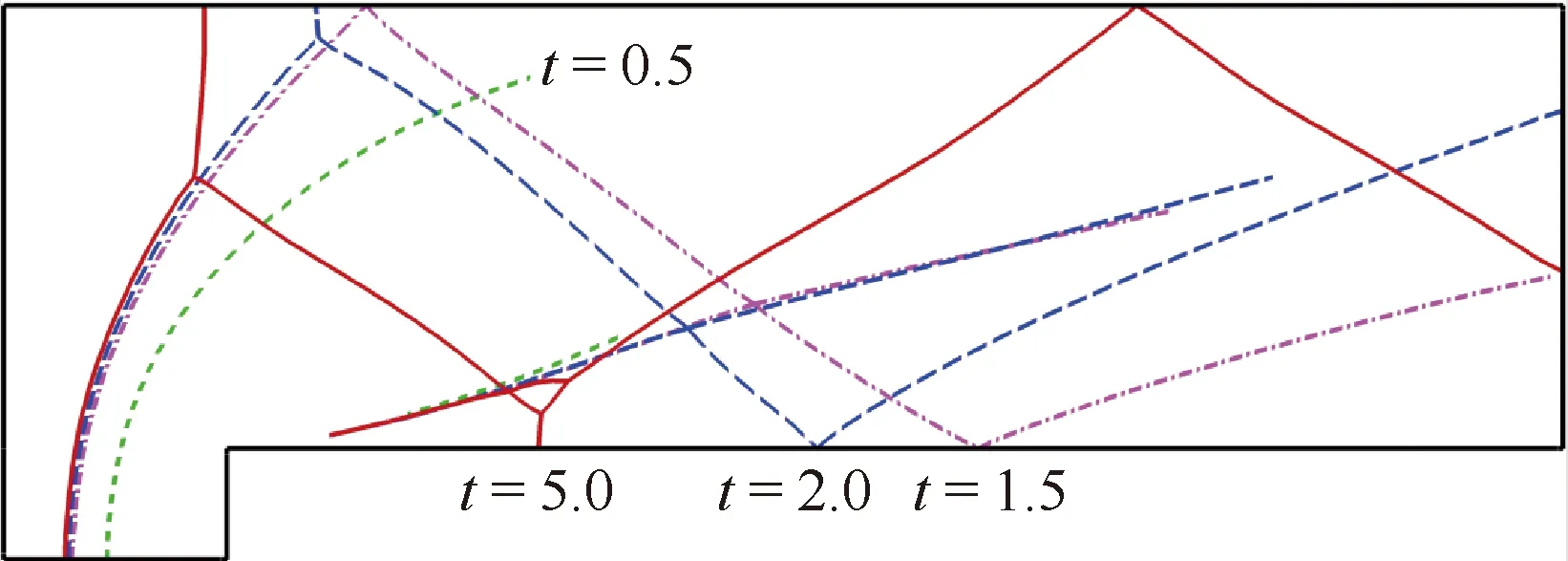
图27 前向台阶绕流:4个时刻拟合的激波线
3 结 论
1) 该算法在传统基于流场当地参数进行激波探测的方法基础上,对提取的激波单元进一步处理;先后结合K-means聚类算法和近邻分析成功实现了激波干扰点的准确定位;最后采用Bézier曲线算法拟合得到各条质量较高的激波线,数值试验表明激波线的大部分位置与形状受流场网格疏密影响不大。
2) 对于同侧激波干扰,干扰点的位置受流场本身分辨率的影响较大,密网格下一般会获得更为精准的结果;而对于异侧激波干扰,其干扰点的识别结果通常比较准确,且网格依赖性不强。
3) 该算法自动化程度较高,基本不需要人工干预,且适用于任意网格类型,对复杂非定常流场中的运动激波辨识也具有良好的可靠性和准确性。
总之,该面向全局的激波探测算法可以有效识别出更为精确的激波拓扑结构,未来可以用于CFD中某些对激波位置有特殊需求的技术中,例如激波装配[16-19]、网格自适应[25]、流场特征可视化[26]等。由于三维激波相交干扰结构比较复杂,将该方法推广到三维是今后努力的方向。
