基于pade逼近的重心有理混合插值新方法

胡枫 安徽理工大学 数学与大数据学院 安徽淮南 232001

引言

重心有理混合插值近些年来越来越成为了研究的热门领域之一,在这些研究中重点关注于重心插值与Thiele连分式,newton和lagrangian插值多项式的相互混合,同时提出了分叉连分式重心混合有理插值方案来处理二元插值问题.在本文中,通过选择合适的权函数构造计算简单同时没有极点和不可达点的重心有理插值,在每个插值节点处与被插值函数相应的pade逼近进行组装建立一种新的重心有理混合插值,与重心Thiele型混合有理插值和重心有理插值相比,能达到更高的逼近精度,误差更小.

1.重心有理混合插值新方法

有理函数rn(x)当ωi≠0时满足插值条件

在1988年berrut通过选取合适的权函数

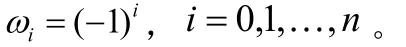
建立了无极点且便于计算的重心有理插值,下面考虑对被插值函数f展开成形式幂级数

定义有理函数

是由形式幂级数决定的 [m / n]阶pade逼近式,其中 Pm(x)是次数不超过m的多项式, Qn( x)是次数不超过n的多项式,且满足 Qn( 0 )=b0=1.各项系数算法如下所示

由上可知有理函数 )(xA 与被插值函数的前 nm+次形式幂级数展开在 0=x 处完全相等,即

于是我们构造基于pade逼近的重心有理混合插值新方法如下

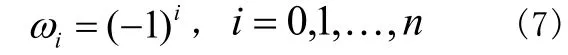
2.数值例子

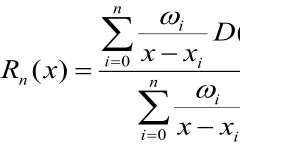
定义在 ]1,0[ 的实值函数

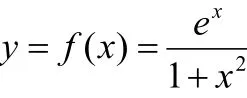
为了便于讨论,选取10个插值节点如下

对应函数值有

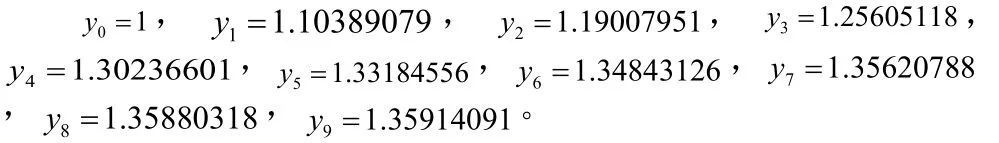
由上述插值数据构造满足插值条件的重心有理插值,重心Thiele型混合有理插值和本文中提到的在插值节点处基于pade逼近重心有理混合插值新方法 )(xR , )(xr , )(*xr 如下所示:

重心有理插值

重心Thiele型混合有理插值

其中 )(xA 是Thiele型连分式插值

基于pade逼近的重心有理混合插值新方法

为了能直观的比较各种插值方法的逼近效果,现使用matlab2014a绘制原函数图像和各类插值误差函数图像如下图1-4所示,

图1 原函数 )(xf 的图像

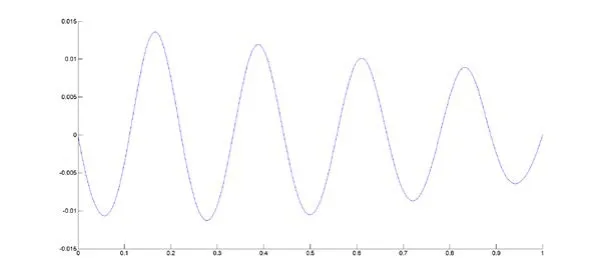
图2 重心有理插值 )(xR 的误差函数图像

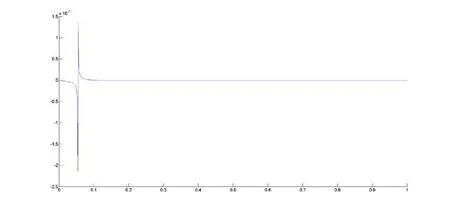
图3 重心Thiele型混合有理插值 )(xr 的误差图像

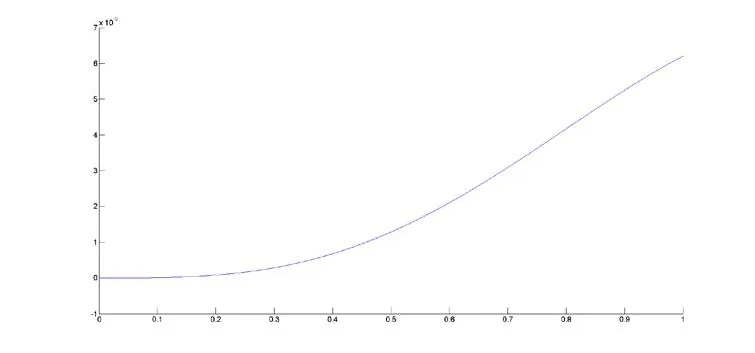
图4 基于pade逼近的重心有理混合插值 )(*xr 的误差函数图像

结论

本文研究一类基于pade逼近的重心有理混合插值新方法,通过选择恰当的权函数,在插值节点处将被插值函数的pade逼近式与重心有理插值进行组装构造新的重心有理混合插值算法,该方法不仅没有极点且与传统重心有理插值和重心Thiele型混合有理插值比较,无需计算插值节点处的函数值,计算更加简洁,误差更小,逼近效果更加优越.