基于数学思想视角下的分类讨论教学研究
2020-05-21张燕
张燕


[摘 要] 在初中数学教学实践中,以引导学生实现不同知识点的综合运用与组合为目标,探究基于数学思想视角下的分类讨论教学策略具有重要的意义. 文章以“圆周角”教学为例,探究了初中数学教学中渗透分类讨论思想的策略.
[关键词] 初中数学;数学思想;分类讨论
思想是数学的精髓,而在解决的问题较为复杂、不能单一分析时,就要应用分类讨论思想,这种思想不仅能够帮助学生正确处理各种不确定性问题,而且也有利于各种数学思维的形成[1],然而,在日常初中数学教学实践中,相当数量的学生在分类讨论过程中频频出现重复、遗漏讨论事项的现象,因此,以引导学生实现不同知识点的综合运用与组合为目标,探究基于数学思想视角下的分类讨论教学策略具有重要的意义.
基于数学思想视角下的分类讨论教学策略
1. 呈现背景,低起点导入
分类讨论思想与其他知识和技能的获得一样,均是源于实际生活,因此,教师应摆脱教科书的束缚,降低起点,以基础知识为主要载体,鼓励学生从日常现实生活中概括和抽象出分类讨论思想,运用形式化的数学符号和文字,使实际问题上升为数学思想[2].
2. 展开讨论,确定分类标准
教师应对题目所呈现的数据和运算条件进行周密的研究,思考题目中蕴藏着的隐含条件;然后应用转化、讨论思维,采用分割的方式,将一个较为复杂的问题逐渐分解成为多个简单的子问题,并在展开讨论时要最大限度地注重讨论的方向和深度不能超越所选分类的界限. 最后,为了减少学生分层讨论时层次乱套、重复遗漏事项的现象,教师应在小组分类讨论时,统一分类讨论的标准.
3. 深入理解,确认分类方式
在数学题目呈现之后,教师应通过“还有没有其他想法”“如果是这样了”等追问的方式引导学生准确挖掘出题目中所隐含的可能性,按照自己确定的数学逻辑关系进行分类讨论. 值得说明的是,教师应帮助学生树立信心,不能被题目中呈现的未知数的数量所干扰,要按照某种逻辑关系厘清所有的知识点,并且在分类时做到细心和耐心.
4. 小组合作,加强论述深度
教师应充分尊重每个学生在分类讨论中的意见,提升不同学生在不同分类方法中的应用经验. 同时,在组织学生小组讨论时,应尽可能地不限制或少限制学生的交谈范围,可以以某一突破口不断对分类思路进行查缺补漏,也可以选择先自己独立分类再采用相互交流意见的方式进行.
基于数学思想视角下的分类讨论教学实践
纸上得来终觉浅,仅有相关分类讨论教学策略是不够的,而基于数学思想视角下的初中分类讨论教学应是理论与实践相结合. 在初中数学教学实践中,相当数量的学生对于圆周角与圆心角概念相互混淆,并且圆周角在判定相似三角形,证明角度、线段相等方面具有重要的作用. 因此,笔者以初中“圆周角”教学为例,深入探究初中数学教学中如何渗透分类讨论教学思想.
1. 创设情境,导入新课
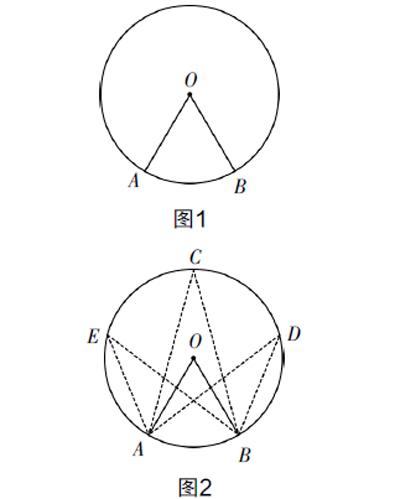
依据“最近发展区”原则,可充分利用多媒体呈现如图1所示的图形,鼓励学生仔细观察,并从角度、弧度等方面引导性地帮助学生思考∠AOB有哪些特点和性质,引导学生温故已学知识圆心角的概念和性质. 随后,呈现如图2所示的图形,创设如下的教学情境,即在某海底游乐园中,点O,C,D,E为甲、乙、丙、丁四个游客所的位置,试问:从数学的角度分析,站在哪个位置能够从圆弧形玻璃AB处看到海底内部更多的景物?从而结合日常情境设置一个悬念,引出本节课程所学知识——圆周角.
2. 合作探究,学习新知
仍以创设的情境——图2为例,要求学生独立思考∠ACB,∠ADB,∠AEB这三个角之间的共同特征,引导学生明确圆周角的特点. 以小组为单位,学生类比以前已经掌握和熟悉的圆心角概念,归纳概括得出“圆周角”的概念,并要求学生思考圆周角与圆心角概念之间的区别和联系,独立完成表1.
然后,呈现如下的变式题目(如图3),要求学生利用圆周角的概念,说明该图形是否是圆周角. 对于是圆周角的,要求学生重复圆周角判定的条件;对于不是圆周角的,要求學生说明理由. 同时,利用题目渗透分类讨论思想,结合前面的教学,进一步帮助学生完善知识结构,归纳总结出圆心角与圆周角之间的三种不同位置关系,即圆心在圆周角的一边上、内部和外部三种情形.
3. 观察实验,测量比较
在明确圆周角概念之后,教师还应引导学生探究圆周角的性质[2]. 在具体实践中,教师应让学生以小组为单位,要求学生在纸上任意绘画一条弧AB所对应的圆周角和圆心角,如图4、图5、图6所示.
然后引导学生思考如何应用所学技能测量出圆周角和圆心角的角度,并指导学生应用量角器测量完成表2中的数据,鼓励学生从数值的角度猜测圆心角与圆周角之间的等量关系. 值得说明的是,对于未发现圆周角和圆心角规律的小组,教师应发挥主导作用,引导他们从位置、角度等方面发现规律. 对于已经发现规律的小组,教师应鼓励他们反思探究过程,思考如何从数学语言的角度准确表达出自己的猜想.?摇
4. 验证猜想,深化思想
在上述测量比较、充分讨论的基础上,教师应随机邀请一组,要求本小组阐述探究过程中出现的疑惑或问题,本小组最终归纳和总结出的规律. 然后,渗透信息技术教学,充分利用几何画板中的动态图像功能直观演示,从而有效验证上述所得猜想. 最后,为了培养学生严谨的数学思维,教师要求学生根据探究过程写出已知和未知条件,并通过圆心O在∠ACB上、内部和外部三种情况进行验证.
以验证圆心O在∠ACB上为例,如图6所示. 因为OC=OB,所以∠B=∠C. 因为∠AOB是∠BOC的外角,所以∠AOB=∠C+∠B,所以∠AOB=2∠ACB,即∠ACB=∠AOB.
同理,教师还应指导学生应用从特殊到一般的思想,要求学生以小组为单位继续验证圆心O在∠ACB内部和外部两种情况.
5. 反思感悟,总结提升
在学生经历圆周角定理探究之后,教师应以本节课程中的收获为主题,要求学生总结和完善自己的知识结构,并以课前所设置的悬念为主题,反过来要求学生继续思考课前提出的问题,然后应用圆周角定理,得到只有站在O处的位置,观察A,B两点的视角最大,其余C,D,E的位置,由于均为圆周角上的一点,所以其观察效果是一样的.
值得说明的是,在上述组织学生学习圆周角的过程中,主要采用引导发现、合作探究的形式,其中圆周角与圆心角三种位置关系属于图形位置不确定而引起的分类讨论. 纵观初中数学教学过程,其分类讨论思想还体现在以下几个方面:一是由于题目中字母的不同取值、位置的不同而引起的讨论;二是由于限制条件不同而引起的讨论;三是计算时受实施条件的限制而引起的讨论. 在具体教学实践中,教师应让学生以小组为单位,鼓励思维严密完整的学生带动思维水平较低的学生,从而实现“兵教兵”的效果;并且还可以应用一些经典范例,结合课堂小结、单元总结概括提炼出分类思想,促使学生不断增强思维的严密性[3].
结语
总之,基于数学思想视角下的分类讨论思想不是一朝一夕就能在教学中渗透的,教师应在具体数学教学过程中,以数学知识为载体,采用低起点、频追问、小组合作的方式不断渗透数学思想方法,只有这样,才能不断提升学生解题能力、思维能力,改善学生学习的技巧、方法,深刻理解数学的内涵,促进学生的数学素养的提升.
参考文献:
[1]潘楷佳. 例谈分类讨论数学思想方法的教学策略[J]. 中学数学,2019(14).
[2]马军. 分类讨论思想让初中数学教学更精彩[J]. 数学教学通讯,2018(08).
[3]张雪梅. 关注几何图形的多样性 凸显分类讨论思想——分类讨论思想在解题中的应用及思考[J]. 中学数学,2014(08).
