含裂纹梁的模态与振动疲劳寿命分析

2020-05-19马一江陈国平沈超明

江苏科技大学学报(自然科学版) 2020年2期

马一江,陈国平,沈超明,杨帆

(1.江苏科技大学船舶与海洋工程学院,镇江 212003)(2.南京航空航天大学航空学院,南京 210016)

作为工程中应用最广泛的结构件,梁结构的健康监测问题逐渐成为工程中的研究热点．在高温、高压以及宽频激励环境中服役的梁结构,通常存在不同程度的结构损伤．结构损伤大多以裂纹的形式出现,在振动环境中疲劳裂纹会不断扩展,引起梁结构的失稳破坏,最终导致机械设备发生突然性的破坏．为避免机械设备发生疲劳破坏,必须对服役中的梁结构进行健康监测．

目前,在含裂纹梁模态分析方面,国内外学者提出了很多有效的方法．文献[1]中通过有限元方法将含呼吸裂纹悬臂梁的非线性振动转化为分段线性系统,计算各段线性区域的固有频率．文献[2]中利用无质量弯曲弹簧模拟横向裂纹,通过传递矩阵方法研究裂纹对悬臂梁固有频率的影响．文献[3]中通过功率平衡原理的Ritz级数法推导含裂纹简支梁的模态,并通过实验进行验证．文献[4]中将开口裂纹简化成横截面的折减,通过摄动理论推导含多条裂纹梁特征模态参数的理论公式．传递矩阵方法不需要推导出含裂纹梁模态的解析解,且适用于各种不同边界条件的梁结构．因此,传递矩阵法的应用范围更加广泛．

在2000年左右,关于含裂纹梁疲劳寿命预测问题引发了学术界的研究热潮．文献[5]中采用现象学方法描述了含裂纹沥青混凝土梁的疲劳破坏规律．文献[6]中通过位错分布来模拟裂纹,评估裂纹尖端应力强度因子对梁结构疲劳寿命的影响．文献[7]中假设在每个振动循环中裂纹处的名义应力保持不变,采用静力学方法预估含裂纹梁的疲劳寿命．然而,在振动过程中裂纹尖端应力场的变化非常复杂,静力学方法模拟裂纹处的应力场并不完全符合实际情况．因此,通过动力学方法模拟裂纹尖端应力场逐渐成为学术界的研究热点．文献[8]中通过梁结构局部柔度模拟裂纹,采用传递矩阵方法分析裂纹对梁结构自由振动的影响．文献[9]中采用Paris公式[10]模拟裂纹的扩展速率,研究阻尼损耗因子对裂纹梁振动疲劳寿命的影响．文献[11]中在共振状态下研究外激励频率对应力强度因子和裂纹扩展速率的影响．文献[12]中将航空发动机叶片简化为悬臂梁结构,采用接触有限元法研究裂纹梁振动与裂纹扩展的耦合问题．当裂纹处于悬臂梁根部时,文献[13]中采用线弹性扭转弹簧和拉压弹簧模拟裂纹,分析外激励频率和阻尼比对悬臂梁振动疲劳寿命的影响.文献[14]中建立含裂纹悬臂梁有限元模型,通过时域法和频域法研究阻尼比对裂纹梁振动疲劳寿命的影响．由于悬臂梁根部区域任意位置均有可能出现初始结构损伤,为预估含裂纹梁的振动疲劳寿命,根部区域的初始裂纹是不可忽略的影响因素．

文中用无质量弯曲弹簧来等效横向张开式裂纹,弹簧刚度由横向裂纹相对深度决定．基于Euler-Bernoulli梁理论,推导出含裂纹悬臂梁的特征方程,分析裂纹参数对悬臂梁各阶模态的影响．在每个振动循环中,考虑裂纹梁振动与疲劳裂纹扩展的相互作用,假设裂纹面的应力均保持不变,采用Paris方程表征疲劳裂纹的扩展速率．设定合理的失效判据,采用同步分析法预估含裂纹悬臂梁的振动疲劳寿命．

1 理论模型

1.1 含裂纹悬臂梁模型

文中的研究对象为一个矩形等截面悬臂梁结构,如图1(a)，其几何参数:长度为l、高度为w、厚度为b．在梁上任意位置有一条横向初始裂纹,距离悬臂梁固定端的距离为lc．假设该结构横向裂纹是张开式裂纹(在梁结构振动过程中裂纹始终保持张开状态),并且该横向裂纹的初始深度为a．

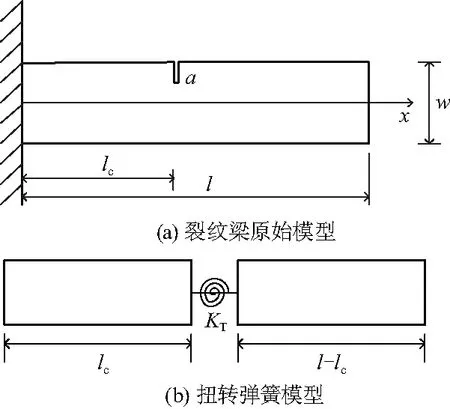
图1 含裂纹悬臂梁Fig.1 Cantilever beam with a crack

图1(b)中,初始裂纹为横向裂纹,含裂纹悬臂梁可以离散为由无质量弯曲弹簧连接的完整悬臂梁和两端自由梁结构,并且弯曲弹簧的刚度与横向裂纹引起的局部柔度直接相关．对于梁结构上存在横向裂纹的情况,文献[15]中提出了裂纹局部柔度模型,并推导出横向初始裂纹在梁结构上引起的局部柔度变化和无质量弯曲弹簧的刚度可以表示为:

(1)

式中:αc为横向裂纹引起梁局部柔度;KT为无质量弯曲弹簧的刚度;w为横向裂纹所在梁横截面高度;I为横向裂纹所在横截面的惯性矩;rc=a/w为该横向裂纹的相对深度;f(rc)为横向裂纹的无量纲局部柔度函数,E为弹性模量；I为梁结构横截面的惯性矩，可以通过应变能密度函数来求解:

f(rc)=0.627 2rc2-1.045 33rc3+4.594 8rc4-

9.973rc5+20.294 8rc6-33.035 7rc7+

47.106 3rc8-40.755 6rc9+19.6rc10

(2)

式中:rc≤0.6．

1.2 模态分析

图1中，含裂纹悬臂梁为等截面Euler-Bernoulli梁,则Euler-Bernoulli梁的振动微分方程为:

(3)

式中:ρ为悬臂梁结构材料的密度；A为梁结构的横截面面积．

在初始外激励作用下,悬臂梁结构进行自由振动．通过分离变量法,Euler-Bernoulli梁的固有振动为:

y(x,t)=Y(x)sin(ωt)

(4)

将式(4)代入式(3),可以推导出Euler-Bernoulli梁的振型函数:

Y(x)=c1sin(λx)+c2cos(λx)+

c3sinh(λx)+c4cosh(λx)

(5)

通过分离变量法将Y(x)分离出来,可以得到:

(6)

根据材料力学理论,梁结构横截面转角θ、弯矩M和剪力Q的表达式:

(7)

将式(6、7)结合起来,推导出:

将上述方程组转化为矩阵形式,推导出每段梁左右两端横截面的关系:

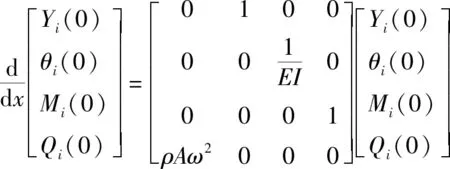
(8)

(9)

式中:Li为每段梁的长度．

假设每段变截面梁左右两端截面的传递矩阵为Ti,则可以得到：

(10)

将式(10)代入式(9),可以得到:

(11)

将式(8)代入式(11),推导出每段梁左右两端横截面传递矩阵的表达式:

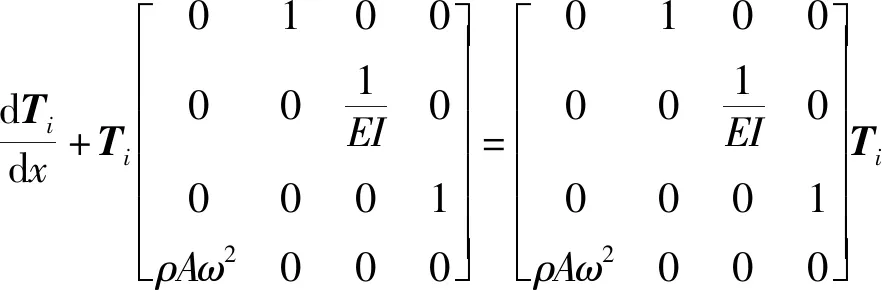
(12)

在每个横向裂纹位置,根据裂纹左右表面的连续性条件,可以得到裂纹左右表面的挠度、转角、弯矩以及剪力的关系式:

(13)

式中:S为横向裂纹左右表面的传递矩阵,且

对于含裂纹悬臂梁结构,左右两端挠度、转角、弯矩和剪力的关系式:

(14)

式中:H为含裂纹梁结构左右两端横截面的传递矩阵,且H=T2ST1．

根据悬臂梁的边界条件,悬臂梁左端横截面的挠度和转角为零,且右端横截面的弯矩和剪力为零[16]:

(15)

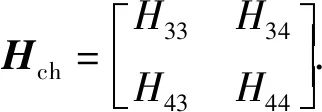
detHch=0

(16)

2 动应力分析

2.1 裂纹悬臂梁振型函数

在动应力分析过程中,假设含裂纹悬臂梁自由端受到横向简谐激励F0eiω1t的作用,则悬臂梁自由端的剪力为F0eiω1t．含裂纹悬臂梁的边界条件为:

(17)

对方程组(17)进行求解,可以推导出第一段梁根部的弯矩M1(0)和剪力Q1(0)．再与Y1(0)=0θ1(0)=0联立,可以推导出简谐激励作用下,第一段悬臂梁的模态振型函数为:

Y1(x)=c11sin(λ1x)+c12cos(λ1x)+

c13sinh(λ1x)+c14cosh(λ1x)

(18)

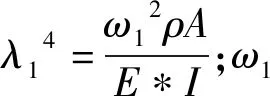
2.2 正应力

在工程实践中,最常见的裂纹类型为宏观张开型裂纹．同时由裂纹引起的机械设备疲劳失效事故中,50%以上由张开式裂纹引起．因此,文中的研究对象是张开型裂纹．根据HOOKE定律:

(19)

在裂纹处(x=lc),裂纹位置的正应力表达式为:

σmax=E*y[-λ12c11sin(λ1lc)-λ12c12cos(λ1lc)]eiω1t+

E*y[λ12c13sinh(λ1lc)+λ12c14cosh(λ1lc)]eiω1t

(20)

3 振动疲劳分析

3.1 裂纹尖端应力强度因子

在裂纹尖端区域,应力会出现奇异性,因此应力不能用来表征裂纹尖端区域的应力场．而裂纹尖端的应力强度因子是有限值,工程中通常采用应力强度因子KI反映裂纹尖端应力场的强弱分布．文献[17]中推导出动应力强度因子的表达式:

(21)

式中:ΔKI为裂纹尖端动应力强度因子的幅值;Δσd为每个振动周期内裂纹截面处动应力幅值:

Δσd=σmax

(22)

f(ζ)为裂纹尖端应力强度因子的几何修正因子,它与裂纹类型和外载荷加载形式密切相关[18]:

f(ζ)=1.122-1.4ζ+7.33ζ2-13.08ζ3+14ζ4

(23)

3.2 疲劳裂纹扩展速率

在线弹性断裂力学范围内,在中等应力状态下且平均应力很低时,使用Paris公式能较好的描述直裂式裂纹的疲劳扩展速率．Paris公式的表达式[19]为:

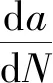
(24)

式中，C,n为材料常数．

由于裂纹类型为宏观张开型裂纹,属于直裂式裂纹．因此,采用Paris方程来模拟振动环境中疲劳裂纹的扩展速率:

(25)

3.3 疲劳裂纹扩展分析

在振动环境中,含初始裂纹结构件会进行受迫振动,使得疲劳裂纹逐步扩展;同时,疲劳裂纹深度和位置的变化引起结构的刚度变化,从而导致结构的动态特性发生改变．因此,疲劳裂纹的扩展与含裂纹结构的振动存在相互影响和相互作用．

文中采用同步分析法,使得含裂纹悬臂梁振动分析与疲劳裂纹扩展寿命估算同时进行．假设在每个循环中,裂纹所在横截面的动应力幅值保持不变．通过式(25)对每个振动循环进行积分,推导出每个振动循环之后横向裂纹所产生的疲劳扩展增量．采用叠加法来计算疲劳裂纹的深度,即将每个振动周期裂纹的扩展增量进行叠加:

(26)

式中:a0为初始状态时疲劳裂纹的深度；Δaj为经过第j次循环载荷之后的疲劳裂纹产生的扩展增量；i为含裂纹梁所经受的总振动循环次数；a为经历i次周期载荷之后疲劳裂纹的总深度．

对式(25)积分,可推导出常幅值载荷激励下每个振动循环疲劳裂纹扩展增量为:

(27)

振动循环的增量为:

ΔNj=Nj-Nj-1,j=1,2,…,i

(28)

考虑到ΔNj很小(文中取ΔNj=1):

(29)

因此,在每个振动循环产生的疲劳裂纹扩展增量表达式为:

(30)

3.4 含裂纹梁断裂临界状态

随着疲劳裂纹的逐步扩展,含裂纹悬臂梁将达到失稳断裂的临界状态,文中设定了3个临界状态来判定含裂纹悬臂梁发生疲劳断裂:

临界状态1:在周期载荷的作用下,随着疲劳裂纹的逐步扩展,如果横向疲劳裂纹扩展至悬臂梁的中性面时,则可以判定悬臂梁结构已经发生失稳破坏．

a≥ac

(31)

式中:ac=w/2，为临界裂纹长度．

临界状态2:在周期载荷的作用下,随着疲劳裂纹的逐步扩展,悬臂梁横向裂纹尖端的应力强度因子逐渐增大．如果裂纹尖端应力强度因子达到悬臂梁材料的断裂韧性时,则可以判定悬臂梁结构已经发生失稳断裂．

Kmax≥Kc

(32)

式中:Kmax为裂纹尖端的最大应力强度因子；Kc为悬臂梁材料的断裂韧性．

临界状态3:在周期载荷作用下,随着疲劳裂纹的逐步扩展,悬臂梁刚度逐渐减小导致悬臂梁第一阶固有频率也逐渐减小．如果悬臂梁的第一阶固有频率下降5%时,则可以判定该梁结构发生失稳破坏[20]．

ω1,i/ω1,0≤95%

(33)

式中:ω1,i为第i次循环后裂纹梁的第一阶固有频率;ω1,0为含初始裂纹时梁结构的第一阶固有频率．

3.5 振动疲劳寿命预估流程

考虑裂纹梁振动与疲劳裂纹扩展的相互作用,采用同步分析法使得含裂纹梁的模态分析与疲劳裂纹扩展同步进行．根据预设的3个临界状态,预估含裂纹悬臂梁的振动疲劳寿命．则在振动环境中,含裂纹悬臂梁振动疲劳寿命预估的流程如图2.

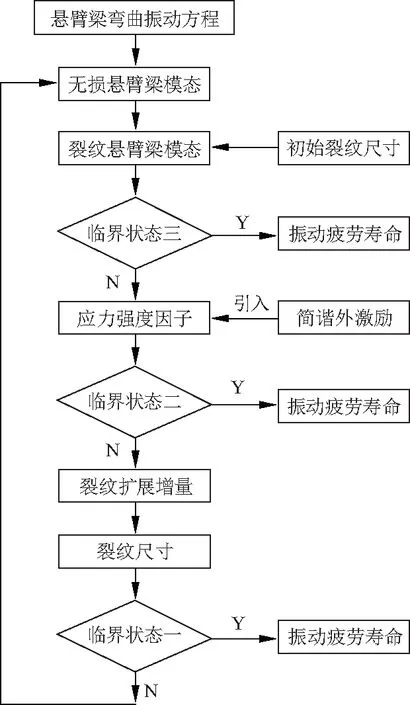
图2 悬臂梁振动疲劳寿命预估流程Fig.2 Flow chart for predicting vibration fatigue life of the cantilever beam

4 结果与讨论

文中的研究对象为含裂纹悬臂梁结构,假设结构的几何尺寸为:l=0.3m、w=0.02m、b=0.002m;结构材料为AISI1050低碳合金钢[21],材料参数为E=210 GPa、ρ=7 860 kg/m3、σb=723.45 MPa、Kc=1 172.2 MPa·m1/2、v=0.33、γ=0.05、ΔKth=0.934 21 MPa·m1/2．试验常数为C=3.009 3e-32、n=3.3．初始裂纹深度a0=0.002 m;计算步长取ΔN=1周;激励幅值为50 N,保持不变．

4.1 裂纹参数对固有频率的影响

图1为含裂纹悬臂梁结构,假设悬臂梁上横向裂纹几何尺寸:裂纹相对深度a/w∈[0,0.5],裂纹相对位置lc/l∈[0,1]．在裂纹的几何参数不同时,推导出含裂纹悬臂梁的前五阶固有频率如图3．

如图3,横向裂纹的存在对悬臂梁结构前五阶固有频率的影响非常大．对于悬臂梁的第n阶模态,存在n-1个模态节点;在各阶模态的节点位置,裂纹深度的变化对悬臂梁对应阶固有频率的影响很小,可以忽略不计．在各阶模态的非节点位置,裂纹深度对悬臂梁的对应阶固有频率的影响则非常大,不能忽略．随着横向裂纹相对深度的逐渐增大,裂纹在悬臂梁上引起的局部柔度逐渐增大,导致悬臂梁结构的各阶固有频率逐渐减小．

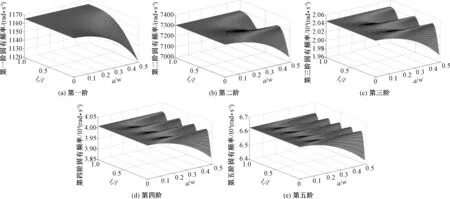
图3 含裂纹悬臂梁前五阶固有频率的三维变化趋势Fig.3 3D changing trend map of the first five orders natural frequencies of the cracked cantilever beam

4.2 裂纹参数对固有振型的影响

选取悬臂梁结构的裂纹几何参数:lc/l=0.2,a0/w=0.4．则含裂纹悬臂梁与无裂纹悬臂梁前五阶固有振型对比,如图4．

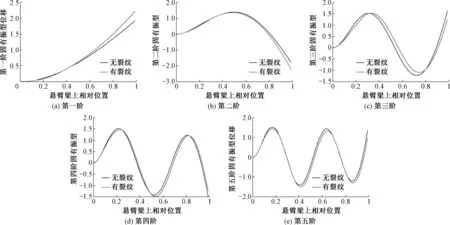
图4 悬臂梁前五阶固有振型对比Fig.4 First five orders mode shapes comparison of the cantilever beam

由图4可知,裂纹的存在对悬臂梁低阶固有振型的影响很大,对高阶固有振型的影响很小．由于裂纹的存在,在裂纹位置悬臂梁的抗弯刚度减小,使得裂纹前后两段梁结构的转角出现微小差异,从而导致悬臂梁前五阶固有振型发生变化．

4.3 裂纹参数对疲劳寿命的影响

在工程实际中,悬臂梁结构经常受到宽频简谐激励的作用，使得悬臂梁结构发生共振．而在悬臂梁结构的各阶共振模态中,第一阶模态的影响最大．因此,文中假设外激励频率追踪含裂纹悬臂梁的第一阶固有频率,使得含裂纹悬臂梁始终处于共振状态．通常情况下,悬臂梁的疲劳破坏发生在固定端区域,选取悬臂梁根部区域的裂纹几何参数(lc/l∈[0,0.1],a0/w∈[0.05,0.1])进行研究．当疲劳裂纹的几何参数不同时,悬臂梁结构的振动疲劳寿命如表1．