多约束条件下焊接桁架结构多优化方法组合设计

刘 川,王 逊,陈维奇,赵 勇

(江苏科技大学 材料科学与工程学院, 镇江212003)

随着科技和社会的发展,工程机械趋于向复杂化、高承载和轻量化的设计要求发展．桁架结构作为工程机械的主要承载部件,常用于大跨度的厂房[1]、展览馆[2]、体育馆和桥梁[3]等公共建筑中． 桁架结构具备轻盈、跨度大、用钢量省、受力体系简单、全部都是二力杆单元、施工方便、建设速度快的特点．对于复杂桁架结构,如国家体育场的桁架结构[4]、上海世博文化中心的钢屋盖结构[5],不同形式结构的作用也不尽相同,因而桁架结构的设计在桁架结构生产施工中起着至关重要的作用．

传统的设计方法,如通过经验公式进行强度验算的方式已不适应当前复杂化、多要求的桁架结构设计．基于计算机技术的优化设计方法应运而生,已经广泛应用于桁架的结构设计，如船用自动扶梯桁架的有限元分析设计[6]、有支撑钢框架离散型拓扑优化设计[7]、桁架式门机结构系统动态优化设计[8]等．以上的例子采用不同的优化设计方法,如有限元分析法[9]、拓扑优化法[10]、遗传算法[11-12]和渐进结构优化法[13]等,其各有利弊．但大多数的优化设计仅利用一种设计方法,未全面考虑相关因素,如强度和质量比值、材料利用率等．文中结合多种优化设计方法,基于ANSYS Workbench针对多约束条件下一种小型焊接桁架结构进行设计,最终获得承载能力高、质量轻、结构合理、生产方便的桁架结构．

1 结构设计要求和优化设计思路

1.1 设计要求

选用低碳钢材料圆杆,设计空间桁架焊接结构,要求结构总质量不超过0.2 kg,高度不低于160 mm,必须保证上部有一个固定面积不低于400 mm2的承力面,考查桁架结构件的承载能力．

1.2 优化设计思路

设计分为3步:① 基础结构的选择．定义棱与底面夹角为θ,考虑承载面积条件下,以等直径杆和等质量简单结构为基础,采用有限元法进行失稳分析,计算出不同截面形状结构最大临界失稳载荷随θ的变化曲线,最终获得最优的截面形状和θ；② 在基础简单结构上添加横杆和斜杆，考虑高度条件,以基础结构的最大变形位置添加横杆,考虑焊接的便捷性以及相同位置施焊容易造成结构局部变形和应力集中,提出材料利用比的概念设计各层斜杆位置；③ 质量和杆径优化，利用拓扑优化法和响应曲面优化法,满足最大承载能力条件下,分析结构减质位置和合适的杆径．以上的每一步设计都以最大失稳临界载荷作为设计目标,最终获得满足承载面积、高度、质量等约束条件下,达到最大承载能力目标的焊接桁架结构．整个结构的设计优化思路如图1．这种逐级优化的设计思路,可以得到满足设计要求的最大承载力和质量的合理设计．

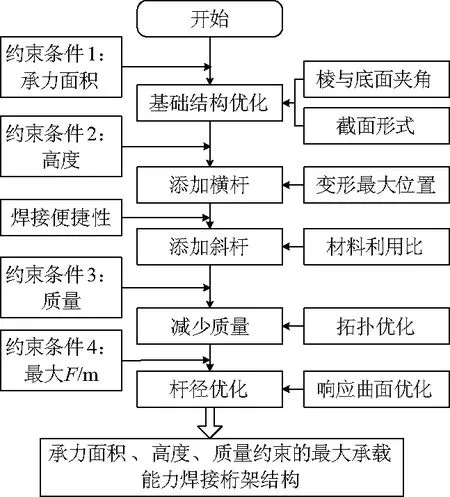
图1 总体设计思路Fig.1 Overall design idea

2 设计结果及讨论

2.1 基础结构选择

截面形状选择正三角形、正四边形、正五边形和正六边形4种形式,设计如图2(a)，仅包括支撑杆和上下承力面的简单结构,该4种结构的上部承力面面积一致(400 mm2),高度相同(160 mm)．考虑两种情况:① 所有杆件的直径都为3 mm;② 4种结构质量相同(杆径不同)．改变棱边与底面的夹角θ,如图2(b),采用ANSYS Workbench进行屈曲分析,计算结构的临界失稳载荷,得到各结构的临界失稳载荷F随θ的变化曲线(图3)．

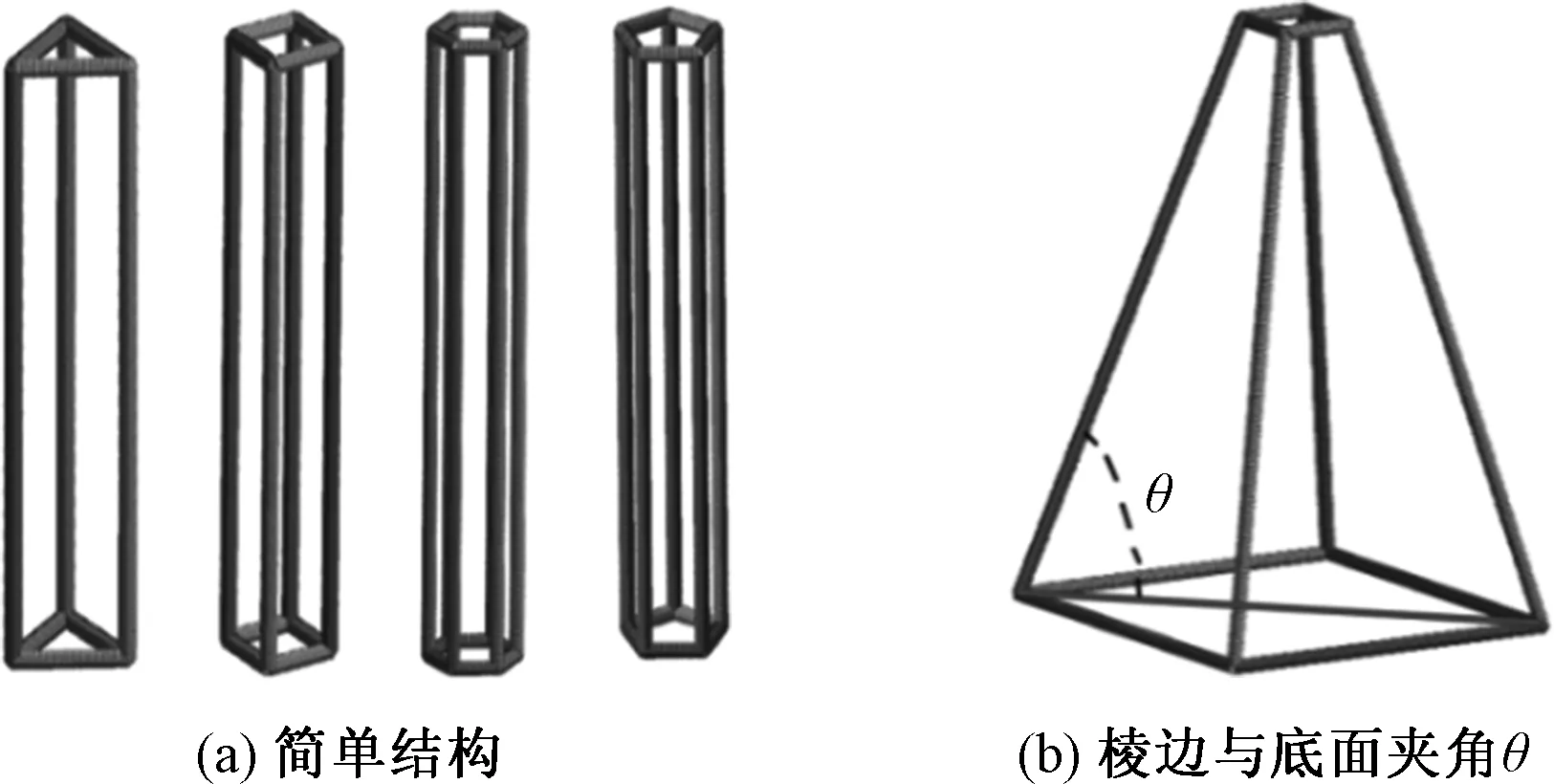
图2 基础结构示意Fig.2 Schematic diagram of foundation structure

由图3可以看出,综合考虑杆件直径和结构质量的情况下,θ达到80°～90°之间时,4种结构的临界失稳载荷F达到最大值．其中,横截面为正四边形结构且θ为83°时的临界失稳载荷最大．结构的质量以及棱边与底面的夹角对桁架结构的稳定性起着主要作用,质量、角度相近的桁架结构的稳定性也相近．横截面面积不变,杆径直径一致的情况下,横杆越多,承载力越大．在质量一致的情况下,横杆越多,其直径越小,降低结构承载能力．因此桁架基础结构形式确定为正四边形棱台,棱边与底面的夹角为83°．

图3 结构临界失稳载荷与θ的关系Fig.3 Relationship between critical buckling load and θ

2.2 添设横杆

将基础正四边形斜台最下端的横杆暂时去除,在Workbench中进行结构静力分析和屈曲分析,得到结构的变形,杆件最大变形位置即为横杆添加位置．对添加横杆后的结构进行屈曲分析,找到变形最大位置继续添加横杆．重复上述步骤直到基础桁架结构添加了4层横杆．如果继续添加横杆,会增加整个结构的质量,并且让杆件分布过密,焊接难度也会增大,添加4层横杆后的结构如图4．

图4 添加4层横杆后的结构Fig.4 Structure after adding 4 layers of transverse rod

2.3 添设斜杆

斜杆形式主要有“Z”字形和“彡”字形．通过有限元计算发现,模型尺寸条件相同情况下,“Z”字形斜杆承载能力优于“彡”字形斜杆连接方式,因此文中以“Z”字形结构为基础进行斜杆位置优化．为了便于分析,设计过程中定义两个变量．设斜杆与横杆在支撑杆上的焊点之间的距离为d．为了方便设计和计算,该斜杆的另一端焊点位置距上一层横杆焊点的距离也设为d(图5)．定义计算的临界失稳载荷除以该层斜杆的总长度为斜杆的利用比η．

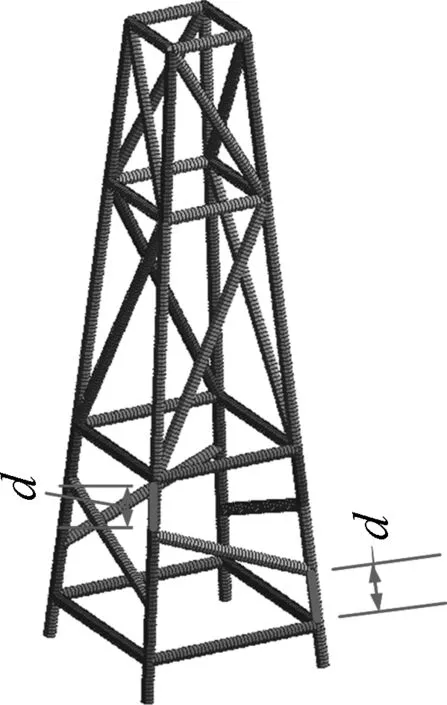
图5 设计变量d示意Fig.5 Schematic diagram of design variable d

采用逐层斜杆优化方法进行设计,从底部第1层开始优化,利用ANSYS Workbench有限元计算分析得出临界失稳载荷F—d和利用比η—d变化图．各层F—d和η—d变化曲线如图6．

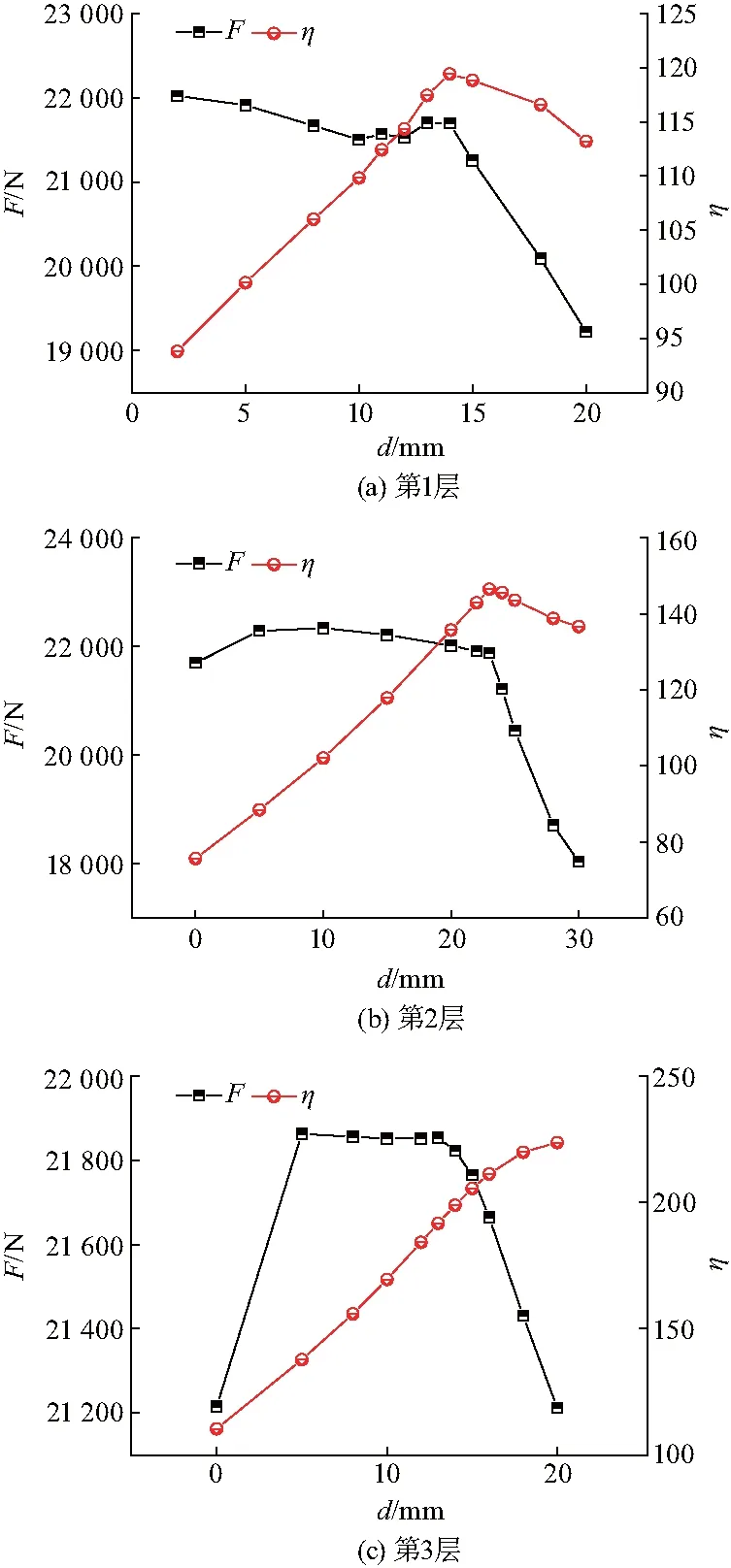
图6 临界失稳载荷F—距离d和利用比η—距离d曲线Fig.6 Curve critical buckling load F to distance d and curve of utilization ratio to distance d

图6中可知,第1层斜杆添加位置最优的点应该是利用比η最大的点,即d为14 mm．该斜杆位置也是承载力和质量配置最合理的点,这样就解决了斜杆位置优化问题．第2层利用比η最大的点为d=23 mm．第3层承载力F最大以及利用比η较大的点为d=14 mm．最终得到的结构如图7．

图7 最终设计结构Fig.7 Final desiged truss structure

经过上述的优化设计得到的最终结构的质量为0.089 4 kg(各杆件直径为3 mm),理论临界失稳载荷约21 823 N,质量不足0.2 kg．随着杆的直径增大,模型的临界失稳载荷和质量也会随之增大,如当杆件直径为5 mm,质量为0.248 4 kg(大于0.2 kg),临界失稳载荷为107 100 N．需要进行进一步的优化以在总质量小于0.2 kg的条件下使得结构承载力最大化．

2.4 拓扑优化减少质量

拓扑优化[10]是一种根据给定的负载情况、约束条件和性能指标,在给定的区域内对材料分布进行优化的数学方法,是结构优化的一种．使用ANSYS Workbench对结构进行拓扑优化,利用SolidWorks做出三维模型,在桁架上端添加一个压板模拟压头,如图8(a)．在压头上施加100 kN的载荷,因考虑到焊接添丝增重的情况,将质量优化减少到0.15 kg．拓扑优化结果如图8.结果表明，横杆和斜杆为质量可减少的区域，即横杆和斜杆的直径可以减小．但拓扑优化无法准确得到优化尺寸,因此需要进一步的优化确定各杆径尺寸．

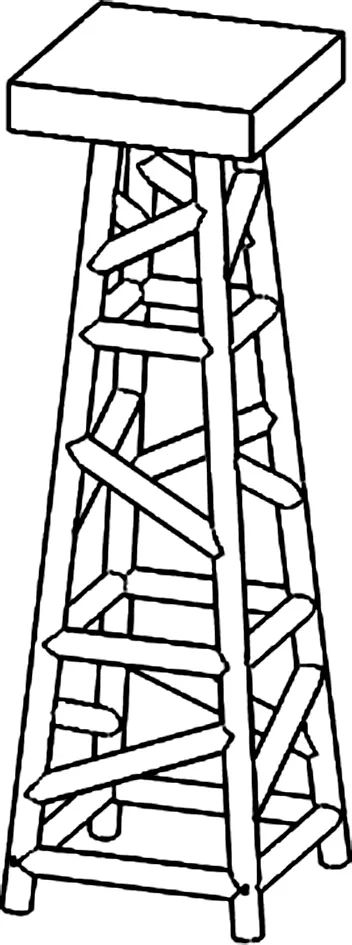
图8 结构拓扑优化设计的三维实体模型Fig.8 3D model for topology optimization design

2.5 响应曲面优化法确定杆件直径

响应曲面优化法是利用多元二次回归方程来拟合因素与响应值之间的函数关系,通过对回归方程的分析来寻求最优参数,解决多变量问题的一种统计方法．将承力面4根连杆和4根支撑柱的半径p1设置为2～3 mm,中间横杆和斜连杆的半径p2设置为1～2 mm,结构承受载荷F的变化范围设为20 000～100 000 N,杆件内的正压力不大于材料的压缩屈服强度,同时要保证结构的失稳因子大于1(结构不失稳),结构的总质量m要小于0.2 kg,利用ANSYS Workbench的响应面优化工具,对各杆径进行优化,得到的优化结果如表1．

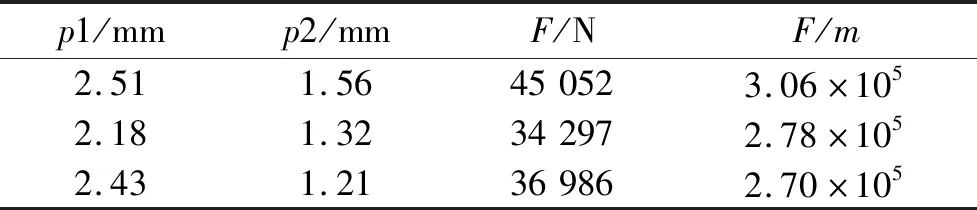
表1 杆件直径优化结果Table 1 Optimized results of rods

表1中看出,p1为2.51 mm,p2为1.56 mm时得到结构承载力F最大,且承载力与质量的比值(F/m)也最大．为选材方便,最终选用承力面4根连杆与4根支撑柱的半径为2.5 mm,中间横杆与斜连杆的半径为1.6 mm．

3 力学性能分析和试验

在ANSYS Workbench中导入最终优化结构的实体模型,其中支撑杆及顶部连接杆半径2.5 mm,其余部位连接杆半径1.6 mm,质量为0.156 4 kg．计算得到的静力变形如图9(a),失稳变形如图9(b),计算出临界失稳载荷为41 000 N,考虑到焊接会造成支撑杆产生一定变形,实际结构的临界失稳载荷小于计算值,预测为计算值的80%左右,约32 000 N．

图9 最终桁架结构及力学性能分析Fig.9 Final truss structure and mechanical properties analysis

基于设计的桁架结构进行焊接,选用ER70S-6焊条作为母材和焊材,采用手工TIG焊,焊接电流范围为70～80 A,焊接电压范围为10～12 V．为了减少焊接变形,自主设计了一套焊接夹具,如图10．将按设计尺寸加工好的杆件放入夹具凹槽中,按照先外框后内杆的顺序焊接,以减少焊接变形．焊接后结构照片如图11．将焊接好的结构在万能试验机上进行压缩试验,得到的最大压缩力为33 000 N,与预测的承载力非常接近,说明本文采用的设计方法所得结构的设计承载能力与根据设计结果焊接而成的桁架结构试验承载能力一致．

图10 焊接夹具Fig.10 Welding fixture

图11 焊接桁架照片Fig.11 Photo of welded truss

4 结论

(1) 逐级优化的设计思路,使设计的桁架在满足设计要求的情况下,保证承载力和质量配置的合理性．

(2) 综合采用有限元分析法,拓扑优化法和响应曲面优化法优化设计的结构的设计承载能力与根据设计结果焊接而成的桁架结构性能接近．

(3) 提出了利用比的设计变量,较好地解决了焊接桁架设计中的斜杆位置优化问题．