基于改进遗传算法对车间调度问题的研究∗
2020-05-15刘庆阁唐晓彬
曲 媛 刘庆阁 唐晓彬 魏 骁 王 硕
(中国船舶重工集团公司第七○三研究所 哈尔滨 150060)
1 引言
近年来,随着科技和行业要求逐步提升,车间调度问题逐渐成为现代制造企业关注的主要问题,同时也是生产制造领域研究的热点问题之一[1]。车间调度问题属于非确定性多项式难题,主要针对不同制造企业对生产车间、机器、人员、物流等调度不同,生产周期会随之变长的问题[2~4]。随着行业需求的不断上升,人工排产调度不仅会增强生产成本、延长生产周期,而且会浪费制造企业的部分生产资源[5~6]。同时车间调度问题是计算机集成制造系统工程中的一个重要组成部分,它对企业的生产管理和控制系统有着重要的影响。在当今的竞争环境下,如何利用计算机技术实现生产调度计划优化,快速调整资源配置,统筹安排生产进度,提高设备利用率已成为许多加工企业面临的重大课题[7~8]。
遗传算法是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法[9~11]。其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则[12~13]。遗传算法的这些性质,已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域,是现代有关智能计算中的关键技术[14]。
2 问题描述
有m个工作台(5<m<10),有n项作业(n>50),每项作业需要MTi时间(MTi为随机数)完成,每项作业均在工作台上完成,请采用优化方法实现这一优化作业方案。本文根据问题的复杂程度不同,给出以下约束条件:
1)每个工作台对应一道工序;
2)每个作业使用每个工作台不多于1次;
3)每个作业利用每个工作台的顺序可以不同;
4)No.2、3、4工作台上所对应的工序加工顺序必须满足先后顺序要求:2>3>4,后工序不能先于前工序,其他工序无顺序要求;
5)任何作业没有抢先加工的优先权,应服从生产顺序调度安排;
6)作业加工过程中没有新作业加入,也不能临时取消作业的加工。
根据以上定义和约束条件,要研究的问题是:确定各项作业在各个工作台的工作顺序,给出优化方案,优化生产,得到满足生产约束条件的较优生产时间。
3 建立模型及目标函数
车间调度问题的调度目的是确定各工作在不同工作台的工作顺序,得到满足约束条件的较优生产时间,建立车间调度问题的目标函数表示如下:
最小化完工时间f:
式(1)中i表示每个作业i∈{1,2,…,N},j表示每个工作台j∈{1,2,…,M},t_ij表示第i个工作在第j个工作台上的工作时间,H_j表示第j个工作台在开始生产后的未工作时间和,T_j表示第j个工作台耗时多少结束生产。式(1)表示第j个工作台的耗时等同于每个工作的工作时间和工作台未工作的空闲时间的总和。式(2)表示车间调度问题的目标函数即最小化M个工作台工作时长最大的工作台的耗时。
由于上述有约束条件:
1)每个工作台对应一道工序
2)每个作业使用每个工作台不多于1次
所以有:

式(3)中l代表每道工序l∈{1,2,…,M},由式(3)可知每个工作台对应一道工序,则一个作业需在每个工作台加工,且只加工一次。所以l=j且l,j∈{1,2,…,M},j工作台结束工作即所有工作的第j道工作已完成。M个工作台均结束任务后即所有工作的M道工序均已完成,生产结束。
3)No.2、3、4工作台上所对应的工序加工顺序必须满足先后顺序要求:2>3>4,后工序不能先于前工序,其他工序无顺序要求;
所以有:

式(4~5)中 Cij表示第i个工作在第j个机器上加工的开始时间即开始第j个工序的开始时间,式(4)表示,以刚开始生产的时间点为起始点,第i个工作在第2个机器上的开始时间加上第i个工作在第2个机器上的工作时间要小于第i个工作在第3个机器上的开始加工时间。同理,第i个工作在第3个机器上的开始时间加上第i个工作在第3个机器上的工作时间要小于第i个工作在第4个机器上的开始加工时间。
4 改进遗传算法
4.1 算法描述
本文提出了遗传退火算法解决生产过程中的车间调度问题,解决不同的约束条件下的调度问题。对车间调度问题进行编码,创建染色体和初始种群,进行选择、交叉、变异等一系列操作,得到目标函数值即为适应度函数值。之后进行选择,交叉,变异操作,再重复评价;在适应度值持续偏差不大后退出循环,输出适应度最大的解[15~16]。
流程图见图1所示。
4.2 编码与解码
编码:利用N个作业在M个工作台工作构建染色体,一个染色体上基因数量为N×M,是由M个N基因组成。例如:N=3,M=2,则染色体可以为[1,2,3,1,2,3]。

图1 改进遗传算法流程图
解码:假设此次车间调度问题为N=3,M=2,3个工作的工作编号为1-3,将1-3每个编号均随机生成2次作为一条染色体记作数组b[6]。假设j=b[i],i代表要安排的第几个任务i∈{1,2,…,N×M},j代表第i个安排的任务为第j个工作,b[6]=[1,3,3,2,2,1],从左至右依次判断安排工作,b[1]=1则表示第一个要安排的工作为第1个工作,b[2]=3则表示第二个安排的工作为第3个工作。同理安排到b[5]时,b[1]到 b[4]中 i的数量为工作i已完成的工序数目。
4.3 初始化种群
首先随机生成L条含N×M个基因的染色体构成初始种群,每条染色体代表一个个体,即车间分配任务的一种可行调度。
4.4 适应度计算
根据编码方式得到j=b[i]判断可进行当前j工作的工作台;再从中判断可用工作台的运行进程,即之前工作运行结束的结束时间,将当前工作赋给结束时间最小的工作台;重复上述操作将所有工作安排完成后,记录各台机器最终的结束时间,并找出其中结束时间最大的工作台,将其结束时间进行变换后作为适应度值进行评价。假设有N=60个工作,M=8个工作台,具体步骤如下:
1)建立e[i][j]数组存储工作台在当前工作完成后各工作台的工作进程;
2)从b[1]到b[480]顺序判断应放到哪个工作台上,当j=b[i]]判断可进行当前j工作的工作台;
3)当 l=1,2,5,6,7,8时 e[l][j]为空,即此时 j工作未完成的工序 l,或 l=3时 e[2][j]不为空,即j工作的2工序已完成,当前可加工3工序,或l=4时e[3][j]>e[2][j],即 j工作的 3 工序已完成,当前可加工4工序;
4)将当前可加工的工序数存入c[]数组中,c[ii]数组存储可进行当前工作的工作台;
5)再计算当前可进行j工作的工作台的运行进度,将当前工作赋给进度最小的工作台l,并将该工作j的需工作时间a[j]加上上一时刻l工作台的结束时间的记入e[l][j]数组即为此时l工作台的运行结束时间;
6)num变量存储当前工作j已完成的工作台数量,记入f[l][h]数组(即j工作的完成工序顺序)用于输出;
7)编写函数Comparetime(),用于将各工作台的最终结束时间赋给g[ii]数组;
8)编写函数evaluation(),用于评价遗传算法,将种群中的染色体按适应度进行排序。
4.5 选择操作
在遗传算法中,通常从一个父代种群中选择一部分遗传给子代,为避免损失有效基因,所以提高适应度较大的个体被选择的概率,从而提高算法的收敛效率,降低计算时长。本文采用传统的轮盘赌的方式来选择子代染色体,编写函数selection(),用于选择个体。
4.6 交叉操作
在遗传算法中,交叉操作是为了在不发生优质基因损失的情况下产生新的个体,本文中通过交叉两个父代个体产生两个新的子代个体,由于编码方式染色体b[i]中必须含有M个N工作,假设有N=60个工作,M=8个工作台,即b[i]是由8个1~60的编号组成,任意交叉会破坏染色体结构,使染色体失效,所以本文编写了函数cross(),用于进行遗传算法中的交叉操作,交叉操作找出相同的数据段按照原有的顺序进行两段基因的交换到不同的染色体上。
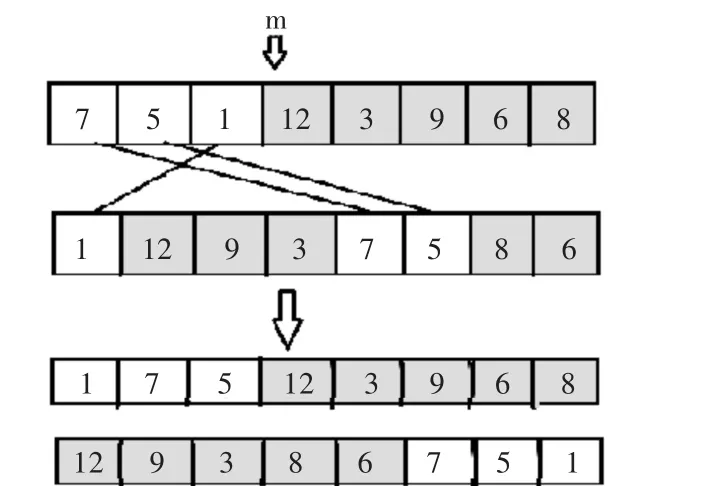
图2 改进遗传算法的交叉操作实例
具体步骤如下:
1)见图2,在1~480中选择一个随机数m,将父代1中m-480的基因取出记作ff[]数组,将父代1中1-m的基因记作father1[]数组;
2)分别计算ff[]数组中各个工作i的数量;3)在父代2中从左至右抽出相应基因并以父代2的编码排列形式排列记作ff1数组;
4)将父代2中剩余基因,以本身排序方式排序记作father2[]数组;
5)将father1[]数组同ff[]数组合并,同时将fa⁃ther2[]数组同ff1[]数组合并。
4.7 变异操作
编写函数mutation(),用于进行遗传算法中的变异操作。将父代中一个染色体的两段基因互换位置形成一个新的子代个体。
输出结果:
1)编写函数record(),用于记录最优解和判断是否满足条件;
2)编写函数showresult(),用于输出最终结果
3)程序主函数如下,添加计时函数clock计算程序运行时间,并输出最终各工作台用时、最长耗时的工作台用时、最短耗时的工作台用时、两者差值、各工作台进行工作的编号和算法运行时间。
5 车间调度问题的实例仿真
调度实例分析,假设M为8,N为60,每个工作对应的时间如表1所示。
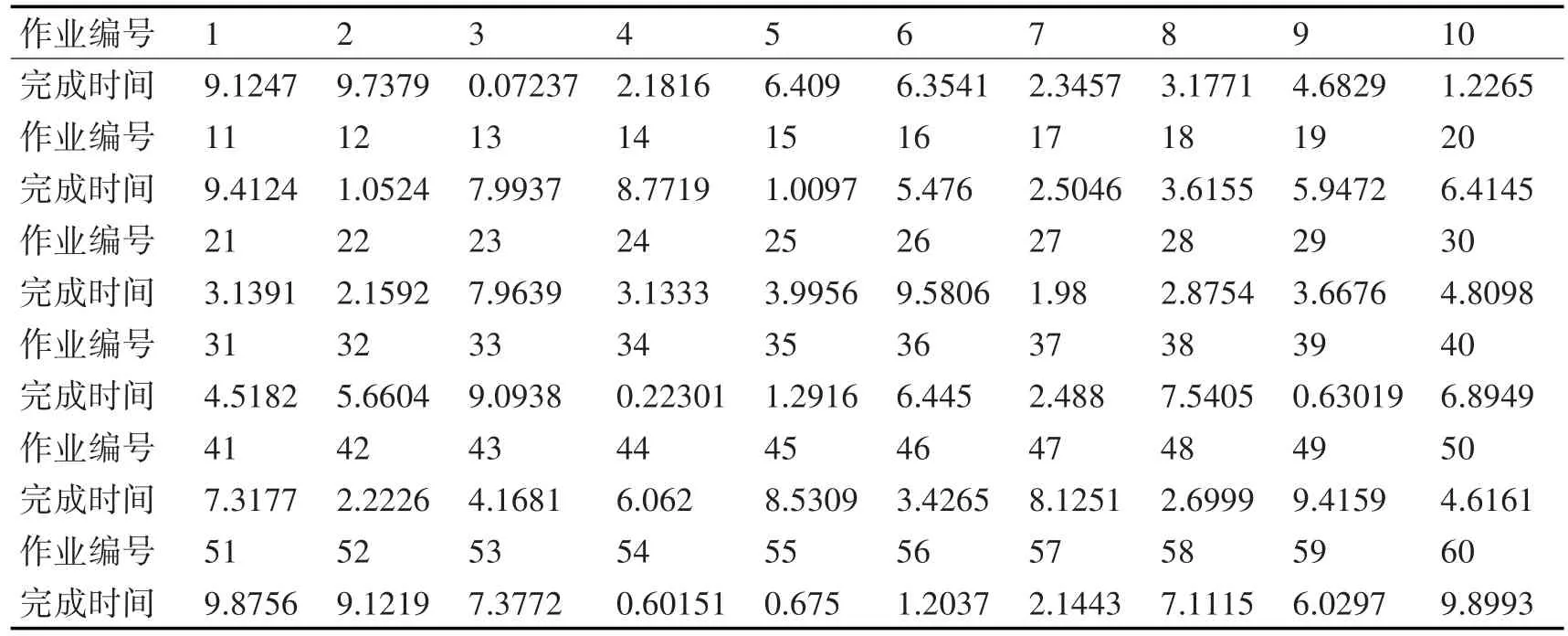
表1 各个工作对应的工作时间
设定种群数量SUM为4000,交叉概率为0.7,变异概率为0.09,应用模拟退火算法在10条染色体的适应度值相差不超过0.001时结束算法。得到的一组最优解见表2。
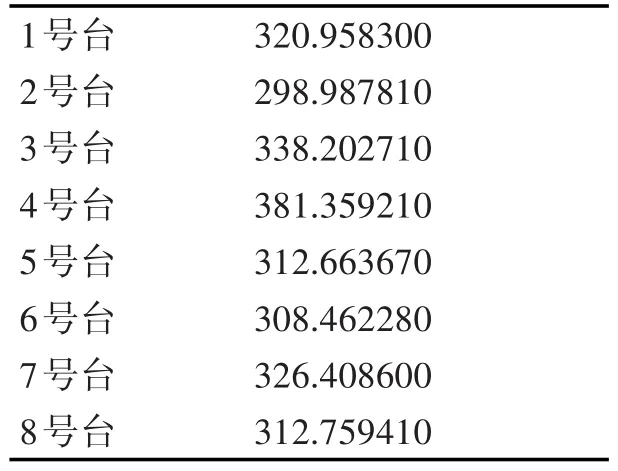
表2 仿真最优解:每个工作台的工作总时间
其甘特图见图3。

图3 仿真最优解对应甘特图
其中灰色代表工作时间,白色代表未工作时间。
最优解工序表如图4。
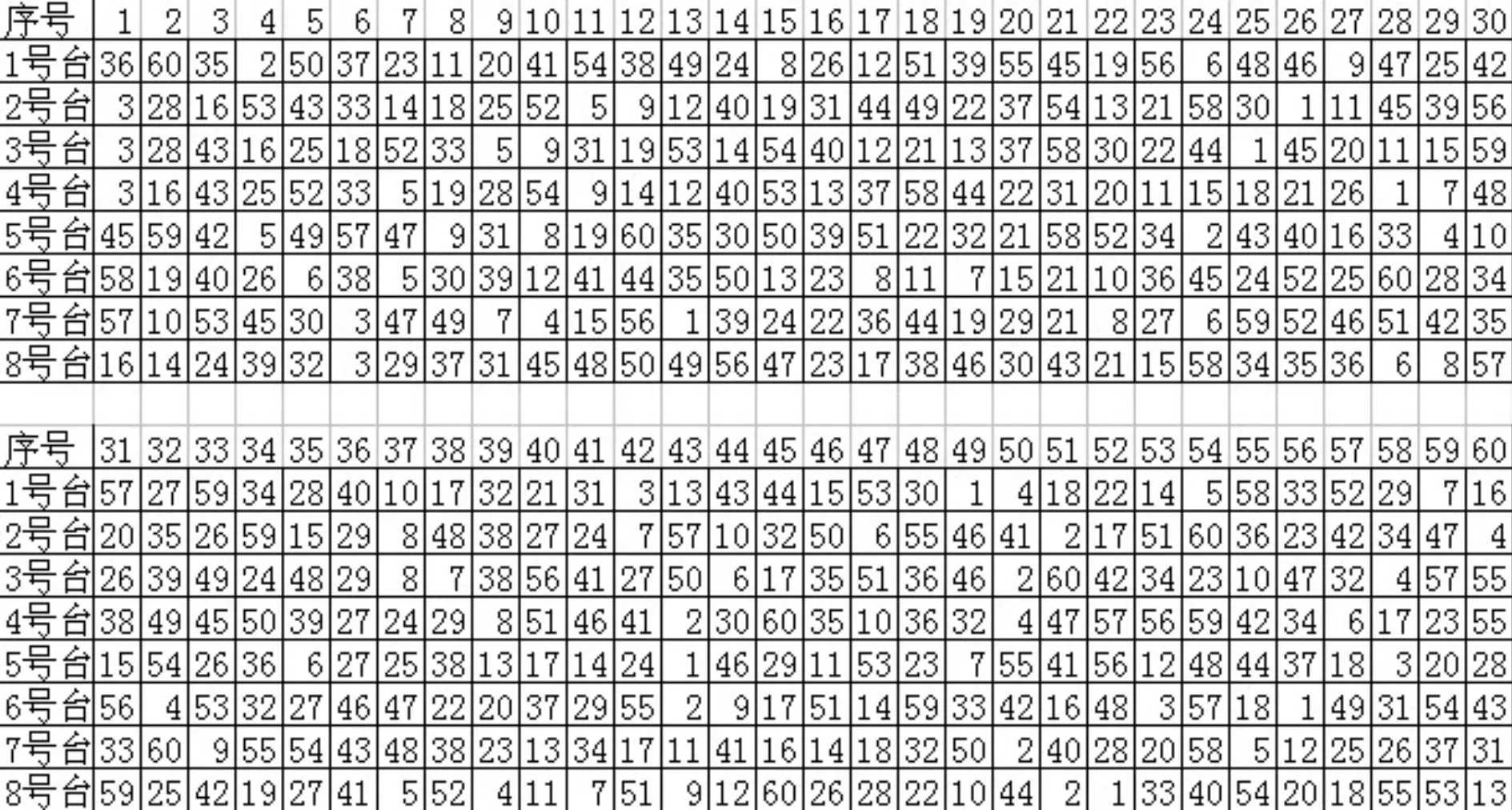
图4 各个工作台工作各个作业的顺序图
总工作时间为2369.7952h,平均每台位工作296.2244h,该算法所得结果较均值略有差异,结果较为满意。
将算法运行100次,记录每次优化结果和耗时,算法结果如图5。
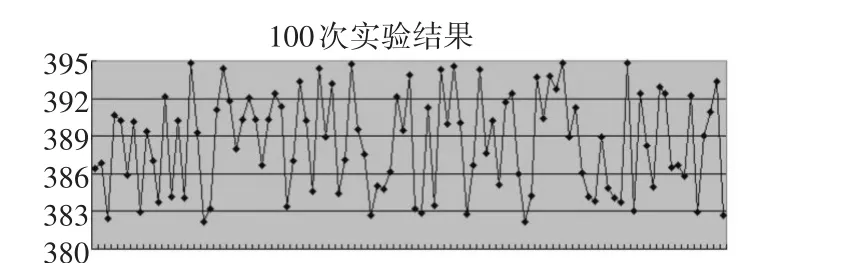
图5 100次运行算法的最优解曲线图
平均耗时387.08709h,从曲线上可看出算法较为稳定。每次算法平均耗时141.221s。
6 结语
本文对改进遗传算法解决车间调度问题展开了深入的研究。车间调度问题是NP型问题,通过改进的遗传算法可有效解决车间调度问题,得到满足生产约束条件的较优调度,有指导生产,大幅减少生产时间的功效。同时通过仿真实验有效证明了本算法的全局搜索能力较好,能得到较优的实验结果,且算法较为稳定。
