基于稀疏回归和谱分析的无监督特征选择算法∗

周婉莹 马盈仓

（西安工程大学理学院 西安 710048）

1 引言

由于存在大量高维数据，特征选择作为许多任务的预处理步骤占据关键位置，如聚类［1～2］，分类［3～4］，人脸识别［5～6］等。关于是否使用标签，特征选择分为三类：监督、半监督和无监督。由于获取数据标签十分费力，因此无监督特征选择在现实中更实用，更富有挑战。

无监督特征选择方法主要包括过滤式方法［7～9］，包装式方法［10］，嵌入式方法［11～15］。其中，嵌入式方法最常用，文献［16］概述结构化稀疏特征选择，这是一种嵌入式方法。嵌入式方法将特征选择和训练模型结合，模型优化期间直接评估特征重要性。为利用数据几何结构，现有的无监督特征选择大多采用谱分析方法，大量文献证实该方法具有良好性能［17］。

传统基于谱分析的特征选择方法［18～19］包括两个步骤。首先，通过图拉普拉斯算子或非负矩阵分解探索数据结构。然后，利用稀疏正则化学习特征权重矩阵进行特征选择。这些方法至少存在两个问题：1）独立构造相似矩阵和选择特征，导致相似矩阵只能从原始数据导出，在后续过程中保持不变；2）仅侧重选择在聚类或分类任务中起决定作用的判别特征，忽略了特征冗余。如人脸图像中有眼睛、鼻子、嘴巴等特征，选择冗余高的特征会使数据失去多样性且降低其在聚类或分类任务中的性能。因此，我们考虑建立基于谱分析和稀疏回归的无监督特征选择算法。

2 模型建立

其中，F={ f1，f2，…，fn} ∈ℜn×m是数据的指示矩阵，fi是低维流形中第i个样本的指示向量。通过对特征权重矩阵W施加正交约束WTW=I，使模型在优化过程中保持数据结构，避免奇异解。同时对F施加正交约束FTF=I，来减少维数和避免奇异解。

模型（1）利用最小二乘回归探索数据低维结构，未能发现局部几何结构。谱分析表明，数据的局部几何结构可通过最近邻有效建模。考虑模型（1）中指示矩阵F也是低维空间中的数据结构。自然想到，如果两个数据点xi和xj邻近，它们的指示向量 fi和 fj也应该邻近。基于此，构造图正则项，表示为用谱分析中一个基本但重要的等式：将模型（1）优化为

S第i个对角元素为

为了自适应的构造相似矩阵S，定义样本点xi可被所有其他样本连接的概率为sij( j =1，2，…，n )，sij是相似矩阵S的元素。两数据相邻的概率可视为它们的相似性。根据常识，较近的样本具有较大的连接概率，因此sij与xi和xj之间的距离成反比。采用欧氏距离的平方，即确定概率s的方法是解决下面问题：

其中sij是向量si∈ℜn×1的第 j个元素。为避免S某些行全部为零，为S添加约束siT1=1，使S行和为1。问题（4）只有最近数据点可以使xi邻域的概率为1，且其他数据点不是xi的邻域。所以在不涉及数据点任何距离信息的情况下，解决下面问题：

该问题的最优解使所有数据点都可以是xi的邻域，且具有相同概率结合问题（4）和问题（5），解决下面问题：

其中第二项是正则项，γ是正则化参数。根据流形学习理论，总会存在一个低维流形可以表达高维数据的结构。参考文献［20］，使用线性组合XW将原始特征映射到低维流形中。应用到问题（6），得到

通过以上分析，将问题（7）与模型（3）结合，给出无监督特征选择的优化目标如下：

其中β是参数。为保证更好的结果，使用W 的ℓ2，1范数对W正则化，确保用于选择特征的W行稀疏，减少特征冗余。得到自适应的基于稀疏回归和谱分析的无监督特征选择（SSUF）的模型如下：

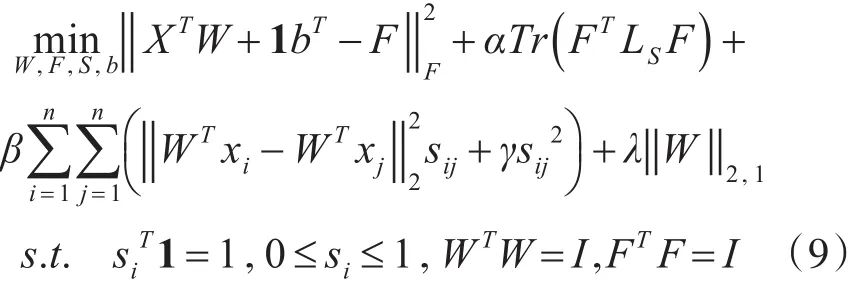
其中λ是正则化参数，可确定W的稀疏程度，λ越大，W越稀疏，‖‖W2，1越小。W的ℓ2，1范数定表示向量wi的ℓ2范数，‖‖wi2越大，表示第i个特征越重要。

已经全面介绍了SSUF模型，如何解模型（9）成为当务之急。

3 模型求解

模型（9）的优化涉及四个变量：W ，F，S和b。显然，b不受任何约束。根据KKT定理［21］，变量b可通过模型（9）的拉格朗日函数的一阶导数确定。模型（9）关于b的拉格朗日函数为

模型（10）仅涉及三个变量：W ，F和S。下面采用交替迭代优化方法，即交替固定两个变量优化另一个变量。

3.1 固定W和F，更新S

当W 和F固定时，模型（10）转化为

根据等式（2），得到

下面，推导问题（12）的封闭解。拉格朗日函数为

其中，θ和φi≥0是拉格朗日乘子。等式（13）关于si求导并令其等于0：

事实上，关注数据局部结构可获得更好的性能。因此，我们学习一个稀疏的si，即只有xi的k个最近邻才能连接到xi。学习稀疏相似矩阵S的另一个好处是可以大大减轻实验的计算负担。

假设di1≤di2≤…≤din。如果最优的si只有k个非零元素，根据等式（15），知道 sik＞0且si，k+1=0 。因此，有

由等式（15）和约束条件siT1=1，可以得到

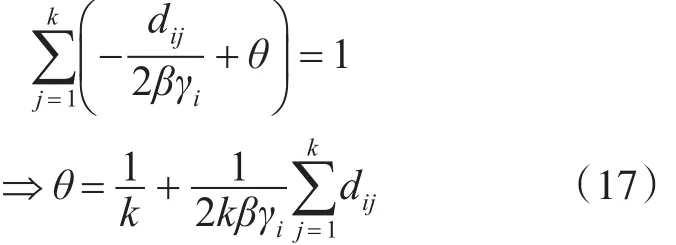
因此，根据问题（16）和（17），得到关于 γi的不等式：

为了获得恰好具有k个非零元素的si的最优解，将γ设置为

因为k是一个整数且具有明确含义，所以邻域数k比正则化参数γ容易确定。

3.2 固定W和S，更新F

固定模型（10）W 和S，优化F等于求解：

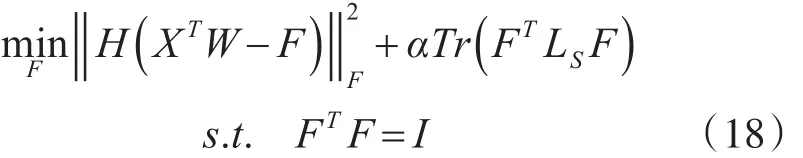
根据矩阵性质，模型（18）满足下面推导：

由于W 固定，经上述推导，模型（18）等价于求解：

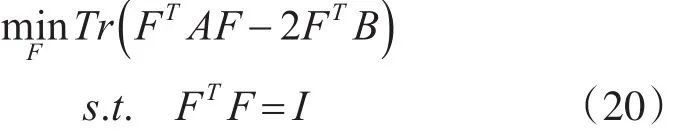
其中，A=H+αLS，B=HXTW 。

因为问题（20）与Stiefel流形二次问题标准形式一致，它可通过文献［22］提出的广义幂迭代算法有效解决。算法1给出详细过程。

算法1：解决问题（20）

输入：矩阵 A∈ℜn×n和 B∈ℜn×m

初始化：随机矩阵 F∈ℜn×m满足 FTF=I，正定矩阵A͂=υI-A∈ℜn×m，υ为任意常数

Repeat：

1）更新 M ← 2A͂F+2B

2）通过M 的紧致奇异值分解计算USVT=M，其中U∈ℜn×m，S∈ℜm×m，V∈ℜm×m

3）更新 F←UVT

Until收敛

输出：指示矩阵F∈ℜn×m

3.3 固定F和S，更新W

当F和S固定时，模型（10）变为

其中，S是相似矩阵。

又根据文献［24］，当 wi≠0( )i=1，2，…，d ，关于W的导数为

问题（23）同样用广义幂迭代方法求解，详细算法在算法2给出。算法3总结了SSUF算法。

算法2：解决问题（23）

输入：矩阵C∈ℜd×d和 E∈ℜd×m

初始化：随机矩阵W∈ℜd×m满足WTW=I，正定矩阵C͂=υI-C∈ℜd×d，υ为任意常数

Repeat：

1）更新 N←2C͂W+2E

2）通过 N的紧致奇异值分解计算USVT=N，其中U∈ℜd×m，S∈ℜm×m，V∈ℜm×m

3）更新W←UVT

Until收敛

输出：特征权重矩阵W∈ℜd×m

算法3：SSUF

输入：数据矩阵 X∈ℜd×n，中心矩阵 H∈ℜn×n，参数α，β，λ和k

初始化：相似矩阵 S∈ℜn×n，随机矩阵 F∈ℜn×m满足FTF=I，随机矩阵W∈ℜd×m满足WTW=I

Repeat：

1）通过等式（15）更新 S

3）通过算法1更新F

4）通过算法2更新W

Until收敛

输出：将 ‖wi‖2(i=1，2，…，d )按降序排列，选出前 l个特征作为特征子集I

4 收敛性分析

本节将证明算法SSUF收敛。令

由不等式（26）可知，不等式（24）成立，算法SSUF收敛。

5 实验

本节进行特征选择实验，验证SSUF算法的有效性和优越性，在展示实验结果之前，先详细介绍一些实验方案。

5.1 数据集

提出的SSUF算法在四个真实数据集上进行评估，包括两个面部图像数据集，UMIST［13］和 ORL［11］；一个物体图像数据集，COIL20［25］；一个生物数据集，LUNG［26］。表1总结了这些数据集的细节。

5.2 实验设置

1）对比算法

为验证SSUF的有效性，将其与五种常用的无监督特征选择方法比较，包括拉普拉斯评分法［7］（LS）、多聚类特征选择［11］（MCFS）、无监督判别特征选择［27］（UDFS）、鲁棒无监督特征选择［9］（RUFS）、鲁棒图正则化无监督特征选择［20］（SOGFS）。下面详细描述这些方法。

LS：通过构建样本拉普拉斯近邻图，以特征局部保持能力为准则对样本特征权重排序，采用启发式策略逐个选取最优特征构成特征子集。

MCFS：通过谱分析捕获局部流形结构，对特征权重施加ℓ1范数正则化使特征稀疏，选择最能保持聚类结构的特征，提高特征局部保持能力。

UDFS：采用局部类间散度最大化与类内散度最小化策略获取最优特征子集，将判别分析和ℓ2，1范数结合到无监督特征选择中。

RUFS：使用灵活流形嵌入、非负矩阵分解和ℓ2，1范数同时执行聚类和特征选择。

SOGFS：自适应确定相似矩阵，同时进行局部结构学习和特征选择。

2）参数设置

在相同策略中设置所有方法的参数使实验公平，即搜索网格 {10-4，10-3，10-2，10-1，1，101，102，103，104}，并记录最优结果。为消除K-means聚类方法引起的随机效应，执行20次随机起点的K-means，且最终报告平均值。所选的特征数量在{50，100，150，200，250，300} 中变化。还使用所有特征执行K-means作为基线。

3）评价指标

使用两种广泛使用的评价指标评估所选特征的性能，精确度（ACC）和归一化互信息（NMI）。ACC和NMI的值越大，代表特征选择的效果越好。

5.3 实验结果与分析

使用不同数量所选特征的ACC和NMI评估每种方法的性能。图1和图2清晰展示了几种不同特征选择算法在四个数据集上的效果。图中横坐标表示选择特征的个数，纵坐标分别表示以ACC和NMI作评价指标时的值。从图中可明显看出，本文提出的SSUF算法在大多数实验中优于其他5种方法，甚至优于Baseline。

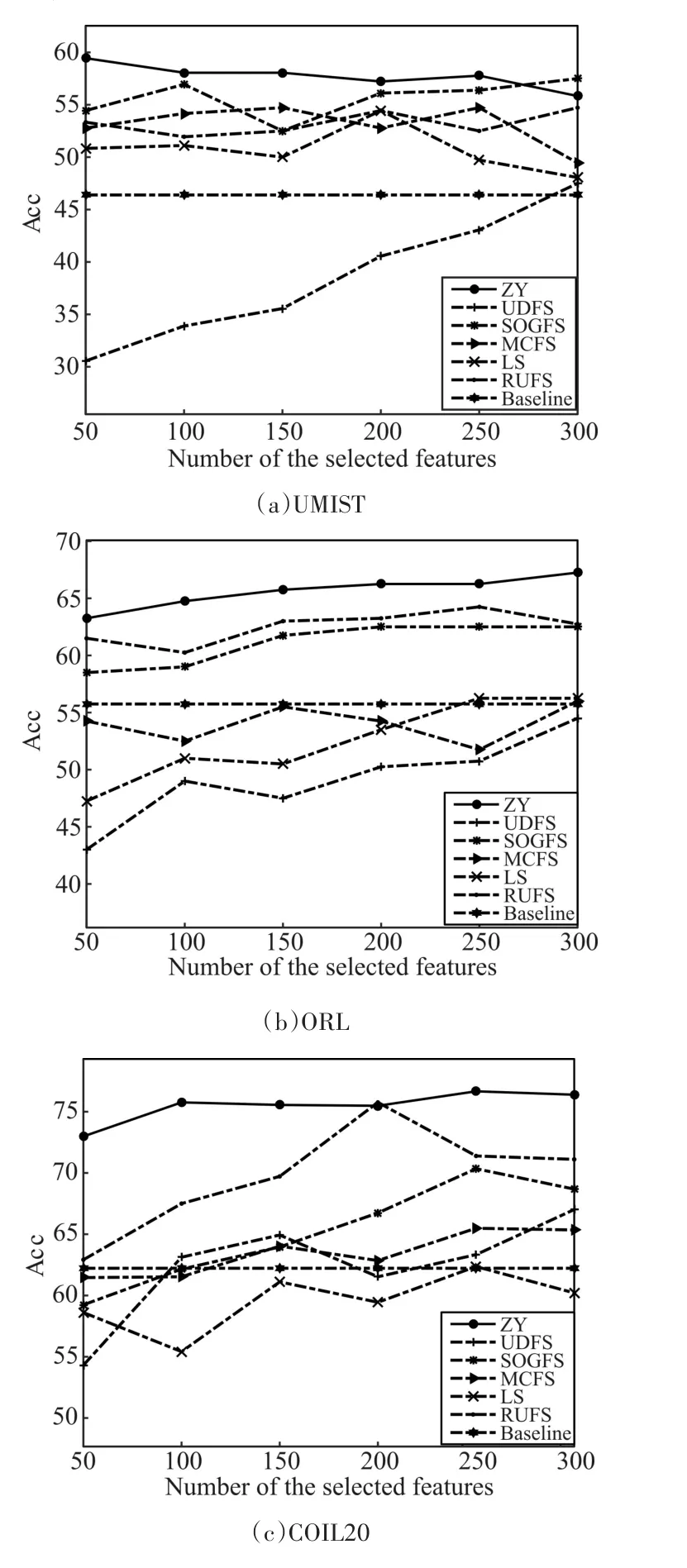
具体来说，以ACC作评价指标时，在UMIST数据集上，选择特征数50，100，150，200，250时，都是最佳结果，且与次佳结果相比，有大约3%改进；在ORL数据集上，与次优方法RUFS相比，有3%改进；在COIL20数据集上，选择特征数50，100，150，250，300时，达到最佳效果，与次佳结果相比，有大约8%改进；在LUNG数据集上，选择特征数100，150，200，250，300时，都是最佳结果，与次佳结果相比，有大约4%改进。以NMI作评价指标时，在UMIST数据集上，选择特征数50，100，150，200时，达到最佳结果；在ORL数据集上，与次优方法RUFS相比，有2%改进；在COIL20数据集上，与次佳结果相比，有大约3%改进；在LUNG数据集上，选择特征数100，150，200，250，300时，达到最佳结果，与次佳结果相比，有大约7%改进。

图2 选择不同特征数的4个数据集归一化互信息

通过特征选择，获得更有价值的精确数据。与使用所有特征执行K-means的基线Baseline相比，使用SSUF算法进行特征选择的结果更好。这直接说明特征选择可以提高数据质量。

5.4 参数灵敏度

为研究SSUF的参数灵敏度，使用ACC评估参数α，β和λ。通过两个数据集ORL和COIL20展示结果。图3中，（a）和（b）分别表示在数据集ORL和COIL20上选择不同特征数时，固定 β=10和λ=0.0001，随参数 α 变化ACC的变化情况；（c）和（d）分别表示在数据集ORL和COIL20上选择不同特征数时，固定α=10和λ=0.0001，随参数 β变化ACC的变化情况；（e）和（f）分别表示在数据集ORL和COIL20上选择不同特征数时，固定α=10和β=0.0001，随参数λ变化ACC的变化情况。可以看出，SSUF对α和 β不敏感，对 λ敏感。作为‖‖W2，1正则项的系数，λ影响W的稀疏性。当λ较大时，得到的W有更多的行是稀疏的，在某种程度上可获得更精确的特征序列。

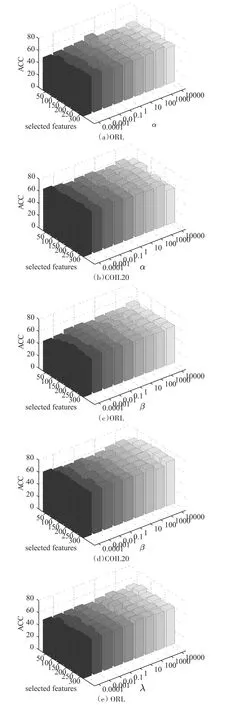
图3 算法的参数灵敏度

6 结语

本文利用最小二乘回归模型结合谱分析和稀疏正则化提出一个无监督特征选择算法。该算法能够选择更稀疏的特征，使特征之间相互竞争，消除冗余。此外，还设计了交替迭代算法解决提出的SSUF，并且在4个真实数据集上与几种常用方法的对比实验证实了SSUF的有效性和优越性。我们未来的工作之一是用ℓ2，0范数‖‖W2，0替换稀疏正则项‖‖W2，1，研究对特征选择的影响。