基于改进的小波相关性信号降噪算法∗

王益艳

（1.四川文理学院智能制造学院 达州 635000）（2.达州智能制造产业技术研究院 达州 635000）

1 引言

在实际的计算机控制系统中，采样信号不可避免地受到各种噪声的和干扰的污染，使得由辨识采样信号得到的系统模型存在偏差，而妨碍了系统控制精度的提高［1］。如何从这些受噪声干扰的信号中估计得到“纯净”的信号，是建立系统高精度模型和实现高性能控制的关键。另一方面，在实际的工程应用中，大多数信号可能包含着许多尖峰或突变，而且噪声信号也并不是平稳的白噪声［2］。对这种信号进行降噪处理时，传统的傅里叶变换完全是在频域中对信号进行分析，它不能给出信号在某个时间点上的变化情况，因此分辨不出信号在时间轴上的任何一个突变。因此，对于非平稳信号，在低信噪比的情况下，经过FFT滤波处理，不但信噪比得不到较大改善，而且信号的有效信息容易被模糊掉［3］。

近年来，小波理论得到了迅速发展，由于小波具有低熵性、多分辨特性、去相关性和选基灵活性等特点［4］，所以它在处理非平稳信号、去除信号噪声等方面表现出强有力的优越性。小波阈值降噪方法认为对于小波系数包含有信号的重要信息，其幅值较大，但数目较少，而噪声对应的小波系数是一致分布的，个数较多，但幅值小。Donoho提出的基于软硬阈值处理思想的小波域降噪技术［5～6］，它对信号先求小波系数，再对小波系数进行阈值处理，最后通过小波反变换得到重建后的信号。但因为其尺度是按二进制变化的，因此，在高频段其频率分辨率较差，而在低频段其时间分辨率较差［7～8］。后来人们提出了很多新的改进方法，如模极大值滤波方法，小波包分析方法等［9～11］，在一定程度上提高了降噪效果，为了充分利用小波系数直接的相关性，人们提出了相关性降噪算法［12～14］，但传统相关性降噪方法容易依赖小波系数，而小波系数无平移不变性，容易出现偏移导致引起误判［15］。基于此，本文在相关降噪算法的基础上，提出了一种改进的区域相关降噪算法。该方法对一个区域内的小波系数进行相关性度量，克服了传统方法的不足。最后，通过对两组非平稳信号降噪进行对比实验，结果表明，该方法对比传统小波方法具有更好的降噪效果，主观视觉效果更好，信噪比SNR、均方根误差RMSE等性能指标更好。

2 相关性降噪方法及其改进

设噪声模型为［4］

式中，x(n)为原始信号，f(n)为受噪声干扰的信号，s(n)为高斯白噪声，它服从分布。利用小波变换得：

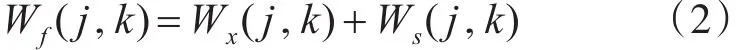
其中，Wf、Wx、Ws分别为 f、x、s对应的小波变换系数。小波变换降噪的目的就是从有噪信号的小波系数Wf中得到原始信号的小波系数Wx的估计Ŵx。

由于信号小波系数的上下层之间具有强相关性，而噪声没有这种相关性。相关性降噪方法就是基于这种相关性的。下面分别给出相关性系数和归一化相关性系数的定义。

定义1：相邻尺度同一空间位置小波系数的相关量定义为

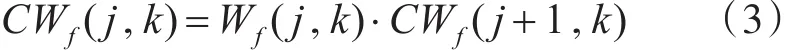
其中，CWf(j，k)称为尺度 j上点k处的相关性系数。

尺度空间上的相关性使噪声的影响大大减小，可以有效增强信号的细节，并且在小尺度上的作用明显大于在大尺度上的作用。而噪声能量主要是分布在小尺度上的，因此，这种随尺度增大而作用强度减小的性质，恰好对尽可能减小有效信息损失极为有利。

为了是相关性系数与小波系数具有可比性，进一步定义归一化相关性系数如下：

定义2：设

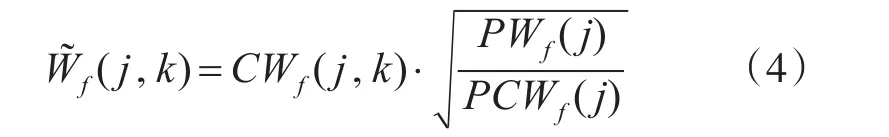
称W͂f(j，k)为归一化相关性系数。其中，PWf(j)表示第 j层系数的能量，PCWf(j)表示第 j尺度的相关性系数能量。即

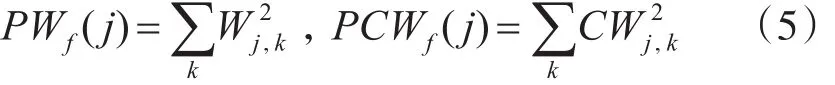
归一化相关性系数W͂f(j，k)与小波系数Wf(j，k)具有相同的能量［10］。相关性降噪的原理是比较每一层每一个位置的归一化相关性系数，从相关性的大小判断是信号还是噪声控制的点。具体实现过程如下：

1）给定分解层数N，选取合适的小波函数，计算加噪信号 f(n)每一层的小波系数Wf(j，k)。

2）根据式（3）～（5）计算归一化相关性系数W͂f(j，k) 。 比 较 W͂f(j，k) 和 Wf(j，k) ，若W͂f(j，k)≥ Wf(j，k)，则认为大相关量对应信号的特征 ，取 W͂f(j，k)=Wf(j，k) ，置 Wf(j，k)=0 。 若W͂f(j，k)＜Wf(j，k)，则认为点 k 处的小波系数由噪声控制，保留Wf(j，k)，置W͂f(j，k)=0 。

3）在每一个尺度上重新计算W͂f(j，k)。

4）重复2）～3）的过程。

5）所取W͂f(j，k)中各对应由信号控制的点，而Wf(j，k)中全部为噪声对应的点。

上述相关性降噪方法对小波系数的计算依赖性很强，一旦在小波分解的过程中，计算结果出现一定偏差，则由式（3）计算出来的相关性系数Wf(j，k)不能很好的刻画k点处的真实相关性，导致在上述算法中相关性系数与小波系数失去可比性。

改进的办法是采用区域相关性降噪，通过引入区域相关的概念，即考虑了点k处系数及其周围的系数，改进CWf(j，k)的计算方法。从而有效削弱了传统方法因小波系数平移所带来的不良影响。

定义 3：设 CNf(j，k)=Nf(j，k)⋅Nf(j+1，k)，则称CNf(j，k)为尺度 j上k点处的区域相关性系

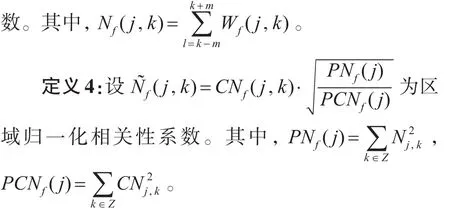
改进的区域相关性降噪方法与传统方法实现过程类似，只要用 CNf(j，k)和 N͂f(j，k)分别替代CWf(j，k)和W͂f(j，k)即可。

3 实验结果与分析

为验证本文方法的有效性，采用信噪比（SNR）、均方根误差（RMSE）进行客观评价。SNR和RMSE的表达式分别为

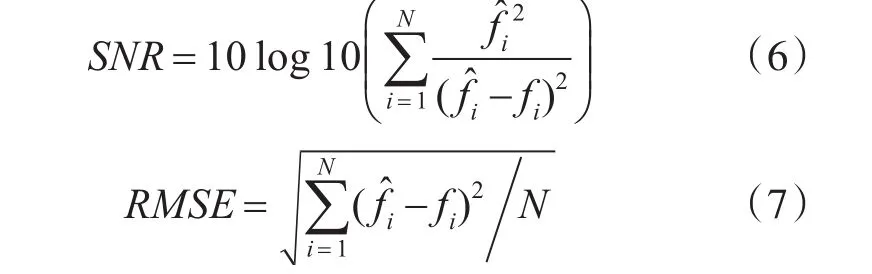
式中，f表示原始信号，f̂表示恢复信号。N表示信号的长度。SNR值越大，RMSE值越小，信号降噪效果越好。

本文进行了两组实验，分别采用电网电压采样信号和医学心电信号ECG作为测试对象，如图1所示。

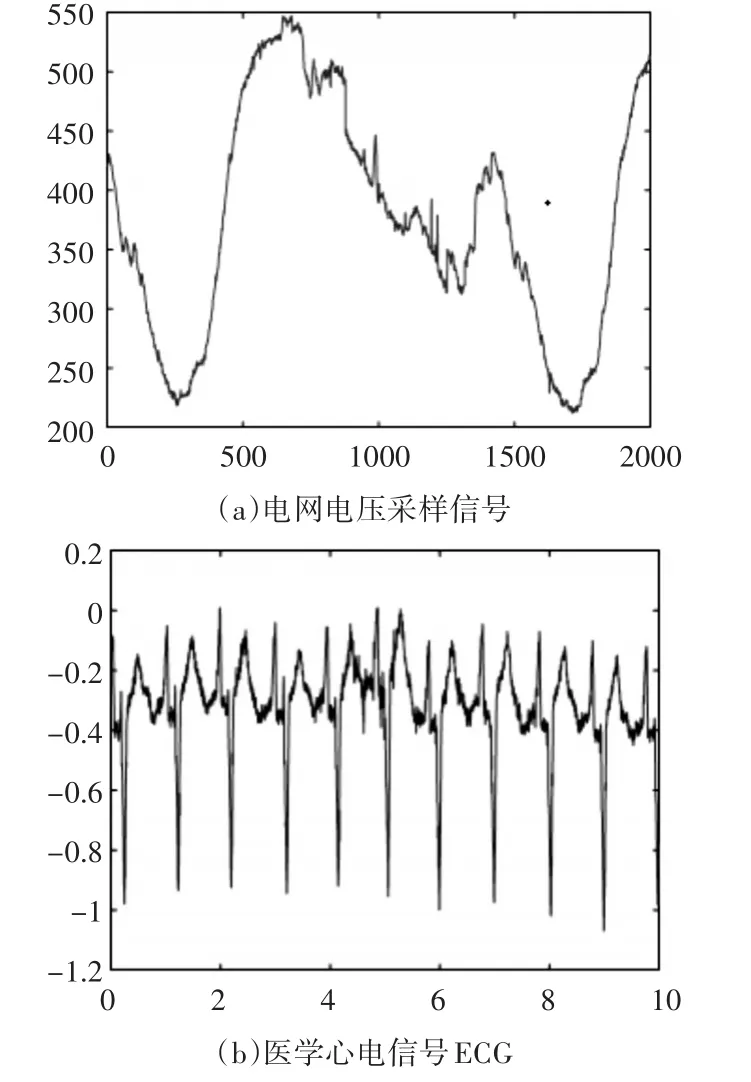
图1 实验测试对象

以Matlab R2015a为测试平台，计算机配置为：Windows7系统、AMD A8处理器、主频1.60GHz、4G内存。将本文方法与小波变换［11］、小波包变换［9］等方法进行对比实验，其中小波基均为”db3”，分解层数为4层。恢复信号的主观视觉效果如图2和图3所示，各降噪方法对应的性能指标比较如表1所示。

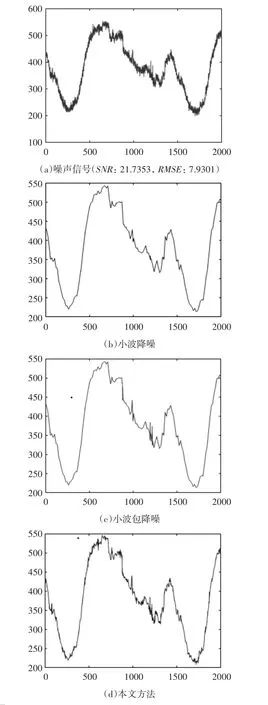
图2 各种方法对电网电压采样信号降噪对比实验结果

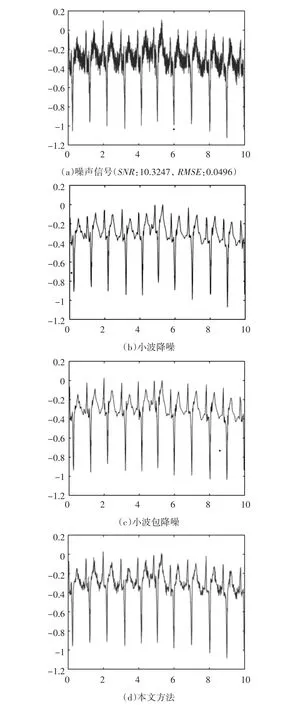
图3 各种方法对医学心电信号ECG降噪对比实验结果

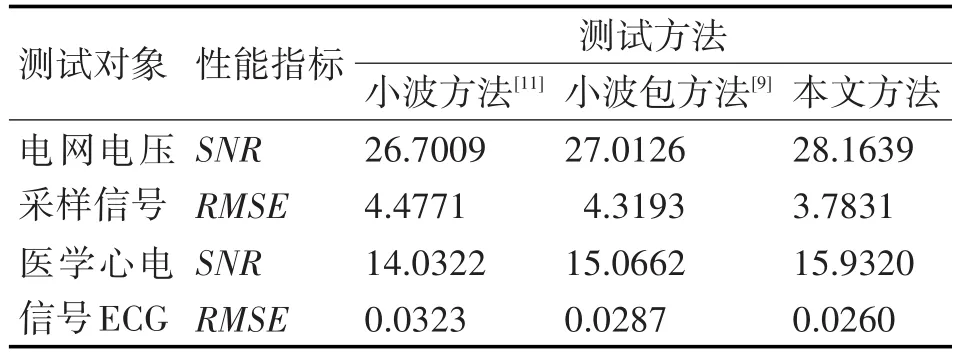
表1 各降噪方法对应的性能指标比较

由图2和图3可看出，本文方法降噪效果明显优于小波方法和小波包方法，对边缘、拐点等细节保持更好，与原始信号更逼近。从表1中性能指标来看，两组测试实验中，本文方法对应的SNR值都是最高，RMSE值都是最低，从侧面也表明了本文方法的优越性。

4 结语

针对非平稳信号降噪问题，本文在相关降噪算法的基础上，提出了一种基于区域信息的改进算法。该方法对一个区域内的小波系数进行相关性度量，有效削弱了传统方法因小波系数平移所带来的不良影响。

通过对电网电压采样信号和医学心电信号ECG的仿真对比实验，结果表明，该方法对比传统小波方法具有更好的降噪视觉效果，各项客观性能指标更优，体现了本文方法的有效性，