融合用户对项目子信息兴趣变化的协同过滤算法∗
2020-05-15廖闻剑
高 宇 廖闻剑
(1.武汉邮电科学研究院 武汉 430074)(2.南京烽火软件科技有限公司 南京 210019)
1 引言
21世纪以来,互联网给人们带来了极大的便利,同时也产生了大量的信息,使得人们获得又用的信息变得愈加困难,导致了所谓的信息过载(In⁃formation Overload)问题。搜索引擎在很大程度上缓解了这个问题,但是其提供的共性信息并不能满足不同用户的不同偏好。推荐系统的产生,旨在学习用户的历史行为数据,获取到用户的偏好,为用户产生个性化推荐。推荐系统算法主要有基于领域的算法,其中有基于用户的协同过滤算法(User⁃CF)、基于物品(itemCF)的协同过滤算法、隐语义模型(LFM)及基于图的模型协同过滤算法[1~2]。基于用户(UserCF)的协同过滤算法是推荐系统中最古老的算法,可以说这个算法标志着推荐系统的诞生,一直以来都是推荐系统领域最著名的算法。在协同过滤算法中,确定目标用户的近邻是整个算法的核心。传统的利用用户评分矩阵计算相似度的方法有余弦相似度、改进的余弦相似度、Pearson相似度算法。通过协同过滤的思想可以看出,用户的评分数据越多,计算出的相似度也高,推荐算法的效果也就越好[3]。但是,在实际应用中的推荐系统中,随着电子商务规模的不断扩大,用户的增加远远不及物品的增加,导致用户的评分矩阵极度稀疏,为了减小数据稀疏性问题对推荐算法效果的影响,赵长伟等提出了基于混合因子矩阵分解的推荐算法,有效缓解了数据稀疏性的问题[4];Li提出了一种基于用户-标签-项目的通过语义挖掘的算法,基于图模型和随机游走为基础,达到了不错的推荐的效果,却未使用到用户的评分[5],一般的基于用户的协同过滤算法仅仅使用用户共同评价过的项目的评分,并未利用到用户的全部评分,导致信息未得到充分的利用,影响了推荐算法的准确度。同时,由于用户的兴趣是随时间而变化的,不同年龄,不同阶段会有不同的兴趣偏好,本文提出了一种融合项目的子信息,利用到用户的全部评分数据,同时结合时间因素的协同过滤算法,实验结果显示,改进后的算法在精确度上较传统的协同过滤算法及只考虑项目类别的协同过滤算法上有明显的提升。
2 传统的UserCF算法
传统的User-based协同过滤算法过程主要如下。
步骤1):构建用户项目评分矩阵。将用户集合U={u1,u2,…,um}对项目集合I={I1,I2,…,In}的评分数据转化为用户项目评分矩阵R(m,n)中,如表1所示,rui表示用户u对项目i的评分,评分值可以是若干等级评分如0~5,也可以是0~1表示用户的某种行为如加入购物车、浏览等[6~7]。

表1 用户-项目评分矩阵
步骤2):计算用户之间相似度并确定邻居。根据用户项目评分矩阵计算相似度,从而找到与某个用户最相似的N个用户。常见的计算相似度的算法如下。
余弦相似度:

改进的余弦相似度[8]:
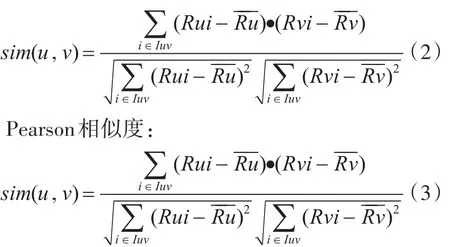
其中Iuv表示用户u和用户v共同评分过的项目,Rui表示用户u对项目i的评分,Rvi表示用户v对项目i的评分,表示用户v评分过项目的平均评分。
步骤3):为目标用户产生推荐。获取邻居用户v评分过,而目标用户u未评分的项目i,预测用户u对项目i的评分Pui。
采用的预测评分公式为

其中Nu为目标用户u的邻居集合,sim(u,v)即为步骤2)中用户u,v之间的相似度[9-10]。从传统的基于用户的协同过滤算法过程中可以看出,计算用户之间的相似度是整个算法的核心,而在实际中,用户间共同评分的项目很少,造成用户项目评分矩阵稀疏,影响了计算出来的相似性的精度。传统的协同过滤算法中只考虑了用户间共同评分的项目,而用户的其他项目的评分未得到使用,导致了用户评分信息未得到充分的利用,同时用户对每个项目评分时的时间、地点等上下文信息也没有得到利用,而这两个信息之间也是有紧密联系的。
3 融合用户对项目子信息兴趣变化的协同过滤算法
为了能充分利用用户的评分信息,本文考虑将用户评分的项目信息分解为更小的子信息,通过这些项目的子信息,充分挖掘用户对子信息的兴趣,发现用户深层次的偏好,从而找到相似度更精准的邻居。同时项目子信息划分必须保证项目子信息的种类必须有限个,同时能涵盖所有的项目。例如,给用户推荐计算机相关图书,根据图书内容信息,可将计算机图书分为 Java、Python、Linux、数据挖掘、Spark、人工智能、软件工程、大数据与云计算等有限个分类。如《Spark快速大数据分析》,基于其内容的子信息为Spark、大数据与云计算、人工智能等。基于内容的内部子信息可以更准确地描述项目同时也更容易区分不同的项目。
3.1 用户对项目子信息的偏好
假设项目子信息的分类集合为A={A1,A2,…,Ai,…,An},项目集合为I={I1,I2,…,Ij,…,Im},每个项目的子属性都包含在A中,所以推荐系统里面所有的项目特征信息可以用一个矩阵来表示,项目子信息矩阵表如表2所示,其中Cji表示项目j是否具备属性i,如果项目j含有属性i,Cji=1,如果项目j不含有属性i则Cji=0。


表2 项目-项目子属性矩阵

其中Puj表示用户u对子属性j的偏好程度,Pvj表示用户v对子属性j的偏好程度,表示用户u对所有子属性的平均喜好程度,表示用户v对所有子属性的平均喜好程度。
3.2 基于时间的用户兴趣度权重
由于用户的兴趣随着时间的变化而不断在改变,所以用户最近的评分更能反映用户最近的兴趣偏好,因此用户的不同时间的评分对相似度计算的影响是不同的,最近的评分的影响因子更大,应该被赋予更大的权重。根据用户在不同时刻的评分分配不同的权重的方式主要是有模拟遗忘曲线和时间窗技术。
遗忘曲线由德国心理学家艾宾浩斯提出,研究发现,遗忘在学习之后立即开始,而且遗忘的过程是不均匀的。最初遗忘的速度很快,后面逐渐缓慢。
时间窗技术就是研究如何划分有效的时间段来反映用户在这段时间的兴趣,因为我们通常认为用户的兴趣在一定时间段是稳定的[11]。
考虑到用户的兴趣变化与记忆遗忘有很大的相似处,本文借鉴艾宾浩斯遗忘曲线来描述用户的兴趣变化,基于时间的用户兴趣度权重函数如式(7)所示:

其中Tmax为用户评分的最晚时间,Tmin为用户评分的最早时间,t为当前评分时间,有e-1≤f(t)≤1。随着时间t的增大,f(t)逐渐增大,表明如果离评分时间越近,其分配的权重也就越大,越能反映用户的当前兴趣。
根据前面发现的用户对项目子属性的偏好,将时间权重引入基于项目子属性的用户相似度计算,发掘用户对项目子属性的兴趣偏好,用户u对项目子属性j的兴趣偏好为Puj如式(8)所示:

其中f(t)为时间遗忘函数,Cij即为项目i是否具备子属性j,Lui为用户u对项目i的评分。基本思想就是在计算用户u对子属性j的平均偏好程度时,引入时间权重,将每次对子属性的评分与对应时间的时间权重相乘,得到改进的用户对子属性的兴趣偏好计算方法,此时用户u、v的用户-项目子属性相似度计算公式为

传统的计算用户相似度的方法被广泛证明是有效的,为了提高推荐的精确度,本文结合用户-项目属性相似度和用户-项目子属性随时间变化的相似度,采用一个动态平衡因子α来改进用户-项目子属性相似度的计算,如式(10)所示:

3.3 算法步骤
融合用户对项目子信息兴趣变化的协同过滤算法流程如图1所示。
输入:数据集中一对训练集和测试集,平衡因子,最近邻居数K
输出:用户u对项目j的预测评分
算法步骤:
Step1:根据训练集得到用户-项目评分矩阵Rm×n;
Step2:采用Pearson相似度计算方法,计算基于项目评分的用户间的相似度simPearson(u,v);
Step3:分析项目子属性,确定子属性类别,构建项目-项目子属性矩阵Cmn;
Step4:引入时间权重f(t),计算用户对各子属性的对时间变化的偏好程度Puj(T);
Step5:计算基于项目子属性的用户兴趣随时间变化的用户相似度;
Step6:引入平衡因子 α,综合 simPearson(u,v)和simPT(u,v),得到改进的用户相似度 sim(u,v),并构建相似度矩阵;
Step7:根据Step6得到的相似度矩阵来寻找与目标用户u最近的K个邻居,选择sim(u,v)最大的预先设定的K个用户作为目标用户u的近邻;
Step8:根据Step7中确定的目标用户的近邻用户集合V和用户项目评分矩阵;
Rm×n,根据式预测目标用户u对项目j的评分;
算法结束。
4 实验设计与结果分析
4.1 实验数据
为了验证本文提出的融合用户对项目子信息兴趣变化的协同过滤算法的效果,本文采用著名的MovieLens网站提供的数据集,该网站上用户对观看过的电影评分,评分制为1~5分,最低为1分,最高为5分,评分越高表示用户对改电影越喜欢,同时电影分为恐怖,冒险,幻想,动作,动画,戏剧,喜剧,儿童,犯罪,纪录片,黑色电影,音乐剧,爱情,悬疑,科幻,惊悚,战争和西方18个类型[12],由于每个电影可以同时涵盖几种类别,同时电影类别也满足我们提出的项目子属性的要求,所以将电影类别作为电影项目的子属性,方便我们不用再去寻找隐藏的子属性,更容易去验证本文提出的算法的效果。
本文选取MovieLens-1MB数据集,该数据集包含6040个用户对3900部电影的1000209个评分,训练集合采用随机选取的办法,例如:训练集占整体数据集比重为X,则测试集占整体数据集的比重为1-X,当X=0.8时,训练集所占比重为80%,测试集占比为20%,此时数据稀疏度为95.53%。
4.2 评价指标
由于推荐系统的应用场景不同,所以推荐系统在不同方面有不同的评价指标,这些指标有的可以定量计算,有些只能定性描述,有些可以通过离线实验计算,有些需要通过用户调查获得,还有些只能在线评测。对推荐效果的评价主要分为三种类型:准确性、多样性、新颖性。
本文以准确性为评价指标,根据平均绝对误差(Mean Absolute Error,MAE)[13~14]来计算推荐系统产生的预测与用户实际评分的误差,以此来衡量推荐结果的准确性,平均绝对误差MAE公式为
对于测试集中的一个用户u和物品i,令rui是用户u对物品i的实际评分,而r̂ui是推荐算法给出的预测评分。MAE越小,表示推荐的精度越高[15]。
4.3 实验结果分析
实验1:选择X=0.8,即数据集的80%作为训练集,20%作为测试集,首先根据传统的推荐算法得到MAE值最小时的K值,从图2可以看出当K值为35时,传统算法下平均绝对误差值最小,因此我们选择K为35,以便接下来的研究。

图2 不同平衡因子下的MAE
实验2:选择K值为35,测试不同平衡因子对改进的推荐算法的精准度的影响,实验结果如图3所示,当平衡因子为为0.2时,改进的推荐算法下的平均绝对误差最小。

图3 不同K值下的MAE
实验3:此时,选取平衡因子=0.2,对不同K值下的传统推荐算法和本文提出的改进的推荐算法的效果进行比较。结果如图4所示,实验结果显示,改进的推荐算法在不同K值下的预测评分精准度均高于传统的基于Pearson相似度计算的推荐算法,且本文提出的改进算法在平衡因子为0.2,最近邻居为30时,评分预测的平均误差最小,推荐的效果达到最优。

图4 不同K值下两种算法下的MAE
5 结语
本文通过试验设计,探讨了融合用户对项目子信息兴趣变化的协同过滤算法的推荐性能。介绍了从基于用户-项目子属性的随时间变化的兴趣偏好的设计思路以及实验步骤,直到确定了一些重要参数如平衡因子和最近邻居数值K,最后将本文提出的改进的推荐算法与传统的算法效果进行比较。研究发现,当平衡因子为0.2时,融合用户对项目子信息兴趣变化的协同过滤算法推荐的效果最好,当邻居数小于30时,该算法的推荐质量随着最近邻居数的增大而增大,当邻居数大于30后,改算法的推荐质量随着最近邻居数的增大而缓慢减小并趋于平稳。在算法的整体精准度的比较上,本文提出的推荐算法的MAE值都小于传统的基于Pear⁃son相似度计算的推荐算法,在数据稀疏性问题上,本文提出的改进算法的推荐效果更好。
