具有逆断面的正则半群上与格林关系有关的同余

2021-11-09冯莹莹

华南师范大学学报（自然科学版） 2021年5期

冯莹莹, 商宇

(1. 佛山科学技术学院数学与大数据学院, 佛山 528000; 2. 普洱学院数学与统计学院, 普洱 665000)

具有逆断面的正则半群[1]因具有相对集中的逆子半群的结构而备受关注,断面的概念也在不断拓展[2-4]. 1989 年，SAITO[5]给出了具有逆断面的正则半群的结构定理:具有逆断面的正则半群S由3个构件(I、S°和Λ)组成,其中S°是S的逆子半群. 1997年,TANG[6]指出,对于一般的具有逆断面的正则半群来说,I、Λ都是S的子半群,而且I、Λ分别为左正则带、右正则带. 此后,I、Λ、S°以及包含I和S°的左逆子半群L、包含Λ和S°的右逆子半群R成为了学者们比较关注的正则半群S的重要的子半群[6-7].

格林关系在半群的结构中起着重要的作用,在正则半群中更是如此, 如BLYTH和ALMEIDA SANTOS[8]利用格林关系对具有逆断面的正则半群进行分类. 同余在一般半群或正则半群上也有类似的作用,如：HOWIE和LALLEMENT[9]证明了由格林关系生成的同余*和由格林关系生成的同余*是相等的,且*=*是正则半群S上的最小半格同余;PASTIJN和PETRICH[10]确定了格林关系、、所生成的同余*、*、*和格林关系、、在幂等元集E上的限制所生成的同余 (|E)*、(|E)*、(|E)*所对应的半群类, 从而刻画了由它们所生成的同余子格.

在一般的正则半群上,PASTIJN和PETRICH[10]给出了由格林关系所生成的同余和由格林关系在幂等元集E上的限制所生成的同余的一般描述;在特殊的正则半群上,冯莹莹和汪立民[11]更精细地刻画了由格林关系所生成的同余和由格林关系在幂等元集E上的限制所生成的同余. 幂等元集E是正则半群的重要子集,而I、Λ、S°、L、R是具有逆断面的正则半群的重要子半群. 本文研究在具有逆断面的正则半群上,由格林关系所生成的同余和由格林关系在子半群I、S°、Λ、L、R上的限制所生成的同余,确定它们所对应的半群类,从而刻画由它们所生成的同余子格.

1 预备知识

设S是半群,记S的幂等元集为E(S),或简记为E.S上的恒等关系记为ε.S上的等价关系格和同余格分别记为(S)和(S). 设{,,},ρ(S),A是S的子集,记Aρ={aρ|aA},E(A)={eA|e2=e},分别记由和|A生成的同余为*和(|A)*.S和S/ρ上的格林关系分别记为和S/ρ. 若A是S的子半群,则记A上的-关系为A. 设aS,记V(a)={xS|axa=a,xax=x}为a的逆元集.

设S是正则半群,S°是S的逆子半群,如果对S中的任一个元x,x在S°中有且仅有一个逆元,即|V(x)∩S°|=1,则称S°是S的逆断面. 如果S°还是S的拟理想,即S°SS°⊆S°,则称S°为S的Q-逆断面.x在S°中的唯一的逆元记为x°. 记(x°)°为x°°. 于是,x°°°=x°. 若X是S的子集,记X°={x°S°|xX}. 本文中,如无特别声明,S均指具有逆断面S°的正则半群.

下面给出具有逆断面的正则半群的运算和子半群方面已有的结论.

结论1[7]设S是具有逆断面的正则半群,则对任意x,yS,有

(1)(xy)°=y°(xyy°)°=(x°xy)°x°=y°(x°xyy°)°x°;

(2) (xy°)°=y°°x°.

结论2[12]设S是具有逆断面的正则半群,则S是纯正的当且仅当对任意x,yS,(xy)°=y°x°.

结论3[6-7]设S是具有逆断面的正则半群,则

(1)I={xS|x=xx°}={xx°|xS}是左正则带,Λ={xS|x=x°x}={x°x|xS}是右正则带;I、Λ具有公共逆断面E(S°),且I∩Λ=E(S°);

(2)L={xS|x=xx°x°°}={xx°x°°|xS}是左逆半群,R={xS|x=x°°x°x}={x°°x°x|xS}是右逆半群;E(L)=I,E(R)=Λ;L、R具有公共逆断面S°,且L∩R=S°,I∩R=L∩Λ=E(S°).

具有逆断面的正则半群S的这几个子半群之间的关系可用图 1 表示.

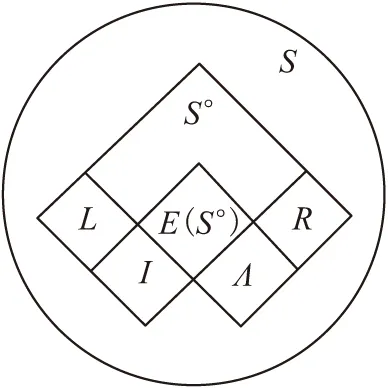
图1 几个子半群之间的关系

结论4[13]设S是具有逆断面S°的正则半群,ρ是S上的同余,则S°/ρ°≃S°ρ是S/ρ的逆断面,其中ρ°=ρ|S°.

我们知道,把握正则半群主要是在格林关系的框架下,利用幂等元和逆元来确定元素及其乘积的位置. 利用格林关系,可以定义如下几种半群类:

(1)左正则带[14]. 如果带S上=,则称S为左正则带. 左正则带还有2种等价的定义方式:一种是带S上=ε;另一种是对任意a,xS,axa=ax.

(2)右正则带[14]. 如果带S上=,则称S为右正则带. 等价地,设S是带,如果对任意a,xS,axa=xa,那么称S是右正则带.

(3)正则带[14]. 如果带S是一个左正则带和一个右正则带的次直积,则称S是正则带. 等价地,设S是带,如果对任意a,x,yS,axya=axaya,那么称S是正则带.

(4)左逆半群[10]. 如果S是纯正半群,且幂等元集E(S)是左正则带,则称S是左逆半群. 这类半群有时也称作R-unipotent的,因为它的每个-类有且只有一个幂等元.

(5)右逆半群[10]. 如果S是纯正半群,且幂等元集E(S)是右正则带,则称S是右逆半群. 这类半群有时也称为L-unipotent的,因为它的每个-类有且只有一个幂等元.

(6)拟逆半群[10]. 幂等元集是正则带的纯正半群称为拟逆半群. 半群S是拟逆半群当且仅当S是正则半群,且是一个左逆半群和一个右逆半群的次直积.

一般地，常用LRB表示左正则带，用RRB表示右正则带，用RB表示正则带，用LI表示左逆半群，用RI表示右逆半群，用QI表示拟逆半群，用S表示半格，用I表示逆半群. 值得注意的是，上面所列举的半群均保持同态像[14]，即若A为上述所列举的其中一种半群类，ρ是A-半群S上的同余，则S/ρ仍为A-半群. 设A是某半群类，ρ是半群S上的同余，如果ρ是使S/ρA的最小同余,那么称ρ是最小A-同余.

PASTIJN和 PETRICH[10]确定了由格林关系和格林关系在幂等元集E上的限制所生成的同余所对应的半群类.

结论5[10]设S是正则半群,则

2 主要结果

首先,给出具有逆断面的正则半群的一些性质;然后,考虑与格林关系有关的同余所对应的商半群所属的类型.

命题1设S是具有逆断面S°的正则半群,x,yS,则xyxx°=yy°,xyx°x=y°y.

证明设xy,则xx°xyyy°. 由于xx°,yy°I,I是左正则带,左正则带上=ε,故xx°=yy°. 反之,若xx°=yy°,则xxx°=yy°y,从而xy. 类似可证xyx°x=y°y. 证毕.

下面考虑商半群S/ρ的几个特殊子半群中元素的提升性. 为免符号混淆,记S/ρ的子半群I、L分别为I(S/ρ)、L(S/ρ),而S的子半群I、L仍记为I、L.

命题2设ρ是具有逆断面的正则半群S上的同余,aS，有如下结论：

(1) 若aρI(S/ρ),则存在eI,使得aρ=eρ;

(2) 若aρ(S/ρ)°,则存在x°S°,使得aρ=x°ρ;

(3) 若aρE((S/ρ)°),则存在e°E(S°),使得aρ=e°ρ;

(4) 若aρL(S/ρ),则存在xL,使得aρ=xρ.

证明对任意aS,(aρ)°=a°ρ，可得

(1)若aρI(S/ρ),则

aρ=(aρ)(aρ)°=(aρ)(a°ρ)=(aa°)ρ.

于是，aa°I,且aρ=(aa°)ρ.

(2)若aρ(S/ρ)°,则aρ=(aρ)°°=(a°°)ρ. 故a°°S°,且aρ=a°°ρ.

(3)若aρE((S/ρ)°)⊆I(S/ρ),由(1)的证明过程知aρ=(aa°)ρ. 又,aρE((S/ρ)°),所以aρ=(aρ)°=((aa°)ρ)°=(a°°a°)ρ. 故a°°a°E(S°)且aρ=(a°°a°)ρ.

(4)若aρL(S/ρ),则aρ=(aρ)(aρ)°(aρ)°°=(aρ)(a°ρ)(a°ρ)°=(aρ)(a°ρ)(a°°ρ)=(aa°a°°)ρ. 于是aa°a°°L,且aρ=(aa°a°°)ρ. 证毕.

下面考虑S的同态像中格林关系和°-关系的提升性.

命题3设S是具有逆断面S°的正则半群,ρ是S上的同余,A,BS/ρ且A=B°,则存在aA,bB,使得a=b°.

证明设B=bρ,令a=b°,则aρ=b°ρ=(bρ)°=B°=A,故aA,bB且a=b°. 证毕.

命题4设S是具有逆断面S°的正则半群,ρ(S),有如下结论:

(1)若A1,A2I(S/ρ)且A1A2,则存在u1A1∩I,u2A2∩I,使得u1u2;

(2)若A1,A2(S/ρ)°且A1A2,则存在u1A1∩S°,u2A2∩S°,使得u1u2.

证明(1)因为A1,A2I(S/ρ),由命题2(1),存在x1,x2I,使得x1ρ=A1,x2ρ=A2. 令则从而u1u2.

因为A1A2,由命题而A1,A2I(S/ρ),故于是u1u2因为x1,x2I,所以从而IE(S°)⊆I. 综上可知,u1A1∩I,u2A2∩I,且u1u2.

(2)因为A1,A2(S/ρ)°,由命题2(2),存在x1,x2S°,使得x1ρ=A1,x2ρ=A2. 令则从而u1u2.

因为A1A2,所以于是

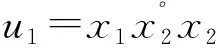
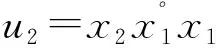
因为x1,x2S°,所以u1,u2S°. 综上,u1A1∩S°,u2A2∩S°,且u1u2. 证毕.

对具有逆断面的正则半群,右逆半群与右正则带有更简洁的刻画方式.

引理1设S是具有逆断面的正则半群,则下列各条件等价:

(1)S是右逆半群;

(2)I=E(S°);

证明(1)、(2)等价在文献[8]中已证. 下证 (2)⟺(3).

(2)⟹(3). 因为I=E(S°)是半格,所以,|I=|E(S°)=εE(S°)=εI.

(3)⟹(2). 对任意eI,ee°e=e°;又,eI,e°E(S°)⊆I,|I=εI,所以e=e°E(S°),I⊆E(S°),从而I=E(S°). 证毕.

引理2设S是具有逆断面的正则半群,则S是右正则带当且仅当L=E(S°).

证明若S是右正则带,则对任意xx°x°°L,(xx°)x°°=(x°xx°)x°°=x°x°°E(S°),于是L⊆E(S°),从而L=E(S°). 若L=E(S°),则对任意sS,s=(ss°s°°)(s°s)LΛ=E(S°)Λ⊆Λ,于是S⊆Λ,从而S=Λ是右正则带. 证毕.

设S是具有逆断面S°的正则半群,如果S°是半格,则称S是具有半格断面的. 记这类半群为ST.下面考虑具有半格断面的正则半群与逆半群、右逆半群和拟逆半群类之间的关系.

引理3在具有逆断面的正则半群类中,

(1)I∩ST=S;

(2)RI∩ST=RRB;

(3)QI∩ST=RB.

证明(1) 设S既是逆半群,又是具有半格断面的正则半群. 因为S是逆半群,所以S=S°;又,S具有半格断面,由文献[15]的引理2.3可知S°=E(S°). 于是,S=E(S°)是半格. 反之,易证半格既是逆半群,又是具有半格断面的正则半群.

(2)若S既是右逆半群,又是具有半格断面的正则半群,则由引理1及文献[15]的引理2.3,有I=E(S°)=S°. 因此,对任意sS,s=(ss°)s°°(s°s)IS°Λ=E(S°)E(S°)Λ⊆ΛΛΛ=Λ,从而S⊆Λ,进而S=Λ是右正则带. 反之,易证具有逆断面的右正则带既是右逆半群,又是具有半格断面的正则半群.

(3)设S是具有半格断面的拟逆半群,则S°=E(S°). 于是,对任意xS,有

x=xx°x=(xx°)x°x=(xx°)(x°x)x°(xx°)x=

(xx°)(x°x)(xx°)x°(xx°)x=xx,

所以S是带. 又,S是拟逆半群,E(S)是正则带,于是S=E(S)是正则带. 反之,若S是具有逆断面的正则带,则S是拟逆半群,且S°是带. 又,S°是逆半群,幂等元是交换的,所以S°是半格,从而S是具有半格断面的拟逆半群. 证毕.

引理4设T是半群S的子半群,则(ε|T)*=ε.

证明显然,ε|T⊆ε,从而(ε|T)*⊆ε,于是,(ε|T)*=ε. 证毕.

下面给出本文的主要结论.

定理1设S是具有逆断面S°的正则半群,则

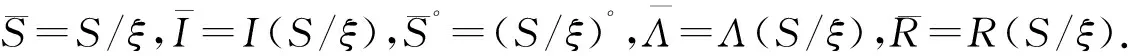
(1)设x(|I)*,y(|I)*S/(|I)*,且(x(|I)*)|I)*). 由命题4,存在a,bI,使得a(|I)*x,b(|I)*y,且a|Ib. 则x(|I)*a|Ib(|I)*y,从而x(|I)*=y(|I)*. 由引理1,(|I)*是右逆同余. 设ρ是一右逆同余,e,fI且e|If,则(eρ)|I(S/ρ)(fρ). 由引理1,eρ=fρ,从而|I⊆ρ,进而(|I)*⊆ρ. 于是,(|I)*是最小右逆同余. 再由命题1后的论述及文献[10]的定理1(iii)知,(|I)*=(|I)*=(|E)*是最小右逆同余.