巧用几何画板，实施数学教学

张兵 张会

【摘要】被称为21世纪的动态几何——“几何画板”是一种能动态展现出几何对象的位置关系、运行变化规律的优秀的教育软件。它顺应时代发展，是数学教师组织学生学习数学的好帮手。笔者将结合自己的教学实践，从课前、课中、课后三个方面来阐述如何巧用几何画板，实施数学教学。课前巧用几何画板，可以优化数学课堂;课中巧用几何画板，可以突破认知难关;课后巧用几何画板，可以及时反馈教学效果。在教学新课时合理利用几何画板，可以补充教学内容，强化学生的感性思维;可以突破教学难点，发展学生的抽象思维。

【关键词】巧用 几何画板 数学教学

数学课程标准指出：“信息技术的发展对数学教育的价值、目标、内容以及教学方式产生了很大的影响。”几何画板利用点、线、面构造图形，具有动态性、朴实性和简洁性的特点，为广大数学教师和学生所喜欢。巧用几何画板，可将数学教学由静态的、抽象的、枯燥的化为动态的、形象的、有趣的，从而让教师教得轻松，学生学得愉快。

一、课前巧用几何画板，优化数学课堂

数学知识，特别是新旧知识之间有着密切的联系，表现出很强的系统性。旧知识是新知识的基础，新知识又是旧知识的延续和深入。学生学习数学知识的过程实际上就是在新知识与已有认知结构中的旧知识之间建立联系的过程。如何找到新旧知识之间的切入点，让学生感到新知识新而不难呢？一般的教学模式都是通过提问、练习等教学活动，从旧知识过渡到新知识。但模式比较单一，不够新颖，学生学习兴趣不高。因此在教学新课前，笔者尝试利用几何画板制作的课件，让学生在玩中学，在学中玩，从而感到数学真的很“好玩”。

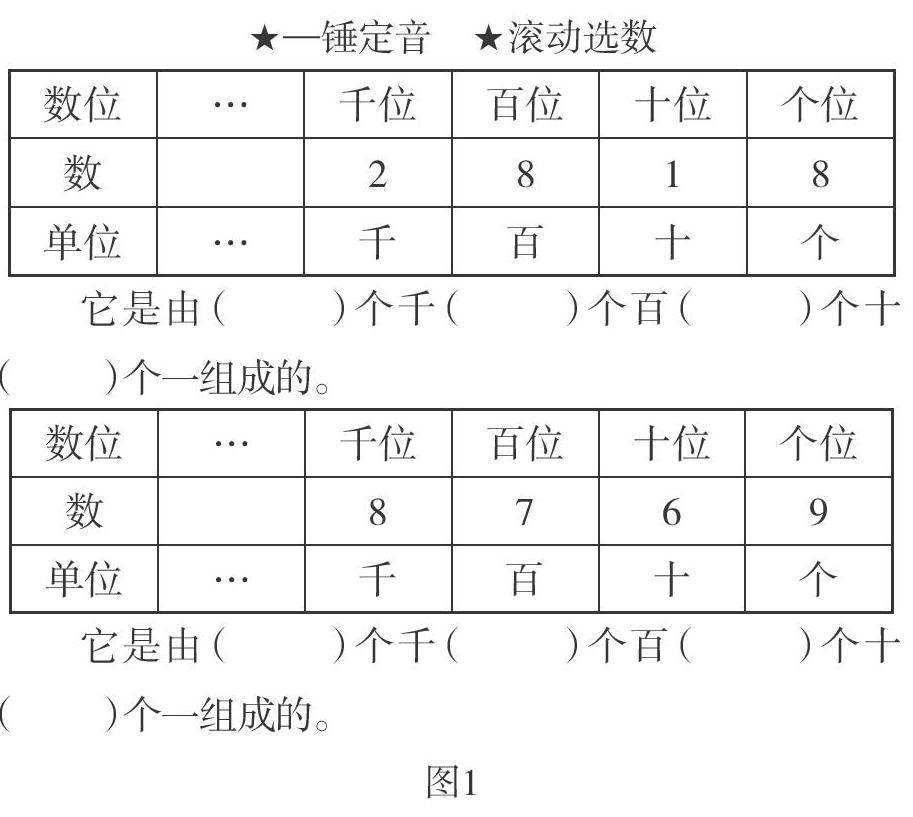
例如，北师大版数学二年级下册第一单元的教学内容，包括数数、读数、写数、数的组成、数位的含义等。这些内容对于低年级的学生来说是比较枯燥无味的。为了让学生熟练地掌握这些知识点，为后面学习更大的计数单位“万”、认识更大的数打好基础，笔者决定打破常规教学模式进行教学。在上课伊始，打开课件“万以内数的认识”，如图1所示，点击右上角“滚动选数”按钮，表格中的四位数就会不停地滚动，发生变化，只要说“停”，再点击一次，表格中的四位数就固定不动了。学生们各个都带着好奇的眼光、不断求索的欲望，很快地根据数位表，读出这个四位数，说出数的组成。

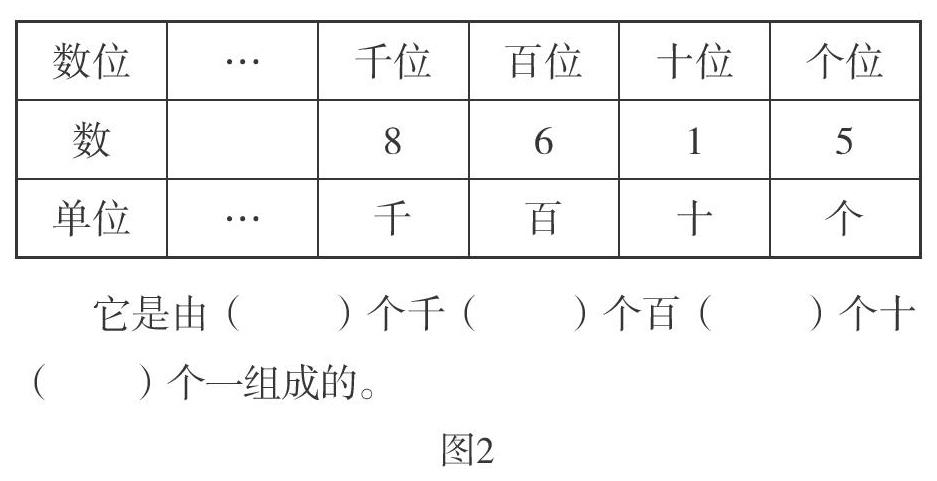
如果点击左上角“一锤定音”按钮，如图2所示，表格中的数就会变化一次，学生根據数位表就会很快读出这个四位数，说出它的组成。

这个利用几何画板制作的课件，就是以动态的效果展示不同的四位数，将趣味性和知识性巧妙地融为一体。学生在反复练习中巩固了所学的知识，却又乐此不疲，为后面的新知学习做了很好的铺垫，从而优化了数学教学。

二、课中巧用几何画板，突破认知难关

1.利用几何画板，可以补充教学内容，强化感性思维

心理学研究表明，小学生的思维正处在从具体形象思维向抽象思维过渡的阶段。在小学数学教学中，笔者发现利用几何画板这一软件制作出一些动态的课件，可以很好地对教材内容进行补充，有效地实现对学生感性思维的强化。

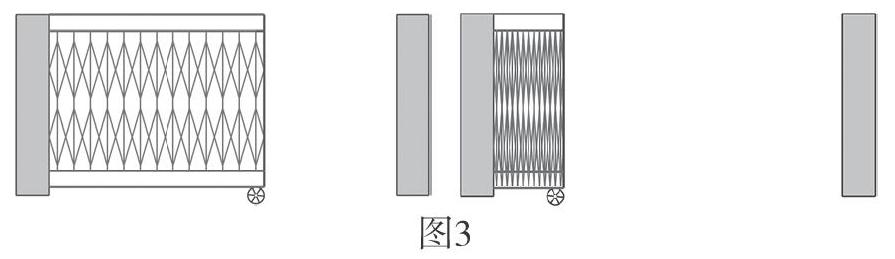
下面以北师大版数学四年级下册第二单元第一课时的内容为例。这一课时的内容是在给图形进行分类之后，学生知道了三角形和四边形都属于平面图形，知道了三角形和四边形在边和角数量上的不同，为了进一步让学生了解三角形和四边形的特性的区别：三角形具有稳定性，而平行四边形不具有稳定性，容易变形。在传统的教学中，教师一般都会让学生用小棒自制学具“三角形”和“平行四边形”，从而感受它们的特性区别。然而它们的这一特性在生活中有哪些应用呢？课后习题中有关三角形的稳定性给出了很多实例，如牙签桥、椅子的三角形支架等。在有关平行四边形的易变性教学中，教师只能让学生想象回忆，举生活中的例子。笔者利用几何画板制作的课件“伸缩门演示”，丰富了学生的感性认识，让学生目睹了平行四边形的易变性。

打开课件“伸缩门演示”（如图3），点击课件左上角的“开门”按钮，门就自然地打开。要想使门停止，只要再点击一次“开门”按钮，门就自动停住，门上面的“平行四边形”也就自动地收缩起来了。

再点击课件左上角的“关门”按钮（如图4），门就自然地关上，门上面的“平行四边形”就自动地伸展开来。

课件“伸缩门演示”对教学中的知识点做了很好的补充。通过伸缩门的开与关，让学生直观地看到了平行四边形的易变性在生活中的应用，从而更牢固地掌握知识。学生在动态中感受了平行四边形不具有稳定性、容易变形的特性，同时感受到数学知识来源于生活，又应用于生活。

2.利用几何画板，可以突破教学难点，发展抽象思维

教学难点是从学生的角度来说的，教师在备课时，不光要备教材，更要备学生。对于学生较难理解和掌握的教学内容，教师就要多花点时间和心思去钻研、去创新，用一种学生易接受的方式去讲解，才能收到良好的教学效果。在实际教学中，遇到教学难点问题，笔者往往会开动脑筋，利用几何画板制作的课件，突破难点，发展学生的抽象思维。下面以北师大版数学四年级下册第二单元的第二课时内容为例。

教材中依照三角形中最大角的类别将三角形划分为锐角三角形、钝角三角形、直角三角形，同时根据边的特点又提出了等腰三角形与等边三角形的概念。笔者在这些教材内容的基础上，采用动态变换的形式演示了按最大角进行分类的情况。

打开课件“三角形分类演示”，如图5所示，拖动点A（或其他点）可改变三角形的形状，图形下方自动给出三角形类别的文字说明，同时三角形内部色彩也发生着变化。当最大角等于73°时，三角形下方就出现“锐角三角形”，颜色是黄色的。

继续拖动点A（或其他点），如图6。当最大角等于90°时，三角形下方就出现“直角三角形”，随着三角形形状的改变，颜色变成浅绿色的。

接着按上述方法，拖动点A（或其他点），如图7，当最大角等于100°时，三角形下方就出现“钝角三角形”，随着三角形形状的改变，颜色又变成肉红色了。

利用几何画板制作的这个课件直接用于课堂教学中，可以有效地激发学生学习的兴趣。就这样，学生不再机械地去记忆数学知识，而是通过直观的变换的形式去观察、分析、理解、掌握，抽象思维逐步发展起来。

三、课后巧用几何画板，及时反馈教学效果

每次新课教学之后，笔者有一个习惯，总要给学生留几道与本节课知识点相关的习题。一方面，了解学生对知识点的掌握情况;另一方面，提高学生思维的灵活性和转变能力。记得在学完“整数乘法”这部分内容之后遇到了一道植树问题。教师一般都会鼓励学生画图来帮助理解，但学生能举一反三吗？能让学生一目了然地发现不同的植树要求就存在不同的计算方法吗？于是为了便于学生理解，发现其中的规律，笔者利用几何画板，把静止不动的植树问题变成鲜活灵动的植树场景，把学生带入其中，进而轻而易举地解决问题。笔者将植树问题归于三种情况，一种环形植树问题，一种两端都栽的植树问题，一种一端不栽或两端都不栽的植树问题。

笔者先打开课件“环形植树”，点击左上角“植树了”和“数间隔”按钮，如图8，当植了4棵树，让学生数间隔数为4;当植了8棵树，让学生数间隔数为8;当植了12棵树，让学生数间隔数为12……

最后让学生从“变化”中找出“不变”：间隔数=棵数，就这样，问题得到了解决。

之后笔者又出示了课件“（两端都栽）植树问题”，如图9。学生很快得出“间隔数=棵数-1”的规律，计算也就迎刃而解。

同样，在一端栽树的情况下，出示课件“植树问题（只栽一端）”，如图10，学生们很快得出了“间隔数=棵数”。

在教学新课之后，如果能巧妙运用几何画板，就可以及时反馈教学效果，教师也能及时做出反应，调整课堂教学进度和节奏。

“学习的本质不是被动地形成‘刺激—反应的联结，而是主动地形成认知结构。”作为一线数学教师，应该根据实际情况，合理运用现代信息技术，把现代信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式，使学生乐意并有可能投入现实的、探索性的数学活动中。实践证明，实施数学教学巧用几何画板，是一种不错的选择！