以微带面 精准教学*——高三二轮复习课“立体几何中的作图问题”教学实录与感悟

蔡海涛

(福建省莆田第二中学，351131)

2019年4月2日-4日,福建省第三批高中数学基地学校研讨活动在厦门集美中学举行.研讨的主题是解决高中数学教育教学实践中存在的重难点问题,提升教育质量.会议期间，笔者应邀开设了一节高三微专题复习课“立体几何中的作图问题”.现将这节课的教学过程、设计意图、课后感悟整理成文,以期抛砖引玉.

一、教学过程

1. 切入主题

师:我们知道解决立体几何问题需要一定的空间想象能力，研究往往从图形开始，这就要求我们要有识图、作图、用图的能力.作图问题就是定性几何图形的位置关系，而在立体几何中最重要的位置关系就是平行和垂直.今天就和同学们一起来研究立体几何中涉及平行和垂直的作图问题.

设计意图开门见山,直奔主题,提高课堂效率,符合高三数学复习课的特点,同时让学生感受学习这节课的必要性，提升学习的兴趣.

2. 平行问题

师:请同学们看例1,先考虑第1小题.

例1(人教A版必修2第63页B组第1题改编)一三棱锥形木块如图1所示,点P在平面VAC内,D、E分别为棱AB、VB中点.

(1)过点P和直线DE将木块锯开,应该怎样画线?

(2)过点P将木块锯开，使截面平行于直线VB和AC，应怎样画线?

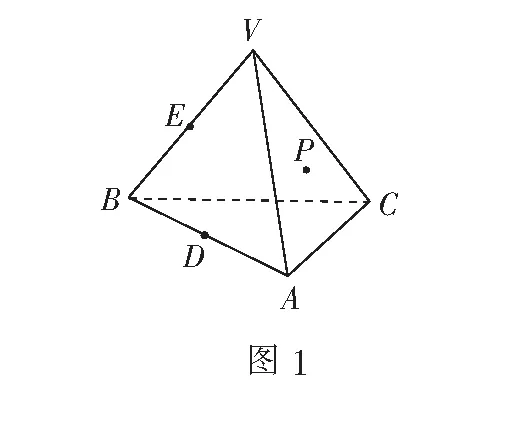
生1:点P和DE确定一个平面，连结PD,PE,DE,即为所求画线.

师:P、D、E三点共面,但题意要求的画线是画在如图1三棱锥(木块)的表面上,所以实质上是要画出平面PDE与三棱锥表面的交线，直线PD,PE就不符合要求了.那么我们该怎么画呢?

生2:过点P作MN平行于VA，交AC于M，交VC于N，连结DM、NE、ED，即为所求画线.

师:回答正确，你是怎么想到的?

生2:首先注意到DE与平面VAC平行.根据线面平行的性质，平面PDE与平面VAC的交线与直线DE平行，又因为DE∥VA，所以作VA的平行线MN，然后再连结D、M、N、E各点就好了.

师:非常好,画两个平面的交线,常常要观察线面平行的关系,根据线面平行的性质,得到两平面的交线.另外，同学们在过一点作已知直线的平行线时，要在同一个平面内作出，本题如过点P作MN平行DE就不合理了.接下来请同学们看第2小题.

生3:过点P作FG平行AC，交VC于F，交VA于G；过点G作GH平行VB，交AB于H；过点H作HI平行AC，交BC于I，连结IF，则平面FGHI即为所求.

教师投影例1的解答过程.

设计意图引导学生初步感受立体几何中的作图问题，明确几何作图的每个环节都需要有理有据.涉及平行关系的作图问题，一般根据平行的性质，来寻找求解问题的途径.

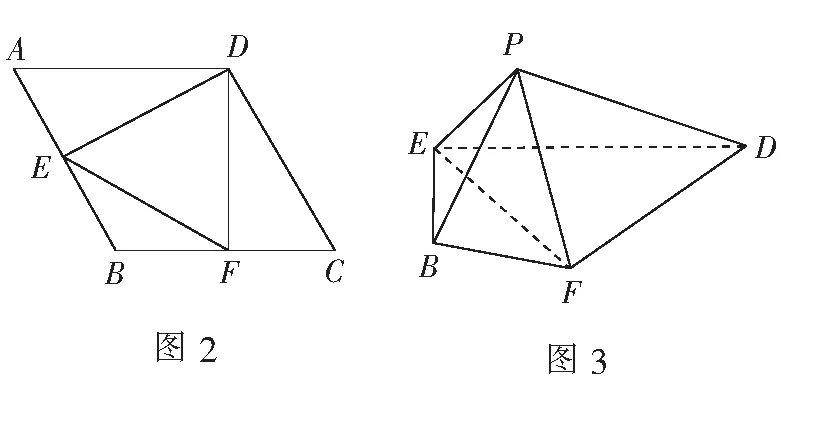
变式如图2,边长为2的菱形ABCD中，E,F分别是AB,BC的中点.将∆DAE,∆DCF分别沿DE,DF折起,使A,C重合于点P,如图3.在棱PD上找点G,使得PB∥平面EFG,并说明理由.

学生思考、练习后,教师投影生4的解答:

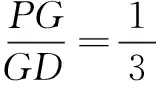
如图4、5,在菱形ABCD中,连结AC,BD设BD∩EF=O,BD∩AC=M.

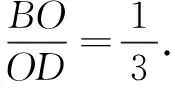
因为OG⊂平面EFG,PB⊄平面EFG,所以PB∥平面EFG.

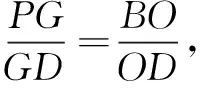
师:对于探究性问题,一般是先假设结论成立,通过这个结论来发现性质,确定几何图形的特征.

设计意图通过例1及例1变式，分析这两道题中立几作图平行问题的共性，都是从平行关系的性质入手，确定几何图形的位置关系，然后再作出图形.

3. 垂直问题

师:请同学们看例2,先完成第(1)问.

例2如图6,长方体ABCD-A1B1C1D1中，AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,面A1C1上有一点O.

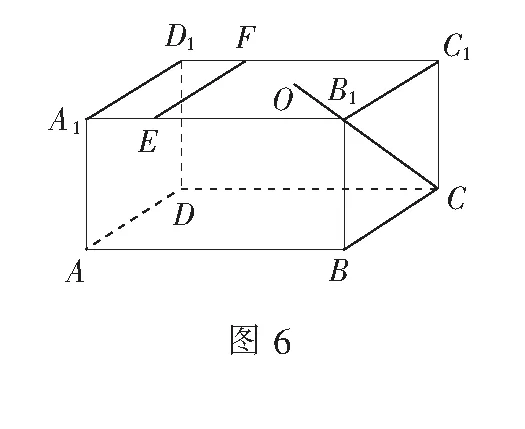
(1)(人教A版必修二78页B组第1题改编)经过点O在平面A1C1上画一条直线与直线CO垂直；

(2)(2015年高考全国Ⅱ卷·理19)过点E,F的平面α与此长方体的面相交,交线围成一个正方形,在图中画出这个正方形(不必说出画法和理由).

生5:在(1)问中，连结OC1，在面A1C1上，过点O作一直线与OC1垂直，即为所求.

师:(追问)你是如何利用已有的垂直关系作图的?

生5:首先发现CC1⊥平面A1C1，所以所求直线必与平面CC1O垂直，因此只需在面A1C1上作OC1垂线即可.

师:非常好.对于垂直关系的作图，与平行关系的作图类似，也是先去寻找原有的位置关系，再利用性质解题.这道题关键就是要发现CC1⊥平面A1C1，然后去构造垂直(过点O作一直线与OC1垂直),从而得到新的线面垂直关系(所求直线垂直平面CC1O),再得到所求直线垂直CO.

设计意图例2的解题策略是寻找已有线面垂直关系，构造线线垂直，得到新的线面垂直关系.这种方法也是经过平面α外一定点P向平面α内一条定直线AB引垂线的常用方法.即先经过P点作平面PO⊥α于O,再过O作OH⊥AB于H,连结PH，为所求该模型，即三垂线定理的模型.

(片刻后)投影生6例2第(2)的解答:

解(2)交线围成正方形EHGF，如图7.

师:(追问)你确定你所画的图形是正方形？点H在什么位置?

生6:因为平面AC∥平面A1C1，平面AB1∥平面DC1，所以平面α与此长方体的面相交的交线围成的四边形为平行四边形，又EF垂直平面AB1，所以该平行四边形为矩形.因此只需考虑EF=EH=10，即满足题意在矩形ABB1A1中，可求得AH=10.

师:很好.作长方体截面，要充分利用平行垂直关系，先判断截面图形的形状确定位置关系再确定长度(角度).

设计意图涉及垂直关系问题的作图，引导学生观察已有的垂直关系，通过在某个平面作线线垂直，得到新的线线垂直或线面垂直，即一般通过线面垂直与线线垂直关系的互相转化来处理.

4. 巩固提升

练习(2019年福州市高三质检·文19)如图8,四棱锥E-ABCD,平面ABCD⊥平面ABE,四边形ABCD为矩形,AD=6,AB=5,BE=3,F为CE上的点,且BF⊥平面ACE.

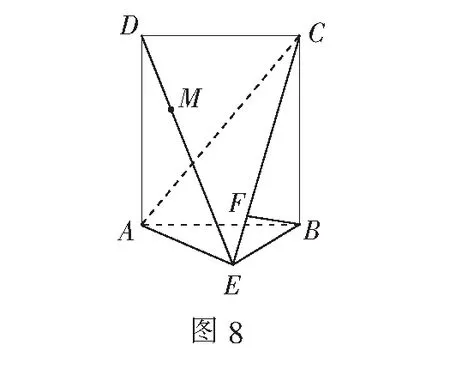
(1)求证:AE⊥BE;(略)

(2)设M在线段DE上,且满足EM=2MD,试在线段AB上确定一点N,使得MN∥平面BCE,并求MN的长.

学生练习过程略.

设计意图通过练习，进一步提升同学们立几作图的能力，引导学生归纳平行与垂直的作图的一般方法.作图方法的多样性可引导学生多角度思考问题.

5. 归纳总结

师:请同学们交流总结下本节课的学习心得.

生交流总结:通过本节课的学习，我们体会到立体几何中如何更好地识图、作图、用图，如何利用平行、垂直的性质去解决涉及平行、垂直的作图问题，在作图中提升空间想象能力，书写中提升推理论证能力.

二、 教学感悟

1. 微专题究竟微在哪？

高三二轮专题复习中,教师通常围绕热点问题开展微专题复习.“微专题”的“微”要立足学生的学情(学生哪个模块哪个类型题目比较薄弱？为什么比较薄弱？),要求切口小、针对性强.只有“微”到点上,才能做到精准教学,复习高效[1].本节课围绕“立体几何中的作图问题”设计教学,利用平行和垂直两种关系的作图,讲明作图的原理,培养模型意识,涵盖了立体几何中线线、线面、面面平行垂直关系的转化,培养了空间想象、推理论证等能力,发展了数学抽象、直观想象、逻辑推理、数学运算的数学学科核心素养,起到了以微带面的效果.

2. 高三复习应回归教材

在高考中,立体几何的作图题多次出现,如2018年全国Ⅲ卷文科第19题,2016年全国I卷文科第18题;2016年四川卷理科第18题;2013年福建卷理科第19题;2013年福建卷文科第18题;2013年湖北卷理科第19题;2013年四川卷理科第19题,文科第19题;2013年安徽卷理科第15题、文科第15题;2009年安徽卷理科第18题;2002年全国卷文科第22题等.这些作图题蕴含着空间想象，推理论证,考查了立体几何中最重要的两项基本功.所以说高三立体几何的备考一定要落在“基础”上,要回归教材.基于此,笔者在例题的选择上，都是以课本的例题为母题,然后再进行变式.通过变式,可以发现很多高考题都是源于教材,希望以此来引发学生和听课教师对回归教材的思考,让师生在备考时真正做到回归教材,聚集高考.