一道全国卷立体几何高考题的再思考

杜云龙 周长林 陈玉艳

(宁夏银川市第九中学,750011)

著名数学家波利亚在《怎样解题》一书中基于宏观思考过程对数学问题解决进行了分析,提出数学解题应为审题、计划、执行、回顾与检验四个步骤,是从现有水平出发,突破障碍,达到目标的过程,系统地阐述了数学问题解决实质上是一种既有过程又有结果的思维活动．

2017年版《普通高中数学课程标准》指出，在数学学习与应用过程中，逐步形成和发展数学运算等核心素养,数学运算不仅仅是数学学习的基本任务,更重要的是贯穿数学学习的一条逻辑思维的暗线．本文以一道2018年全国Ⅱ理20题为例,在明晰运算对象的基础上,探究多种解答策略,领会命题立意,促进学生深度学习,启发学生思维创新,实现提升学生数学运算素养．

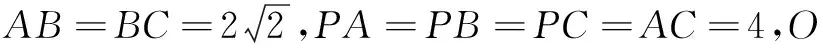
(1)证明:PO⊥平面ABC;

(2)若点M在棱BC上,且二面角M-PA-C为30°，求PC与平面PAM所成角的正弦值.

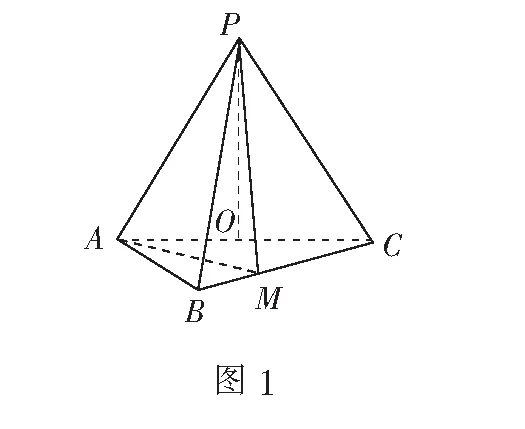
一、理解运算对象、掌握运算法则

任何问题的解答都始于对题目的理解,要解决问题，就必须从题目的叙述开始熟悉、梳理,将解答目标深深印入脑海．本题是一道符合高中数学立体几何部分考查要求的典型好题．表面上看，是考查立体几何中点线面的位置关系、空间角(线线角、线面角、二面角)的问题,命题背景简洁,但内涵丰富,具有探究性和创新性等特点．如能深度挖掘命题立意、运算对象和育人价值,将激发学生学习立体几何的兴趣,促进学生思维过程和创新意识发展．

理解运算对象的关键是分离题目的主要部分,从逐个考虑题设中的已知量和条件入手,利用图形把单个条件组合起来加以考虑,联系整个题目猜测未知量．题目以学生熟悉的三棱锥为载体,给出了三棱锥的六条棱的线段长度,如何使用六条棱的线段长度的已知条件?第(1)问要证明的是空间几何体中直线与平面垂直问题， 似乎一下子难以找到解题途径,需要进一步剖析线段的长度与点线面位置关系中隐含的背景知识，帮助寻找解题思路．要求学生通过观察数据大小,利用勾股定理判断出ΔABC与ΔAPC中的直角关系,以数解形;要求学生分析图形，厘清线线关系、线面关系,熟悉线面垂直判定定理．第(2)问是关于空间角的考查，陈述性的知识是六条棱的长度和一个二面角大小,解答本题的关键是要求学生熟悉空间角的定义以及未知点、未知线段、未知角之间内在转化,解题方法多种多样，思维将更加灵活、开放．下面以第(2)问为例进行探究．

二、探究运算思路、求得运算结果

1.坐标法

坐标法是大多数教师引导学生解决立体几何相关问题的首选方法,只需领会到建系、找点、列式、解答的一般步骤,然后套用结构,代入公式即可．影响运算的关键在于建立恰当的空间直角坐标系,准确、简洁地找到相关的未知点的坐标,以及空间向量坐标运算法则的熟练程度．

运算思路首先,以第(1)问证明的PO⊥平面ABC为基础,建立恰当的空间坐标系．如图2，以O为坐标原点建立空间直角坐标系O-xyz..

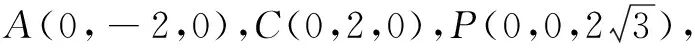
再次,利用空间向量法则列式运算．

设平面PAM的法向量为n=(x,y,z).

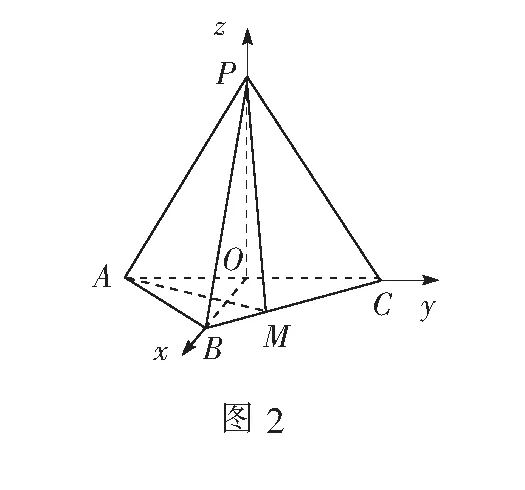
取平面PAC的一个法向量为

i=(1,0,0).

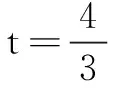
在批阅试卷时，发现大量考生的(*)步计算非常繁琐,在答题卡上解方程占了很大篇幅,致使后面书写区域不够,无法作答．造成这一现象的主要原因是学生的不良运算习惯与思维习惯．运算能力的培养不能拘泥于单纯的运算操练进行,需要结合知识点优化方法，减少运算,整体规划，养好习惯．

2.综合法

从几何视角观察和解决立体几何问题,建立空间图形与图形关系的想象力,提升学生识图作图能力,根据几何问题和图形的特点,逐步形成解决几何问题的思路．影响正确运算的关键是熟悉立体几何有关角的定义,识别与变换空间图形的空间想象能力．学生往往难以掌握,需要精心设计例题,选择几何法，强化概念的理解,明晰运算对象,增强学生的空间观念,为全面提升学生立体几何运算水平打下坚实基础．

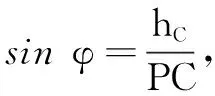
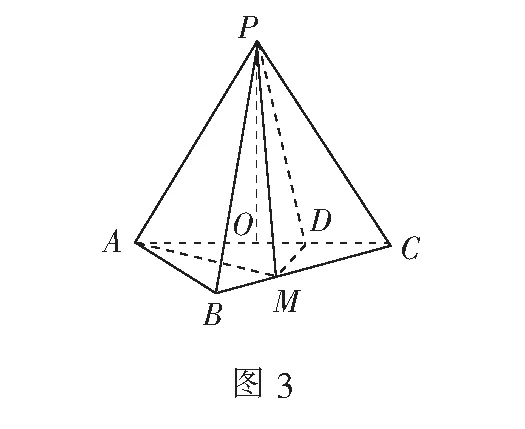
平面ABC内过点M作MD⊥AC，连结PD.因为PO⊥平面ABC，MD⊂平面ABC，由线面垂直的性质定理得MD⊥PO.

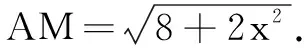
①

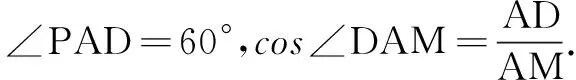
②

我们仔细观察发现，根据题目中给出的数据，无法直接计算线面角大小,如何利用二面角M-PA-C的条件?如何选择PC与平面PAM所成角的入口?如何实现条件与结论的过渡?如何寻找等量关系突破障碍?往往会用到正难则反的变通思想,根据结论推理分析后预见解题方向,再通过条件的逻辑推理、运算整理,翻译成解答过程．

三、选择运算方法、简化运算过程

前两种方法在教学中都得到强化训练、学生运算思路娴熟,但运算量较大,往往算错的概率就越大．这就需要进一步化繁为简,提升运算能力,增加思维深度,深刻理解概念,真正实现“想”得多“写”的少,促进数学思维发展．

运算思路在前面几何法中,三棱锥P-AMC中，计算顶点C到平面PAM距离的垂线长度,花费大量篇幅,如果仅仅在图形中画出来,用图说话,设而不求,则完美无瑕．

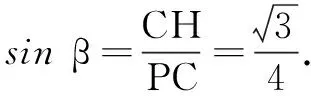
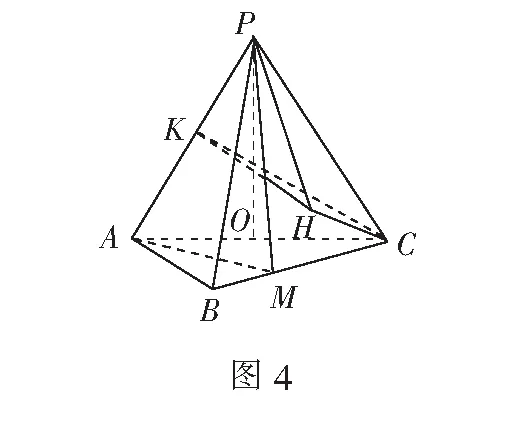
立体几何以立体图形为研究对象,所以，选择简化几何法，既体现立体几何概念本质,又培养学生空间想象能力,形成空间观念．

四、设计运算程序、形成运算机理

空间角是历年高考必考内容.这道题看似普通但不寻常,用几何的眼光观察与思考,在立体图形中看图、画图、识图、融汇贯通图中的异面直线角、二面角的平面角、线面角，方法简捷、优美．

已知二面角α-AB-β为θ，直线CD⊂α，CD与AB所成的角为φ，CD与平面β所成角的φ，则有sinφ=sinφsinθ.

结合题目直观辨析有关条件及相互关系,由表及里,螺旋上升地探究解题方法,充分揭示解题的思考过程,科学设计运算程序,不断优化解题策略,拓宽学生数学视野,使学生真正理解数学知识．

数学运算的培养具有个体差异性,不可能一蹴而就,是一个从无到有、去粗取精、日臻完善的长期过程;是通过数学好题的探究,把握数学问题解决的基本规律,学会像数学家那样“数学地思维”的思考过程;是理解运算对象,掌握运算法则,明确运算方向,设计运算程序,体现数学本质的一种思想过程．