高考第二轮复习策略研究

王 波

(江苏省常熟中学，215500)

高考第二轮复习要求是，把所有知识点梳理清楚,找到知识点之间的内在联系,把教学分成各个专题,通过专题的形式，把握重点突破难点.本文是对高考第二轮复习策略的思考，供参考.

一、不同问题抓住本质,寻求解决问题的通法

其一,专题复习除了将基本知识点上夯实外,还要注意各种知识之间的联系,强调知识的整合和知识点的统一性,通过对一些基本题目进行变式，变更条件或者结论得到问题的很多变形形式,引导学生寻求问题的本质.

例1求函数f(x)=x2-2ax+1在[-1,1]上的最小值m(a)和最大值M(a).

可改为:求函数g(x)=-x2+2ax+1在[-1,1]上的最小值m(a)和最大值M(a).

这两个问题都是求二次函数的最大、最小值,还可以改为求f(x)=x2-2x+1在[t,t+1]上的值域.这就将求动函数在定区间上的最值转化为求定函数在动区间上的最值.

这些问题都是考察二次函数的最值,是同一个问题,本质上是一样的.

其二,首先要抓住通法,在通法掌握的基础上，再进行特殊方法的讲解,以提高解题的能力.

例2已知函数f(x)=ex-x-2,k为整数,对任意正实数x,(x-k)f′(x)+x+1>0恒成立,求k的最大值?

方法二:转化为g(x)=(x-k)(ex-1)+x+1>0,对g(x)求导,讨论研究g(x)的最小值,满足最小值大于0,解出带有k的不等式问题.

这两种方法是解决恒成立问题的基本方法,必须要求掌握.但有些问题只能用其中一种方法解决,如函数f(x)=(x+1)lnx-ax+a(a>0),对于任意正实数x∈(1,+∞),f(x)≥0恒成立,求a的范围.这个问题不能用变量分离,因为涉及到函数f(x)在1处的最值不好求,必须要利用罗必塔法则,而罗必塔法则在江苏高考中又不能用,所以要选择第二种方法去做.

填空题中恒成立问题还可以用数形结合方法去研究.

最后需要对这类问题进行总结,考察了哪些知识点？主要运用了哪些方法？主要方法的一般步骤是什么？可以用哪些特殊方法去解决问题？这道题目的本质是什么？等等.

二、专题复习,知识串联,突出类比的思想

在第二轮复习时,应把知识点串联起来,并进行强化训练,检测学生掌握的知识水平,并且要加强一些新颖题的研究.比如说解析几何中有很多的问题值得研究,不同背景下表现出来的同一种问题往往会有一致的结果,通过探究会对此问题有更深刻的认识.

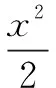
这道题目可以利用设“斜率”或者设“点”去求出BC的斜率,通过这个知识点可以串联很多的知识.

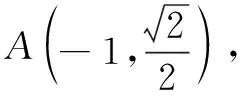
可以运用相同的方法去研究这个问题.

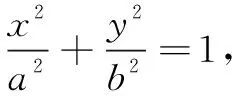
变式3如果换成圆x2+y2=a2,点A(x0,y0),求出BC直线的斜率.

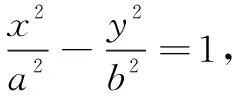
变式5如果换成抛物线y2=2px,点A(x0,y0),求BC直线的斜率.

复习时把这些问题在课堂上展现出来,通过讨论和研究,可以把整个解析几何的知识进行回顾和串联,对于基本知识的强化和提高有很大的帮助.

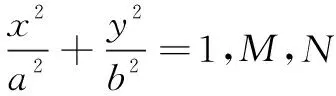
这道题的角相等也可以转化为斜率之和为零来研究.

三、突出重点,专项突破

第二轮复习时,必须要明确重点,辟为专题.如数列问题,可将其分为6个板块,第一个专题，如何顺畅求解复杂数列的求和问题；第二个专题，数列中的奇、偶项问题；第三个专题，由复杂递推关系式求解数列的通项公式问题；第四个专题，数列中整数解问题；第五个专题，数列中的恒成立和存在性问题；第六个专题，以新定义数列为背景的解答题.又如导数题,也可分为6个板块,第一个专题，导数背景下零点问题；第二个专题，利用导数处理参数范围问题；第三个专题，函数与导数中的恒成立问题；第四个专题，导数处理不等式相关问题；第五个专题，利用导数研究函数的性质；第六个专题，导数中的综合问题.而对于组合题目,可以加强数学归纳法,组合以及二项式的一些题目的练习,使得学生能够突破难点.

四、查漏补缺,注意细节

第二轮复习也是一个查漏补缺，以“错”纠错的关键阶段.将一些常见的错误让学生再进行训练,把平时做错的题目的个数标注,每隔一至两周将错题整理成一张试卷,让学生自主练习,在查漏补缺中学生可以进行反思.例如,在数列中已知Sn求an,往往漏掉n=1的情形,忽视了部分数列an的通项是分段的数列;等比数列求和时,往往漏掉公比q=1的情形.有关直线问题往往漏掉斜率k不存在的情形；还有联立直线与圆锥曲线时忘记Δ>0这个解集.再比如研究f(x)=x3+3x2+3x的极值点,对函数求导f′(x)=3x2+6x+3=0,得到x=-1,实际上通过列表发现在x=-1两侧的单调性都是增函数,所以函数f(x)无极值点. 上述在细节上出现的问题可能是粗心，也可能是掌握不牢固,要求学生根据自己的情况对症下药,在模拟考试和高考中,通过自己集中精力做题,通过自己的意志力克服这些困难.

总之,第二轮复习在高三数学教学中有非常重要的作用,可以把第一轮复习的基本知识通过专题进行重现,打通了基本知识之间的联系,并且在基本知识的基础上进行提升.另外，在第二轮复习中,还可特别加强一题多解的练习,对同一个问题运用函数、向量、或者解析几何的建系方法等进行解答；还有对多题一解的专项训练,对同一类问题用统一的消元或者建系的方法进行求解；以及对类比的思想的渗透,比如对三种圆锥曲线的结论进行统一的比较和分析.