数学抽象素养视角下的“支架式”教学——以“椭圆及其标准方程”的教学为例

刘润慧

(西北师范大学教育学院,730070)

本文以《普通高中课程标准实验教科书·数学》(人教A版)选修2-1,第2章第2节“椭圆及其标准方程”为例,探析基于支架式教学模式培养学生数学抽象素养的一般策略，旨在为一线教师的课堂教学提供参考,更好地落实核心素养培养的目的.

一、数学抽象及支架式教学理论的相关介绍

数学抽象作为数学重要的基本思想,是通过学习而形成的适应个人终身发展和社会发展需要的必备品格和关键能力[1].数学抽象是数学的基本素养,是形成理性思维的重要基础,反映数学的本质,贯穿在数学产生、发展、应用过程中[2].史宁中老师在《数学思想概论》中提到,数学抽象依照其深度差异可分为三个阶段:简约阶段、符号阶段、普适阶段[3].高中生经过义务教育阶段的发展,思维水平早已跨越第一层次,因此,高中阶段的数学教学要以学生现有的知识基础和思维发展水平为着力点,合理设计教学,采用恰当的教学方法,启发学生思维,逐步引导学生进行学习,从而提高自身的抽象素养.

支架式教学是基于建构主义学习理论为基础提出的教学模式,它通过调动各环境要素为学生搭建合适的教学支架,通过分层分段的教学体系将知识或任务呈现给学生,使学生形成对新知的建构,旨在培养学生的问题解决能力和自主学习能力,从而达到素养提升的目的.支架式教学分为五个具体环节:创设情境、搭建支架、独立探索、合作学习、效果评价[4].

探究抽象素养视角下支架式教学模式在课堂中的具体应用,即通过设置一定的情境中,搭建与学生当前认知水平相适应的教学支架,引导学生在支架的搭建与撤销中,主动思考、合作探索,完成对新知识的学习,接着再针对整个学习过程进行综合评价,最终使学生达到知识和素养的双重提升[4].

二、支架式教学模式下“椭圆及其标准方程”的教学设计探究

1.支架式教学设计理念分析

在学习“椭圆及其标准方程”内容之前,学生已经初步学习了用坐标法研究几何问题的一般思路,并掌握了求曲线方程的方法.通过椭圆概念的探究过程,使学生学会从具体实例中提炼数学概念的方法;通过椭圆标准方程的推导,让学生熟练掌握求动点轨迹方程的方法——坐标法.由“椭圆及其标准方程”的教学,探析支架式教学发展学生数学抽象素养的一般策略.在教学过程中，要特别注重发挥学生的主体地位,促进学生探究意识、合作意识的培养,并在教学支架的搭建与撤销过程中,逐步发展学生的数学抽象素养.

2.“椭圆及其标准方程”支架式教学的具体实施路径

(1)新课引入

教师利用多媒体向学生展示一则卫星成功发射的新闻,接着教师引导学生观察卫星的运行轨迹,引出椭圆.教师继续引导学生发现生活中的其它椭圆现象,使学生感知,椭圆在我们日常生活中的普遍存在,从而引出本节课将要学习的内容“椭圆及其标准方程”.

评注教师以我国北斗卫星顺利发射为背景,搭建情感支架,唤起学生强烈的民族自豪感,从而激发学生求知欲.

(2)新知探究

① 椭圆概念的探究

支架1教师提问:“椭圆在生活中十分常见,那么如何在一个平面上作一个椭圆呢?”

活动1教师提示在黑板或桌面的硬纸板上，用图钉固定绳子的两端,并要求绳子的长度要大于两图钉间的距离,接着套上铅笔,使绳子保持拉紧状态,移动笔尖,画出相应的轨迹.

通过以上操作,结合圆的定义,学生通过小组合作,讨论交流,得到如下定义：“平面内与两个定点的距离的和等于定常数的点的轨迹叫做椭圆.”

支架2思考该定义是否完整?还需要补充哪些内容?

活动2学生进行小组讨论,给出以下的补充内容：第一,两定点与动点必须在同一平面上;第二,必须强调动点到两定点的距离之和大于两定点之间的距离.

支架3通过上述活动,椭圆的定义得到初步完善.思考:如果给定线段长度和两个不动点位置,是否可以生成椭圆?如果可以生成,有哪些限制?

活动3教师在黑板演示,定点为A、B,动点为C有哪些可能存在的情况?学生动手实验,小组讨论，归纳结论.根据我们动手实验及老师的演示以及讨论,同学们得到如下结论：(i)当|AC|+|BC|>|AB|时,轨迹是椭圆.(ii)当|AC|+|BC|=|AB|时,轨迹是一条以AB为端点的线段.(iii)当|AC|+|BC|<|AB|时,无法构成图像,无轨迹.

评注教师基于学生的讨论,分别用文字语言和集合语言对椭圆定义加以描述,进一步完善椭圆定义.至此,椭圆完整的定义就在学生自主探索合作交流中完成了,在该过程中教师通过搭建不同层次的教学支架,引导学生观察、思考、讨论,最后总结出椭圆的定义.学生作为学习的主体,全程参与概念的探究过程,加深对于概念形成的理解,提高概括能力和动手操作能力,在活动中提升数学抽象素养.

② 椭圆标准方程的推导探究

支架4基于用坐标法求动点的曲线方程,椭圆的轨迹方程如何推导?

教师和学生一起复习用坐标法求动点轨迹方程的一般步骤,接着通过搭建问题支架4和5,推导椭圆的标准方程.

活动4学生独立思考、合作交流“建立直角坐标系”，学生通过交流,归纳出建立两种建立直角坐标系的方法,接着以不同的建系方式推导相应椭圆的标准方程.

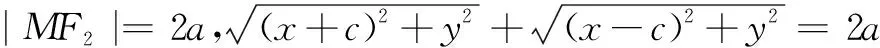
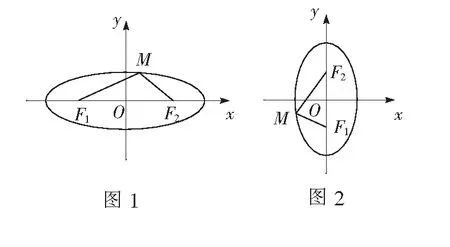
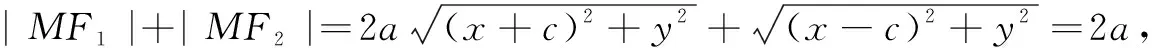
支架5教师引导学生小组合作,归纳焦点在x轴和y轴上椭圆标准方程的特点?

活动5学生独立思考后与小组成员讨论,焦点不同的椭圆的标准方程及其特点.讨论结果，如表1.

表1 椭圆标准方程及其特点的归纳

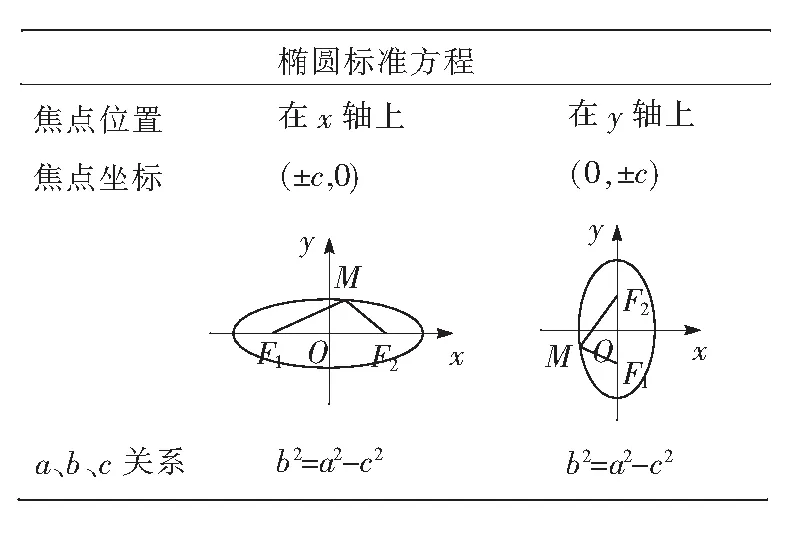
(3)巩固应用

教师通过多媒体展示相关习题,学生先独立完成,接着小组讨论,最后教师对学生学习结果做出评价.通过相关题型的巩固,达到对知识更加深入理解与掌握的目的.

(4)课堂小结

评注学生在教师的引导下,亲身经历了“问题支架——独立思考——合作交流——结果评价”的多次循环的探究过程,实现较高层次的思维启迪,从而达到发展学生数学抽象素养的目的.

学生通过自身体验、动手实践,在支架的搭建与撤销中,完成了椭圆概念及其标准方程的探索,既掌握了求曲线方程的方法,又在一定程度上提高了概括能力,发展了数学抽象素养

三、支架式教学模式下培养学生数学抽象素养的路径分析

应用支架式教学发展学生的数学抽象素养,既要分析教材的内容结构进、厘清重难点,又要考虑学生现有的知识水平,构建科学合理的教学支架.

1.搭建与认知水平相适应的教学支架

教师在设计教学支架时,要以学生作为主要参考对象,根据学生知识基础和认知水平,遵循由易到难、循序渐进、螺旋上升的原则搭建教学支架[5].通过搭建支架,引导学生自主探究、合作学习,在数学活动中,经历知识的建构,逐步发展数学抽象素养.

2.搭建与抽象层次相适应的教学支架

学生的数学抽象素养必须在数学抽象的过程中培养,而数学抽象的过程又具有层次性,因此在搭建教学支架时要与学生的抽象层次相一致.高中生经过九年义务教育,其思维的抽象水平早已跨过了抽象的第一层次“简约阶段”,到达了抽象的第二层次“符号阶段”.在这一阶段,强调去除具体内容支撑,利用数学符号描述数与形之间的关系.如上述椭圆的标准方程的推导,就是用符号语言描述椭圆曲线所对应的标准方程,这是抽象的第二层次在教学中的体现.

3.搭建与数学抽象素养长期性和潜在性相关的教学支架

需要注意,数学抽象素养的培养是多方面的,也是一个长期的过程,它的形成与发展不是一蹴而就的,需要长期潜移默化的熏陶[6].因此,我们在利用支架式教学进行教学实践时,要考虑到数学抽象素养形成的潜在性和长期性,立足当下,搭建与学生自身发展相适应的教学支架,为后续抽象素养的继续发展奠定基础.

总之,数学抽象素养是在数学抽象过程中逐渐积累核心素养,是适应个人终生发展和社会发展需要的必备品格和关键能力.支架式教学则是以学生为主体,通过搭建螺旋上升的教学支架,在自主探索、合作交流中,逐渐形成对新知的系统建构,进而达到对知识灵活运用的目的.支架式教学模式是发展学生数学抽象素养的一个有力工具.