差异教学下同题异构课教学策略分析*

林建森

(福建省石狮市石光中学，362700)

同题异构课教学是为了适应新课改而提出的一种新型的教学方式,其中同课是基础和前提,异构是发展和延伸．其特点是，同样的教学内容,因为教学经验等不同，就使得教学设计存在一定差异．如何有效地实现差异教学？本文对同题异构课的教学策略进行探讨.

一、设计有效的课前导入,激发学生学习兴趣

好的开始是成功的一半.精彩的导入，在一开始上课的时候就能够吸引学生的注意力,让学生对本节课产生浓厚的兴趣．

案例1人教A版高中数学必修1的“集合的含义与表示”是高中数学的第一节课,所以其课堂教学的好坏将会直接影响到整个高中数学的学习．通常，教师在进行课堂导入时，都会引用学生以前接触过的有关集合的概念,如有理数的集合，自然数的集合，圆的概念(到一个定点的距离与定长相等的所有点的集合)，或者是不等式x-8<4的解的集合等等，最后通过这些实例引出集合的概念,也就是将有关研究对象称为元素,这些元素的组成总体就是集合．其实，教师可以在上课之前，向学生展示一些他们比较熟悉的生活情境.比如可以利用学生在开学时的军训活动,提问学生，通知学生参加军训的对象是高一学生还是个别学生？然后学生回答，这样可以有效缓解第一节数学课上课的紧张感.接下来教师根据学生的回答做出总结,告知学生，集合是经常会用到的一个概念,其研究的对象并不是个别,而是总体．由此引入集合的概念,这样的引入方式会在最大程度上吸引学生的注意力,还能够激发学生进一步探究的欲望,在课程一开始就调动起来学生学习的积极性,同时也逐步培养学生的数学抽象核心素养．

二、设置疑问进行探究,提升学生学习能力

新的教学理念强调在教学时要着重培养学生的自主学习能力,充分尊重学生的主体地位.在课堂教学过程中，巧妙地设置一些问题，使学生能够自主探究,发散思维．

案例2针对人教A版高中数学必修1的“集合的含义与表示”一课来说,通常教师都会在上课时列举一些和集合有关的例子,让学生思考和探讨集合中各个元素之间所具有的共同特征,以及集合的构成要素是什么等等．然后就会直接进行讲述,用大写字母A，B，C，…表示集合;用小写字母a,b,c，…表示集合中的元素.若a是集合A中的元素,则称a属于集合A等．如果教师在讲授集合与元素时使用这道题来引导学生,即判断下列元素的全体是否可以组成集合?

(1)我校2018级新生；

(2)大于5且小于13的奇数；

(3)x2+1=0的解；

(4)世界上的河流数量；

(5)非负偶数.

如此导入，可以让学生总结出集合中元素的主要特点,这种直接导入的方式，更加直观和利于理解,能够促进学生自主学习能力的发展,同时也可逐步培养学生的直观想象与数学抽象核心素养．

三、进行课堂延伸,巩固所学内容

在基本教学内容完成之后，为了检验学生是否将知识内容掌握牢固，最好的一个检验方式就是在课堂中将相应的知识点进行延伸,比如可以布置相应的练习，让学生写具体的学习感受,或者直接设计问题等．

案例3设计“集合的含义与表示”的课堂练习(或课后练习)

1.下列选项中元素的全体可以组成集合的是( )

(A)学校篮球水平较高的学生

(B)校园中长得高大的树木

(C)小于19的所有自然数

(D)中国经济发达的城市

2.下列判断正确的是( )

3.方程x2-1=0的解集是( )

(A){1} (B){-1}

(C)1,-1 (D){1,-1}

4.已知集合M={a,a2},则实数a不能取到的值为______.

5.已知方程x2-3x+a=0的解集中的一个元素为1,则实数a和该方程的解集为______.

6.已知方程x2-2x+2a=0的解集中没有实数元素,求实数a的取值范围.

7.已知方程x2+ax+b=0.

(1)若方程的解集只有一个元素,求实数a,b满足的关系式;

(2)若方程的解集有两个元素分别为1,3,求实数a,b的值.

由于这部分教学内容中的概念相对比较抽象,所以学生对其理解与掌握都有一定的难度.因此,教师可以给学生设置以上问题,使其能够在练习的时候掌握教学内容,以此给后续数学的学习打下坚实的基础，并通过问题的练习巩固,逐步提升发展学生的数学运算、逻辑推理等核心素养．

四、充分尊重学生在课堂上的主体地位

对于教师而言，不管是在怎样的情境之中，都应该要给予学生主体地位充分的尊重.例如在充分沟通与交流的基础上,引导学生发现并探索知识,促使他们积极主动地去学习．例如，在解析函数问题的时候,有些教师在进行简单的讲解之后，就让学生使用不同的方式去进行解题．如果把学生划分成若干个小组，让其针对问题进行讨论,再对学生讨论中使用的不同方式进行点评,给学生的解题思路予以确定,把存在的问题及时纠正和处理,可帮助其养成一题多解的学习习惯和解题思路．

案例4使用配凑法求某复合函数f[f(x)]中f(x)的解析式．其中f[f(x)]的表达式一般会将其配成g(x)的运算形式．应该注意的是，所要求得的函数的定义域并不是原先复合函数本身的定义域,而是g(x)的值域．

例1已知f(x-1)=x2-2x求f(x)和f(x+2).

解因为f(x-1)=x2-2x=(x-1)2-1,所以f(x)=x2-1.

故f(x+2)=(x+2)2-1=x2+4x+3.

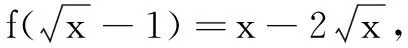
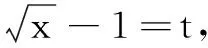
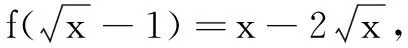
所以f(t)=(t+1)2-2(t+1)=t2-1，

所以f(x)=x2-1，其中x≥-1.

故f(x+2)=(x+2)2-1=x2+4x+3,其中x≥-3.

以上几个方式的具体选择，应该要以学生的实际学习情况为基础,要确保学生能够对函数产生充分的认识,并且学会使用不同的求解方式解题,达到提升数学学习能力,培养学生的数学抽象、数学建模核心素养的目的．需要注意的是，教师还应该在同题异构教学方式下，与学生多交流,多了解学生的解题思路及学习进度,同时要做好相应课程内容的准备,保证教学的有效性．

综上可知，同题异构课教学是否完善？差异化的教学是否能够获得良好的教学效果？都是需要教师合理地整合课堂教学的内容,保证教学方式的有效实施．所以,只有将数学教师在差异教学之下对同题异构课教学的认识提升上去,对同题异构的课程内容进行充分研究准备,才能够有效促进其具体教学方式的实施,才能够保证学生的数学学习质量,提高数学学习效率和综合能力,进而逐步提升学生的数学核心素养．