高一新生数学学习障碍的成因研究

张 兵 李祥金

(江苏省丰县民族中学，221700)

学习障碍或学习困难，又称特殊学习需要,是指尽管智商没有问题,也没有发展迟缓,但在听力、会说能力、阅读能力、书写能力、计算能力、推理和推论能力这些特殊领域的学习或使用上却出现问题,而引起的学习困难．因此,高一学生数学学习障碍主要表现是，学生在数学阅读、计算能力、推理与推论这些领域的学习上，没有跟上高中学习的要求，而出现暂时的困难．由于从初中到高中，学生的学习环境变化、学习强度、学习方式等不同,使学生产生学习困难的原因也是多方面的.此外,高一数学老师大都是刚从高三任教轮换过来的,他们的教学方式短时间内还不能适应高一学生的认知水平,这也是造成学生学习困难的原因之一．

从学习个体的角度来说,高一学生处在人生发展的过渡时期,他们的身体素质与心理素质进一步成熟,认知能力与思维能力,处在快速的提升阶段,但这些因素也具有一定的不稳定性．例如在数学学习上,虽然经过初中阶段的学习,他们的认知能力与思维能力得到了较大提升,但是由于高中数学学习难度大、学习内容较多,而且对学生的思维能力,逻辑推理能力比初中要求高；同时，刚进入高中的数学内容主要以函数知识为主,其信息量大，应用广泛，计算能力要求高，解决问题的方法多样,这些都是造成许多学生在高一阶段学习数学感到“力不从心”,对学习数学不适应,数学成绩一落千丈的重要原因.因此,研究影响学生困难的各种因素,找出解决这些问题的相应对策，是降低学生在高一阶段学习困难的有效策略．笔者认为，造成高一新生学习障碍的因素主要有以下几个方面.

一、初、高中学生学习方式的不同

初中阶段，由于学生的学习知识点少、难度较低,对数学的逻辑思维要求较低,因此,数学老师可以对难点反复讲解,课内、课外对这一难点进行反复的、机械性的训练,即对数学的要求以记忆、重复为主;高中阶段由于学习内容比初中阶段要多,难度也大,并且面临高考升学的压力,教师不可能按照初中的教学行为组织教学,这不但要求学生记忆,更需要学生对问题的理解.许多学生由于在初中长期形成的学习行为的影响而不能适应高中阶段学习数学的要求,造成学生在学习中感到不适,从而造成两极分化．

学习行为的形成不是一朝一夕就能得到的.因此,要改变学生的学习行为，并不是短期能够完成的,这需要老师对学习行为出现问题的学生要有足够的耐心，帮助他们进行学习习惯的改变．具体地，可考虑从以下几个方面着手组织教学.

(1)引导学生学会听课．学生会听课并不仅仅指学生课堂上专心听讲，把老师的话都记在心里,而是老师根据研究的问题引导学生发现问题、分析问题、解决问题,应允许学生对问题进行争执、讨论．学生在这种争论中，除了对知识的正确认识外,更主要的是有利于学生智力的发展,思维水平的提高．

(2)引导学生学会小结．引导学生进行学习总结，也是培养学生形成好的学习习惯的重要方法．小结的类型主要有两种:一种是对知识的理解．当学习完一个章节后,教师应引导学生对本章的内容进行回忆性总结,包括本章所涉及的概念、定理、推论及解决本章内容的基本方法、思想等．另一种为解题思路的总结．主要总结解决具体问题时不同的方法,在解决问题的过程中研究解决问题所涉及的基本思想、基本方法,进一步寻求解决问题的最佳方案．

通过学生的独立思考与小结，不仅可弄清概念、公理、公式的来龙去脉,发掘知识的内涵,更重要的是培养学生独立思考、善于总结的良好学习行为,为培养学生的数学素养奠定基础．

二、初高中教材编排的衔接不畅

高中数学知识与初中知识相比，具有更强的系统性与逻辑性,要求学生也应具有更强的理性思维.反观最近几年的初中教材,经过几次的调整,更注重学生的感性思维．因此,许多知识是高中学生解决数学问题必备的知识,但在初中阶段仅作为阅读材料,例如根与系数的关系；或者干脆忽略不讲,例如因式分解中的“十字相乘法”、绝对值不等式的解法等等，而这部分知识高中教材又没有涉及，造成衔接不畅.由于上面这些原因，造成一部分学生在进入高中学习阶段感觉比较困难,逐渐失去学习数学的兴趣与动力．

教学应遵从知识的发展规律和学生的认识规律．为了使学生进入高中阶段尽快适应高中数学的学习,尽可能地解决学生因初高中知识的衔接而造成的学习困难,在前期,教师可以根据实际情况，补充一些学习高中内容必备的知识,例如一元二次方程根的判别式、根与系数的关系、二次函数的图象与性质,十字相乘法、立方与差的公式、最值等，使学生尽快适应高中数学的学习．

三、数形结合的意识不强

虽然在初中阶段学生已经学习了函数图象的画法,在实际教学中,笔者却发现，许多学生对函数的解析式与相对应的图象并不能很好地理解,对稍微复杂的图象不能正确画出,甚至有些学生不知道y轴方程式为x=0,或者不理解x≥1在平面坐标系中所表示的区域．初中阶段,老师往往是让学生看到解析式马上想到函数的相应性质,或者是给出函数的图象解决问题,而通过自己动手画出函数图象解决问题的能力非常弱.高中阶段往往涉及根据函数解析式,自己画出图象,再利用数形结合的手段解决问题,造成许多学生不适应高中教学的要求,从而感到高中数学比较困难．把数形结合起来,用代数的方法分析题型,用图形来直观理解数、式的关系，是高中生必备的数学技能．为了使新入高中的学生尽快适应高中的教学要求,教学中,老师引导学生在已学过的基本图形的基础上作图,了解平移变换、周期变换、翻折变换等,培养数形结合的意识；并理解各种式子的几何意义,使学生对数学从数、式和几何图形等方面理解数学,有利于学生数学素养的形成.此外,教学过程中老师也可通过几何图形组织教学,降低数学的抽象性．

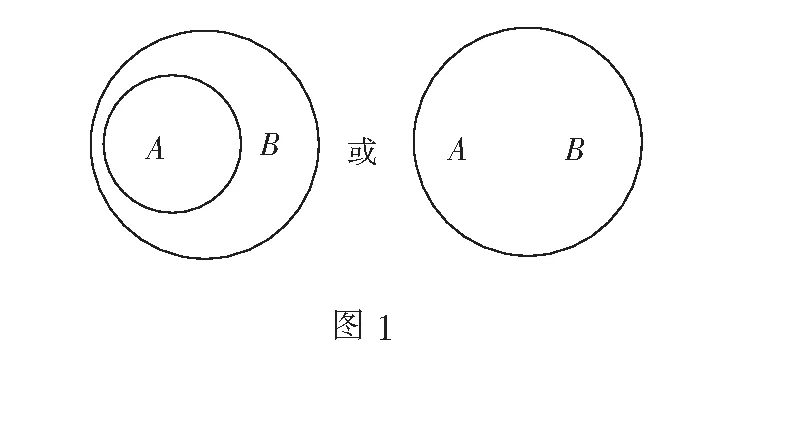
例如，集合子集的概念(苏教版必修一):如果集合A的任意一个元素是集合B的元素(a∈A,则a∈B),那么集合A称为集合B的子集,记为A⊆B或B⊇A,读作“集合A包含于集合B”或“集合B包含集合A”．教学中,任意a∈A,则a∈B,可以借助图形帮助理解A与B的关系(图1)．

四、数学符号意识不强不能适应高中教学的要求

斯托利亚尔认为:“数学学习就是数学语言的学习”．数学发展的历程实质上是数学符号发展的历程．由于心理、知识层次等多方面的影响,初中阶段学生善于利用文字语言表述问题．例如高中阶段单调增函数的概念表述为:设函数y=f(x)的定义域为A,区间I⊆A．如果对于区间I内的任意两个值x1,x2,当x1

例如，在函数概念的教学中,有两道求函数定义域的题目:

(1)已知函数f(x)定义域是[0,2],求函数f(x2)的定义域．

(2)已知函数f(2x+7)定义域是[-2,5],求函数f(x)定义域．

由于学生对于对应法则f所表示的意义理解不透,造成学生对老师讲过的试题会做,而对没讲过的却束手无策的状况． 为了有效帮助学生对数学符号表示的含义理解及数学语言之间的转化,下面几种方法可以尝试应用：(1)帮助学生利用已有的经验尝试解读数学符号；(2)通过用数学符号语言表达自己的想法；(3)老师要用自己的语言规范学生的表述；(4)从数学符号含义本身去讲解．

陶行知先生说过，创造始于问题,有了问题才会思考，有了思考才有解决问题的方法,才能找到独立思路的可能．高一年级是整个高中阶段打基础的重要一年,是学生以感性思维思考问题为主向以理性思维思考问题为主转变的重要节点,也是学生适应高中教学的初始阶段.为了有效降低学生两极分化,教学中,老师应在实际的教学中勤于观察出现的问题,及时调整教学行为，或者根据学生的个体差异因材施教等策略,使大部分学生都能跟上自己的教学,有利于学生的数学素养的形成．