初中数学应用问题中渗透数学建模思想的策略研究

巩玉英 田承恩

摘要：“数学建模”是解决中学数学应用问题的常见方法，其主要是指利用抽象思维、简化手段、假设条件和变量关系引进等数学解题思维，用数学方式对数学实际问题进行表达，通过模型方法求解的解題方式。本文重点针对初中数学应用问题中渗透数学建模思想的策略展开研究，并以“鲁教版”初中数学为例，笔者结合相关实例提出自己的思考与启发，希望通过以图建模，培养学生的审题能力；通过类比转化建模，培养学生的应用意识；针对“最近发展区”建模，促进学生思维的发展，有效激发学生学习兴趣，提高分析问题和解决问题的能力，提升初中数学教学成效。

关键词：初中数学；应用问题；数学建模思想

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）11-0155

核心素养教育视角下，初中数学课堂教学也应因时而变、因材施教，尤其对于正处于初中阶段的学生而言，在数学教学中更要有意识地激发和培育学生的学习意识，因此教师在课堂教学时的侧重点不应只是过度关注学生的数学学习成绩，而是通过对数学建模思想的有效渗透和应用，鼓励学生在中学数学学习中有效应用建模思想，借助数学模型有效解决数学问题，培养数学思维意识，提高学习效能。正如著名数学家怀特海曾说：“数学就是对于模式的研究和运用。”诚然，数学建模思想是贯穿于初中数学、高中数学乃至高等数学教学中的一种重要学习思维和方法，在数学建模教学中，教师要多引导学生学数学、做数学以及用数学，这对于提高学生数学成绩，培养学生创新思维意识，引导学生由“应试教育”转向“素质教育”具有重要意义。

一、以图建模，培养学生审题能力

在初中数学教材中应用问题较多，其中包含了很多数学信息，而题干涉及的文字也繁多，这在无形为对学生的信息筛选能力和题干信息的阅读和理解能力增加了很多困难。对于一些相对复杂的数学应用题，学生需要对相关隐含信息内容进行转换，并将其转化为数量关系、数学符号或已知的数学变量，因此建立数学模型尤为重要。学生在解决这类数学应用问题时，可通过图标建模在图表或图形中获取相关的解题数据信息，也可借助数学图表、相关数学图形等转化变量之间的关系，结合数量关系列等式。这样一方面能够有效培养学生的审题能力，另一方面还可增强学生对相关数学问题已知、未知数据的处理能力。

例如，在讲解初中数学中的行程应用问题时，教师可通过画线段的方式引导学生根据图形找数量关系。如甲、乙二人同时从相距18公里的西村和东村出发，已知甲每小时行走14公里，并在2h后可以追上乙，那么请问乙每小时行走多少公里？对于这类题型，先假设乙每小时行走x公里，然后可以图建模：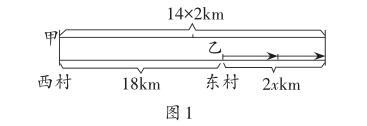

根据图1中数学模型，即可得到等式关系：18+2x=28，x即等于6公里。

二、类比转化建模，培养学生应用意识

与其他学科相比，数学与学生的日常生活实际联系最为紧密，而在初中数学应用问题教学实践过程中，关键和重点是要培养学生的应用意识，即通过分析问题和解决问题培养学生“用数学”的意识，使其自然而然地学会将数学知识与日常生活实际相联系。但有些初中数学知识点复杂，无法直接建立模型，针对此类应用问题需要引导学生多角度思考，培养学生的数学思想、数学精神以及数学处理方法，通过类比转化建模，让学生学会在数学解题过程中学以致用。

例如，在一元一次方程的教学过程中，有如下应用问题：A和B每天晚上在学校的环形跑道中跑步锻炼身体，已知该环形跑道的长度为400米，其中，A和B平均每秒钟分别跑5m和7.5m。有一天晚上，B对A说：“我比你速度快，这次你可以先跑25m，然后我们再一同开始跑。”那么请问：1. A和B同时同向出发，两人需要多长时间才能相遇？2.在2点和3点之间，若时针和分针重合，此时会是什么时刻？3.在2点和3点之间，请问时针和分针若要成直角或平角，需在什么时刻？

此类数学应用题考查的是学生对一元一次方程的应用及数学变式关系的应用，而在初中数学中，这两种基本问题可以实现类比转化，只要引导学生建立如下图所示的数学模型，即可让学生更加直观地找出题目中所隐含的数学等量关系，也可直接将钟表中的数学问题转化为生活中的追击问题，这种解题思路难度适中，更加贴近学生的日常生活实际，通过建模解题可增强学生的自信心，帮助学生树立数学思维意识，使其在解题中由被动变主动，有效激发学生的学习兴趣。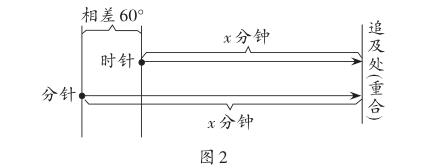

三、针对“最近发展区”建模，促进学生思维发展

近年来，在新课改背景下，初中数学教学更加强调对学生核心素养能力的培养，尤其是初中数学，其知识点多、内容繁杂，学生理解起来相对比较困难。以初中数学应用问题的教学为例，教师通过数学建模，即可通过解题方法创新，针对“最近发展区”建模，培养学生的数学思想，创新解题意识。

比如，某工厂有22名工人生产螺母和螺钉，其中每个工人每天平均可以生产2000个螺母和1200个螺钉，已知1螺钉可配2螺母，为了使螺钉和螺母正好完全配套，请问该工厂每天至少应该分配多少名工人生产螺钉和螺母？

很显然，此类问题也属于应用型数学题，数学题干内容来源于学生的日常实际，所以在解决这类数学问题时，教师要打破常规，不能盲从课本知识，寻找学生的“最近发展区”，根据学生兴趣建立数学模型，让学生联系实际，引导学生列表格、画示意图等对相关数学问题关系进行表征，根据不同类型的应用题，建立不同的数学模型。在此题中，可让学生假设该工厂每天生产螺钉至少需要x人，由此可根据上述已知题意列出如下表格模型。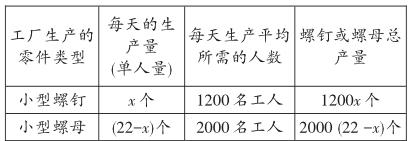

通过上述图表建模方法，可启发和引导学生多去深入思考与题目内容相关的概念、条件或结论等，以图表建模优化数学应用问题解题策略。

对于初中学生而言，在自主探究与实践中能够激发学生学习数学的兴趣，在体验中加深对知识的印象，从而获得学习的成就感。尤其是在初中数学教材中，应用问题包含数学信息文字繁多，无形中会对学生阅读和理解能力产生影响。但毋庸置疑，数学是一门与学生日常生活联系最为紧密的基础學科，其更加强调学生的综合学习能力与数学逻辑思维。而数学建模思想是一种有效的解题策略，建模的本质与核心在于引导学生掌握数学知识学习方法和数学应用题解题技巧，通过不同方式建立合适的数学模型，有助于培养学生的想象力、观察力和创新创造能力，塑造学生的核心素养。因此，在初中数学应用问题的教学中，教师的根本任务就是要有意识地培养学生的建模思维能力，通过分析、解决问题引导学生善于“用数学”，并自然而然地学会转化数学问题。只有积极改变策略，践行新课改教育指导精神，更加注重对学生核心素养能力的培养，才能指导学生通过数学建模和解题方法创新培养数学思想，创新解题意识。

通过以上案例分析及论述可以看出，数学建模能力的培养不是一蹴而就，应在平时点点滴滴的学习中进行长期的渗透和积累。因此，在教学实践过程中，教师要善于对学生学习技能进行培养，积极转变教学方法和思路，引导学生在数学学习过程中，多从生活实际出发，多观察和总结身边的数学，将实际问题与数学问题相结合，在解决数学问题时，要从多角度入手，学会运用数学模型分析问题与思考问题，借助数学模型将具体问题简单化，真正提高解题能力，激发学生学习数学的乐趣，促进学生多方面数学能力的提升，使学生可以学习和运用有用的数学知识，产生巨大效益，并使学生终身受益。

参考文献：

[1]张建鹏.在中学进行数学建模教学的体会[J].重庆教育学院学报，2010（3）：116-118.

[2]莫友明.加强初中数学建模教学培养学生应用数学意识[J].当代教育论坛（教学研究），2011（6）：72-74.

[3]李倩倩，陈志强，韦程东.在初中数学教学中融入数学建模思想的浅析[J].广西师范学院学报（自然科学版），2011（S1）：119-122.

（作者单位：山东省淄博市桓台县城南学校256400）