数学建模的思想和方法的应用
2016-10-14郭胜红
郭胜红
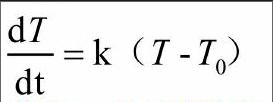

摘 要:本文中,笔者首先结合我国高数教学现状,分析了建模思想在高等数学教学中的重要性,并且阐述了数学建模思想应用到教学中应遵循的相关原则,并结合具体问题探究建模思想的应用价值,以其能够产生一定的实际意义。
关键词:数学建模思想;高等数学;教学原则;重要性
前言:众所周知,高等数学是高校理工科学生重要的必修课之一,而且高数这一学科往往抽象性强、理论程度深、数学规律和定律较多,在教学时比较枯燥乏味,致使学生学习的积极性不高。并且很多学生认为,高等数学是一门“无用”的课程,生活中难以让高等数学产生一定的实用价值。作为高等数学教学及解题过程中的重要思想和方法,数学建模思想对于高效的解决各类复杂的数学问题至关重要。常见的微积分、导数等数学概念往往都比较抽象,运用建模思想则可以让其具象化。在解决实际数学问题的应用过程中,建模思想的作用更加突出。
一、建模思想在高等数学教学中的重要性
建模,顾名思义就是建立模型,在高等数学教学过程中,建模的过程往往是对一个具体的对象,为了达到某种目的,遵照其内外规律,对复杂的数学结构做出进一步的简化,提出假设,并利用合理的数学工具或者公式,通过正确的运算,来构建成为一种数学模型结构。简单的说,建模就是通过数学公式或者图形等数学语言来对数学问题和现象进行的描述。随着高校高数教育教学的发展,高数建模思想也在不断发展。但是从实际情况来看,我国高数教学创新理念不高,教学方式单一,枯燥无聊的数学课堂让学生们提不起兴趣,最终影响了学生思维的灵活性和个性化成长。因此,新时期的高数教学中,需要不断增加和融入了数学建模思想,对于学生思维活性和数学创新能力的发挥作用明显。学生在数学教师的引导下,积极进行数学创新,并主动发现、分析和处理相应的实际问题,大大提高了高等数学的教学效率和质量水平。建模思想对于高等数学整体教学水平的提升具有深远的意义。
二、数学建模思想应用到教学中应遵循的原则
1.实例要简明易懂
在实际的数学教学过程中,虽然模型建立至关重要,但是对于模型实例来讲,应当是简明易懂的。由于数学学习具有较强的理论性、规律性和逻辑性,甚至有些定理比较晦涩,因此教师应当积极借助相关的生活实例来展开教学,简明的生活实例能够帮助学生深入浅出的进行学习,激发学生们对数学的学习热情,循序渐进的引导学生从实际问题分析入手,探究其中的数学内涵与奥妙,并深刻理解和掌握知识。尤其是对于微积分和该类方面,教师要深化学生的学习理念,提高学生的建模意识,引导学生认识到数学学习的重要性,并展开深入的学习。
2.坚持因材施教
任何学科的教学都应当注重因材施教,针对学生特点进行个性化的、有针对性的教育,而且由于各个学校教学都有其自身特征,对于理工科专业和文史专业而言,高数教学的模式和方法应当是有所差异的。为了提高数学建模思想在教学中的应用,高数教学应当做到因材施教,提高教学的实效性,并在教学过程中积极开展科研工作,不断发现、分析、处理和解决问题,提高教学质量。
3.教师应编写可以融入的教学单元
在互联网发展的今天,教师可以借助互联网资源或技术,积极分析高数课程教学实际问题,并建立和挖掘数学建模的素材,对高数教学从问题陈述、建模、求解、验证等过程进行研究与思考,并将其与现有的教学单元有效融入,帮助教师进行教学与科研,进而提升单元教学水平,促进教师教学风格的塑造与教学水准的提高。
4.对新生要进行重点教学
对于新入学的学生,即大一秋学期的学生应当积极开展数学建模思想意识强化,帮助学生建立并形成数学建模的正确思维模式,由易到难的引导学生利用建模实现对实际问题进行分析与探究,引导学生理解高数对生活的重要作用,并结合一定的理念强化和理论知识灌输,让学生认识到建模思维在数学学习中的重要性。
三、建模思想在高等数学教学中的应用
1.在概念教学中运用建模思想
高数中的概念较多,这无形中增加了学生对高数学习的难度。加上概念本身所具有的抽象性,让学生理解起来较为困难,其记忆的难度也同样予以增加。很多学生在学习高数的概念的时候往往会出现畏难情绪,容易让其本身的学习积极性受到打击。教师在进行概念教学时候融入建模思想,则可以让学生的学习更加形象化、具体化,有助于学生对概念的进一步了解和认识。
比如,笔者在讲授定积分概念的时候,便建立了两个模型。
(1)求变速直线运动的路程;
(2)变力沿直线做功。
对于问题(1)的求解,其可以利用公式:路程=速度×时间进行求解,但是此时问题的关键便在于速度的可变性。于是,教师在进行教学的时候便可以考虑“化整为零”,将时间段进行小区间划分,将其进行足够小时的分割,让每一个小区间段的速度接近一个常数,用这一小段的时间乘以速度。这样可以将每个小段内的路程相加得到路程的相似值。当然,如果想要得到更加精准的数值,则需要将时间进行更加精细的分割,其划分越细得到的数值越精确。通过计算我们可以得到路程的表达式为:
此表达式中v(t)是速度函数, fi是分割后的小段时间间隔,[ti-1,ti ]上任意选取一个时刻,△ti则是各个小段时间长, 是各个小段时间间隔中最大者。由此,可以得到问题(2)的表达式:
学生通过这两个表达式可以对定积分的定义有所认识,也能够通过自我总结了解到定积分的概念。
2.课外习题中对建模思想的应用
简单课堂中的教学难以让学生真正认识到建模思想的重要性,教师还需要将课堂践行延伸,让学生能够在进行习题练习的时候对建模思想进行灵活应用,一方面让学生能够对所学习的知识进行巩固,另一方面还能够让学生感受到高数学习的乐趣,同时还能够让学生感受到高数在解决实际问题方面的重要价值。
比如,教师在进行微积分教学的时候便可以运用“嫌疑犯确定”的习题让学生的学习兴趣得到提升。
某晚7:30分,发现一名被害者尸体,法医于晚上8:20赶到案发现场,测得被害者体温为32.6℃;1小时候后,该尸体被抬走,此时尸体温度为31.4℃,室内温度在此过程中始终保持在21.1℃。经排查,嫌疑最大者为李某,但是李某辩称自己无罪,并提供了证人说“下午李某一直和其在一起,5:00时候接到一个电话才离开”。而李某到被害人处仅需要5分钟时间,通过以上条件,请判断李某是不是杀人犯?
此题目能够最大化的激发学生好奇心,能够让学生将所学习的知识与问题结合在一起。通过牛顿冷却定律,我们可以知道,系统与环境的温差不大的情况下,系统温度变化率与系统温度和环境温度之差成正比,其数学表达式为:
其中T为系统温度,T0为环境温度,t为客观时间,k为散热系数。我们将尸体看成一系统,环境为死者的家,那么尸体的温度变化就会服从牛顿冷却定律。晚上8:20则成为t=0时刻,通过实测数据可以得出:
T(0)=32.6℃,T(1)=31.4℃
如果死者死亡时候的体温正常,那么T(t0)=37℃,确定死者的死亡时间t0,即求T(t)=37℃的解。如果李某在t0时间范围内没有与证人在一起,那么李某的嫌疑则不能够被排除。
高数的计算题转变成为一道有趣的悬疑题,可以让学生们的学习兴趣高涨,可以让学生温习所学习的知识,可以让学生们认识到建模思想的作用。
结语:
建模思想的应用让学生们的学习思维予以拓展,让学生们的学习兴趣得到提升,有助于学生们对高数的灵活应用。教师要对建模思想进行深入研究和探索,为培养新世纪的人才做好铺垫。
参考文献:
[1]江志超,程广涛,张静. 高等数学教学中数学建模思想的渗透[J]. 北华航天工业学院学报,2012,02:47-50.
[2]郭欣. 融入数学建模思想的高等数学教学研究[J]. 科技创新导报,2012,30:165-166.
