大规模MIMO系统中联合范数去噪与矩阵重构的DOA估计

朱翠涛，张正鹏

(中南民族大学 电子信息工程学院，武汉 430074)

大规模MIMO技术是第五代移动通信技术(5G)的核心部分之一，通过在基站部署大规模天线阵列即可生成增益高、宽度窄、可调节的赋型波束，可以大大减少对周边的干扰以及提高对目标用户定向传输的性能[1].在频分双工(FDD)模式下，进行波束赋型的前提条件就是精确估计用户的方位，而无线通信环境中存在着大量的多径干扰、复杂的衰落还伴随着用户设备的功率限制、较高的时延要求，这给DOA估计带来了难度，所以近年来的研究热点集中在低复杂度的DOA估计算法[2-4]以及少快拍甚至单快拍下的阵列信号处理方法[5,6].

移动通信环境下的DOA估计特点是接收数据有限、信号衰落严重、时延要求高，因此经典子空间类算法如：MUSIC算法[7]、ESPRIT算法[8]由于计算复杂度过高不适用于通信系统，而低复杂度的PM[9]算法和EPM(旋转不变传播算子)算法需要大量的快拍数来保证样本协方差矩阵的精度，同时基于传播算子的子空间构造也降低了DOA估计性能；非参数估计类方法如文献[4]中基于离散傅立叶变换的DOA估计算法，在覆盖用户数多的场景下DOA估计精度不够理想；文献[10]中提出了基于湮灭滤波器技术的低复杂度算法，该算法可以在仅数个快拍下工作，但信噪比要求较高；还有基于某些智能算法的DOA估计算法如文献[11]，通过分步估计的形式，有效降低算法的复杂度.

针对上述问题，本文提出一种联合范数去噪与Toeplitz矩阵重构的DOA估计算法，该算法首先根据阵列协方差矩阵的Hermitian特性借助矩阵范数估计其最大特征值进而估计噪声功率，然后对阵列协方差矩阵对角元素进行去噪，最后进行Toeplitz重排，使重构矩阵更加逼近理想阵列协方差矩阵.重构后的矩阵可以运用在子空间类算法中，在保留了原始算法高分辨率特性的同时，提高了在低信噪比、少快拍数条件下的估计性能.

图1 均匀线阵示意图Fig.1 Picture ofuniform linear array

1 系统和信号模型

考虑一个mmWave频段的大规模MIMO基站，采用FDD模式.如上图1所示，基站处配置M根天线并采用均匀线阵.同时基站下覆盖K个单天线用户，各用户发送信号互不相关，每个用户发送信号经由L条多径传播后到达基站天线阵列，阵元实际接收信号为各衰落信号叠加后的信号，每条多径的衰落系数为γ.信号入射角度为θk(k=1,2,3,…,K).

某时刻，基站天线阵列第i个阵元接收信号采样表示如下：

(1)

其中，γl,k表示第k个用户的第l路多径信号相比原始信号的衰落系数；θk表示第k个用户的方向，α(θk)表示该用户的方向矢量,为α(θk)=「1,ejπsinθk,ejπ2sinθk,…，ejπ(M-1)sinθk⎤T，sk(t)为该用户发送数据；ni(t)为第i个阵元上的加性高斯白噪声.矩阵形式为：

R(t)=GS(t)+N(t),

(2)

上式中,R(t)为阵列接收信号，S(t)为发送信号，N(t)为噪声干扰，G为衰落信道下的阵列流型，且有：

R(t)=[r1(t),r2(t),…,rM(t)]T,

(3)

S(t)=[s1(t),s2(t),…,sM(t)]T,

(4)

N(t)=[n1(t),n2(t),…,nM(t)]T,

(5)

(6)

2 联合范数去噪与Toeplitz矩阵重构的DEN算法

理论阵列协方差矩阵如下式：

Y=E{R(t)R(t)H}=GRsGH+σ2IM,

(7)

其中Rs=E{S(t)S(t)H}表示信号协方差矩阵，σ2为噪声功率，IM为M维单位阵.

式(7)可以看出理论上噪声污染仅存在于阵列协方差矩阵对角元素中，且协方差矩阵Y是一个Hermitian对称矩阵，而由于均匀线阵阵列流型的Vandermonde特性，协方差矩阵Y还具有Toeplitz特征[12].在实际情况下，一般用下式计算样本协方差矩阵：

(8)

式(8)中，N表示快拍数.

根据子空间理论，协方差矩阵Y应有K个不等的大特征值对应信源功率，有M-K相等的小特征值对应噪声功率.为了提高传统DOA估计算法性能，可以对样本协方差矩阵进行优化，常用方法可通过对样本协方差矩阵特征分解得到M-K个小特征值后求平均来估计噪声功率以此对样本协方差矩阵进行去噪，此方法不仅需要对高维矩阵进行特征分解，往往还因为样本协方差存在负特征值导致去噪效果较差；另外还可以通过理论协方差矩阵的Toeplitz特征来对样本协方差进行重排以优化样本协方差矩阵的结构.

下面将联合基于矩阵范数的低复杂度去噪方法与Toeplitz重构来实现对样本协方差矩阵的优化.

2.1 算法描述

若矩阵A为Hermitian矩阵，则其最大特征值满足[13]：

λmax≤‖A+αI‖m-α，

(9)

为了减小计算量，我们取m=1即矩阵的1范数，同时取α=‖·‖，对阵列协方差矩阵Y的最大特征值进行估计，计得到协方差矩阵最大特征值后，定义其平方根值为噪声功率的估计值.因此有

(10)

其中，α=‖Y‖1, 得到噪声功率估计值后，根据式(7)对Y的主对角线元素进行优化，得到理论上无噪的阵列协方差矩阵Yx：

(11)

根据前文的结论，理论协方差矩阵是一个Toeplitz对称矩阵.下面对Yx进行重排，使其结构逼近理想协方差矩阵.由于Yx仍是一个Hermitian矩阵，将其下三角部分每条斜对角线上的元素求和取平均，得到一组M×1维的数据向量v：

v=[v1,v2,…,vM]T,

(12)

(13)

以V为基础列向量进行Toeplitz重排，得到M维方阵YT.

至此完成对阵列协方差矩阵Y的重构，下面将YT代替原始协方差矩阵，使用子空间类算法进行DOA估计.

2.2 DOA估计流程

综上，以ESPRIT算法为例简述本文DOA估计算法流程，此处仅引用ESPRIT算法的结论而不推导其原理.

步骤1 由式(8)计算原始阵列协方差矩阵

步骤2 由式(10)估计噪声功率并由式(11)得到理想无噪阵列协方差矩阵Yx

步骤3 由式(12)、(13)计算列向量v，并以其为基础向量进行Toeplitz拓展得到矩阵YT

步骤4 将矩阵YT进行特征分解，根据ESPRIT算法估计旋转算子Φ，对Φ继续特征分解求得其特征值，由DOA计算式(14)得到用户DOA估计值：

(14)

其中，ωk表示旋转算子Φ的特征值，angle()表示求复数相角.

3 复杂度分析

本节按2.2节中的重构步骤1-3，对重构算法的复杂度进行分析，计算时以复乘运算次数为标准.

步骤1：计算原始阵列协方差矩阵复杂度为O(N2M)

步骤2：估计噪声功率复杂度约为O(M)

步骤3：Toeplitz重排涉及复数求平均运算，复杂度约为O(M)

因此DEN算法总复杂度为O(N2M+2M)，重构额外增加量为O(2M).虽然DEN算法带来了部分计算量，但是考虑到传统子空间算法的快拍要求往往是数百甚至数千，而经过本文重构后子空间算法可以在仅数十个快拍下以较高精度工作，并且对信噪比的要求也有降低.整体来说，DEN算法理论复杂度有所增加但是低信噪比、少快拍数条件下，经过重构的DOA估计算法精度优于未重构时，且在达到相同精度的时，DEN算法实际需要的复乘运算更少.

4 仿真分析

为了验证本重构方法理论分析的正确性以及算法的性能，本实验仿真了传统MUSIC、ESPRIT、PM算法及部分改进算法：TLS-ESPRIT(整体最小二乘旋转不变子空间算法)、EPM、PM，并比较了这些算法在重构协方差矩阵前后DOA估计性能的变化情况.

(15)

图2为EPM算法与TLS-ESPRIT算法两种算法改进前后的估计RMSE性能图曲线对比.从图2中可以看出在前述仿真条件下， 低信噪比时TLS-ESPRIT算法性能强于EPM算法，在高信噪比条件下性能相近.这表明EPM算法虽然复杂度降低，但却是以牺牲精度为代价的.两种算法在结合了DEN重构算法后，曲线趋势不变，TLS-ESPRIT算法改进后依然强于EPM算法，信噪比为8dB时二者达到相同精度.

图2 RMSE-SNR性能比较Fig.2 Comparison of RMSE-SNR performance

对EPM算法来说，由于算法本身较差的鲁棒性，导致性能较弱.TLS-ESPRIT算法性能在-10 dB至5 dB区间内快速上升，在5 dB左右几乎达到该算法的下界.两种算法改进前后对比表明DEN重构算法可以提高原始算法在较低信噪比情况下的性能.

图3仿真了算法改进前后，在信噪比固定为5 dB的情况下，算法性能随着快拍数增加的变化情况.从图3中可以看出，改进后的算法在100个快拍左右就几乎可以达到该算法的下界.在快拍数小于100的情况下，改进算法的RMSE要比原始算法RMSE低一到两个数量级.这表明DEN算法可以增强原始子空间算法在少快拍条件下的性能，且在大快拍条件下改进算法性能依然强于原始算法.

图3 RMSE-N性能比较Fig.3 Comparison of RMSE-N performance

图4仿真了EPM、TLS-ESPRIT两种算法改进前后的估计成功概率.从图4中可看出，当估计成功概率为1时，所需SNR由大到小排序为EPM>TLS-ESPRIT>DEN-EPM>DEN-ESPRIT，可以看出TLS-ESPRIT与EPM两种算法改进后的分辨门限有一定降低，大约降低了10 dB.

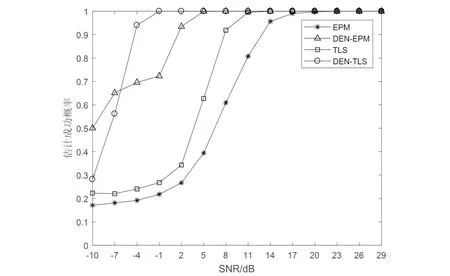
图4 估计成功概率比较Fig.4 Comparison of success probability

图5两图对比了DEN-EPM算法与EPM算法在500次蒙特卡洛实验下的估计结果分布散点图.仿真时SNR=0 db，用户数K=21，快拍数N=50.横坐标值为用户实际方位，纵坐标值为用户方位估计值.从图5.a可以看出，重构后的算法500次估计结果分布相对较为集中，说明性能较为优良且鲁棒.

对于均匀线阵，理论上用户DOA越偏离阵列法线方向，其估计结果的误差越大，反之越靠近法线方向，DOA估计算法性能就越优良，图5.a的仿真结果验证了这一客观事实.而图5.b反应了EPM算法在此仿真条件下的性能，可以看出此时EPM算法几乎无法正常工作，图中无法反映出用户DOA的数值.

图6仿真了MUSIC、PM和DEN-MUSIC、DEN-PM的归一化空间谱峰图情况，仿真时设置信噪比SNR=0 db，快拍数N=10.

从图6中可以看出在阵列协方差矩阵未重构前， MUSIC、PM算法的谱峰不尖锐、幅度不一、真实谱峰和伪封难以分辨，因此无法获知用户真实DOA方向，说明在信噪比较低、快拍数较少的情况下两种算法均无法实现DOA的有效估计；在应用DEN算法重构阵列协方差矩阵后，空间搜索谱峰正对用户DOA方向，伪峰几乎完全被消除，真实谱峰尖锐且易分辨.说明了DEN重构算法对提高阵列协方差矩阵在少快拍数情况下的性能具有明显正影响.

a) DEN-EPM b) EPM图5 估计结果分布散点Fig.5 Comparison of distribution scatter of estimation results

图6 归一化空间谱峰比较图Fig.6 Comparison of normalized spatial peak

5 结语

综上所述，针对移动通信环境中低信噪比、少快拍条件下DOA估计精度差问题，提出一种联合范数去噪与矩阵重构的算法.算法首先计算阵列协方差矩阵并通过其范数估计其最大特征值，用最大特征值的平方根值作为噪声功率估计值，来对阵列协方差矩阵进行去噪，再对去噪后的矩阵进行Toeplitz重排，实现对阵列协方差矩阵结构的二次修正.

仿真实验证明，本重构算法有效利用了阵列协方差矩阵中所包含的信息，在低信噪比、少快拍数的情况下提高了阵列协方差矩阵的精确度，与传统的子空间类算法结合后，可以相应提高传统算法的性能如：降低分辨信噪比门限、抑制伪峰等.复杂度分析表明虽然重构算法虽然引入了额外计算量，但增加的复杂度在可接受范围内.