体验表征 让数学理解更深刻——《认识千米》教学实践与思考

丁丹虹 张祖润（特级教师）

【课前慎思】

《认识千米》这一部分内容的学习，是真正培养学生量感的开始。虽然学生已有对长度单位毫米、厘米、分米和米的认识，但这节课对于学生来说更抽象。因为学生之前学习的长度单位都是身边很容易找到并且能够比划出来的，对于千米这样一个大的长度单位很难形成感性的认识。

怎样才能把这样一个抽象的长度单位让学生在充分的体验活动中进一步落实呢？体验活动除了走1 千米这样的直观感受，还可以怎样借助已经认识的长度单位进行推想？怎样才能让学生不仅能够有直观体验，还能通过以小估大的方法，对千米有更深刻的认识呢？基于以上认识和思考，笔者展开了《认识千米》的教学实践。

【教学过程】

一、复习引入，激发需求

1.回顾旧知。

师：同学们，我们的数学书的长大约是26 厘米，桌子的高度大约是7 分米。我们已经认识了哪些长度单位？

生：毫米、厘米、分米、米。

师：1 米大约有多长，能用手比划吗？

2.提出“千米”。

师：上个月，老师乘飞机去桂林，你知道飞机一般飞行时离地面有多高吗？

师：怎么都想到填千米啊？

师：原来千米比米大，是长度单位里面的一位新朋友，今天这节课我们就一起来认识千米。（揭示课题）

【设计意图：回顾以前学习过的长度单位，找到学生认知起点，然后引出新知“千米”。】

二、认识千米，体验度量

1.初识“千米”。

师：你对千米已经有了哪些了解？和同桌轻声说一说。

生：千米还可以叫公里。

生：1000 个 米 就 是1 个 千米。

2.再找“千米”。

师：生活中，你在哪里见过千米？

师：这些生活中的千米，表示什么意思？

【设计意图：基于学生认知起点介绍千米的知识，理解生活中千米的含义，让学生对1 千米到底有多长产生更大的体验兴趣。】

3.体验“千米”。

（1）根据10 米体验100 米。

师：老师今天还带来了一根彩带，估一估彩带有多长？

师：量一下，长10 米。

师：想一想，多少根这样的彩带连起来是100 米呢？你是怎样想的？

生：10 个,因为10×10=100。

师：是的，也就是10 个10 米是100 米。

师：根据10 米，你想象到100 米有多长了吗？其实在昨天，我们已经体验过100 米了，出示校园内100 米长的直道。

（2）根据100 米体验1 千米。

师：用看10 米想100 米的办法，我们还可以继续推想1 千米到底有多长？

师：想一想，多少个这样的100 米连起来是1000 米呢？为什么？

生：10 个，因为10×100=1000。

师：体验又要开始了，准备好了吗？100 米，200 米……1 千米。

师：1 千米有多长？说说你们的感受吧。

师：是啊！1 千米很长。

（3）自主体验1 千米。

师：老师还给大家准备了1千米的“作业单”。

作业单要求：算一算：在括号里填写合适的数。想一想：1 千米有多长？说一说：和同桌交流你的想法。

作业单：

①小明的一庹大约是1 米，（ ）个小朋友手拉手长度大约是1 千米。

②教室外的长廊长大约50米，（ ）个这样的长廊长度大约是1 千米。

从表2看出，对照周麦18小区平均产量113.12公斤，居第4位，比对照周麦18增产的品种有农大2011、郑麦1860、泉麦29，产量分别是119.55公斤、115.21公斤、115.09公斤，分别比周麦18增产5.68%、1.85%、1.75%，轮选166、珍麦3号、泰禾麦2号在本地区产量表现均不如周麦18。

③小红家到学校的距离大约500 米，（ ）个这样的距离大约是1 千米。

（4）回顾体验1 千米。

师：我们在生活中很多地方体验了1 千米，现在我们去操场上寻找1 千米。

师：昨天我们在操场玩了“小小快递员”的游戏，我们走的路程就是1 千米。在大家走完1 千米的时候，丁老师收集了三位同学的情况，我们来看。

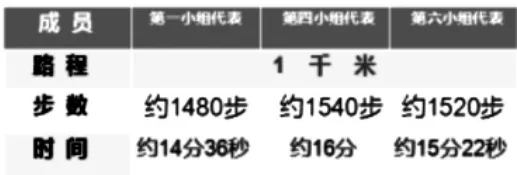
师：观察这组数据，比一比，你了解到哪些信息？

生1：第一小组走的步数最少，第四小组走的步数最多，有1540 步呢。

生2：他们都差不多走了1500 步左右。

师：那他们大约走了多少时间呢？

生：他们差不多都是15 分钟。

师：我们校区跑道走8 圈是1 千米，想一想1 圈是多少米？你是怎么想的？

【设计意图：学生对于千米的认识重在体验，只有通过丰富的体验，才能让学生对千米的理解更加深刻。这种体验通过有趣的游戏让学生在轻松愉快的氛围中更好地感受。对于大单位的体验并不一定能通过实践来完成，重要的是以小估大的方法教学，培养他们的估算能力以及想象推理能力，发展学生的“量感”。】

4．回顾梳理。

师：回顾刚才我们的学习，你认识千米了吗？有什么想说的？

师：在我们已经认识的长度单位中，千米是最大的。生活中很多地方都会用到它。

三、生活体验，应用拓展

1．基础练习。

（1）能给这些信息填上合适的单位吗？

天安门城楼大约高35（ ）

南京长江大桥铁路桥大约长7（ ）

京沪高速公路大约长1262（ ）

（2）快速填一填。

4 千米＝（ ）米

3000 米＝（ ）千米

9 千米○2000 米

600 米○2 千米

2．身边的1 千米。

师：千米在生活中很常见，身边的1 千米在哪儿呢？让我们一起来找一找。

3．身边的几千米。

师：这是一张地图，从我们学校出发，到中天钢铁体育馆大约是1 千米，照这样估计，从学校到青枫公园大约有多少千米呢？

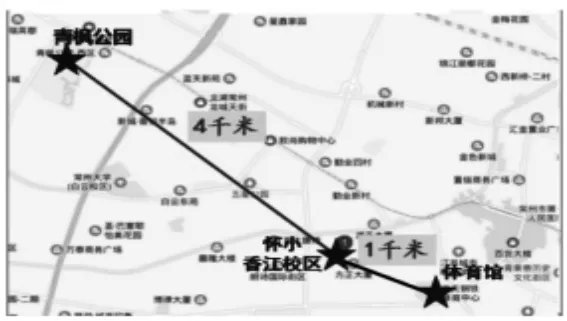
生1：3 千米。

生2：4 千米。

师：到底谁的估计最接近？让地图来告诉你。

师：如果把地图再缩小，我们可以看到常州的地铁整段路线，照这样估计，地铁路线大约是多少千米呢？

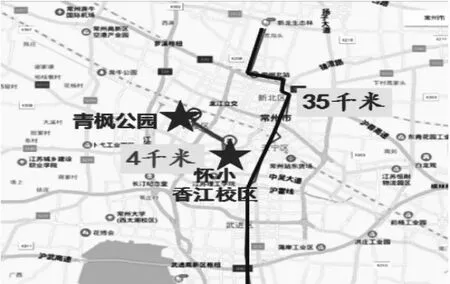
生1：28 千米。

生2：32 千米。

师：你们是怎么估的？

生：我是用手比划的，这个一份一份，差不多就是32 千米。

师：地铁路线总长度大约是35 千米，你估得准吗？

师：同样35 千米的路程，如果使用不同的交通工具行驶，它们各自需多少时间呢？

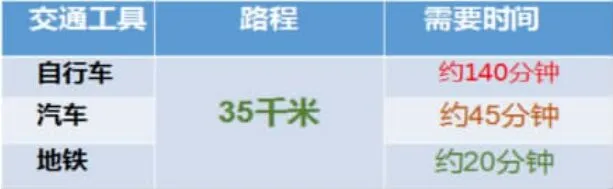
生：地铁很快。

师：人们创造了这么多丰富的出行方式，老师体验过2 个小时就行完1600 千米的路程，你们猜猜，我是乘坐什么交通工具才能做到的呀？

生：飞机。

师：我们现在的生活如此优越，这要归功于我们日益繁荣昌盛的祖国，归功于无数革命先烈，是他们流血牺牲奋斗出来的。

4.你知道吗？

师：说到革命先烈，不难联想到红军长征，他们翻山越岭，徒步行走两年时间，长达12500 公里。而我们走了1 千米就很累很累了，感觉口干舌燥想坐下休息了。他们是多么伟大啊！

师：你们认识孙悟空吗？他有一个很大的本事——翻筋斗云！他翻一个筋斗云就可以十万八千里，相当于54000 千米，飞机要足足飞行60 多个小时。孙悟空本事大不大？

师：但是，在科学世界里，有一位比孙悟空本事更大的“高手”——光。光1 秒就可以走过大约30 万千米的路程，相当于绕地球7 圈半，孙悟空就是1 秒内连翻5个筋斗云，也追赶不了光。

【设计意图：学生根据刚刚对于1 千米的感受估计身边的1 千米，很容易做出判断，但要想准确地估计几千米，就需要以1 千米做参照，用对比的方法进行估计后再验证，再一次让学生感受“量感”。尝试后让学生估计地铁路线总长度这个有挑战性的问题，学生能够利用正迁移进行对比估计，学生的推算能力得到了提升。再借助于交通问题的引入，引导学生将数学与学生的生活紧密联系起来。最后在学生感慨祖国日新月异的发展时，介绍红军长征、神话故事、科学世界中的光速，进一步丰富认知，完善理解。】

四、反思总结，完善认知

师：通过这节课的学习，你有了哪些新的收获呢？

【思考】

度量是数学的本质，是人们创造出来的数学语言，也是人们认识、理解和表达现实世界的工具。千米是一种基本的长度单位，用来刻画事物的具体长度，这种度量单位不是抽象的结果，而是借助一定工具制定的，是基于人对距离远近感知的本能。对于小学生而言，已知的长度单位是可以直接感知的，本节课我们试图借助各种体验活动，引导学生借助一定的参照来加深对千米的理解，获取更多有意义、有价值的体验。

1.直观体验，让数学理解更可视。

数学理解需要基于直观的感知，让学生在研究过程中获取可视、可感的体验，不断促进数学知识与生活理解的完美融合。本课中，在课前就让学生走“校园里的100 米”、“操场上的1 千米”，让学生对于这两个长度的步数以及时间建立一个直观的感受。再通过现场测量红绸带的长度，建立对10 米的直观感知，从而让学生对100 米、1000 米的概念建立形成基本的体验基础。有了这样的操作、体验、感悟，学生才会形成可视的直观感知，对1 千米长度的理解才会更深刻。同时，也有助于把抽象的长度与已有的直观经验进行对比、融合，让数学知识的学习与认知过程互相关联，建立更为清晰、更为直观、更为可视的数学理解。

2.场景体验，让数学理解更现实。

度量单位的生成是为了满足测量的需求，需要基于具体、现实、真实的场景，让学生产生共鸣、共通、共长的情景体验，才能使学生的数学理解与现实生活有效联接，形成真正有价值的数学学习行为。本课中，根据学生的学情，以学生身边熟悉的事物为切入点，贴近学生的生活圈，把最真实的情境还原，贴近学生思维经验，让学生在体验时做到有感受、有想象、有共鸣。经历了这样的体验过程，才能让学生主动把抽象的度量单位转化为自身认知结构中能理解的长度，加深对千米的理解，并在体验过千米后有意识、有层次地将“千米的认识”应用到实际生活中，在看、比、用、想的过程中加深学生对数学概念的理解。

3.推理体验，让数学理解更深刻。

庞加莱认为，如果没有测量空间的工具，我们便不能构造空间。度量单位就是把不同个体的度量方法标准化，有利于传播和交流，并表达度量的本质。那如何建立共同的标准、获取有意义的度量方法，从而形成有价值的数学理解呢？本课中，教师注重引导学生经历了确立参照标准、推理构建模型、想象形成认知的研究过程，在体验千米以及寻找千米时，都用到了大量的想象推理，给学生一个依据，让学生的思维获得一定的直观支撑，并借助感知估计“大约几千米”，这样的合情推理才会获得“量感”的体验，才能理解几千米到底有多长。在“你知道吗”的拓展渗透中，引导学生借助推理用千米作为参照认识更为宽域的认知世界，实现数感的飞跃与完善，从而提升学生的数学素养。