把握概念本质 深化数学认知——以“三角形底与高”的教学为例

管小冬

在区教师发展中心组织开展的青年教师优课评比活动上，一位青年教师执教了苏教版四年级（下册）《认识三角形》。其间，“认识三角形的底和高”这一环节的设计，引发了我对“认识图形”教学中，如何“准确把握概念本质，遵循认知逻辑展开教学”这一问题的思考。

【课堂】

在揭示“三条线段首尾相接围成的图形叫做三角形”这一描述性定义后。

师：生活中，你在哪些地方见到过三角形？

（学生交流后，课件出示房屋“人字梁”的图片）

师：屋顶的人字梁是三角形，你能量出它的高度吗？你量的是哪条线段？它有什么特点？

学生在独立观察、思考、交流后，明确中间这条从顶点到它对边的垂直线段的长度就是“人字梁”的高度。

课件从“人字梁”抽象出三角形，结合图示，出示三角形高和底的定义。

师：你能画出这个三角形（下图）底边上的高吗？

在学生活动、交流的基础上，明确画指定“底”上的高，就是从这条底边所对的顶点向底边画一条垂直线段。

师：发现没有，画三角形指定底边上的高，跟上学期我们掌握的“过直线外一点画它的垂直线段”本质上是一样的。

随后，教师又通过画高、量高等练习，进一步深化学生对三角形高的认识，巩固三角形高的画法。过程中，当指定底边不在水平方向时，部分学生画高出现了错误，教师又引导全体学生进行交流、辨析，强调三角形的底与高是相对应的。

【反思】

特级教师俞正强所著《种子课》一书中谈到，“如果将某一知识系统作为一棵树，这棵树的生长过程表现为若干节课，那么，一定有一些课需要莳也若子，充分理透脉络；……莳也若子的课，通常处于起点或节点，谓之种子课。”

认识图形是深入研究该类图形的重要起点，可谓之“种子课”。小学阶段“认识图形”一类课中，“认识三角形”又有着特殊而重要的价值与意义。一方面，“认识三角形”，不仅是学生进一步研究三角形内角和、分类及面积计算方法等内容的重要基础，更对学生认识、研究其他平面图形有着极为重要的作用。另一方面，教材对三角形的描述——“三条线段首尾相接围成的图形叫做三角形”，是极简洁明了的。但“越简单越复杂”，三角形是学生首次认识的边与角等元素间联系极为紧密的平面图形。对这种联系的深入探究，不仅可为学生积累更为丰富的数学活动经验，更有利于进一步发展数学思考，培养空间观念。

那么，如何展开这部分内容的教学，使之真正成为学生后续学习的“种子”呢？笔者以为，引领学生深刻认识“三角形的底与高”的含义及价值，是达成这一目标的重要途径。

一、充分感受高与底源于定量刻画平面图形的需求

我们对图形的认识，正经历了从定性把握到定量刻画这样的过程。即先在观察、对比的基础上，尝试用数学语言描述图形，将之区分于其他非同类图形；进而尝试通过数据来细致描述、刻画，将之区分于其他同类图形。“认识三角形”时，我们也正是遵循这样的认知逻辑，先“认识三角形的基本特征，初步形成三角形的概念”，再“认识三角形的高与底的含义”。

上述案例中，教师从“如何测量人字梁的高”这一问题出发，引导学生通过思考、操作与交流，认识三角形的高与底。这样的设计，看似立足生活经验，自然展开对“三角形高与底”的认识，然而，仔细推敲，在引导学生深刻感悟“高”与“底”是对三角形的定量刻画上，作用却未尽明显。

我们姑且不论现在的学生对“人字梁”有多少了解，仍借助其展开对“三角形高与底”的认识。不妨可以这样设计：课件呈现多个不同形状、大小的人字梁，引导学生在观察、对比中发现，因为底边长度不同、高度不同，所以人字梁的形状、大小也不尽相同。接着将人字梁抽象为三角形，请学生尝试画出刚才所说的“高”。再通过交流、辨析，明确“从三角形的一个顶点到对边的垂直线段是三角形的高，这条对边是三角形的底”。最后，请学生在测量出高与底的长度后，说一说它们分别是“底多少，高多少”的三角形。

值得注意的是，在“认识图形”的教学中，不少教师仅立足学生的几何直观，未能通过有效设计充分激发学生定量刻画图形的需求。如“认识长方形和正方形”时，直接告诉学生“通常把长方形长边的长叫做长，短边的长叫做宽。”

我们应该认识到，在“认识图形”的教学中，教师精心设计数学活动，让学生充分感悟数在具体刻画形方面的作用，有助于学生数学思考的发展和空间观念的初步形成。

二、深入认识高与底对定量刻画平面图形的意义与价值

面积与形状是我们在研究平面图形时重点关注的两个维度。就小学阶段学生认识的长方形、三角形、平行四边形、梯形这几个平面图形而言，数据的定量刻画对它们积与形两个维度的描述效果并不完全相同。

我们知道，一个二维的平面图形，需要使用两个数据（水平方向、垂直方向）进行定量刻画。区别在于，如果知道长方形的长和宽，我们不仅可以确定其大小，也能确定其形状。这与长方形的特征——“四个角都是直角”有关。即长方形中，边的长度是可变的，但角大小却固定不变。但如果知道三角形、平行四边形、梯形底和高的长度，我们仅能确定图形的大小（面积），却不一定能确定其形状。因为相较于长方形而言，这三种图形的边与角的联系更为紧密。而三种图形中，三角形尤甚之。角的大小改变会导致边的长度发生变化，形状也随之变化。反之亦然（相似形除外）。这也是三角形稳定性的数学内涵。基于这一点，我们不难理解，平面图形的定量刻画，本质上指向“积”的维度。

由此，在认识三角形的高与底后，我们可以设计以下数学活动，促进学生对三角形高与底意义与价值的理解，进而深化对三角形的认识。

1.数学游戏“三角形变变变”。利用课件动态呈现三角形的多种变化，引导学生观察变化前后的图形，说说什么变了，什么没变。在对比观察、交流辨析中感悟三角形边与角之间的密切联系，以及三角形形状改变，其相应的底、高也可能会发生改变。

2.数学游戏“三角形大猜想”。课件呈现三角形的一条底和一条高，请学生尝试想象这个三角形的形状（如下图）。

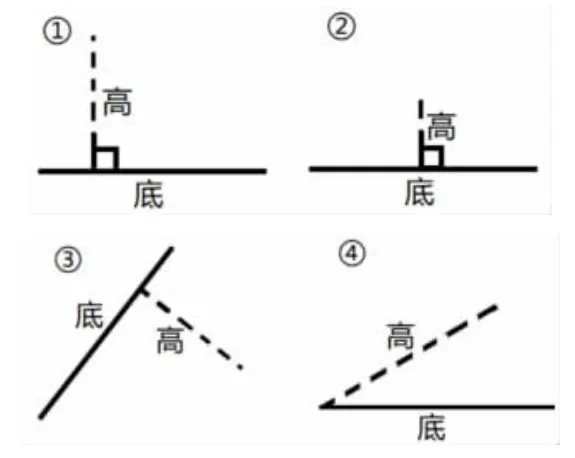
学生在观察、想象、思考中进一步体会底与高的对应性，及其对三角形的定量刻画作用。

接着，追问学生，如果一个三角形的底4 厘米，高3 厘米，你能想象出它的样子吗？试着在方格纸上画一画。进而组织学生交流发现，虽然三角形底与高的长度确定了，但其形状仍有多种可能。

随后，继续追问学生，如果长方形长4 厘米、宽3 厘米，它会有多种不同形状吗？课后思考：为什么长方形只有一种，而三角形却有无数种？这些底与高相同，但形状却不相同的三角形，在本质上又有什么联系呢？

“认识图形”教学中，我们应立足学生现有的生活经验与知识基础，遵循认知发展逻辑，引导学生在数学活动中，定性把握图形的基本特征，抽象、概括图形的概念；创设有效的数学情境，引发学生定量刻画图形的需求，在观察、对比、交流、辨析等活动中理解概念本质，深化数学认知。