例析破解三棱锥外接球问题的六种方法

广东省佛山市南海区黄岐高级中学

广东省广州市广东华侨中学(510000) 杨 墁

在高中数学教学中,立体几何是培养学生直观想象、逻辑推理、数学运算等核心素养的主要素材,也是高考考察的重点内容,而三棱锥作为空间中最简单的多面体,一直备受命题者的青睐,尤其是以三棱锥为载体求外接球的表面积和体积等问题,这类题目抽象,解法灵活多变,对学生的空间想象能力、逻辑推理能力以及运算求解能力要求较高,常令许多学生陷入困境.本文结合实例,根据实际问题中三棱锥的特点,谈谈解决三棱锥外接球半径的几种方法,以期对一线教师的教学提供参考.

方法一 利用长方体求三棱锥外接球半径

根据球的几何性质,到几何体各个顶点距离相等的点即为其外接球球心,因此,长方体的两条体对角线交点即为其外接球球心,体对角线长即为其外接球直径,设长方体的长宽高分别为a,b,c,则其外接球半径若三棱锥的各个顶点与长方体的顶点重合,则他们的外接球相同,故可利用长方体求三棱锥外接球半径.此类三棱锥大体上可以分为三类:墙角三棱锥、鳖臑、对棱相等型.

(一)墙角三棱锥有共端点的三条侧棱两两垂直,这样的三棱锥看起来像一个墙角,它具有长方体一个“角”的几何特征,我们可将其放置于长方体中进行研究.

例1(2019年高考全国Ⅰ卷理科) 已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,ΔABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )

图1

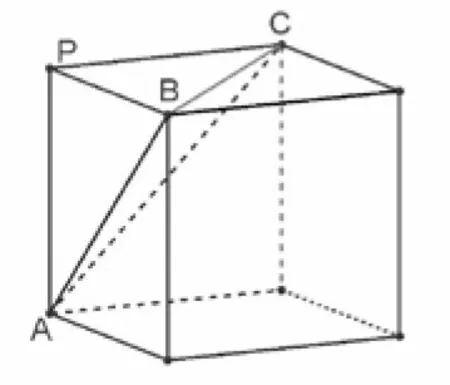
图2

解如图1所示,由题意知设PA=PB=PC=a,则由极化恒等式[1]得由向量的数量积定义及余弦 定理得由以上两式得因为∠CEF=90°,所以CE2+EF2=CF2,即解得故由勾股定理逆定理可得PA,PB,PC两两垂直,由此可以以PA,PB,PC为棱构造正方体(如图2所示),三棱锥P - ABC的外接球与正方体的外接球相同,故外接球的半径r=体积为选D.

(二)鳖臑有一个面是直角三角形,有一条棱与此面垂直,且垂足为此直角三角形的一个锐角顶点,《九章算术》中将这样的三棱锥称之为鳖臑.

例2(2008年高考浙江卷理科) 已知球O表面上的四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=则球O的体积等于____.

解因为AB⊥BC,DA⊥平面ABC,所以可将此三棱锥放置于长方体中(如图3所示),故此三棱锥的外接球与此长方体的外接球相同,则球O的半径体积

图3

(三)对棱相等型如果一个三棱锥的三对对棱长度分别相等,则可将其置于长方体中,使其四个顶点分别位于长方体的顶点上,六条棱分别位于长方体的六个面对角线上.

例3在三棱锥S-ABC中,则三棱锥的外接球的表面积为____

图4

解因为SA=BC,SB=AC,SC=AB,所以可将此三棱锥置于长方体中,使得S,A,B,C四点分别位于长方体的顶点上,如图4所示.

设此长方体的长宽高分别为a,b,c,则三式相加并化简得a2+b2+c2=14,故三棱锥的外接球半径为其外接球表面积S=4πr2=14π.

评注由上面几道例题可知,当一个几何体的几何特征满足另外一个几何体的局部特征时,可以将陌生复杂的几何体放到我们熟悉规则的几何体中去研究,利用规则几何体中的性质规律来解决复杂几何体的问题,从而化难为易.

方法二 利用直棱柱求三棱锥外接球的半径

如图5所示,在直三棱柱ABC -A1B1C1中,O1,O2分别为ΔABC,ΔA1B1C1的外心,点O为O1O2的中点,则利用全等三角形的性质易证O到直三棱柱各个顶点的距离都相等,故O点为直三棱柱的外接球球心,设ΔABC的外接圆半径为r,直三棱柱的高为h,则外接球半径

图5

对于侧棱垂直于底面的三棱锥,可将其放置于一个直三棱柱中,使得三棱锥的各个顶点与直三棱柱的顶点重合,因而他们的外接球相同,故可利用直三棱柱的外接球半径公式求出三棱锥的外接球半径.

例4(2018年佛山一模理科) 在三棱锥P -ABC中,侧面PAC⊥底面ABC,∠BAC=90°,AB=AC=4,PA=则三棱锥P-ABC的外接球的表面积为( )

A.24πB.28πC.32πD.36π

解由题意BA⊥面PAC,故可将该三棱锥放置于直三棱柱ACP -BC1P1(如图6),利用它们的外接球相同求出三棱锥的外接球半径.由余弦定理得则设ΔAPC的外接圆半径为r,直三棱柱的高为h,由正弦定理得所以该三棱锥的外接球半径其表面积为S=4πR2=36π,选D.

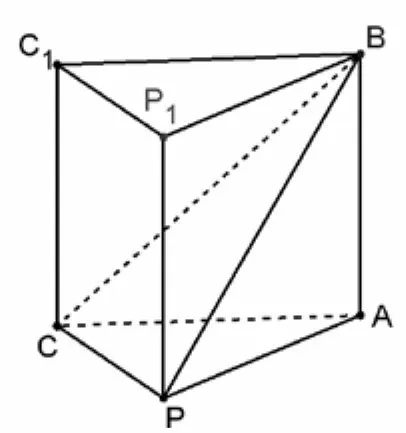
图6

图7

对应练习(2017年广州模拟理) 如图7,网格上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥外接球的表面积为( )(选D)

方法三 利用空间直角坐标系中两点间的距离公式

当三棱锥的外接球球心不好找时,可以考虑建立适当的空间直角坐标系,先写出三棱锥的各个顶点坐标并设出球心坐标和半径,再根据球心到各个顶点的距离等于半径这一性质,利用空间直角坐标系中两点间的距离公式建立方程组,从而解出球心坐标和半径.

例5(2018年佛山一模文科) 平面四边形ABCD中,沿直线AC将ΔACD翻折,当三棱锥D-ABC的体积取得最大时,该三棱锥的外接球表面积为____

解易知当此三棱锥的体积取得最大时,必有面ABC⊥面ACD,作BO⊥AC垂足 为O,连接OD,则可证DO⊥面ABC,结合余弦定理可得AO=BO=DO=1,CO=3,以O为原点建立如图8所示的坐标系,则A(0,-1,0),B(1,0,0),C(0,3,0),D(0,0,1).

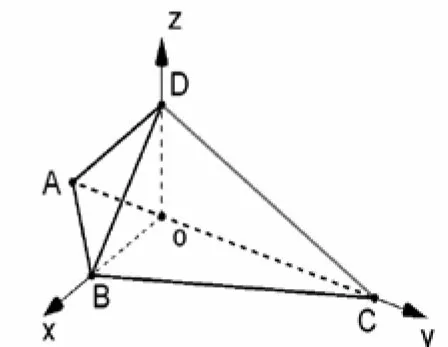
图8

设该三棱锥的外接球球心坐标为(x,y,z),半径为r,则根据球心到各个顶点的距离等于半径,由空间直角坐标系中两点间的距离公式得x2+(y+1)2+z2=r2,(x-1)2+y2+z2=r2,x2+(y-3)2+z2=r2,x2+y2+(z-1)2=r2,联立并解方程组得故该三棱锥的外接球表面积为S=4πr2=24π.

对应练习三棱锥P-ABC中,平面PAC⊥平面ABC,ΔPAC和ΔABC均为边长为2的正三角形,则三棱锥P-ABC外接球的半径为____.(答案是)

评注利用空间直角坐标系的方法,将复杂的空间问题代数化,弱化了对空间想象能力的要求,避开了抽象的几何推理,有效降低了求解难度,对空间想象能力较弱的学生来说不失为一种好方法.建系时要注意选择适当的点作为坐标原点,使得三棱锥尽可能多的顶点落在坐标轴上,这样可以减小后面解方程组的运算量.

方法四 利用两个面的“中垂线”的交点定球心

类比平面中线段中垂线的定义,在空间中,过ΔABC的外心作平面ABC的垂线l,则l上任意一点到ΔABC的三个顶点的距离都相等,在此我们称直线l为ΔABC的“中垂线”.

过三棱锥的底面作“中垂线”,则此“中垂线”上任意一点到底面三个顶点的距离都相等,再作其中一条侧棱的中垂面,则此中垂面与前面那条“中垂线”有且只有一个交点,该点到三棱锥四个顶点的距离都相等,即为球心.因此任意一个三棱锥都有且只有一个外接球.

类比三角形外心的作图方法,在三棱锥中,分别作其某两个面的“中垂线”,根据上述分析可知,这两条“中垂线”必交于一点O,且点O为外接球球心.球心一旦确定,问题往往便可迎刃而解.

例6已知在边长为的菱形ABCD中,∠A=60°,现沿对角线BD折起,使得二面角A-BD-C为120°,此时点A,B,C,D在同一个球面上,则该球的表面积为( )

A.20πB.24πC.28πD.32π

解由题意知ΔABD,ΔBCD为等边三角形,如图9所示,取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD,故∠AEC=120°,易知ΔABD,ΔBCD的外心O1,O2在AE,CE上,且过O1,O2分别作面ABD,面BCD的垂线,则垂线交点O即为所求外接球的球心,由对称性可知∠OEO1=∠OEO2=60°,在RtΔOEO1中,OO1=O1Etan 600=所以该球的表面积S=4πR2=28π.故答案为选项C.

图9

对应练习在四边形ABCD中,ΔABD和ΔBCD都是等腰直角三角形,沿BD把ΔABD翻折起来,形成二面角A-BD -C,且其大小为此时A,B,C,D在同一球面上,则此球的体积为____．(答案是)

评注实际问题中,一般选择侧面是特殊三角形(如:直角三角形或等边三角形)的面作“中垂线”,因为它们的外心比较容易确定,再根据两条“中垂线”的交点确定球心位置,这样可将空间问题化归到平面上解决,从而突破难点.

方法五 利用双半径单交线长公式

如图10,在三棱锥S-ABC中,面SAC垂直于面ABC,其交线长|AC|=l,ΔABC和ΔSAC的外接圆半径分别为r1,r2,则三棱锥S -ABC的外接球半径为

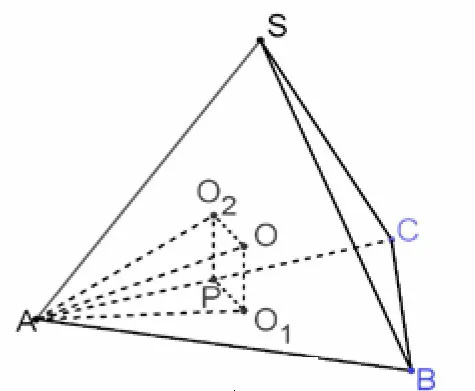
图10

证明分别过ΔABC、ΔSAC的外心O1,O2作所在面的垂线,由前面的分析可知,两垂线必交于一点O,且O为三棱锥S - ABC的外接球球心,取AC的中点P,连接PO1,PO2,AO1,AO2,AO,易证四边形PO1OO2为矩形,所以

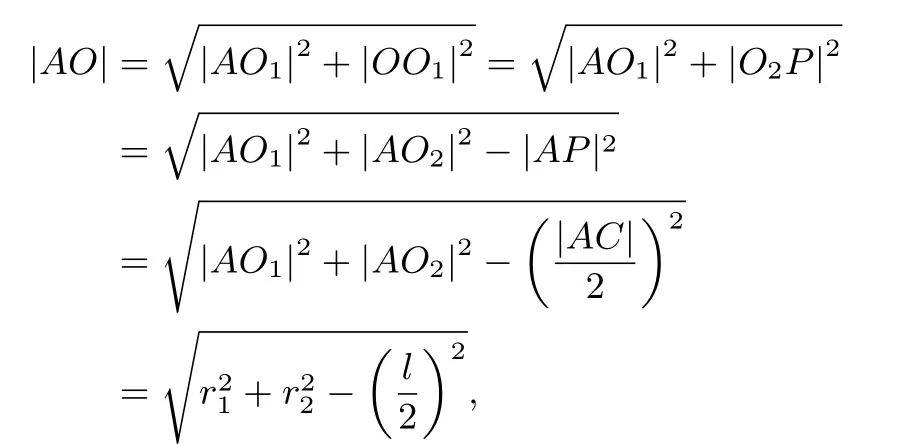
例7三棱锥S - ABC的各顶点都在同一球面上,AB=3,AC=5,BC=6,侧面SAB为正三角形,且与底ABC垂直,则此球的表面积为____.

解由余弦定理则sin ∠ACB=设ΔABC,ΔSAB的外接圆半径分别为r1,r2,由正弦定理得同理因为面SAB⊥面ABC,所以三棱锥S-ABC的外接球半径表面积

对应练习已知三棱锥A - BCD中,AD=BD=CD=2,∠BDA=∠CDA=120°,面ABD⊥面ACD,则三棱锥A-BCD的外接球的表面积为____.(答案是28π)

评注对于有两个面相互垂直的三棱锥,若这两个面所在三角形的外接圆半径可求且它们的交线长已知,则可利用这一公式迅速求出外接球半径.

方法六 利用等侧棱长公式

图11

图12

在过同一顶点的三条侧棱都相等的三棱锥P -ABC中,PA=PB=PC,作PD⊥面ABC,垂足为D,由三角形全等可证D为ΔABC的外心,则三棱锥P -ABC的外接球球心必在线段PD或PD的延长线上(如图11,图12),设外接球半径PO=AO=R,PD=h,ΔABC的外接圆半径分别为r,则DO=|h - R|,在RtΔADO中AD2+DO2=AO2,即r2+|h - R|2=R2,解 得此公式适用于侧棱长相等的棱锥,在此称为“等侧棱长公式”.

例8在三棱锥P -ABC中,若BA=BC=BP=则三棱锥P-ABC的外接球的表面积为____.

解如图13所示,在ΔABC中,由勾股定理可得故PA2+AC2=PC2,得∠PAC=90°,取PC的中 点D,则D为ΔPAC的外心,连接AD,BD,因为BA=BC=BP,所以BD⊥面APC,h-=BD=由于三棱锥P - ABC的三条侧棱长都相等,所以其外接球的半径表面积为

图13

对应练习(2019清华自主招生试题) 一个四面体的棱长分别为6,6,6,6,6,9,求外接球的半径.(答案是21)

评注上述公式可以推广到正n棱锥中:若正n棱锥的侧棱长为l侧,高为h,则它的外接球半径为