数论视角下的2019年全国Ⅰ卷参数方程选做题
2020-04-13广东省茂名市第一中学
广东省茂名市第一中学
一、试题呈现和考情分析
试题呈现(2019年高考全国Ⅰ卷文理第22题) 在直角坐标系xOy中,曲线C的参数方程为
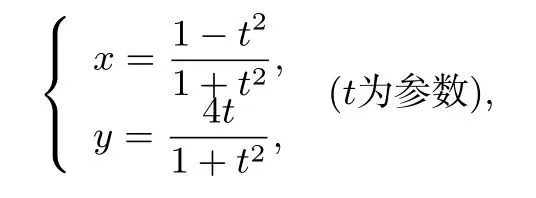
以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(1) 求C和l的直角坐标方程;
(2) 求C上的点到l距离的最小值.
考情分析2018年广东文科考生的参数方程选做题平均分是3.87,而2019年只有2.58 分;2018年广东理科考生的参数方程选做题平均分是5.23,而2019年只有3.53 分的.2019年的第22题的第一问,考生很不适应.虽然考生都知道要消参,可是里面的参数t太多了,他们无从下手.题目不能用常见的消参数方法,涉及到难度很大的消参技巧.考生第一问做不出,而第二问又是建立在第一问基础上的,尽管第二问难度不大,考生也是无题可做.所以第一问就导致了整道题目得分率不高.
二、数论知识背景和题目解答
不定方程x2+y2=z2叫做商高方程,也叫毕达哥拉斯方程.由于其形式漂亮,历史上有不少著名科学家(如毕达哥拉斯、柏拉图、欧几里德和我国清朝的罗士琳) 都对它进行过研究.《九章算术》第九章“勾股”也对勾股定理及其应用进行了讲解.

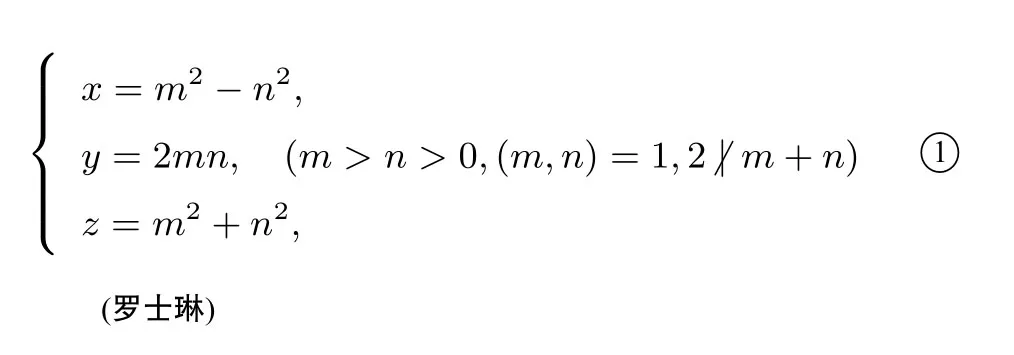
笔者最喜欢罗士琳的这个结果,很多初等数论教材也编入了这个结果,比如潘承洞和潘承彪编著的《初等数论》.当n=1时,它是柏拉图的结果即(m2-1)2+(2m)2=(m2+1)2.等式两边同时除以m2+1,得也即
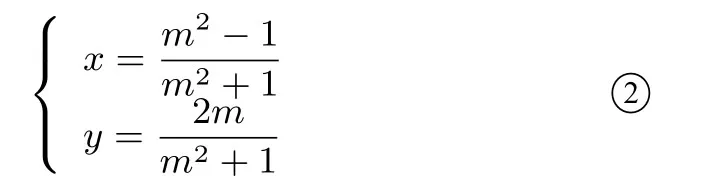

三、题目推广
推广1将中等式右边的4 推广到任意非零实数a,也即参数方程为将其配方成的形式所以化为普通方程就是1.化简得这也是[3]中的一道题目.
推广2推广1 只是中n=1 情形的简单推广,也可令n=2,n=3,···,甚至可以取n为任何实数.

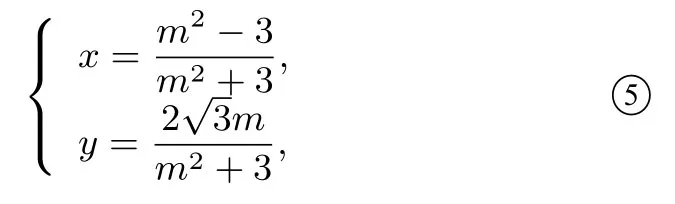
求其普通方程.
由上面分析过程可知答案为x2+y2=1(1).
如果我们想将3x,2y,推广到ax,by(00),那么我们可以将参数方程改为此时普通方程就是(ax)2+(by)2=1
当然我们也可以通过分子分母互换,调整系数等等来命题,感兴趣的读者可以变变花样来玩一玩.
推广3推广2是在的两边同时除以(m2+n2)2得到的,形式是X2+Y2=1,它是圆或者椭圆形式,那我们也可以在的两边同时除以(m2-n2)2或(2mn)2,分别可以得到和这两个式子结构是一样的,都可化为形如X2-Y2=1的双曲线形式.所以两个式子我们研究其中一种即可,不妨研究第一个式子,将其移项得也即参数方程为那么对应的普通方程为x2-y2=1.
类比推广2,我们也可以将题目难度逐步提升,先令n为任一确定的实数,比如时,得到下表.

表1 变式题解题步骤
四、一个副产品以及应用
由于商高方程x2+y2=z2的正整数解为其中m,n,都是正整数,且m >n.由于y=2mn一定为偶数,我们马上可以得到一个副产品.
定理边长均为整数的直角三角形,至少有一条直角边的边长为偶数.
下面我们用这个定理来快速解答一道北京大学自主招生题目.
题目(2019年北京大学自主招生) 已知x,y为整数,若(x2+x+1)2+(y2+y+1)2为完全平方数,则数对(x,y) 有( )组.
A.0 B.1 C.无穷多 D.以上全错
解令(x2+x+1)2+(y2+y+1)2=m2,则x2+x+1和y2+y+1是边长为整数的直角三角形的两条直角边.由定理可知,它们至少有一个为偶数.但是,由于x(x+1) 为两个相邻整数的积,其必为偶数,所以x2+x+1=x(x+1)+1必为奇数.同理y2+y+1 也是奇数,与它们至少有一个为偶数矛盾.所以无解,选A.
