不等式选讲模块中两个重要定理的应用
2020-04-13广东省汕头市第一中学
广东省汕头市第一中学
2019年高考全国Ⅰ卷和Ⅲ卷的不等式选讲问题均考察了不等式的证明,再度引起了我们对今年备考不等式证明这一内容的重视.说起不等式证明的常用方法,除了常规为我们所认知的作差法,分析法之外,自然会想起两个重要的工具——基本不等式和柯西不等式.本文从这两个定理的应用以及交汇的角度做了探讨,与大家共同研究学习.
一、基本不等式在证明中的应用
基本不等式是在人教A版教材必修5课本中《不等式》章节的一个内容,在选修4-5《不等式选讲》又列入其中,其公式本身在不等式证明中主要涉及二元与三元两种形态基本不等式.
从现行全国卷高考题考查分布来看,基本不等式主要考查的还是二元基本不等式,三元基本不等式的考查目前仅在2019年全国Ⅰ卷中有所涉及.
技巧一涉及三元不等关系,尤其次数非三次(或三次方根)的情况,常以二元基本不等式为主,利用三式相乘或者相加,达到证明目的.
例1设a,b,c均为正数,且a+b+c=1,证明:
证明(1) 因为a,b为正数,所以同理可得当且仅当时,等号成立,故
(2) 因为(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,由基本不等式有

点评本题的设计是常见的三元不等关系,但证明过程使用的却是普通的二元基本不等式,这里就需要学生在挑选和使用定理的过程中对两种形态基本不等式作一个比较,比如若使用三元基本不等式,则一般常涉及到三次式,或者三次方根,这两者本题都不涉及,这可以作为判断依据,少走弯路.另外,本题还有一个关键的关系,就是(a+b+c)2=a2+b2+c2+2ab+2bc+2ac这个展开式.利用这个展开式,结合基本不等式,我们不难推出以下二级结论,在日常训练中可以有意识让学生作为证明范本记忆使用.(考场上证明过程需要在解答中给出,这里是建议学习证明过程)
结论一ab+bc+ac ≤a2+b2+c2,(a,b,c ∈R),当且仅当a=b=c时等号成立.
结论二(a+b+c)2≤3(a2+b2+c2),(a,b,c ∈R),
当且仅当a=b=c时等号成立.
技巧二巧用定值代入,构造基本不等式.
在不等式证明或者最值问题中,条件往往都有“定值”条件的出现,而针对基本不等式的特点,常常可以利用“常数替换”配凑出基本不等式,从而简化证明与运算.
例2(1) 已知正实数a,b,满足a+b=4.求的最小值;
(2) 已知a,b,c为正数,且满足a+b+c=3,证明:9ab+bc+4ac ≥12abc.
解(1) 因为a+b=4,所以因为a >0,b >0,所以当且仅当即时等号成立.所以当时,取得最小值
(2) 要证9ab+bc+4ac ≥12abc,只需证即证即证即证因为所以当且仅当即时等号成立.原命题得证.
点评本题(1) 问使用的是基本不等式应用中的一个典型方法,学生一般不会陌生,然而作为一个典型的方法,其应用还不仅于此,到了(2) 问我们又将问题推广到了三元形态.由于(2) 问证明的是不等关系,故先从分析法对结论进行变形分析,再利用定值替换的方法进行配凑证明.定值替换的做法除了以“乘法”形式介入不等式,还可以结合式子特点,以“加法”形式介入,只要能构成基本不等式使用条件,同样能达到配凑效果.
例3(2013年高考全国Ⅱ卷) 设a,b,c均为正数,且a+b+c=1,证明:
(1)
证明(1) 证法同例1(2),略;
(2) 因为
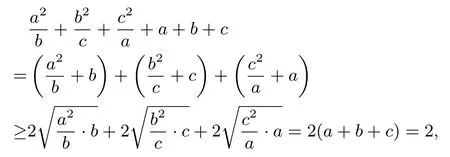
类似的做法,如果证明的不等关系是分式形态,且分子为常数的式子,也可以尝试定值替换达到常数分离或者消元的效果,化简不等关系.
例4已知a,b,c >0,且a+b+c=1.证明:
证明

技巧三涉及三元不等关系,且次数为三次(或带三次方根)的式子,可以考虑从三元基本不等式关系入手证明.
例5(2019年高考全国Ⅰ卷) 已知a,b,c为正数,且满足abc=1.证明:
(2)(a+b)3+(b+c)3+(c+a)3≥24.
证明(1) 要证注意到abc=1,即证ab+bc+ac ≤a2+b2+c2,只需要用上述二级结论的证明方法即可,略.
(2) 因为a,b,c为正数且abc=1,故有
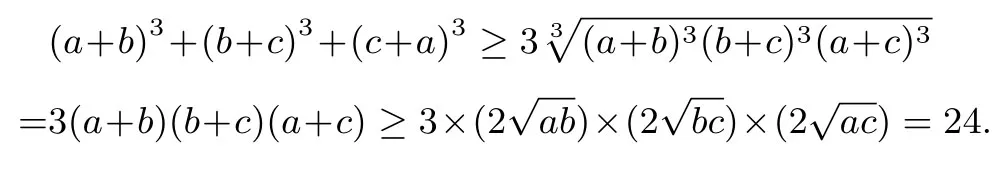
当且仅当a=b=c=1时等号成立
点评正如前面例1的点评中提到,使用三元基本不等式关系时,一般需要涉及“三元”与“三次”的条件,本题(2) 问恰好符合这一条件,所以考虑从三元基本不等式作为切入点,再分别使用三次二元基本不等式关系,最后需要验证的是多次使用基本不等式等号成立的条件能否同时满足.
二、柯西不等式在证明中的应用
柯西不等式是人教A版选修4-5《不等式选讲》中的教学内容,主要解决的是不等式最值以及相关证明问题.柯西不等式的证明与记忆,可以利用向量中的一个不等关系作为辅助,即|a·b|≤|a||b|,当且仅当a//b时等号成立.根据这个向量关系,对应二维向量和三维向量的坐标计算,可以得出二元形态和三元形态的柯西不等式,当然也可以推广到n元形态.这里着重介绍二元与三元形态的柯西不等式:
· 二元柯西不等式:
· 三元柯西不等式:
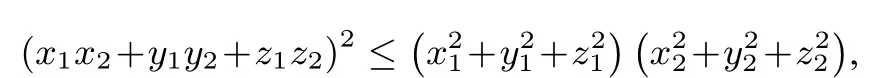
从柯西不等式的形态来看,其涵盖了不等关系中常见的“积”,“和”,“平方和”等关系,尤其是将“积求和”分离成“平方和”关系,是柯西不等式应用的最大亮点.利用这个特点,柯西不等式在不等关系的证明中,尤其是三元不等关系中可以发挥较大作用,下面先通过例6,例7展示柯西不等式的基本用法.
例6若x,y,z >0且满足x+y+z=1,求证
证明由柯西不等式得
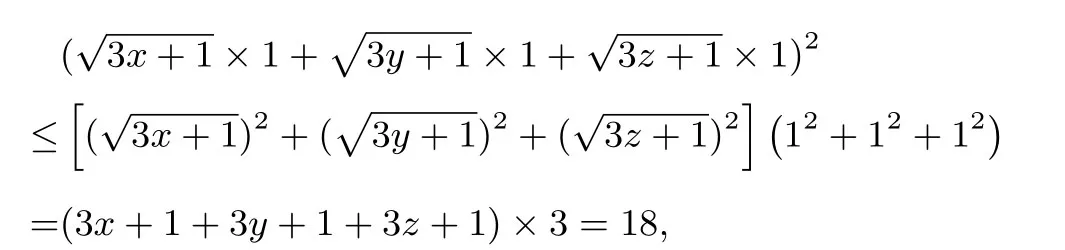
例7若x+2y+3z=6,求x2+y2+z2的最小值.
解由柯西不等式得(x+2y+3z)2≤(x2+y2+z2)(12+22+32),即36≤14(x2+y2+z2),所以x2+y2+z2的最小值为当且仅当即时等号成立.
点评通过上述两个例子,可以看出柯西不等式在使用过程中可以巧妙的根据变量系数的不同进行配凑,这点是基本不等式所难以做到的.学生如果能针对这个特点,由柯西不等式出发去构造完整的“柯西不等式体系”,那么证明的思路也能相应拓宽以及更为便捷.下面我们针对几道全国卷高考原题,通过对比不同的解法来阐述柯西不等式在这类问题中的应用.
例8(2019年高考全国Ⅲ卷) 设x,y,z ∈R,且
(1) 求(x-1)2+(y+1)2+(z+1)2的最小值;
(2) 若(x-2)2+(y-1)2+(z -a)2≥成立,证明:a ≤-3或a ≥-1.
解法一(1) 由于
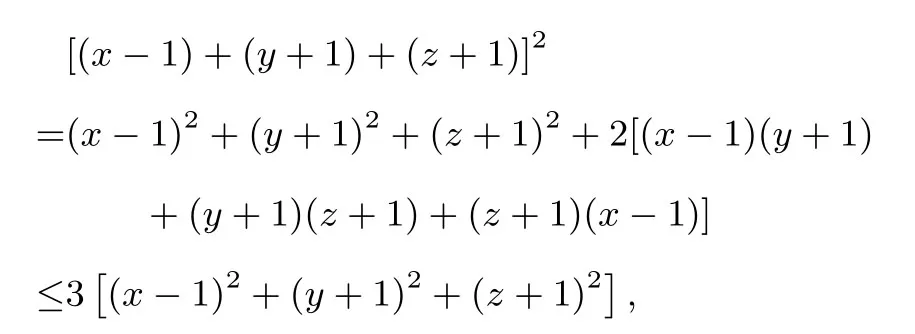
(2) 由于
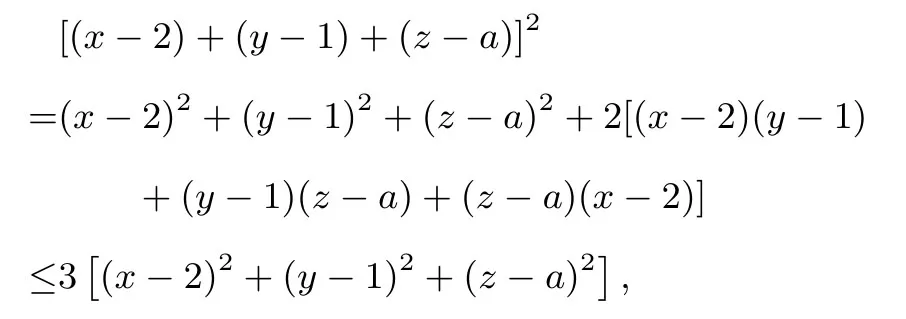
针对本题的解法,笔者在相关高考试题全解书籍或者网络搜索到的解法普遍采用的就是以上解法一,即先利用整体三元完全平方式展开得到不等关系后,再进行证明,实则文章前面所提到的二级结论二.下面的解法二是直接应用柯西不等式证明并解决该问题.
解法二(1) 由柯西不等式

(2) 由柯西不等式
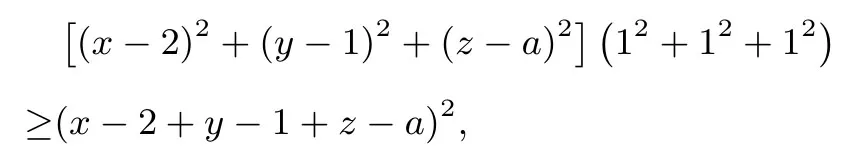
点评从解法二看来,如能找准柯西不等式的切入口,对本题的解决无疑提供了更加便捷的思路.而柯西不等式的应用关键在于巧妙的结合变量定值以及变量和系数之间的配凑,能利用好这点对问题的解决有很大帮助.我们在讲解这类问题的解法之后,还可以对不等关系再做变形,比如更改系数或者常数,那么就可以大大加强学生对这类问题的敏感度.又比如2017年全国Ⅱ卷的不等式选讲(1) 问,大家普遍的证明方法都是下文证法一,即将左边多项式展开后进行对a3+b3的配凑变形,再进行证明.下面我们也用柯西不等式的方法进行证明,给大家做个对比.
例9(2017年高考全国Ⅱ卷) 已知a >0,b >0,a3+b3=2,证明:
(1)(a+b)(a5+b5)≥4;(2)a+b ≤2(证明略).

证法一(1) 当且仅当a=b=1时,等号成立.
证法二(1) 由柯西不等式
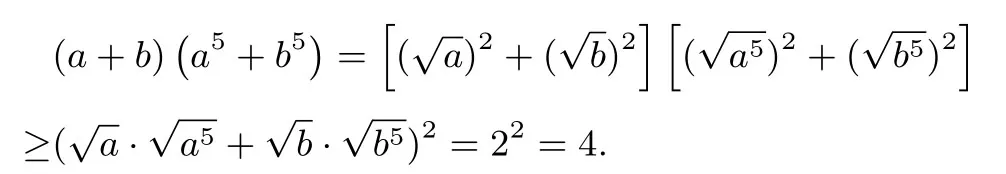
当且仅当a=b=1时,等号成立.
在之前叙述的使用基本不等式方法证明的例3第(2) 问,同样也可以使用柯西不等式的方法来进行证明.
例10例3的另一解法.
证明(1) 同例3,略.(2) 由柯西不等式

点评本题证法二巧妙地将不等式左边看成平方和关系,这正与柯西不等式中一边的平方和关系相吻合,只需要再构造另一组平方和,结合a+b+c=1,便可以配凑出“柯西不等式体系”,用其进行证明.
三、证明思路常见切入点
根据上述两个定理的应用与分析,当我们遇到不等式的证明问题时,可以先对不等式的条件,形态等特征做初步判断,从而快速找到证明的途径.笔者就证明问题的切入点,作以下归纳:
