2019年全国ⅠⅠ卷第22题探析*——兼谈极坐标与参数方程的教学

福建省龙海第一中学新校区

一、题目呈现

题目(2019年全国ⅠⅠ卷第22题) 在极坐标系中,O为极点,点M(ρ0,θ0)(θ0＞0) 在曲线C:ρ=4 sinθ上,直线l过点A(4,0)且与OM垂直,垂足为P.

(2) 当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.

二、试题分析

本题是选修4-4 坐标系与参数方程的内容.试题构思精巧,重点突出,切入点多.主要考查如何求直线,动点的极坐标方程,检测考生对极坐标是否有本质的了解,是否掌握直角坐标与极坐标的互化,是否掌握求动点的轨迹方程,是否具备思维的严谨性(轨迹方程中变量有一定的限制).试题涉及到两个动点,一个是主动点M,一个是从动点P,将动点问题巧妙地蕴含于极坐标背景当中,增加了试题的难度.考生要能够顺利解决问题必须具有良好的基础知识以及逻辑推理能力,数学运算能力.

三、试题解析

3.1 对第一步的解析如何求出直线l的极坐标方程?

方法1(先求出直角坐标方程,再转化为极坐标方程) 由于所以因为直线l与OM垂直,所以又直线l过点(4,0),所以直线l方程为整理得所以l的极坐标方程为或者

方法2(直接求出极坐标方程) 由已知有∠POA=设直线l上的一点Q(ρ,θ),(ρ ＞0,θ ∈[0,2π]).连接OQ,则三角形OPQ为直角三角形.有以下三种情况:

图1

图2

图3

比较上述两种解法,第一种方法是先求出直线l的直角坐标方程,再借助关系式x=ρcosθ,y=ρsinθ求出极坐标方程.这个思路是绝大多数学生容易想到的,也是绝大多数学生优先采用的方法.然而相比较于第二种方法直接设出点直线l上的一点Q(ρ,θ).第一种方法显得笨拙,繁琐.第二种方法显然直截了当,在运算上也大大化简.然而在实际解题中,缘何第二种方法被绝大多数学生忽略?这与教师对极坐标教学的方法不当有着直接的关系.在求解圆或者直线的极坐标方程时,教师鲜有设出动点的极坐标,然后根据等量关系得到极坐标方程,而是先求出圆或直线的直角坐标方程,然后借助关系式x=ρcosθ,y=ρsinθ求出极坐标方程.这样的教学方式不仅抹杀了学生的创造性思维,对于今后遇到求动点的极坐标方程试题更是不利.因为有些试题采用极坐标方法求解比采用直角坐标方法求解在计算上是可以大大简化的.因此,这就启发我们在教学时必须注重采用极坐标法求解动点极坐标方程的讲授,既要强调直角坐标方程与极坐标方程的互相转化,又要教会学生比较两者在计算上的优劣,而不是一味地强调所有试题都可以先转化成为直角坐标,再转化为极坐标.

3.2 对第二步的解析

第二步要求的是点P轨迹的极坐标方程.

方法1(先求出点P 轨迹的直角坐标方程,再求出极坐标方程) 如图4所示,由PO⊥PA可知点P在以OA为直径的圆上运动,该圆方程为(x-2)2+y2=4.又曲线C:ρ=4 sinθ,故该圆方程为x2+(y-2)2=4.两圆方程联立得交点坐标为O(0,0),E(2,2).由于P在线段OM上,且AP⊥OM,所以点P的轨迹方程为(x-2)2+y2=4,0≤x ≤2,0≤y ≤2.又x[=ρco]sθ,y=ρsinθ,故P的极坐标方程为

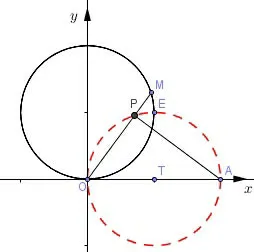
图4

方法2(直接求出极坐标方程) 设P(ρ,θ),在直角三角形OAP中,显然有关系式

对于第一种方法,点P在圆(x-2)2+y2=4 上运动是显然的,但轨迹是并不是整个圆.如图4所示,由于P在线段OM上,且AP⊥OM,所以点M只能在圆x2+(y-2)2=4.的右半部份运动.假设点M在圆x2+(y-2)2=4的左半部份运动,则没有符合题意的点P.换句话说,点P的轨迹只能是圆(x-2)2+y2=4 在圆x2+(y-2)2=4 内部的一段弧OE.因此联立两个圆的方程求出两圆交点O(0,0),E(2,2).从而确定点P的限制条件为0≤x ≤2,0≤y ≤2.至此,不难发现只有当动点M在圆x2+(y-2)2=4的右半部分且在点E(2,2) 上方运动时,才有符合题意的点P.

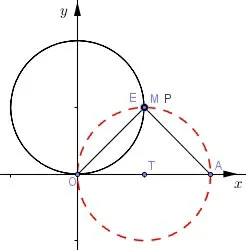
图5

图6

图7

在图5中,当动点M运动到点E处时,显然E,M,P三点重合.此时由于P(ρ,θ) 在直角三角形OAP中,显然有关系式ρ=4 cosθ.又点M在曲线C:ρ=4 sinθ上,所以有4 cosθ=4 sinθ,即此时θ最小.此当动点M往上运动时,显然θ在增大(图6),一直到当点M在y轴上时(图7),点P与点O重合,此时最大.故

下面借助Geogebra 软件验证.

图8

第二步:在圆上取点M,连接OM.

第三步:在输入框中输入A=(4,0),构造出点A,然后利用工具栏中的垂线按钮作出过点A且与直线OM垂直的直线AP.

第四步:右击点P,勾选跟踪;

第五步:右击点M,勾选启动动画;观察发现,动点P的轨迹是弧OE.如图8所示.

不难发现,本步属于典型的求动点的轨迹方程问题,只不过是将动点问题放置于极坐标的背景当中,增加了试题的难度.其难点在于如何确定点P的轨迹,如何求出变量的限制条件.解题的关键在于条件“P在线段OM上,且AP⊥OM”,结合动点M本身在圆x2+(y-2)2=4 上运动,确定动点M的运动轨迹只能是圆x2+(y-2)2=4的右半部分且在点E(2,2) 上方,确定动点P的轨迹只能是圆(x-2)2+y2=4 在圆x2+(y-2)2=4 内部的一段弧OE.只有把点M和点P的运动情况弄清楚了,才能确定极坐标方程中θ的限制条件,也才能真正的理解透本道试题,体会到命题者的良苦用心.这就启发我们在高三复习备考时,一定要重视如何求动点的轨迹方程,必须强调试题的动态性,要用动态的观点去解决问题,从而理解动点轨迹方程中变量的完备性与纯粹性.

四、试题变式

变式1(2018年高考全国ⅠⅠⅠ卷第22题) 在平面直角坐标系xOy中,圆O的参数方程为过点且倾斜角为α的直线l与圆OA,B两点.(1) 求α的取值范围;(2) 求AB中点P的轨迹的参数方程.

解析

(2)(方法1) 设直线l的标准参数方程为代入x2+y2=1 得

设A,B,P对应的参数分别为tA,tB,tP,则tA+tB=

设P(x,y),则所以

方法2如图9所示,设点P在以OT为直径的圆上运动.

图9

图10

如图10所示.所以AB中点P的轨迹的参数方程为

本题第二步也是典型的求动点的轨迹方程,但是要求的是动点轨迹的参数方程.方法1是借助直线的标准参数方程求解,方法2是先求出动点的直角坐标方程,再转化成参数方程.在方法2中,由PO⊥PT可知点P在圆上运动,但轨迹并不是整个圆.因为直线l与圆OA,B两点,所以点P的轨迹是圆在圆O内的一段弧MON,因此必须求出两圆的交点从而确定进一步得到参数方程

变式2(2017年高考全国ⅠⅠ卷第22题) 在平面直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.

(1)M为曲线C1上的动点,点P在线段OM上,且满足求点P的轨迹C的直角坐标方程;

(2) 设点A的极坐标为点B在曲线C2上,求ΔOAB面积的最大值.

解析(1)方法1:设M(4,y0),P(x,y).则即故由得x2-4x+y2=0(0).

方法2设P(ρ,θ),M(ρ0,θ),ρ ＞0.由16 得ρ·ρ0=16.又ρ0cosθ=4,所以ρ=4 cosθ.故点P的轨迹C2的直角坐标方程x2-4x+y2=0(0).

方法3设直线x=4 与x轴交于N(4,0),ΔONM为直角三角形.由可知NP⊥OM,即OP⊥PN,所以点P在以ON为直径的圆上,故点P的轨迹C2的直角坐标方程x2-4x+y2=0(0).

方法4由得设M(4,y0),P(x,y).则(x,y) ·(4,y0) =16,即4x+yy0=0.又故点P的轨迹C2的直角坐标方程x2-4x+y2=0(0).

本题第一步也是典型的求动点的轨迹的直角坐标方程方程.方法1是直接求出动点的直角坐标方程;方法2是设出点的极坐标,先求出动点的极坐标再转化成为直角坐标;方法3是充分利用平面几何性质(射影定理) 得到OP⊥PN,从而求出动点的直角坐标方程;方法4是借助向量的运算求解.不管是哪种方法,都是建立在对图形直观把握,整体感知的基础上,都要特别注意变量的限制条件.

五、教学启示

极坐标与参数方程是选修4-4的内容.解决极坐标与参数方程的问题主要有两种方法.第一是将极坐标方程化为直角坐标方程,参数方程通过消参转化为普通方程求解;第二是在充分考虑题设条件的基础上结合参数的几何意义,以及极坐标系下极角,极径的几何意义,利用极坐标系和参数方程知识直接解题.在实际教学中,要注重对基础的掌握,如直线、圆及椭圆的参数方程,参数方程与普通方程的互化,极坐标方程与普通方程的互化,使学生认识到三种方程不过是对同一种曲线的不同表述,认识三种方程本质的一致性.除此以外,更要注重引导学生用参数方程和极坐标方程来思考,解决问题,强化学生用极坐标与参数方程的知识解题的意识,开拓视野,提升数学思维能力.最后,要加强对动点轨迹方程试题的训练,尤其是采用多种思路求解同一道动点轨迹问题,在此过程中要注意变量的限制条件,培养学生的严谨性.