重本求质“圆”形毕露——以圆为背景巧解平面向量最值问题

浙江省永嘉县上塘中学

向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁[1],是高中数学知识网络中的一个交汇点,而高考命题往往在交汇处设计试题.笔者通过对浙江高考试题和近年的温州市高三模拟考试题的研究,发现一类向量与圆结合的问题,这类问题以向量表征圆,通过数形结合巧解平面向量最值问题.这类问题比较综合且灵活,很多同学处理起来不得要领,下面结合具体问题谈谈挖掘向量中的圆的常见方式和具体应用.

一、向量表征“圆”形毕露

1.圆的向量表征式

(3) 两者联系实际上,由平面向量的极化恒等式结合向量加减法的几何意义可得

(其中O为AB的中点),A,B点固定时得这说明模长式和数量积式殊途同归.

2.追根溯源

模长式圆比较好理解,即符合圆的定义——平面上到定点的距离等于定长的所有点组成的图形叫做圆;下面从圆的方程的角度给出数量积式圆的证明:

以AB点的连线方向为x轴,线段AB的中点为坐标原点建立直角坐标系,设A(-m,0),B(m,0),P(x,y),则整理得x2+y2=m2+l,故当时,点P的轨迹即以AB的中点为圆心,以为半径的圆.

3.提升推广

二、考题链接,重本求质

例1(2018高考浙江卷第9题) 已知a,b是平面向量,e是单位向量．若非零向量a与e的夹角为向量b满足b2-4e·b+3=0,则|a-b|的最小值是( )

思路分析关键在于对b2-4e·b+3=0的处理,为保持结构的统一性,可将3 看成3e2,对于b2-4e·b+3e2=0可配方或因式分解,结合圆的向量表征方式,解法便呼之欲出.

图1

图2

解法一因为b2-4e · b+3=0,所以配方得所以设由可得,b终点B在以C为圆心,1 为半径的圆上,又a与e的夹角为则a终点A在过点O且与OC所在直线所成角为的两条射线上,如图1所示,的最小值的几何意义即为圆C上任一点B到定射线OA上任一点距离的最小值,由几何性质可知该最小值为圆心C到OA的距离减去圆C半径,即

解法二b2-4e·b+3=0,即b2-4e·b+3e2=0,因式分解得(b -3e)·(b - e)=0,设所以由此可得b终点B在以EF为直径的圆上,又因为a与e的夹角为a终点A在过点O且与OC所在直线所成角为的两条射线上,如图2所示,余下与解法一相同,不重复叙述.

解法三因为b2-4e·b+3=0,所以b ·(b -4e) =-3,符合数量积式圆,设由可得即可知b终点B在以OF的中点M为圆心,为半径的圆上,又因为a与e的夹角为a终点A在过点O且与OM所在直线所成角为的两条射线上,如图3所示,余下与解法一相同,不重复叙述.

例2(2019年温州高三一模第9题) 已知向量a,b满足则a·b的取值范围是( )

图3

思路分析关键在于对a2+2a·b+2b2=8的处理,直接配方导致多出b2不好处理,考虑到还有已知条件可先消去b2前的2,再对其进行配方,得到模长式圆,或者直接将代入,再因式分解得到数量积式圆,再结合向量数量积a·b的几何意义进行求解.

解法一a2+2a·b+2b2=8 变形得配方得故设由可知b的终点B在以O为圆心,为半径的圆上,过点B作直线OA的垂线交于点F,如图4,由投影的意义得a · b=2MF,而投影所以选B.

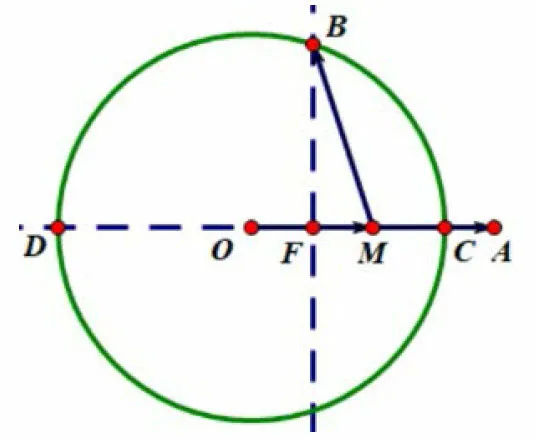
图4

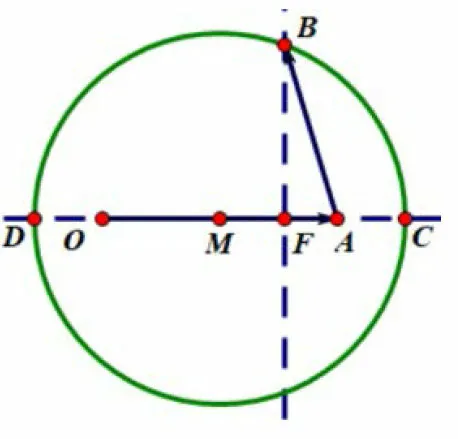
图5

解法二由a,b满足|a|=2,a2+2a·b+2b2=8,得a·b+b2=2,因式分解得(a+b)·b=2,符合数量积式圆,设由(a+b)·b=2 可得即可知点B在以OA的中点M为圆心,半径为的圆上.如图5,由投影的意义得a·b=2AF,余下与解法一相同,不重复叙述.

例3(2019届高三温州二模第7题) 在平面上,e1,e2是方向相反的单位向量,则的最大值为( )

思路分析该题中圆的向量表征比较显然,将模长式圆|a|=2和数量积式圆(b-e1)(b-e2)=0 结合到了一起,画出图形,利用|a-b|的几何意义便可求解.

解析设则 由可得a终点A是在以O为圆心,2 为半径的圆上,由(b-e1)(b-e2) =0,即可得b终点B是在以CD为直径的圆上,且CD=2,如图6,即为两个同心圆上的动点A,B间的距离,可知最大值为两圆半径之和,所以选D.

图6

当然,例1还有其他解法,比如坐标法等,可参考文献[3],例2、例3同样解法多样,但无论哪种方法,最终还是回归到了圆中,掌握圆的向量表征方式至关重要.且从以上的最近一年的浙江高考题和温州市高考模拟题的解答可以看出,理解了圆的向量表征方式后使得问题的解决变得明朗化,可谓众里寻他千百度,尽在圆中,重向量本求几何质,“圆”形毕露,数形结合思想在其中彰显得淋漓尽致.

三、题源回溯,研究高考

自浙江省数学高考独立命题以来,笔者认为以下例题与上述题目有异曲同工之妙:

例4(2011年高考浙江卷理科第15题) 若平面向量α,β满足且以向量α,β为邻边的平行四边形的面积为则α和β的夹角θ的取值范围是____.

例5(2008年高考浙江卷理科第9题) 已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c) ·(b-c) =0,则|c|的最大值是( )

例6(2008年高考浙江卷文科第16题) 已知a是平面内的单位向量,若向量b满足b·(a-b)=0,则的取值范围是____.

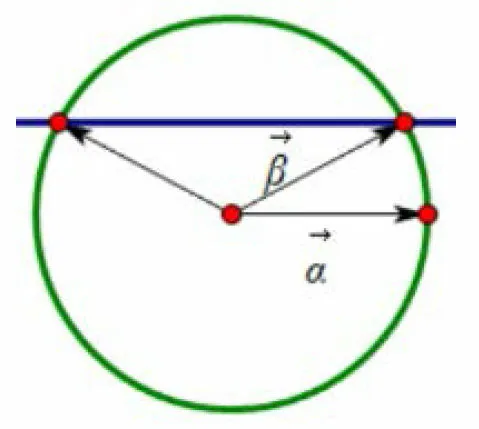
图7

例5中由(a-c) ·(b-c) =0 可联想到数量积式圆,即设由(a-c) ·(b-c) =0 得0,所以c终点C在以AB为直径的圆上,如图8,故|c|的最大值等于的最大值,问题转化为圆上任意一点C到圆上一定点O距离的最大值问题,又a,b是平面内两个互相垂直的单位向量,故直径结合图形可知选C.

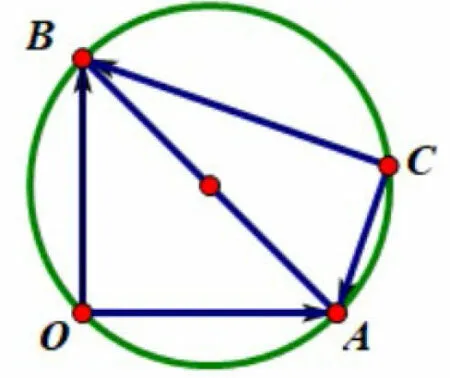
图8

例6中,由b ·(a - b)=0同样可联想到数量积式圆,设即所以b终点B在以OA为直径的圆上,问题又转化为圆上的任意一点C到圆上一定点O距离的最值问题,如图9,又故的取值范围是[0,1].

图9

当然,上述问题还有其他解法,但是可能费时费力,结合圆的向量表征方式数形结合解题体现了问题的本质,“圆”形毕露.浙江高考命题每年都推陈出新,表面看似复杂,但研究历年浙江高考真题就会发现一些内容会反复考察,这些题目往往会有自身独特的特点.若仔细研究探讨,由形而思,从中可以归整理纳出一定的解题技巧和方法,合理构造,然后秒杀.

四、螺旋上升,问题设计

本文中选取的高考题和模拟题难易程度不一,2008 高考浙江卷理科第9题、2008年高考浙江卷文科第16题和2019年届温州市二模第7题中的圆的表征就比较显然.一以向量模长固定时,即动点到定点的距离为定值,结合圆的定义便可发现圆;二以数量积是零时,两向量互相垂直,即动点与两定点构成直角,结合圆的性质便可发现圆.而2018年浙江高考第9题和2019届温州市一模第9题中的圆的表征就比较隐晦,需事先进行配方或因式分解等变形处理,再进一步研究点、圆、线相互间的位置关系.当然,学生不可能一步就掌握要领,要想训练学生数形结合思想和问题转化能力,基于向量隐形圆的阶梯式的问题设计就显得尤为重要.为了让藏在向量中的圆“圆”形毕露,给出由浅入深的问题设计如下:

问题1已知b,e是平面向量,e是单位向量,向量b满足(b-3e) ·(b-e) =0,则|b|的取值范围是____.

问题2已知平面向量a,b,c满足且(a-c) ·(b-c) =0,则的取值范围是____.

问题3已知a,b是平面向量,e是单位向量,若非零向量a与e的夹角为向量b满足b2-4e·b+3=0,则的最小值是____.

问题4等边ΔABC的边长为3,平面上的动点P满足则的取值范围是____.

设计思路结合2008年高考浙江卷理科第9题,对2018年高考浙江卷第9题进行重新设计,可将其简单化,即去掉向量a的背景,将向量b的条件b2-4e·b+3=0 更明朗化,即(b-3e) ·(b-e)=0,直接求|b|的取值范围,问题便可转化为圆上的任意一点C到圆外一定点O距离的最值问题,这是第一个阶梯.结合2019届温州市二模模拟题,对2008年高考浙江卷理科第9题进行重新设计,加之同心圆背景,可将问题转化为圆与圆的位置关系,这是第二个阶梯.有了这些铺垫以后,2018年高考浙江卷第9题便是要迈的第三个阶梯,要将条件适当变形处理,又考查直线与圆的位置关系.数量积式圆可以借助恒等式如此隐晦,让人不禁思考对于模长式圆是否也可隐晦处理,让学生自己去发现,这便是第四个阶梯,比如可借助平面向量基本定理及定比分点向量公式.

五、回顾反思,提升素养

著名数学家苏步青说:“学习数学要多做习题,边做边思索,先知其然,然后知其所以然.”[4]然而,严峻的现实是,许多学生虽然做了大量的习题,但遇到类似的题目仍不知所措,“这道题好像哪里见到过,但是还是不会做”是学生的普遍反映,“这题,我讲过好几次了,学生为啥还是不会写”是一线教师们的口头禅,为什么会有这样的偏差？笔者认为,高考数学题既考查学生的“四基”,又考查“四能”,还考查“数学学科核心素养”,如果学习中仅就题论题,对问题的理解只停留在知识的表面上,而没有深入分析理解其中所蕴含的本质,那么做再多的习题,也只是事倍功半.

解题是一种复杂的思维过程,解题是数学学习者的基本功,解题也是学数学的主要功课之一.针对浙江高考数学中的一类平面向量问题,代数法可以有效考查学生的运算能力,培育数学运算核心素养,但有时过于繁琐,而从几何的角度考虑问题更直观,“圆”形毕露,数形结合,提高解题效率,有利于培育直观想象、逻辑推理、数学抽象等核心素养,因此上面高考题和模拟题的解法笔者采用的均是几何法,揭示了该类问题背后的几何实质——圆.

另外,在平时的教学中,教师应该多多进行高考题目的研究,从中寻找关联点,寻找通性,关注题目背后所隐藏的知识内容,将各知识点有机融合,形成微专题复习,培养学生数形结合等重要数学思想,提升数学核心素养,借助向量的知识研究圆便是很好的素材,充分理解和把握圆的向量表征方式十分重要,不仅要理解掌握模长式圆和数量积式圆的形式,还要关注到两者间的联系.