他山之石，也可攻玉

葛雨春

[摘  要] 类比是运用已有的学习经验去解决新的类似问题的一种学习方法. 其作为数学学科最重要的思想方法之一，让学生掌握类比的方法，是帮助学生构建认知图式、提高问题解决能力的重要途径. 文章以初中几何为例，探讨了几种类比方法的实践应用.

[关键词] 初中数学;类比思想;初中几何;课堂教学

类比是一种学习的方法. 在数学领域，类比作为数学思想之一，占据着重要的地位，影响着学生学习数学的全过程. 类比思想的具体表现，可通过学生学习的不同阶段反映出来. 其中，在小学阶段，类比的主要特征是模仿;在初中阶段，类比的主要特征是运用学习经验，解决同类问题;在高中阶段，类比的主要特征是知识迁移;而在大学阶段，类比则表现在能力迁移层面. 由此可见，让初中生掌握类比的思想方法，对他们当下以及未来的学习和成长具有重要的意义. 类比的方法有很多种，教师可以引导学生在解决不同问题时运用不同的类比方法，以此拓宽学生的视野，培养学生的灵动思维. 本文以初中几何为例，探讨了几种类比方法的应用.

围绕“线少”与“线多”进行类比

几何的研究重点是空间结构，而构成空间结构的要素之一，是“线”. 对于初中生来说，初次接触难度较大的几何知识时，他们往往会对错综复杂的几何线感到力不从心，进行计算时容易出错，主要原因在于，初中生缺少缜密的思维，分析问题时缺乏条理性，难以区分相似问题之间的差异，过于依赖概念或定义，从而加大了解题的难度. 为此，教师可从“线”出发，引导学生围绕几何线展开类比：首先明确“线”在问题中所表达的含义;其次，理顺解题思路.

例1  如图1，点D在△ABC的边AB的延长线上，AE和BE分别平分∠CAB和∠CBD. 设∠C=x°，∠E=y°，求证：y=■x.

分析？摇 很多学生在解决这一问题时，容易把注意力放在“∠C=x°，∠E=y°”这一已知条件上，分析“AE和BE分别平分∠CAB和∠CBD”与“∠C=x°，∠E=y°”之间的关联性，而忽略了“线”在这一问题中所占据的重要地位. 严格来说，“线”是构成“角”的重要前提. 分析本题中包含了几条线，及它们的主次，“线”越多，本题的难度越大，而探析主要“线”与“y=■x”之间的联系，才是解决这一问题的正确突破口，如AE和BE对∠CAB和∠CBD的影响. 在这样的前提下，我们可以引导學生回归到最初的解题思路上，从而分析已知条件.

解答？设∠CBE=∠DBE=a°，∠CAE=∠EAB=b°，则有2a=2b+x，a=b+y. 所以2（b+y）=2b+x，解得y=■x.

例2？摇 如图2，点D在△ABC的边AB的延长线上，AE和AF三等分∠CAB，BE和BF三等分∠CBD. 设∠C=x°，∠E=y°，试用x表示y.

分析 此题与例1相比，明显加大了难度. “AE和AF三等分∠CAB，BE和BF三等分∠CBD”，随着“线”的增多，角也增多了，学生分析问题的过程也将更加烦琐. 为此，教师可以引导学生运用已有的学习经验，借鉴解决例1的思路和方法，仍然从“线”入手，首先分析本题中包含了哪些“线”及其主次，如此题仍然以△ABC为研究对象，但增加了AF和BF两条线，虽然如此，仍然可以采用相同的方法来解决本题.

解答设∠CBF=∠FBE=∠EBD=a°，∠CAF=∠FAE=∠EAD=b°，则3a=3b+x，a=b+y. 所以3（b+y）=3b+x，解得y=■x.

初中生的几何知识基础较为薄弱，缺乏对数学思想方法的认识及应用能力，为此，教师可从类比思想的简单应用入手，首先让学生了解什么是类比思想方法，其次由浅至深，引导学生以“线”为切入点，从“线少”向“线多”类比，逐渐加大解题难度，让学生通过类比不断提高能力层次，从而提高学生的问题解决能力.

围绕“形内”与“形外”进行类比

“形”是几何的灵魂，学习初级几何知识或解决简单的几何问题时，无论是平面图形还是立体图形，都需要先从“形”入手，分析几何图形的特征，梳理已知条件，来确定解决问题的思路和方法. 而“形”也是数学的另一个思想方法——数形结合的构成要素之一，以形定数，以数解形，使抽象的数学问题具象化，对提高学生的解题效率具有重要意义. 因此，教师可围绕“形”引导学生进行类比，以培养学生的数学思维.

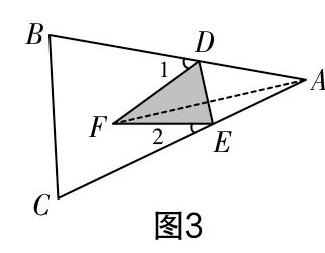
例3？摇 如图3，在△ABC中，D，E分别在AB和AC上，如果沿着DE折叠△ABC，点A恰好落在△ABC内的点F处，求证：∠1+∠2=2∠DAE.

分析此题最大的特点是涉及的角众多. 面对本题，学生易被折叠前与折叠后△ABC的变化及其角的相互联系所误导，从∠ADE和∠DFE的视角来分析本题，而忽略了所有计算活动都在△ABC的形内完成，即点A落在点F上之后，∠DFA，∠DAF与∠1，∠2之间的关联. 因此，教师可以引导学生以“形”为切入点，运用所学的翻折变换相关知识，来解决“形”的折叠问题.

解答？摇 连接AF，则∠1=∠DFA+∠DAF，∠2=∠EFA+∠EAF. 所以∠1+∠2=∠DFE+∠DAE. 又由翻折知∠DFE=∠DAE，所以∠1+∠2=2∠DAE.

例4 （在例3图形的基础上，由“形内”向“形外”拓展）如图4，在△ABC中，D，E分别在AB和AC上，沿着DE折叠△ABC，使点A落在△ABC外的点F处，探究∠1，∠2，∠BAC三者之间的关系.

分析 本题的突破口仍然在于点A与点F的重叠上，然而，即便有了例3的解题经验，但惯性思维会使初中生仍然将注意力停留在∠ADE和∠DFE层面，而忽略了点F在△ABC外，以及折叠后出现的∠DFA和∠DAF. 与“形内”解题不同，在“形外”解题时学生会遇到很多的隐性条件，尤其是因几何图形变化而衍生出新的图形. 如本题中，沿DE向外折叠，连接AF后便给出了解题的基本方向，即∠1=∠DFA+∠DAF，∠2=∠EFA+∠EAF.

解答连接AF，则∠1=∠DFA+∠DAF，∠2=∠EFA+∠EAF. 所以∠2-∠1=∠EFA+∠EAF-∠DFA-∠DAF=∠EFD+∠EAD. 由翻折知∠EFD=∠EAD，所以∠2-∠1=2∠EAD=2∠BAC.

對于初中生来说，“形内”解题难度较小，关键在于学生能否建立起“形”的概念，能否在面对一道几何题时首先由“形”入手，建立起契合几何知识特性的解题观，进而通过类比迁移，运用几何的思想方法，来解决学习和生活中遇到的几何问题. 因此，围绕“形内”与“形外”进行类比，是提高学生数学素养的重要途径.

围绕“一般”与“特殊”进行类比

在几何图形中，一般图形所涵盖的范围较大，如正方形、长方形、三角形等. 相较之下，特殊图形往往是由一般图形变化而来的，如上述案例中的图形折叠. 因此，教师可以引导学生围绕“一般图形”与“特殊图形”进行类比，充分运用已有的知识经验，简化遇到的几何问题，用类比的思想方法进行数形结合，从而降低解题难度，提高解题能力.

例5如图5，△ABC是等腰三角形，AB=AC，点P在BC上，PD⊥AB于点D，PE⊥AC于点E，CF⊥AB于点F，求证：PD+PE=CF.

分析面对这道几何题，教师可以引导学生从三角形的概念入手，首先将该题转化为一般图形，运用之前学过的几何基础知识，从垂直的角度，先连接AP，然后通过分析图形得出PD，PE，CF均为三角形的高这一结论，最后通过计算确定三者之间的数量关系.

解答？摇 连接AP，因为S■+S■=S■，又PD，PE，CF分别是△APB，△APC和△ABC的高，所以■·AB·PD+■·AC·PE=■·AB·CF. 又AB=AC，所以PD+PE=CF.

例6？摇 （在例5的基础上，教师可以将一般图形转化为特殊图形）如图6，△ABC是等腰三角形，AB=AC，点P在BC的延长线上，PD⊥AB于点D，PE⊥AC于点E，CF⊥AB于点F，探究PD，PE，CF之间的数量关系.

分析 严格来说，初中生对几何中一般图形的认识和理解根深蒂固，相关概念较为简单，因此能够充分地应用于解决新问题中. 如例5，△ABC作为“一般图形”，学生对相关概念较为熟悉，能够从PD，PE，CF入手，通过三角形的高来化解问题. 而转化图形（例6）后，学生通过已有经验，运用类比的方法来解决关于“特殊图形”的复杂问题，也会更加得心应手，且能提高解题的准确度和有效性.

解答 连接AP，因为S■+S■=S■，又CF，PE，PD分别是△ABC，△ACP和△ABP的高，所以■·AB·CF+■·AC·PE=■·AB·PD. 又AB=AC，所以CF+PE=PD.

一般来说，初中生的数学思维模式还较为简单，对于已经接触过的数学思想方法，很多时候还不懂得如何运用，为此，教师可以立足初中生的实际情况，由简入繁，让学生围绕“一般”和“特殊”进行类比，以此来巩固学生的已学知识，帮助学生建立新的认知图式.

结语

在教学实践中，可应用的类比方法还有很多，如几何图形的“同侧”与“异侧”类比，点、线、面的类比，图形构成元素的类比，等等. 总之，作为一线教师，应充分认识类比思想在初中生学习数学过程中的重要性，进而因地制宜，灵活运用数学类比思想方法，为学生打造一个类比迁移的学习平台，从而为学生当前和以后的学习奠基，推动学生在数学的道路上一路前行.