孟德尔遗传实验蕴含的科学思维
2020-03-27周忆堂
周忆堂
摘 要:孟德尔遗传实验研究蕴含了丰富的科学思维.对其进行深入剖析,引领学生感悟蕴含其中的批判性和创新思维、逻辑推理方法及建模思想,是培养学生学科核心素养的有效途径.
关键词:归纳概括;批判创新;演绎推理;建模
著名分子遗传学家雅各布(F. Jacob)曾经说过,“通过孟德尔,生物学现象突然需要了数学的严密性,一个完整的内部逻辑通过方法论、统计学的处理和符号的标记加给了遗传学”[1].孟德尔的遗传实验给遗传学的研究提供了严密的实验思路和科学的实验方法,可作为培养学生科学思维的良好素材.由于大多数中学教师没有从事过深入的科学研究,对科学研究的方法缺乏足够的理解和深刻的体验,教师在教学过程中常常是按照教材上“概念—原理—应用”的顺序将豌豆杂交实验连同两大遗传规律都作为现成的知识结论传授给学生,很少从科学观、方法论等多方面进行挖掘.在这种情况下,深入剖析孟德尔实验研究的过程,引领学生感悟蕴含其中的科学思维,是培养学生学科核心素养的有效途径.
1 归纳与概况
在遗传学史上,自从1760年可尔罗伊特(J.G.Koelreuter)第一次仔细地进行植物(烟草)杂交试验后,格特纳(C.F. von Gaertner)等许多学者都相继做了此类工作.但是很长时间以来,他们习惯于把生物遗传现象从整体(整株植株)出发笼统地进行考察,并研究杂种和亲本间、杂种相互间的全部特征和结构.由于研究对象过于复杂,加之受早期“融合遗传”等传统遗传学思想的影响,得出的结论也只能是一些笼统的概念,未能得出关于遗传学的规律性认识.孟德尔选择豌豆做杂交试验,选择了七对有明显区分的性状(即质量性状)进行观察统计.这样,他把简单的特征从整个个体中独立出来.孟德尔在单个性状的遗传试验中计算出,显性性状出现的频率是3/4,再把全部的试验结果综合起来,求出“具有显性性状和隐性性状的类型的数目之间,有一个3比1的比例”.这种将个别的、特殊的性状作单独考察,最终上升到一般規律性的认识,实际上就是一种归纳法.归纳法有它的局限性,但孟德尔做了大量的正反交试验,充分分析试验所得的材料和数据.此外,他还竭力主张对多种植物进行试验,尽量避免由于选材的特殊而得到片面的结论.
2 批判与创新
从上述规律性现象(3∶ 1分离比)到其深层的本质机理(遗传因子分离)的探索,需要认识主体发挥批判与创新思维,透过自然现象,洞察其本质,揭示其真谛.恩斯特·迈尔曾说过,“也许生物学中没有别的领域在其发展中否定错误观点和信条比在遗传学中更重要”[2].从开始的“活力论”,到“融合遗传”,再到“颗粒遗传”,遗传学理论在批判与创新中不断发展完善.孟德尔生活的时代正值“颗粒遗传学说”盛行,早期主张是:在每个细胞中对应于某一单位性状存在着无数完全相同的决定因子,每一决定因子的许多复制物可能同时传给生殖细胞,即:多重颗粒观点.如果情况如此,杂交就不会出现一贯不变的比值.这一假定使明确透明的遗传学说的建立和发展几乎成为不可能.孟德尔另辟蹊径,从批判性思维和创新思维的视角出发,结合豌豆杂交实验结果,对这种“多重颗粒观点”大胆提出质疑,做出“单个微粒”假说:生物性状由遗传因子决定,遗传因子呈颗粒状,在体细胞内成双存在,生殖细胞内成单存在;杂交后,颗粒仍保持独立;在杂种产生配子时,不同的遗传因子仍各自分离开来,并被分配到不同的配子里,完整地传递给下一代.这一思想,既有力否定了“融合遗传”的传统思想,又批判发展了“颗粒遗传”观点.孟德尔运用这种批判性、创新性的科学思维模式,对现象背后的机理做出大胆、合乎逻辑的假设,对他的前辈们只是模模糊糊感到的东西提出了明确的解释,为遗传学理论的发展和完善奠定了重要基石.
3 演绎与推理
孟德尔时代,细胞学说刚起步,还不可能通过显微观察、基因定位等技术手段来直接验证遗传因子分离的假说.所以,人们没法问:假说是否真实?而只能问:假说是否能为其它问题提供符合事实的解释?这就是演绎推理.如果假说能从逻辑上演绎出相关事实,那么该假说是成立的.常见的演绎推理有三段论、假言推理、联言推理等.假言推理是指有一个前提为假言判断,通过另一个前提对假言前提的“前件”或“后件”的断定推出结论的演绎推理,常用于科学假说的验证过程.孟德尔通过测交试验,对假说进行了验证,其推理过程如下:
[前提1] 如果F1能产生2种不同类型的配子,并且数量相等(前件),那么用F1和隐性亲本杂交,子代应该出现2种性状,且分离比是1∶ 1(后件).[假言判断]
[前提2] F1和隐性亲本杂交,子代出现2种性状且分离比是1∶ 1.[实验事实]
[结论] F1能产生2种不同类型的配子,并且数目相等.
4 模型与建模
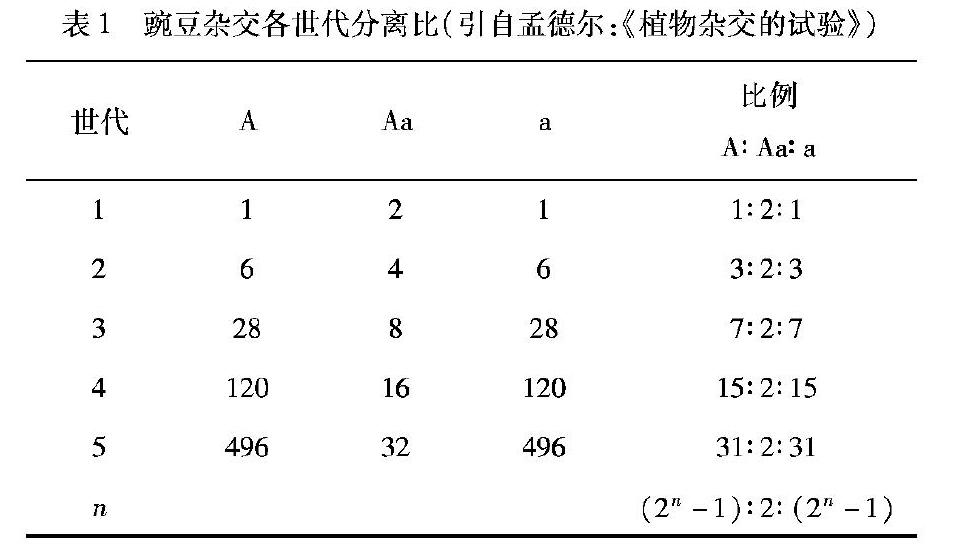
认知心理学家认为,表象更适合思维活动的进行.模型属于表象.孟德尔在研究过程中引入了符号模型,将试验的结果用符号和简单的公式表示.如用“A”代表显性性状,“a”代表隐性性状,“Aa”代表杂种类型,则“A+2Aa+a”即表示具有两个可区分性状的杂种所产生后代的展开系列.通过建模找到遗传因子和性状间的关系,依据模型进行推导、分析,做出预测.在此基础上,孟德尔进一步用了数学模型.在对单个性状分析时,孟德尔通过归纳,建立数学模型,并指出,“假定每一代中每一株植株只提供4个种子,则在n代中,A∶ 2Aa∶ a等于(2n-1)∶ 2∶ (2n-1)(见表1).在分析同时具有多对可区分性状的后代时,孟德尔设以n代表可区分性状的数目,则3n就代表组合系列的项数,4n为属于这系列的个数,而2n就代表保持稳定的组合数[3].正是在这一系列工作的基础上,孟德尔总结了关于杂种性状(3∶ 1)n的遗传规律.
综上所述,孟德尔遗传实验蕴含了丰富的科学思维.从结果的分析、问题的提出到假设的形成与验证,孟德尔充分发挥批判、创新思维,巧妙利用逻辑推理方法,合理运用建模思想,方才取得如此伟大的科学成就.教师在教学中,引领学生感悟孟德尔遗传研究中所蕴含的科学思维,有助于学生学科核心素养的培养与发展.
参考文献:
[1]李难. 孟德尔学说在科学方法论上的贡献[J].哲学研究,1985(03):51-57.
[2][美] 恩斯特·迈尔.生物学思想发展的历史[M].成都:四川教育出版社,2010.
[3][奥地利] 孟德尔等.遗传学经典文选[M].北京:北京大学出版社,2012.
(收稿日期:2019-11-16)
