多孔介质球向渗流的渗透率分形模型
2020-03-14王世芳
王世芳,吴 涛,夏 坤
(1.湖北第二师范学院物理与机电工程学院, 武汉 430205;2.光学信息与模式识别湖北省重点实验室, 武汉工程大学数理学院, 武汉 430205)
流体在多孔介质球向渗流问题广泛存在于诸如油气藏工程、地下水资源的合理利用、地热的开发与利用、生物体组织与器官等实际应用工程领域,越来越多地引起了广大科研工作者的关注.渗透率是表征流体在多孔介质中输运特性的重要参数之一,该参数对于油田、地下水资源等工程应用领域有重大的研究意义.目前有诸多文献利用分形理论的方法研究了流体在多孔介质中的流动特性,取得了一定的研究进展[1-6].员美娟[7]基于毛细管模型,研究了牛顿流体在分形多孔介质中的平面径向流和平面平行流,分别得出了平面径向流和平面平行流的流量、流速及渗透率的表达式.张斌等人[8]基于平行毛细管模型研究了幂律流体在多孔介质中平面平行流的流动特性,提出了幂律流体平面平行流的渗透率模型.徐鹏等人[9]利用蒙特卡罗数值模拟的方法研究了牛顿流体在多孔介质中流向井中心的径向流渗透率模型,并通过与渗透率解析模型比较从而验证数值模型的正确性.截止目前,虽然人们对流体在多孔介质输运特性的研究取得了较大进展,但是上述文献主要研究的是各种流体在多孔介质中的平面平行流和平面径向流时的流动特性,对于流体在多孔介质中球向渗流的研究却不多.苗同军等人[10]利用分形理论研究了考虑毛细压强效应影响后多孔介质球向渗流的相对渗透率,得到相对渗透率是饱和度、湿相与非湿相分形维数、多孔介质的微结构参数和毛细压强的函数.然而,苗同军的模型认为多孔介质是由一束平行的圆形毛细管组成,没有考虑毛细管的截面形状.在自然界中大部分多孔介质孔隙形状多样化,存在着圆形毛细管、矩形毛细管、三角形毛细管甚至非规则形状的毛细管.本文主要工作是基于分形理论,提出牛顿流体在由任意形状毛细管组成的多孔介质中球向渗流的渗透率分形模型.
1 多孔介质球向渗流的渗透率的分形模型的提出
三维多孔介质的球向渗流广泛存在于油气藏储集层,当油气藏储集层只打开很小一部分层段时,流动区域存在沿球面径向流动情况,即流体从外向井筒中心流动,如图1所示.其中r为储层中的某点到井中心的径向距离,r0为井筒半径.
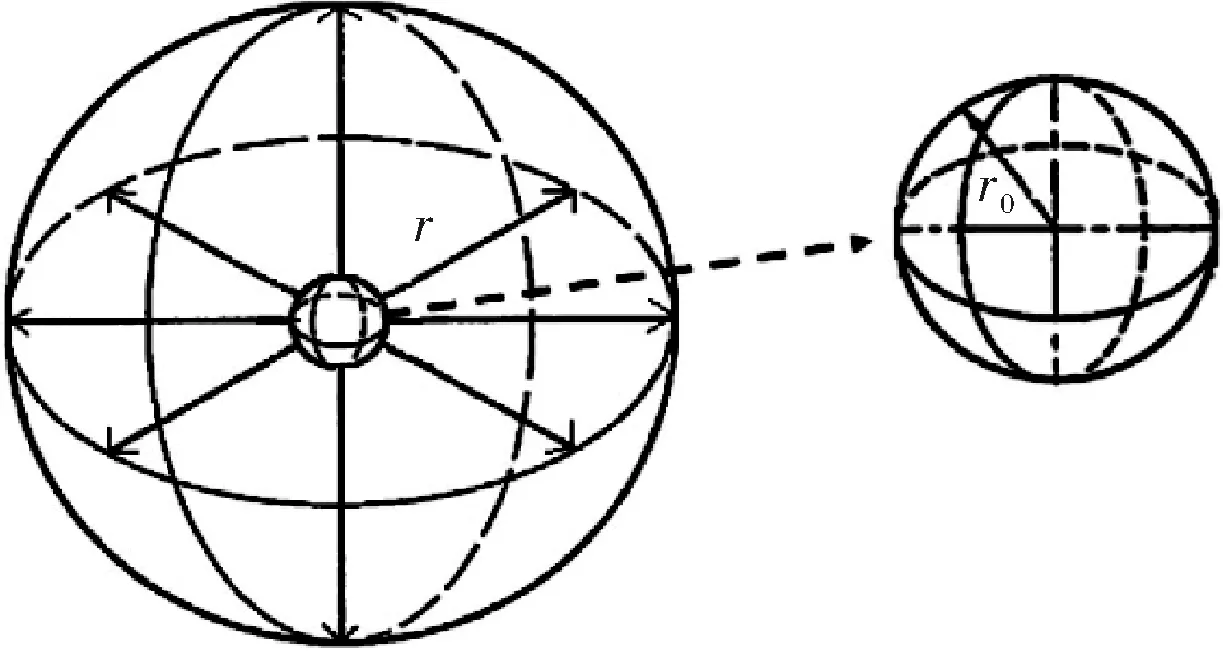
图1 多孔介质的球向渗流示意图[10]Fig.1 The sketch of spherical seepage in porous media[10]
假设多孔介质孔隙分布服从分形分布特征,孔隙的累积数与其大小的分布满足以下的标度关系[1-2]:
(1)
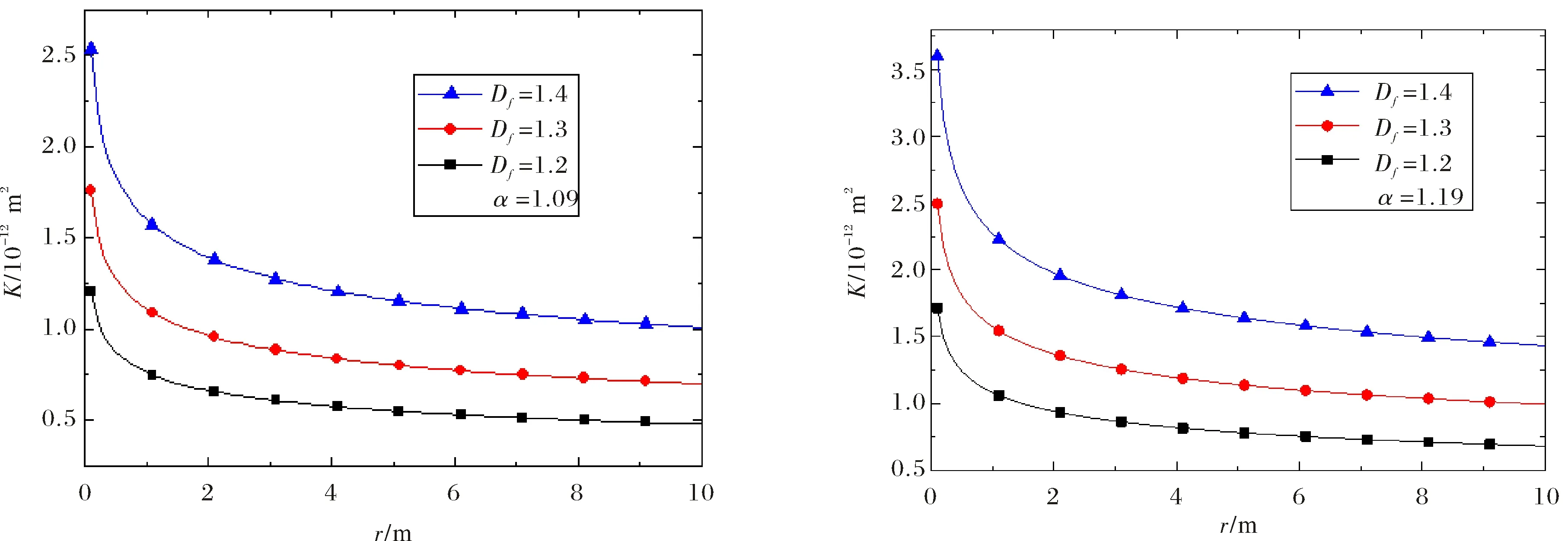
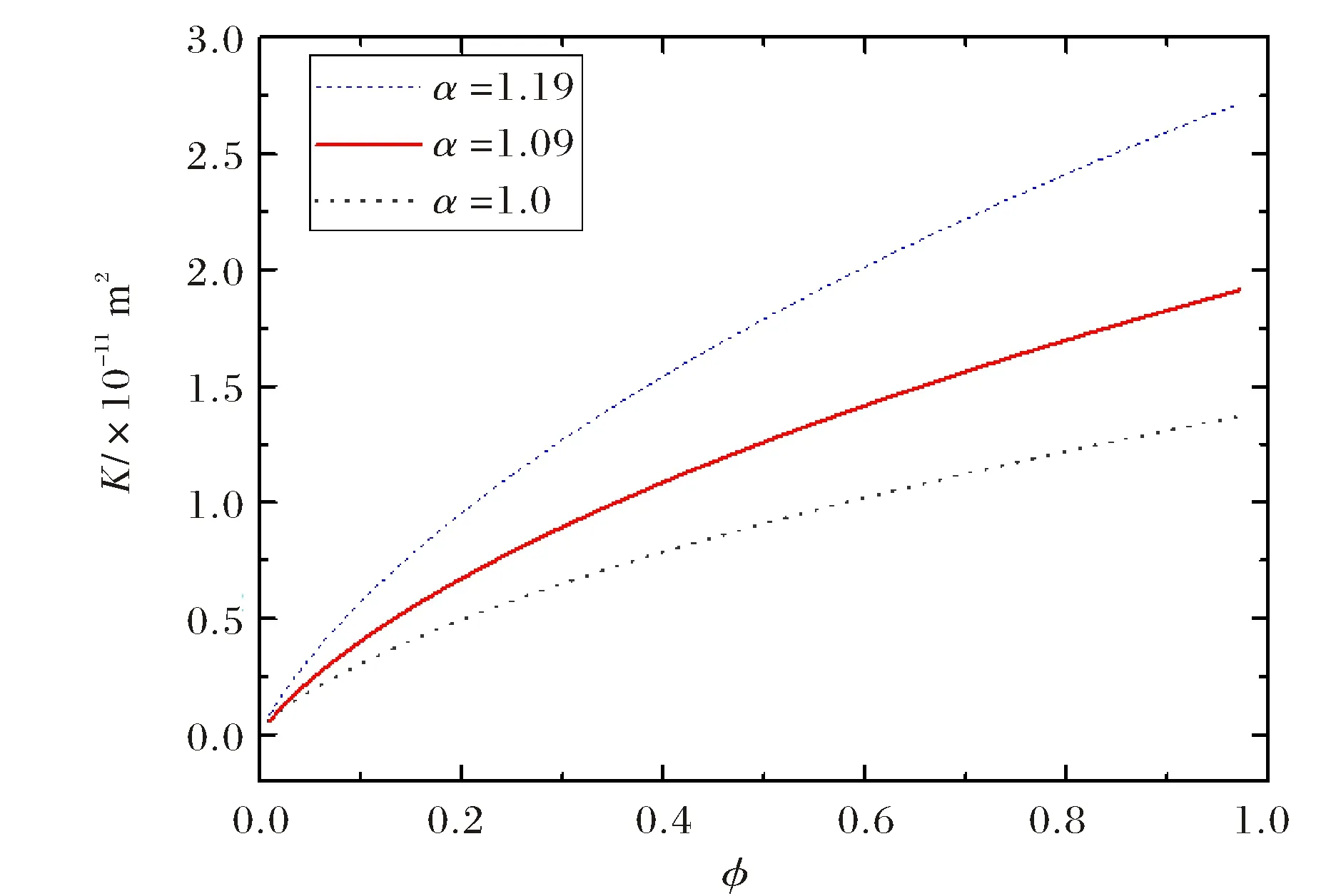
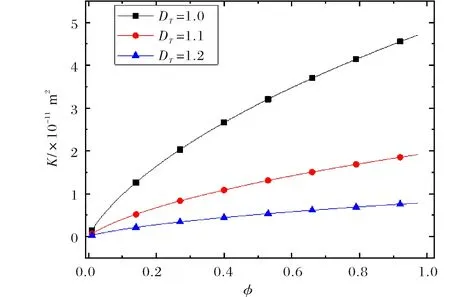
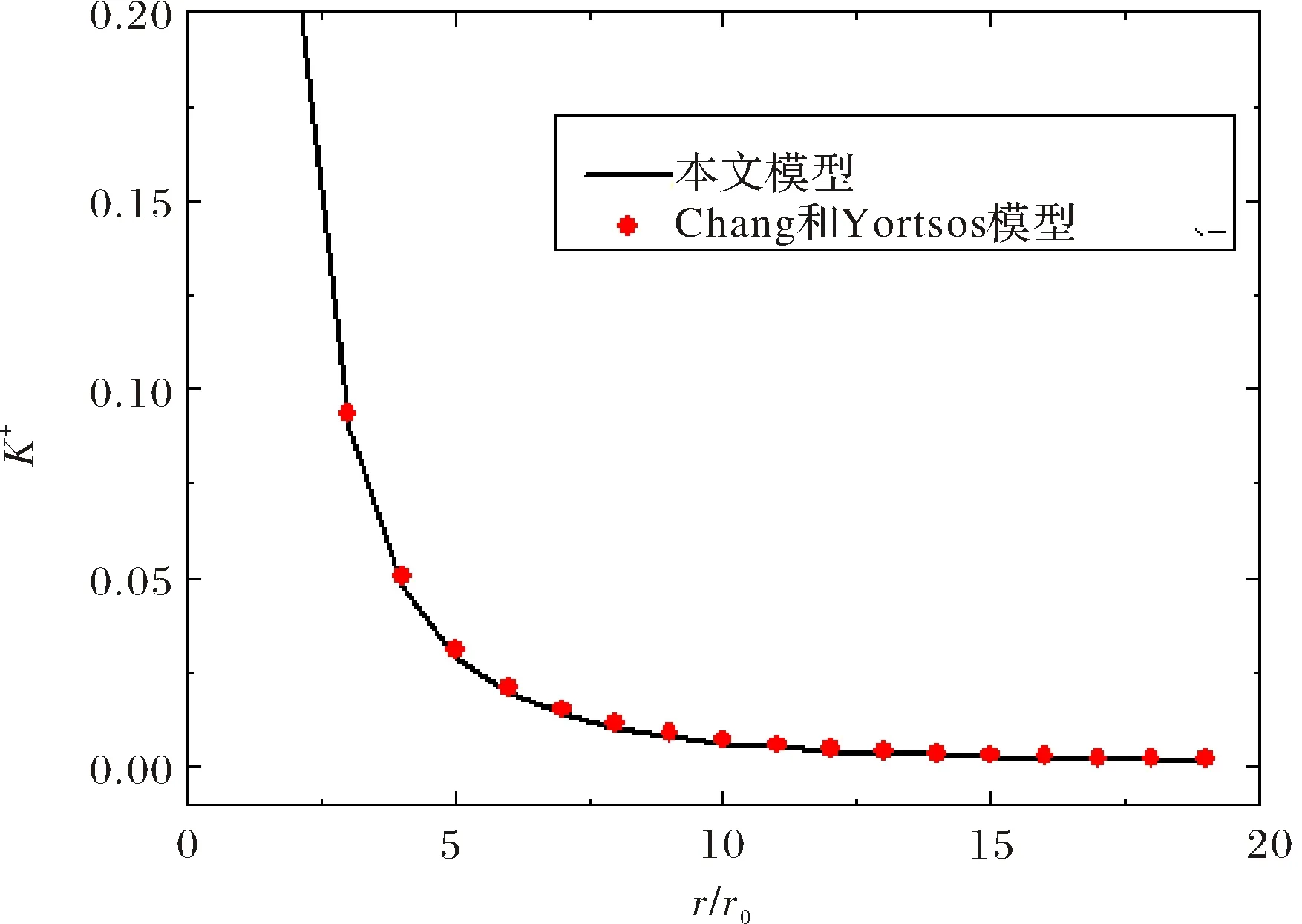
其中,λ为孔隙半径,λmax为最大孔隙半径,Df为孔隙分形维数;一般来说,在二维中0 对(1)式两边微分,得到λ到λ+dλ区间的孔隙数目: (2) 当-dN>0时,则表明孔隙毛细管数目随孔隙尺寸的增大而减少. 多孔介质孔隙总面积为: (3) 根据孔隙率的定义,一个代表性单元面积为: (4) 由哈根-泊松方程可以得到牛顿流体通过水力直径为Dh、横截面为任意形状单根毛细管的体积流量为[11]: (5) 其中,c1是形状因子.对于圆形毛细管c1=1;正方形截面的毛细管c1=1.43;三角形截面的毛细管c1=1.98.Dh为水力直径,其大小由下式给出: (6) 式中,A,C为流动横截面积和湿周长.对于横截面积为非圆形毛细管,假设其等效毛细管直径λ与水力直径Dh成正比,于是将(5)式重新改写,可则得到任意形状毛细管的广义Hagen-Poiseuille方程[11]: (7) 式中,α为毛细管形状因子,根据方程(7),可以确定其值大小:圆形横截面的毛细管α=1;正方形横截面的毛细管α=1.09;三角形横截面的毛细管α=1.19. 由于流体在多孔介质中流动的流线是弯弯曲曲的,所以实际毛细管长度rt大于或等于其直线距离长度r,它们之间满足如下关系[1-3]: rt=rDTλ1-DT. (8) DT是迂曲度分形维数,一般来说其值大于1.大量文献表明多孔介质中毛细管大小分布满足分形标度律,因此,通过横截面面积为Ar=4πr2的球面多孔介质的总流量可以通过下面积分式得到[10]: (9) 将方程(7)和(8)代入(9)式中可得: (10) (11) 根据流体球面径向流动的达西定律: (12) 联立(11)式和(12)式,可以得到球面径向渗透率的表达式: (13) (13)式表明牛顿流体在各向同性多孔介质球向流动时,其渗透率不仅与多孔介质微结构参数(A0,Df,λmax,DT,α)有关,还与径向距离r有关,径向距离越大,渗透率越小.这是因为随着径向距离增大,毛细管占多孔介质横截面的比例越少,导致流动阻力越来越大,最终导致渗透率越来越小.渗透率解析模型(13)式不含任何经验常数,每个参数都有具体的物理意义,能够揭示影响牛顿流体球向渗透率的物理机理,物理意义清晰明确. 当r→r0时,(13)式可以改写成: (14) (14)式表示在井筒壁处多孔介质的球向渗透率.为了得到无量纲化球向渗透率表达式,将(13)式与(14)式相除,得到无量纲渗透率: (15) 通过对式(13)的分析,可以发现球向渗透率是关于α,Df,DT,λmax,A0以及径向距离r的函数,其中A0为代表性单元横截面积的大小,与所选取的多孔介质样品的大小无关,其大小由(4)给出.而孔隙面积分形维数可以由下式确定[1-4]: (16) 最大孔隙直径为[12]: (17) 为了验证本文所提出的球向渗透率模型的正确性,将无量纲渗透率模型(15)式与文献中已有模型作比较.Chang和Yortsos[13]给出了径向流动无量纲渗流模型: (18) 其中,Df代表分形维数,θ为分形网络的谱指数,反映了多孔介质的反常传导性,其值越大,网络的连通性越差,θ的大小一般可以通过蒙特卡洛模拟等数值模拟方法来确定;DE为欧氏空间维数,这里DE=3. 根据方程(13)作出了球向渗透率随径向距离r的变化趋势,如图2(a)和2(b)所示.这里需要说明一点的是,图2(a)与图2(b)分别采用正方形横截面和三角形横截面毛细管.从图2(a)和图2(b)可以看出,球向渗透率随径向距离的增加而逐渐减小,这与物理实际情况一致.另外,也可以发现:球向渗透率随分形维数的增加而增加,即在同一径向半径r处,分形维数越大球向渗透率越大,这也是与实际情况相吻合.因为分形维数越大,说明毛细管所占的份额越大,越有利于流体流动,因此渗透率也就越大. 图2 渗透率随径向距离的变化趋势Fig.2 The radial permeability for spherical seepage in porous media versus the radial distance 图3显示了在井筒壁处半径r0=0.1 m,距离井中心r=5 m处,牛顿流体在由不同横截面毛细管组成的多孔介质中渗流时,球向渗透率随孔隙率的变化.从该图中可以看出,球向渗透率随孔隙率的增加而增加.从该图可以看出,在相同的孔隙率下,由圆形毛细管构成的多孔介质球向渗透率最小,三角形毛细管构成的多孔介质球向渗透率最大,这个结论也可从(12)式得出. 图3 球向有效渗透率随孔隙率的变化Fig.3 The radial permeability for spherical seepage in porous media versus the porosity 图4表明了球向渗透率与迂曲度分形维数之间的变化关系.从图4中可以看出迂曲度分形维数越大,球向渗透率越小.这是因为迂曲度分形维数越大,说明流体流动路径越弯曲,流体所受的流动阻力越大,导致渗透率越小. 为了验证本模型的正确性,图5显示了无量纲球向渗透率模型(15)与已有无量纲球径向渗透率式(18)随径向距离变化趋势.方程(15)中迂曲度分形维数DT=1.2,而Chang和Yortsos[13]给出了径向流动无量纲渗流模型中分形维数Df由方程(16)确定,θ谱指数设为1.784[14].从图5中可以看出:无量纲球向渗透率随径向距离的增加先急剧减小然后缓慢减小最后逐渐趋近于0;本文提出的无量纲渗透率模型与文献Chang和Yortsos的理论模型吻合的很好,验证了多孔介质球向渗透率模型的正确性. 图4 径向渗透率在不同迂曲度分形维数下随孔隙率的变化趋势(参数如下:r0=0.1 m,r=5 m,α=1.09)Fig.4 The radial permeability for spherical seepage in porous media versus the porosity at different tortuosity fractal dimensions at r0=0.1 m,r=5 m and α=1.09. 图5 无量纲渗透率模型与Chang和Yortsos模型的比较 (Φ=0.18)Fig.5 Comparison of the present radial permeability model for spherical seepage in porous media and Chang and Yortsos’s model at Φ=0.18 本文根据分形理论和达西定律,推导了牛顿流体在多孔介质球面径向流动时球向渗透率分形模型.研究结果表明,径向渗透率是分形维数、 孔隙度、 毛细管最小及最大直径、毛细管形状因子的函数,该模型不含经验常数,并且每个参数都有明确的物理意义,揭示了影响球向渗透率的物理机制.通过分析表明球向渗透率随孔隙面积分形维数和孔隙度的增加而增加;随迂曲度分形维数的增加而减小;随径向距离r增加而减少的.这也与实际情况相符合.为了验证该模型的正确性,比较现有模型与已有文献给出的模型,发现两者吻合很好,验证了本文球向渗透率分形模型的正确性.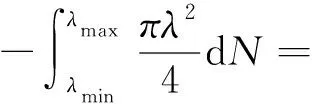
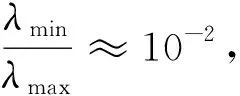
2 结果分析与讨论
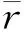
3 结论
