基于性传播疾病的对逼近模型及分析

赵小倩， 秦 鹏， 张菊平

(1.中北大学理学院， 太原 030051； 2.中北大学电气与控制工程学院， 太原 030051；3.山西大学复杂系统研究所， 太原 030051)

性病，全名为性传播疾病，是以性接触为主要传播方式的疾病.国际上将20多种通过性行为或类似性行为引起的感染性疾病列入性病范畴.较常见的性病有淋病、梅毒、非淋菌性尿道炎和艾滋病等.其中，梅毒、淋病和艾滋病等8种性病被列为我国重点防治的性病[1].因此，了解性传染病的传播机理从而制定相应的防控措施非常重要.王燕等[1]研究了一类具有季节性和疫苗接种的SIR传染病模型对控制传染病的影响，揭示了传染病的传播速度小于初始患者为随机分布时的速度；秦文惠等[2]研究了具有一般接触率和用于治疗的SIS对逼近模型及其动力学性质，针对2种菌株是否可以独立生存，建立了一个在规则网络上2种菌株有交叉感染的SIS对逼近传染病模型；李梁晨等[3]的研究，了解病毒在人体内的感染、受制、清除等动力学过程；Carnett[4]针对梅毒提出梅毒螺旋体在易感性伴侣和感染性伴侣接触过程中具有较高的传播可能性.而性伴侣之间的接触形成了一个接触网络，因此，以接触网络为基础构建网络模型来研究性传播疾病会更加切合实际，建立的传染病模型也会更加精确[5-9].对逼近(Pair-Approximation)模型主要研究网络中不同状态的节点及其之间的连边(对或二元组)随时间的变化规律， 是网络传染病模型的一种[10-15].Moris等[16]提出了网络中性伴侣对传染病传播的影响；Ghani[17]探讨了不同网络方法在性病流行病学中的作用；Bauch[18]探索了网络中对逼近在研究性病过程中的应用；Kim[19]讨论了在性传播过程中传播率在男性对女性和女性对男性之间可能不同；Miller等[20]给出了传染病在网络传播中已有的方法和当前面临的挑战[21].本文主要基于接触网络建立异性恋中性病传播的SIS对模型，并对其进行分析.

1 模型的建立

假设网络中的总人口数为N，分别用m和f表示异性恋接触网络中的男性和女性，女性总人口为Nf(t)，男性总人口为Nm(t)，从而有N(t)=Nf(t)+Nm(t).将人群分为易感者(S)和染病者(I)，分别用Sf(或Sm)和If(或Im)表示女性(或男性)易感者和染病者，[Sf(t)](或[Sm(t)])和[If(t)](或[Im(t)])表示t时刻女性(或男性)易感者和染病者的数量.[AB]表示A-B连边的数量，[ABC]表示A-B-C三元组的数量，其中A，B，C∈{Sf，Sm，If，Im}.接触网络上异性恋的性病传播流程图如图1所示.

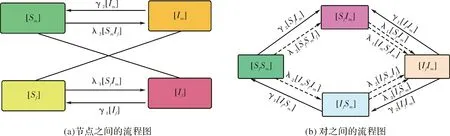
图1 接触网络上异性恋的性病传播流程图Fig.1 Flow chart of STD transmission on the heterosexual network

根据图1建立网络上异性恋的性传播SIS对逼近动力学模型为:

(1)

其中，λ1(λ2)表示易感者女性(男性)与染病者男性(女性)接触的传染率，γ1(γ2)表示女性(男性)染病者的恢复率.

因为

所以N(Nf，Nm)为常数.假设节点的染病者邻居服从二项分布，有逼近公式[10]：

(2)

其中A，B，C∈{Sf，Sm，If，Im}.

由异性网的平衡条件有

nmNm=nfNf，

[SfSm]+[SfIm]+[SmIf]+[ImIf]=nfNf.

(3)

将(2)、(3)代入模型(1)，得到如下系统:

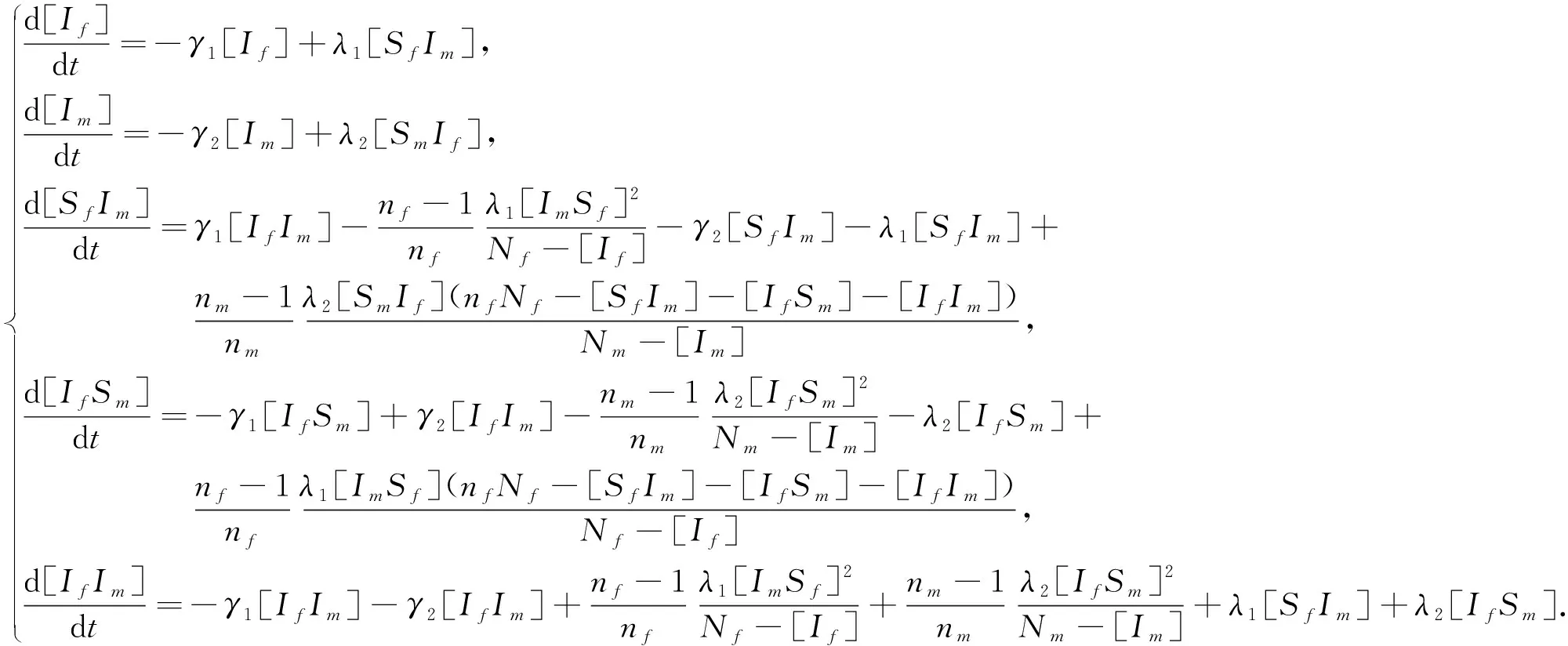
(4)

容易证得系统(4)正向不变集为

0≤[Im]+[If]≤N，

0≤[SfIm]+[IfSm]+[IfIm]≤nfNf}.

2 无病平衡点和基本再生数

系统(4)有无病平衡点E0=(0，0，0，0，0)，它在E0处的雅可比矩阵JE0为

(5)

计算得(5)的特征方程为

(τ+γ1)(τ+γ2)(τ3+τ2a1+τa2+a3)=0，

其中，

a1=2γ1+2γ2+λ1+λ2，

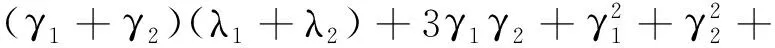
λ1λ2nf+λ1λ2nm-λ1λ2nfnm，

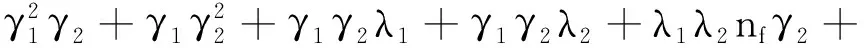
λ1λ2nmγ1-λ1λ2nfnm(γ1+γ2).

特征方程有两个特征根为-γ1和-γ2，其余特征根满足

τ3+τ2a1+τa2+a3=0.

(6)

由Hurwitz判据知，当H1>0，H2>0，H3>0时，雅可比矩阵的所有特征根均具有负实部，则系统(4)的零解局部渐近稳定，其中，

H1=a1>0，

H2=3(λ1+λ2)(γ1+γ2)2+

(γ1+γ2)((7γ1γ2+(λ1λ2)2))+

γ1λ1λ2(nm+2nf)+λ1λ2(nf+nm)(λ1+λ2)-

λ1λ2nfnm(λ1+λ2+γ1+γ2)，

H3=(γ1γ2(λ1+λ2+γ1+γ2)+

λ1λ2(γ2nf+γ1nm)-(γ1+γ2)λ1λ2nfnm)H2.

要使H2>0，H3>0，只需H2>0，a3>0，即

其中，

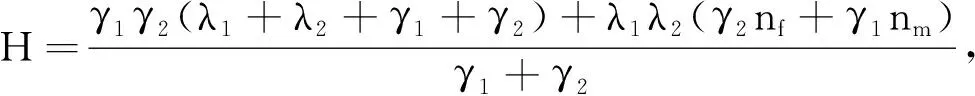
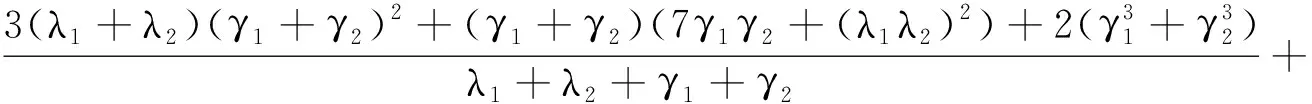
因为M>H，故只需满足

定理1当R0<1时，系统(4)的零解是局部渐近稳定的，当R0>1时不稳定.

3 正平衡点的存在性

下面讨论系统(4)正平衡点的存在情况.

令系统(4)后4个方程的右端为零，可得

(7)

将(7)代入系统(4)第5个方程的右端令其为零，可得关于[If]的一元二次方程:

P[If]2+Q[If]+W=0.

(8)

其中，

a=γ1+nfλ1，b=γ2+nmλ2，

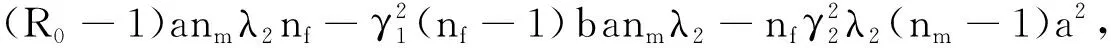
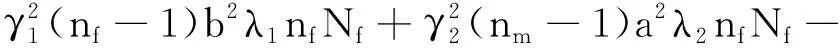
(R0-1)(nfλ1b+nmλ2a)nfNf，

方程(8)判别式为

Δ=(R0-1)2(A-B)2+

2(R0-1)(A-B)(C-D)+(C+D)2.

(9)

其中，

A=nfλ1b，B=nmλ2a，

将方程(9)看成Δ关于R0-1的一元二次函数，求函数的最低点为

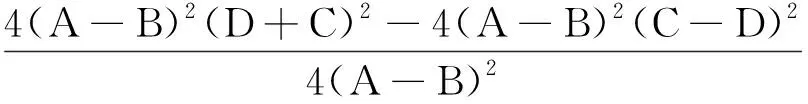
4DC>0.

下面分情况讨论一元二次方程(8)根的存在性.

1)当R0>1时，有W>0.

(1) 当P<0且Q>0时，若满足

(2) 当P<0且Q≤0时，若满足

(3) 当P>0且Q<0时，若满足

方程(8)有两个正根，则系统(4)有两个正平衡点，

和

其中，

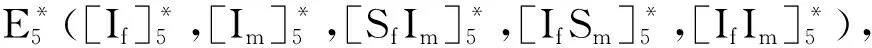
3)当R0<1时，有W<0.

当P<0，Q>0时，方程(8)有两个正根，则系统(4)有两个正平衡点，

和

其中，

因此，总结如下表1所示.

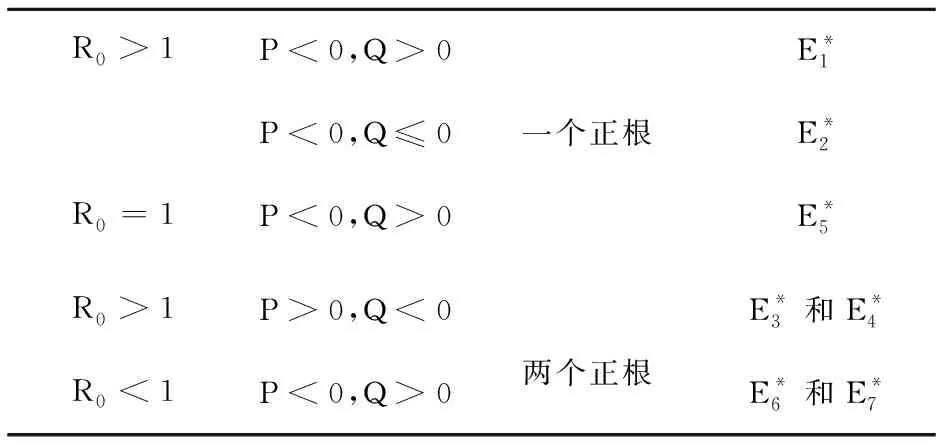
表1 正平衡点的存在性

4 数值模拟

下面通过数值模拟验证理论分析的正确性.取

Nf=80，Nm=60，nf=3，nm=4，

γ1=0.44，γ2=0.1，λ1=0.08，λ2=0.09，

则有R0>1，P<0，Q>0，系统(4)存在唯一的正平衡点且是稳定的(见图2).

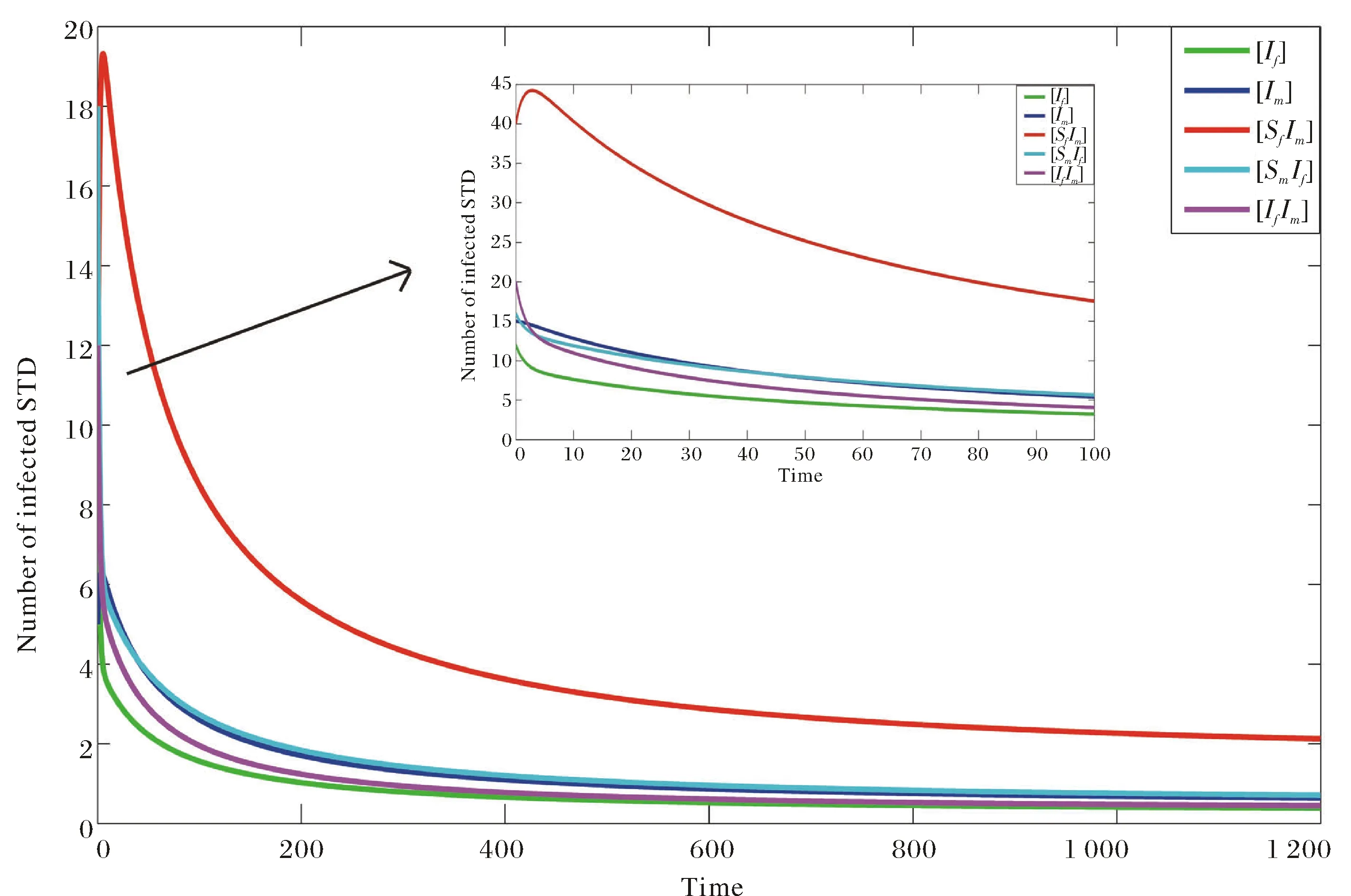
图2 R0>1，P<0，Q>0时的时间序列图Fig.2 Time series diagram，when R0>1，P<0，Q>0

取

Nf=80，Nm=60，nf=3，nm=4，

γ1=0.42，γ2=0.1，λ1=0.08，λ2=0.09，

则有R0>1，P<0，Q<0，系统(4)存在唯一的正平衡点且是稳定的(见图3).

取

Nf=80，Nm=60，nf=3，nm=4，

γ1=0.1，γ2=0.15，λ1=0.06，λ2=0.07，

则有R0>1，P>0，Q<0(用实线表示).在参数不变，当Nf=40，Nm=30时(用虚线表示) (见图4).

进一步给出了R0关于参数γ1对[If]的影响(见图5).

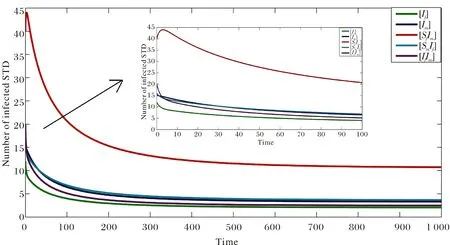
图3 R0>1，P<0，Q<0时的时间序列图Fig.3 Time series diagram， when R0>1，P<0，Q<0

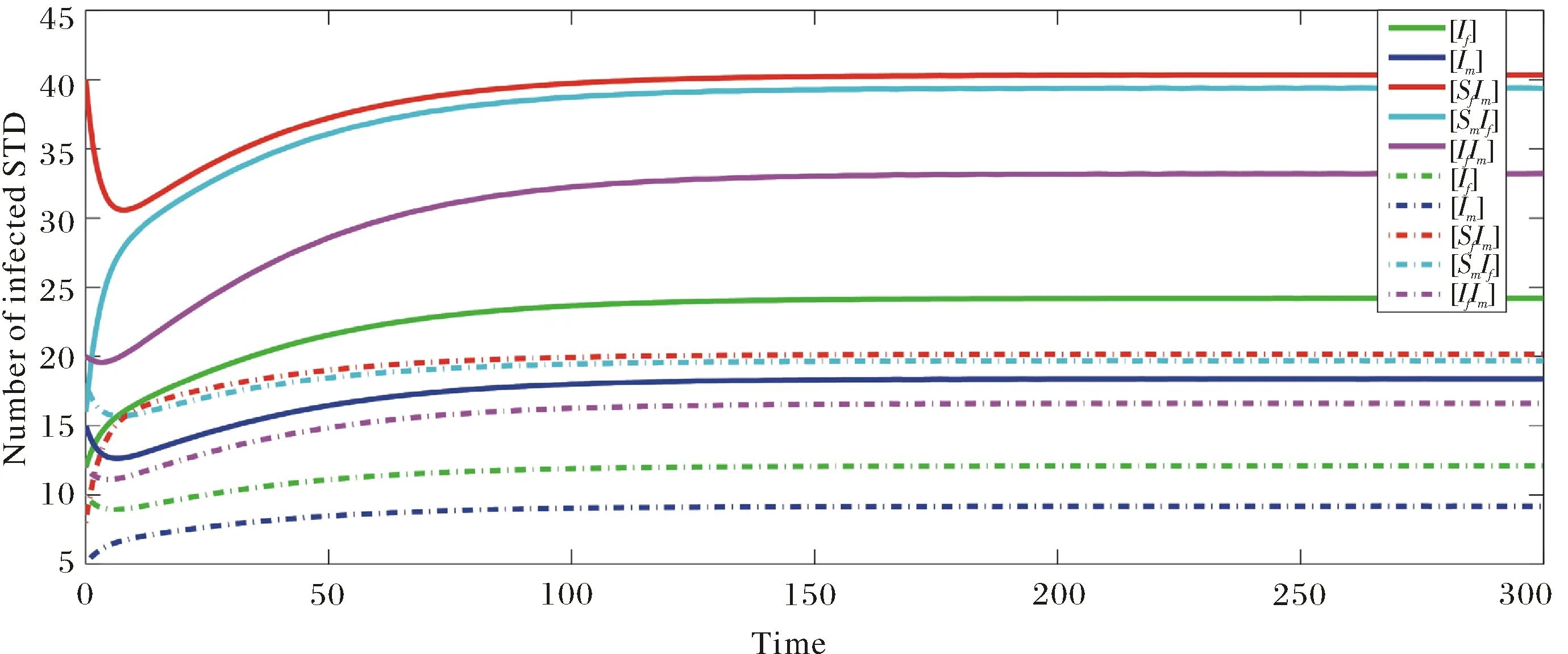
图4 R0>1， P>0，Q<0时的时间序列图Fig.4 Time series diagram，when R0>1， P>0，Q<0

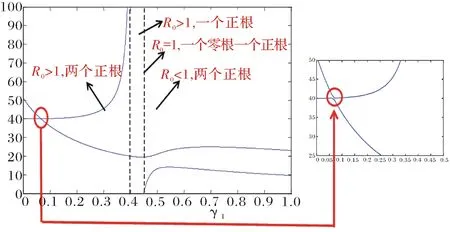
图5 γ1对[If]的影响Fig.5 γ1impact on[If]

5 结论

本文用网络对逼近传染病模型来研究异性恋之间的传染病，建立了静态网络上性传播疾病的SIS对逼近传染病模型.通过理论分析证明了无病平衡点的存在性及其局部稳定性，得到了基本再生数R0.当R0<1时无病平衡点局部渐近稳定，当R0>1时无病平衡点不稳定.分情形讨论了正平衡点的存在性，并通过数值模拟验证了理论结果的正确性.