螺旋锥齿轮润滑试验相似模型及影响因素

王延忠 杨凯† 齐荣华 唐文

(1.北京航空航天大学 机械工程及自动化学院，北京 100191；2.中国电子科技集团公司第三研究所，北京 100015)

航空齿轮是航空发动机动力传输的重要部件，其润滑性能的优劣对其抗胶合、抗磨损能力有直接影响。随着弹流润滑理论的发展，目前对齿轮润滑的理论研究已初步形成体系。杨沛然等[1- 2]根据直齿和斜齿圆柱齿轮的特点，考虑了瞬态效应、表面温度场等因素，利用多重网格技术对齿轮不同啮合点的润滑油膜厚度和压力分布进行了数值求解；Castro、Evans等[3- 4]结合齿轮的微观形貌，对混合润滑状态下的齿轮润滑特性和疲劳破坏进行了计算；Simon[5]利用齿面加载接触分析技术，计算分析了啮合区几何参数对螺旋锥齿轮润滑性能的影响。这些理论和计算方法为齿轮润滑设计时齿面修形、供油参数、润滑油物理参数的合理选择提供了有效的手段。Pu等[6- 7]基于混合润滑分析模型，研究了不同速度方向对椭圆接触混合润滑状态的影响，实现了对接触区摩擦系数以及温度场分布的分析，该模型可以进一步应用在螺旋锥齿轮的润滑和热特性分析中。

齿轮润滑油膜的测量方法主要有电阻法、电容法、放电电压法、阻容振荡法等，但这些方法测量精度较低，只能实现定性测量，无法精确测得接触区的油膜分布情况，而且标定困难。目前对于微纳米级的润滑油膜测量，比较成熟的方法为光干涉法和电压电容法[8- 9]。光干涉法使用光干涉原理，需要使用钢球和透明玻璃盘作为试验对象，其工作载荷和测量尺寸都较小；电压电容法受润滑油、清洁度、表面粗糙度影响较大，测量误差大，无法直接应用在齿轮的润滑膜厚测试中。新兴的超声波测量油膜厚度的方法[10- 11]受限于换能器的制造频率只能测试较厚的油膜，而且误差较大，需要通过不断标定来修真测试结果，无法在齿轮的润滑油膜测试中直接应用。

为了实现螺旋锥齿轮润滑特性的测试，本研究提出一种基于相似性理论[12]的试验方法。首先将螺旋锥齿轮两齿的啮合过程用若干个当量曲率曲面和一个平面的接触来代替，使其初步具备在光干涉试验台上进行试验的几何特征；然后利用相似理论对原系统进行相似缩小，使其满足试验台的载荷和尺寸测量范围，提出用轻载、低速、小尺寸的齿轮相似润滑试验反映真实尺寸齿轮润滑特性的方法；最后分析了各主要参数对系统相似程度的影响。

1 螺旋锥齿轮接触区当量曲率球几何及运动参数计算

1.1 接触区当量曲率球几何计算

根据螺旋锥齿轮的加载接触分析结果[13]，提取载荷作用下的接触点位置以及大轮和小轮在接触点的相对法曲率ΔA、ΔB和相对短程挠率ΔC以及切平面内的接触椭圆长轴、短轴的空间单位向量η、ζ。将螺旋锥齿轮的啮合过程简化为当量曲率球与平面接触，其当量曲率球的最大主曲率ΔKmax和最小主曲率ΔKmin可以由式(1)求得[14]：

(1)

式中：对于大轮凹面、小轮凸面的传动，符号±使用+；对于大轮凸面、小轮凹面的传动，符号±使用-。

在啮合切平面中，若令坐标系x方向与接触椭圆短轴重合，则x方向的曲率半径Rx=1/ΔKmax，y方向的曲率半径Ry=1/ΔKmin。

1.2 啮合接触区卷吸速度计算

螺旋锥齿轮的加载接触分析的结果表明[13]，啮合中点位置的载荷最大、油膜压力最大，最具代表性。本研究以啮合中点位置为基准，对螺旋锥齿轮的啮合点速度、卷吸速度、油膜厚度展开分析。

将螺旋锥齿轮的接触问题简化为当量曲率球与平面的二维点接触问题后，需要将啮合点处大轮齿面的速度v1和小轮齿面的速度v2投影到切平面内进行卷吸速度的求解。图1中T为接触点M的切平面，x、y为接触椭圆短轴和长轴的方向，u1、u2为v1、v2在切平面T中的投影，u为u1与u2的矢量和。

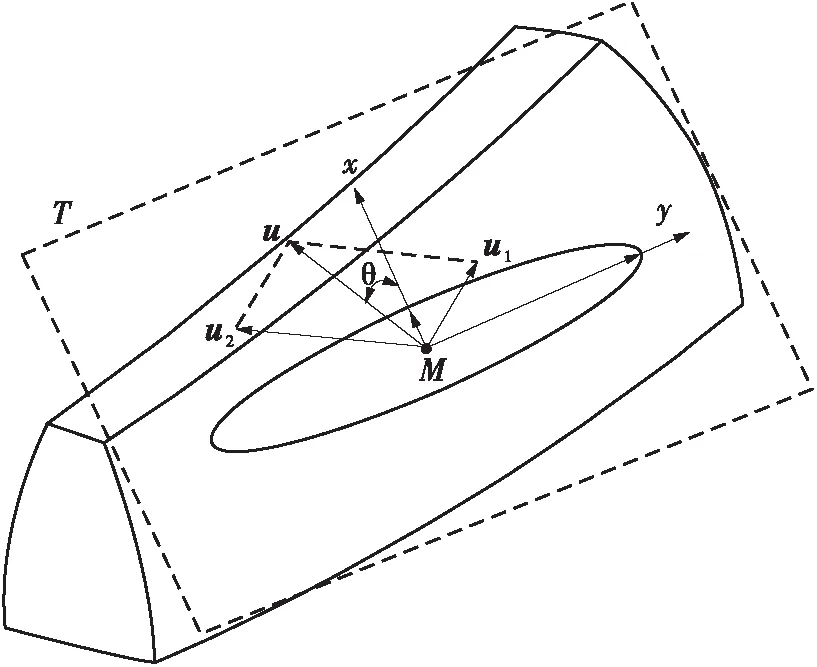
图1 接触区卷吸速度的计算模型

Fig.1 Calculation model of the entrainment speed in the contact area

将u1和u2在接触椭圆短轴x和长轴y方向进行投影，分别得到u1ζ、u1η和u2ζ、u2η，其中矢量和u与接触椭圆短轴x方向的夹角为θ，如图2所示。

u1在y、x方向上的投影为

u1η=v1·η

(2)

u1ζ=v1·ζ

(3)

u2在y、x方向上的投影为

u2η=v2·η

(4)

u2ζ=v2·ζ

(5)

则卷吸速度um为

(6)

卷吸速度um的大小um为

(7)

卷吸速度um与接触椭圆短轴x方向的夹角θ：

(8)

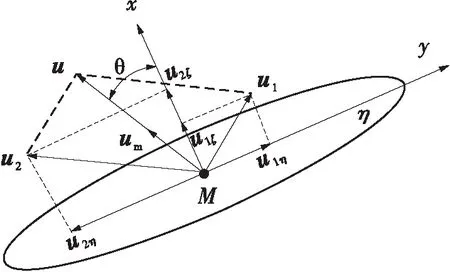
图2 接触区卷吸速度投影图

Fig.2Projection graph of the entrainment speed in the contact area

2 点接触润滑相似模型的建立

2.1 确定量纲系统和主要参数

点接触弹流润滑问题为典型的力系统，根据量纲系统的转换法则[8]，以力、长度、时间为基本量纲，用符号可以表示为FLT系统。其中，F为力量纲、L为长度量纲、T为时间量纲。

根据等温点接触弹流润滑中考虑的参数[15- 16]，将点接触弹流润滑系统的主要参数确定为7个：接触点载荷w、卷吸速度u、润滑油环境粘度η0、润滑油粘压系数α、接触点的当量曲率半径R、当量弹性模量E以及油膜厚度h。这7个独立物理量的单位及其量纲表示形式如表1所示。

表1接触弹流润滑系统的主要参数

Table1Main parameters of point contact elastohydrodynamic lubrication system

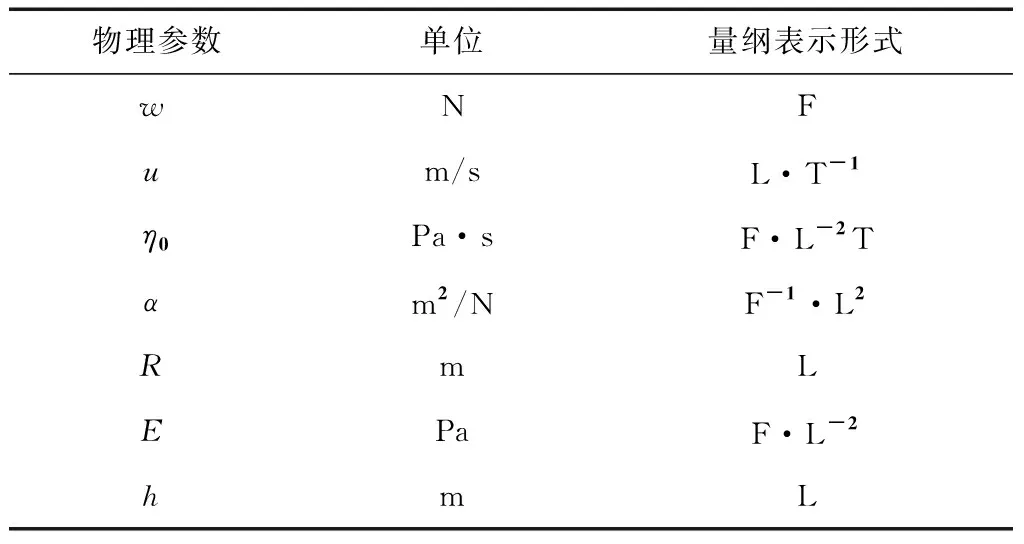
物理参数单位量纲表示形式wNFum/sL·T-1η0Pa·sF·L-2Tαm2/NF-1·L2RmLEPaF·L-2hmL

2.2 根据量纲矩阵建立系统的相似准则

将表1的7个物理参数作为行，系统的基本量纲作为列，建立系统的量纲矩阵，并使用a1、a2、…、a7分别代表参数u、h、η0、R、E、w、α，如式(9)所示：

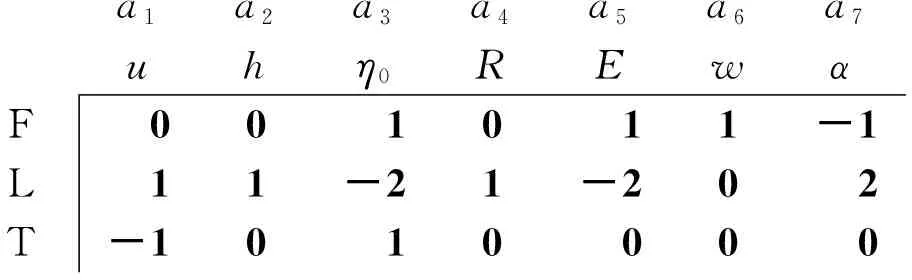
a1a2a3a4a5a6a7uhη0REwαFLT 00 10 11-1 11-21-20 2-10 10 00 0

(9)

相似准则的数目可由参数的数量减去量纲矩阵的秩得到[12]。此矩阵的秩为3，参数数量为7，可知相似准则数目为7-3=4个。按此矩阵可以分别写出以u、η0、h表示的R、E、w、α，这4个关系式即为系统的相似准则。

用u、η0、h表示R：

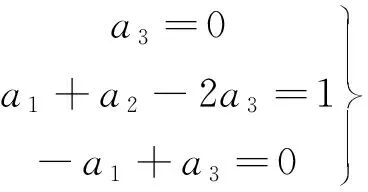
(10)

用u、η0、h表示E：

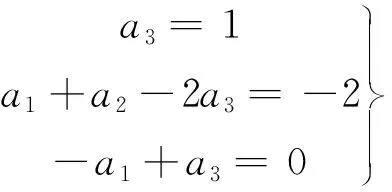
(11)

用u、η0、h表示w：

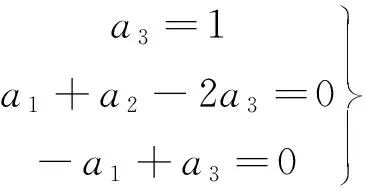
(12)

用u、η0、h表示α：

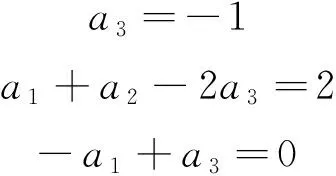
(13)

综上可得系统的4个相似准则为

(14)

利用这个相似模型，通过改变载荷、速度、几何和润滑介质参数，利用光干涉试验台间接测量齿轮接触区的润滑油膜厚度。由于螺旋锥齿轮的卷吸速度方向与接触椭圆短轴有一定夹角，试验时需根据计算方向设置椭圆钢球与玻璃盘旋转切线方向的相对位置。

3 相似模型的理论验证及各参数对系统相似程度的影响

3.1 利用弹流润滑理论计算润滑油膜厚度

根据椭圆接触弹流润滑理论，采用Venner的点接触弹流润滑基本方程[14]，求解螺旋锥齿轮弹流润滑下的油膜厚度和压力分布。

(1)Reynolds方程

(15)

式中：p为油膜压力；h为油膜厚度；ρ为润滑油密度；η为润滑油黏度；um为卷吸速度。

(2)油膜几何方程

(16)

式中，Rx、Ry为x、y方向的曲率半径。

(3)油的黏度方程

采用Roelands关系求解

η(p)=η0exp(lnη0+9.67)·

(17)

式中，η0为大气压下润滑油黏度，z取0.68，p0取1.96×108。

(4)润滑油的密度方程

(18)

式中，ρ0为大气压下润滑油密度。

(5)载荷平衡方程

(19)

式中，w为接触点载荷。

根据方程(15)-(19)，参考Venner和Lubrecht的多重网格法[10]，编制弹流润滑数值计算程序，计算等温点接触润滑接触区的润滑油膜厚度和压力分布。

以某型航空发动机主减螺旋锥齿轮为例，进行弹流润滑油膜厚度计算，并进行润滑相似性影响分析。主减螺旋锥齿轮工作功率450kW，工作转速6000r/min，其它基本设计参数如表2所示。

表2算例齿轮基本参数

Table2Basic parameters of the gear in the example

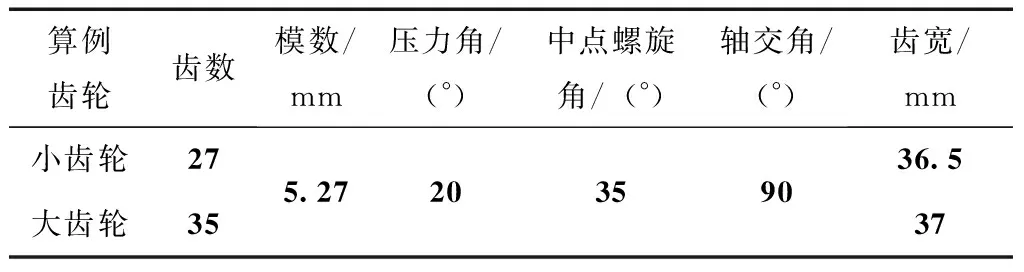
算例齿轮齿数模数/mm压力角/(°)中点螺旋角/(°)轴交角/(°)齿宽/mm小齿轮27大齿轮355.2720359036.537

根据式(1)-(8)，可以得到螺旋锥齿轮某一时刻啮合区的载荷、当量曲率半径、卷吸速度参数(具体数值见表3)；再由弹流润滑数值计算程序可计算出接触区的油膜厚度和压力分布，如图3、图4所示。

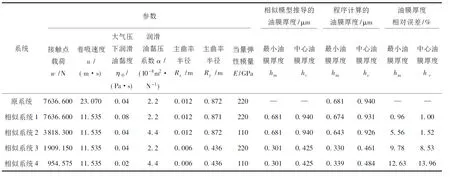
表3 相似系统参数及结果比较

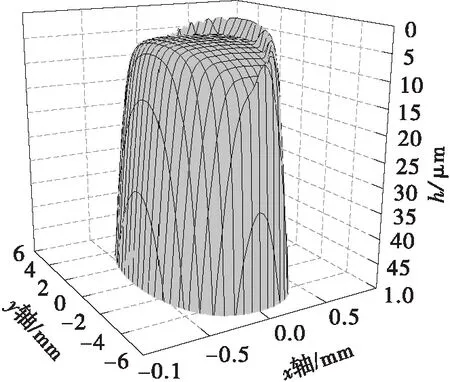
图3 接触区油膜厚度分布计算结果

Fig.3Calculation results of oil film thickness distribution in contact area

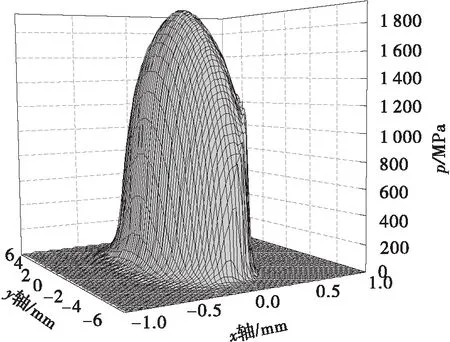
图4 接触区压力分布计算结果

Fig.4Calculation results of pressure distribution in contact area

3.2 不同参数对系统相似程度的影响

根据点接触润滑相似模型，以算例参数为原系统，建立4个不同参数的相似系统，如表3所示。利用点接触弹流润滑计算程序，分别计算各相似系统的中心油膜厚度和最小油膜厚度，并与用相似模型推导的膜厚相比较，分析各物理参数的变化对系统相似程度的影响。

表3中“相似模型”中的膜厚由相似模型得到，“程序计算”中的膜厚由弹流润滑数值计算程序获得。相对误差计算方法为：

(程序计算的膜厚-相似模型的膜厚)/程序计算的膜厚×100%。

从表3中最小油膜厚度和中心油膜厚度的误差比较可以看出：

相似系统1的相对误差为0.96%和1.00%，误差几乎可以忽略，说明只改变卷吸速度和润滑油粘度对系统的相似程度影响很小，几乎可以做到完全相似。

相似系统2的相对误差为5.56%和1.52%，说明改变载荷和粘压系数对相似系统有一定的影响，这主要是因为润滑油黏度与压力的非线性关系。

相似系统3的误差为9.78%和8.53%，说明同时改变载荷、卷吸速度、润滑油黏度和曲率半径对系统相似程度影响变大，有叠加效果。

相似系统4的相对误差为12.63%和13.96%，此时系统的载荷、卷吸速度、润滑油黏度、黏压系数、曲率半径和弹性模量同时发生了改变，说明单独因素的影响较小，变量增多时，系统的相对误差变大。误差叠加效应显著。

4 实验数据验证

在传统的齿轮润滑试验中，可通过提高润滑油的黏度，降低卷吸速度，保证卷吸速度与润滑油黏度的乘积不变，再将卷吸速度转化为对应的测试转速，用降低的测试转速进行试验，达到用低速工况对高速工况进行相似试验的目的。

宋炳坤[17]对点接触混合润滑油膜厚度进行了大量的实验研究，对不同黏度润滑剂在不同卷吸速度下的油膜厚度测量符合本研究相似系统1的要求；这里引用文献[17]的实验数据和相似系统进行对比分析(试验测试中仅仅是对润滑油黏度和卷吸速度进行了改变，试验中使用的是同一组石英玻璃盘和钢球，在相同的环境和温度下进行。即保持曲率半径、弹性模量和黏压系数不变)，引用的数据如表4所示，结果对比如表5所示。

从表5对工况1-6油膜厚度的实验结果与相似模型结果的对比表明：在保持卷吸速度与润滑油黏度乘积不变的情况下，降低润滑油黏度、增大卷吸速度，实际油膜厚度与相似模型结果最大相对误差12.82%，模型有效。但工况6显示，当进一步降低润滑油黏度提高卷吸速度时，实验结果与相似模型结果相差较大，达到35.00%。这主要是因为此时的卷吸速度变化较大，文中的模型中没有考虑润滑油的黏温特性，卷吸速度大幅变化时，弹流润滑过程发热量差异大，导致模型失效。

表4 不同工况下的油膜基本参数

表5油膜厚度的实验结果与相似模型结果对比表

Table5Comparison of experimental results and similarity model results of oil film thickness

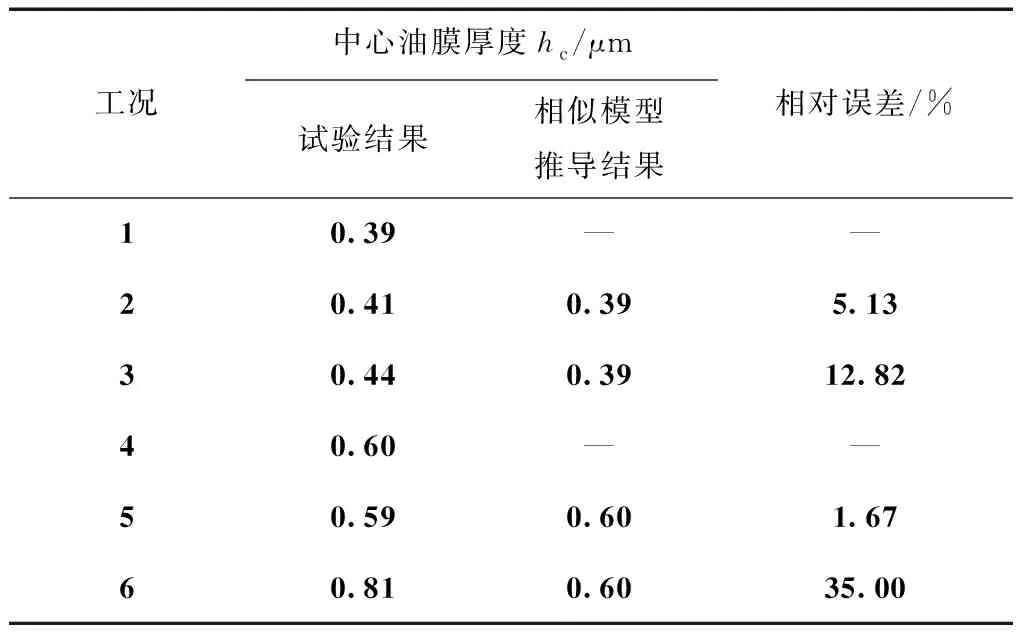
工况中心油膜厚度hc/μm试验结果相似模型推导结果相对误差/%10.39——20.410.395.1330.440.3912.8240.60——50.590.601.6760.810.6035.00

5 结论

(1)螺旋锥齿轮的润滑问题可以抽象为当量曲率球与平面的点接触润滑问题。在确保相似准则不变的前提下，仅改变卷吸速度和润滑油黏度对系统相似程度几乎没有影响；改变载荷、黏压系数、曲率半径和弹性模量时，系统相似误差变大；改变的参数越多，误差叠加效应越明显。

(2)根据相似试验模型合理选择参数，可在光干涉膜厚试验台上用低速、轻载的参数，间接测量螺旋锥齿轮接触区的油膜厚度，也可在传统的润滑试验中用低速试验代替高速试验。

(3)试验数据与相似模型结果比较表明，卷吸速度小于1m/s时，相似模型结果与实验结果比较接近，最大误差12.82%；当卷吸速度变化较大时(原模型u=0.56m/s，相似模型u=2m/s)，相似模型结果偏差较大。这主要是因为文中的模型中没有考虑润滑油的黏温特性，卷吸速度的大幅变化使得接触区油膜温度发生改变，影响了润滑油黏度，导致模型失效。