CCFD中继系统中基于多维矩阵的信道估计方法
2020-02-12韩曦周迎春赵欣远白文乐
韩曦 周迎春 赵欣远 白文乐
(北方工业大学 信息学院,北京 100144)
在无线通信系统中,协同分集技术已经成为高速传输的重要解决方案,与传统的点对点通信系统相比,该技术提高了容量和覆盖范围;其中,放大转发(Amplify and Forward,AF)中继方案由于执行简单、无需解码等优点而被广泛应用[1]。同时同频全双工(Co-time Co-frequency Full Duplex,CCFD)无线通信设备使用相同的时间、相同的频率,同时发射和接收无线信号。AF中继与CCFD技术相结合,能充分利用空间分集,进一步提高系统性能。理论上,CCFD将无线链路的频谱效率提高了一倍,并且可以减少端到端的时延和信令开销,已成为5G技术的研究热点[2]。但应用中,由于发送和接收的信号可以同时在相同频率下被检测到,接收端产生严重的自干扰,这将增加系统接收和检测信号的难度。因此,在接收信号之前需要有效地削弱自干扰,获得准确可靠的信道状态信息(Channel State Information,CSI)。
在多输入多输出(Multiple Input Multiple Output,MIMO)中继系统中,文献[3]提出了一种两步训练(Two-Stage Training,TST)信道估计方法,但其第二跳信道矩阵的估计结果受第一跳估计结果的影响。文献[4]在双向中继系统中提出了两种信道估计算法,但并未考虑CCFD双工通信带来的干扰和对估计性能的影响。文献[5]在MIMO中继系统中,提出了一种非迭代P_KRF(PARAFAC with Khatri-Rao Factorization)信道估计方法,该方法降低了计算复杂度,具有良好的信道估计性能。
为了降低自干扰对CCFD系统的影响,获得准确的CSI,文中提出了一种基于多维矩阵的直接求解算法,该算法无须迭代,利用多维矩阵的低秩分解即可求得CSI,适用于更灵活的天线配置;最后通过仿真对所提算法的有效性进行了验证,并与最小二乘(Least Square,LS)、TST和非迭代P_KRF信道估计方法进行了对比。
1 系统模型
1.1 全双工模型
在图1所示的双向CCFD AF中继系统中,用户1和用户2分别配置M1和M2根天线,R个中继分别配有N1、N2、…、NR根天线,设两用户在中继两侧对称分布,中继天线数量MR=N1+N2+…+NR。用户之间通过中继传递信息,整个传输过程可分为两个阶段:第一阶段,用户1和用户2将信号发送给中继;第二阶段,中继对接收的信号进行自干扰消除,然后放大转发至两用户,并同时接收来自用户1和用户2的信号。

图1 系统模型框图
1.2 数据模型
用户I发送的信号矢量为xI∈CMI×1,其中I=1,2;用户I与中继之间的信道矩阵为HIR∈CMR×MI,HRI∈CMI×MR表示相反方向的信道矩阵;假设信道具有互易性,即HRI=(HIR)T[6]。用户I端自干扰信道矩阵为HII∈CMI×MI,中继到中继环路的自干扰信道矩阵为HRR∈CMR×MR;中继与用户I接收的噪声矢量分别为nR∈CMR×1、nRI∈CMI×1。中继接收的信号矢量为r∈CMR×1,对信号的放大矩阵为G∈CMR×MR,转发的信号矢量为xR∈CMR×1。用户I接收的信号矢量为yI∈CMI×1。
第一阶段t时刻时,中继接收的信号可表示为
r(t)=H1Rx1(t)+H2Rx2(t)+HRRxR(t)+
nR(t)
(1)
1.2.1 中继节点的自干扰消除
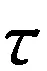
(2)
将式(1)带入式(2),可得

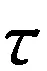
(3)
当上式满足自干扰抑制条件GHRRG=0时[7],式(3)为
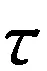
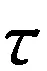
(4)
1.2.2 用户端的自干扰消除
第二阶段,两用户接收的信号分别为
(5)
目的节点的自干扰可通过外部物理电路消除。如图2所示,消除幅度可达20~30 dB[8]。经过自干扰处理后,两用户接收的信号简化为
(6)
根据式(4)和(6),可得
(7)


图2 基于自适应滤波器消除自干扰示意图
Fig.2 Schematic diagram of self-interference cancellation based on adaptive filter
1.3 PARAFAC模型
1.3.1 基本运算
三维PARAFAC分解展开式[9]分别为
{[I3,S×1A×2B×3C](1)=A(B⊙C)T
[I3,S×1A×2B×3C](2)=B(C⊙A)T
[I3,S×1A×2B×3C](3)=C(A⊙B)T
(8)
其中:I3,S表示维度为S×S×S的三维矩阵;A∈CP×S;B∈CQ×S;C∈CR×S;符号⊙表示Khatri-Rao乘积;×n表示模式n积,n=1,2,3。
1.3.2 多维矩阵建模
为了获得准确的CSI,两用户分别发送导频序列x1,j、x2,j[10],j=1,2,…,NP。定义[11]
(9)
其中:多维矩阵G的秩为MR;G(m)表示中继处第m根天线的放大矩阵,m=1,2,…,MR;Ц3表示多个矩阵沿第3模式排列[12]。根据式(9),式(7) 可表示为[13]
y1=G×1HR1×2(HX)T+N1∈CM1×NP×MR
(10)
y2=G×1HR2×2(HX)T+N2∈CM2×NP×MR
(11)
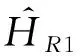
G=I3,MR×1G1×2G2×3G3
(12)
其中,G1、G2、G3∈CMR×MR表示分解的因子矩阵。将式(12)代入式(10)得PARAFAC模型:
y1=IMR×1(HR1G1)×2(XTHTG2)×3G3
(13)
利用式(8),式(13)可写为
[y1](3)=G3[(HR1G1)⊙(XTHTG2)]T
(14)
2 信道估计算法

(15)
为了满足伪逆运算条件,G3设计为正交列满秩矩阵。存在矩阵F1∈CM1×MR和F2∈CNP×MR,使式(15)满足
F1=HR1G1Λ
(16)
F2=XTHTG2Λ-1
(17)
其中:Λ=diag{λ1,λ2,…,λMR}为尺度模糊矩阵;λn是任意复数,n=1,…,MR。在噪声中,式(15) 近似于Khatri-Rao乘积,可根据以下步骤计算F1、F2的估计值:
步骤1 令式(15)左侧等于矩阵Γ∈CM1NP×MR,即Γ≈F1⊙F2。
步骤2 设m=1。
①γm、f1,m、f2,m分别为矩阵Γ、F1、F2的第m列,因此γm≈f1,m⊗f2,m,⊗表示Kronecker积。


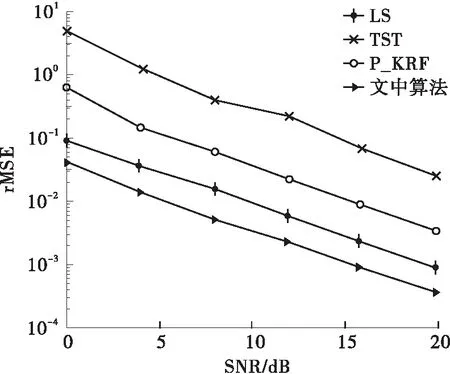
步骤3 如果m (18) 将式(18)代入式(17)得 (19) (20) 式(20)中G2存在伪逆运算,故设计G2为满秩且正交方阵,并将HR1代入式(16)得 (21) 其中:◇表示矩阵元素相乘,Λ=diag{λ}。 在第2节,式(21)求解λ要求M1≥MR;同理,用户2求解λ要求M2≥MR,因此,需考虑min{M1,M2}≥MR和1 情况1 若min{M1,M2}≥MR,由式(21)得 (22) (23) 通过以上步骤求得F1、F2和λ的估计值,最终由式(16)和(17)得到信道矩阵。 (24) (25) 情况2 若1 (26) F1=[f1,1,f1,2,…,f1,MR] (27) (28) 步骤1 如果lj,i已知,利用λλT的对称性,求解未知元素li,j。 步骤2 若还有未知元素,计算比值ρm≜λm/λm-1,m=2,3,…,MR。 ①设m=2; ②获得已知元素lm,i、lm-1,i的列索引i∈I; ③获得已知元素lj,m、lj,m-1的行索引j∈J; ⑤如果m 步骤3 根据比值估计其余部分,对于矩阵L中的未知元素li,j: 考虑到NP≥M1+M2及本节讨论的M1、M2、MR的关系,复杂度因参数设置而定,如表1所示。 表1 算法计算复杂度比较 本节通过MATLAB仿真验证所提方法的性能。以H2R为例,信道估计性能由均方根误差(root Mean Squared Error,rMSE)表征 (29) 其中,p表示信道估计的符号模糊值[16]。rMSE满足高斯分布,其互补累积分布函数(Complementary Cumulative Distribution Function,CCDF)为 (30) 其中,σ2表示方差。 图3分别给出了min{M1,M2}≥MR和1 (a)第一种情况:M1=M2=7,MR=5 (b)第二种情况:M1=M2=3,MR=5 Fig.3 Comparison of rMSE performance of different algorithms 由图3可见,两种情况下,4种算法的rMSE值都随着SNR值的增加逐渐减小,其信道估计能力增强;所提算法的信道估计精度远远优于其它3种算法。由于所提算法可解决非线性最小二乘问题,尤其是当中继的天线数量小于两用户时,信道估计精度更高,与其它3种算法相比,具有一定的优势。 图4给出了M1=4、M2=5、MR=9时,所提算法的误比特率(Bit Error Ratio,BER)性能曲线。 由图4可见,当SNR为10 dB时,两用户发送的符号S1和S2的BER分别约为10-1.8和10-3.4。 图5所示为中继天线数量固定,即MR=6时,min{M1,M2}≥MR和1 M1=M2=MR=4,SNR分别为10、15、20 dB时,所提算法与LS算法关于CCDF的曲线图如图6所示。 图4 所提算法的BER性能 (a)第一种情况:min{M1,M2}≥MR (b)第二种情况:1 Fig.5 rMSE performance of the proposed algorithm under different parameters 由图6可知,相同信噪比下,所提算法的CCDF曲线都比LS算法的更平滑,斜率的绝对值更大,这表明所提算法受噪声影响相对较小,且对信道的估计更稳定。值得注意的是,当所提算法信噪比为10 dB时,其曲线接近LS算法信噪比为20 dB 时的曲线,也表明所提算法的可靠性。 图6 不同算法关于互补累积分布函数的比较 针对双向CCFD AF中继系统,提出了一种基于多维矩阵的信道估计方法,该方法由自干扰消除、多维矩阵建模及信道估计三部分组成,无需在中继处进行信道估计,利用多维矩阵低秩分解及SVD分解特性在用户端估计出所有的CSI。此方法无须迭代,具有较低的计算复杂度,适用于更灵活的天线配置,并且获得了中继放大矩阵和导频序列的设计规则,实现了信道和符号的有效恢复。

3 算法分析













4 仿真结果及分析






5 结语
