双粒度光流流形学习的刮刷总成摆杆摆幅检测

郑思凡 王卫星 何占华 梁子裕 陈平平

(1.福州大学 物理与信息工程学院，福建 福州 350116；2.黎明职业大学 智能制造工程学院，福建 泉州 362000；3.长安大学 信息工程学院，陕西 西安 710064；4.福建慧舟信息科技有限公司，福建 福州 350003；5.黎明职业大学 科技处，福建 泉州 362000)

近年来随着机器视觉、模式识别等技术的不断成熟以及运输组织改变与车辆高速重载新要求的提出，车辆运行故障动态检测系统(Running Trouble of Freight Car Detection System，TFDS)[1]成为交通部大力推广的一套自动安检标准系统，从而为机器视觉在交通运输智能化领域的应用奠定了基础、指明了方向。文献[2]首次提出了基于图像灰度映射、边缘检测、Hough变换等经典视觉算法代替肉眼来实现对机械摆杆故障的识别、定位和分割，但停留在静态的尺寸配合及几何形态方面，未对摆杆的运动特性做进一步定量故障视觉检测研究；另一方面，虽然TFDS[1]在铁路运输方面对解决列车大密度开行与克服人工列检效率低等方面发挥了重要作用，但在公路运输方面，客运汽车安全例检智能信息化水平依然具有较大的发展空间，作为TFDS在公路系统的一个延伸，为了加强地理分布较为分散的客运日趟故障安全例检站的信息化与智能化管理，本研究拟侧重解决客运汽车日趟安检的一个重要内容——在复杂玻璃背景下对车辆刮水器摆杆摆幅的视觉检测，改进基于等长轨迹稀疏子空间聚类的运动分割算法。

从运动目标检测目的考虑，当前较为成熟的算法有基于目标特征提取建模的生成式目标跟踪算法，如增量学习(Incremental Learning for Robust Visual Tracking，IVT)、自适应结构局部稀疏表观(Adaptive Structural Local Sparse Appearance Model，ALSA)、加速近端梯度L1范数跟踪(L1 Tracker Using Accelerated Proximal Gradient Approach，L1APG[3])、视频跟踪分解(Visual Tracking Decomposition，VTD)、采样跟踪器(Tracking by Sampling Trackers，VTS[4- 6])等；以及前景实时在线训练分类器的判别式跟踪算法，如核循环结构跟踪(Circulant Structure of Tracking-by-Detection with Kernels，CSK)、色度空间跟踪(Coloring Visual Tracking CN)、核相关滤波(Kernelized Correlation Filters，KCF)、判别尺度空间跟踪器(Discriminatiive Scale Space Tracker，DSST)、 时空上下文跟踪(Spatio-Temporal Context Learning，STC)、特征融合自适应核相关滤波(A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration，SAMF[7- 9])等。但是上述各算法都是基于块状窗口区域进行特征提取，对于刮水器摆杆这种细长型几何外形并不合适，因此笔者考虑由光流场出发，通过轨迹聚类这种自底向上的方式来检测摆杆运动。当前基于光流轨迹的运动分割有两类：一类是以SFM(Structure From Motion)[10]三维重建理论为基础，将不同运动刚体轨迹聚类到2～4维的低维超平面子空间里，代表性算法有广义主成分分析(Generalized Principal Component Analysis，GPCA)、局部子空间相似度聚类(Local Subspace Affinity，LSA)、低秩分解(Low Rank Representation，LRR)、低秩子空间聚类(Low Rank Subspace Clustering，LRSC)、多段学习(Multi-Stage Learning，MSL[11])、稀疏子空间聚类(Sparse Subspace Clustering，SSC[12])等，其中SSC性能最优；另外一类是以类内类间相似度比最大的流形假定为基础，对稠密变分光流轨迹时空相似度进行谱聚类为架构的运动分割算法(如文献[13- 15])。几何上看，摆杆各自的轨迹呈线性关系分属不同线性子空间，同步运动摆杆的轨迹则共处于仿射子空间，因此可以采用稀疏子空间聚类方法分割不同摆杆，但是SSC等子空间聚类分割算法要求轨迹等长，而雨刮摆动过程中，其边缘会因与玻璃背景中黑色的物体(如顶上雨蓬)融合而造成部分轨迹中断，同时因为光照不同使得摆杆不同部位的轨迹起始点并不完全相同。这样直接采用SSC算法进行分割的轨迹将过于稀疏，导致随机抽样一致性(Random Sample Consensus，RANSAC)拟合的摆杆位置有较大误差，另一方面，稠密光流轨迹谱聚类在构建轨迹时空相似度矩阵时，考虑的是轨迹共有时间段局部速度及位移的相似性，相隔较远的轨迹因相似度低往往聚类为不同类别，导致摆杆两端出现过分割现象。

为此，在综合两类轨迹聚类优缺点后，本研究提出了一种双粒度光流流形学习的汽车刮水器运动分割算法，先将完整的等长摆杆光流轨迹作为粗粒度特征光流轨迹进行稀疏子空间聚类，获得可靠的种子样本；然后通过提高空间采样率得到稠密细粒度大位移(Large Displacement Optical Flow，LDOF[16])变分光流后，再与粗粒度光流构建轨迹时空相似度流形拓扑图，并在图上将种子轨迹样本邻接节点标签离散值分布凸松弛为高斯随机场连续值分布后，利用调和函数进行半监督标签值扩散，从而获得被聚类为同一标签值的稠密的摆杆光流特征点；最后通过对轨迹纵坐标极值所在的帧的光流特征点分别进行逐次RANSAC直线拟合，以获得主摆杆的摆角从而完成雨刮运动的定量检测。

1 LDOF变分光流定义及采集

LDOF是 Ochs等[16]为解决传统KLT光流因局限于结构张量较大的角点导致光流过于稀疏而提出的大位移稠密变分光流，LDOF将求解每一个像素在下一帧图像的最佳位移w=(u，v)值转化为求解如下泛函能量值：

(1)

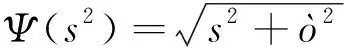
另外，为了正则化光流场，使之分段光滑，定义平滑项如下：

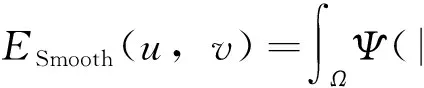
(2)

E(u，v)=EData+αESmooth

(3)

其中：α>0为正则化参数，u与v为待优化的目标位移。为了避免陷入局部最优，上述泛函对应欧拉-拉格朗日方程必须在不同尺度空间求解，即以2为基数下采样3次，先在分辨率最低的尺度空间获取位移解的终值，作为下一层分辨率较高的解初值层层修正细化，最终求得全局最优解。因此对于高速运动雨刮，文中采用浙江大华技术股份有限公司出厂的分辨率为720 p、帧率为60帧/s的DH-IPC-HF5210-I高速枪型相机进行采集，以保证下一帧移动位移在分辨率最低的尺度空间范围内。另外，为了保证实时性，软件上可以采用OpenCV3.4集成的Nvidia GPU加速版的BroxOpticalFlow类完成计算。

为了保证获取足够数量等长轨迹作为后续半监督学习的种子样本，在SSC聚类前应先将低对比度的雨刮背景反色为雾状再通过暗通道去雾滤波环节[17]来增强雨刮作为前景的对比度，效果如图1所示。

(a)去雾前

(b)去雾后

Fig.1 Rendering of enhancing contrast through dehazing in dark channel

2 刮刷总成的机构及摆杆运动独立性分析

由SFM[10]理论可知，在仿射相机模型的条件下，刚体各像素运动轨迹坐标构成的矩阵可以分解为运动矩阵与形状矩阵的乘积。其中运动矩阵由相机的内外校正参数与每一帧刚体相对相机的位姿(旋转与平移)构成；形状矩阵形成刚体外形点云分布，同一刚体的点云轨迹因为共享同一个相机的位姿矩阵而处于同一个线性空间，相机的位姿矩阵在SE(3)连续李群流形里，其秩小于等于4，所以各刚体轨迹均位于不同的4维超平面流形里。但是文献[12]指出，如果不同刚体存在同步运动，则位姿矩阵自由度产生坍缩使得子空间存在部分重叠，因此下面从雨刮的四连杆机构运动机理分析其轨迹独立性。

当前客运车辆较常用的刮水器总成结构由两部分四连杆组成，如图2所示。

图2 刮水器连杆结构

其中L1、L2、L3、L4构成并联摇摆杆机构，L5、L6、L7构成主刮曲柄摆杆系统；并联摇摆杆机构是Grashof连杆的一种特例，起到同步输入动杆与输出杆速度和相位的作用。根据矢量运算原理，文献[18]得到主刮摆杆的角速度如下：

(4)

其中，θ为对应连杆与x轴夹角，ω为相应角速度，同理主刮连杆角速度如下：

(5)

其中，l1，l2，l3的含义同文献[18].

由图2可见，由于驱动杆铆接的位置不同，左右摆杆角速度并不相同，因此左右摆杆运动在这种情况下线性独立，但是在实践中发现，对于小型客车，会存在由严格同步双摇杆驱动的刮水器结构，如图3所示[19]。

图中连杆A、B、C、D构成平行双摇杆，由曲柄EF驱动，因此左右摆杆轨迹位姿旋转分量相同，使得二者在3维仿射空间里存在部分子空间重叠。所以对于同步摆杆的运动分割存在左右摆杆轨迹聚类标识互相交错，出现小型客车雨刮摆杆拟合误差较大现象。

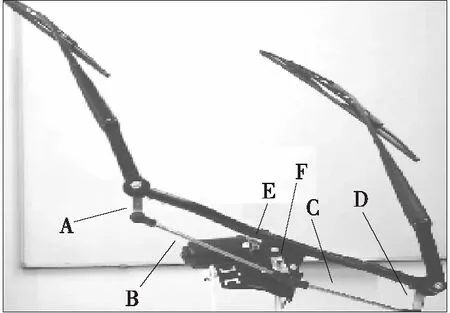
图3 同步双摇杆刮水器结构

3 光流轨迹分布及直接SSC聚类局限性分析

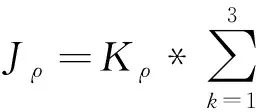
图4 刮水器总的光流轨迹分布

由图4可见，因为背景的复杂性，整体密度与长短分布不均，为得到满幅摆动等长轨迹作为聚类种子，在上述轨迹集合中提取长度大于48帧的轨迹如图5所示。

图5 粗粒度光流轨迹分布

则余下的不等长轨迹可作为细粒度轨迹用于标签扩散，其分布如图6所示。

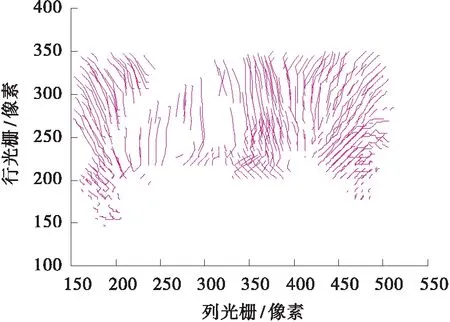
图6 细粒度光流轨迹分布

定义上述粗粒度光流长度48帧为F，则按照文献[12]提出的SSC算法，将上述长度为F的粗粒度光流轨迹每个点坐标按照先横坐标后纵坐标次序排列为矩阵的每一列，每列前F行为横坐标，后F行为纵坐标，各列构成自表达字典并按照下式逐列求其他各列对本列的线性表达系数矩阵C：

(6)

s.t.Y=YC+E，

diag(C)=0，

CT1=1。

其中：C为N×N自表达系数矩阵，N为轨迹数；Y为2Q×N轨迹集合矩阵，Q为帧数；E为误差矩阵；F是Frobenius范数；λ为权衡参数，用以平衡轨迹误差与解的稀疏性及泛函的凸性，在此取0.01。为采用并行运算提高运算速度，文献[12]也提供了此优化函数的ADMM(交替方向乘子法)算法实现，通过引入两个拉格朗日乘子后以并行线程的方式轮流对5个优化变量优化迭代以解得矩阵C。

将矩阵C看为各轨迹所在子空间相似度进行谱聚类，取任一轨迹y坐标极值作为满幅摆动所在帧，可得如图7所示的聚类结果。

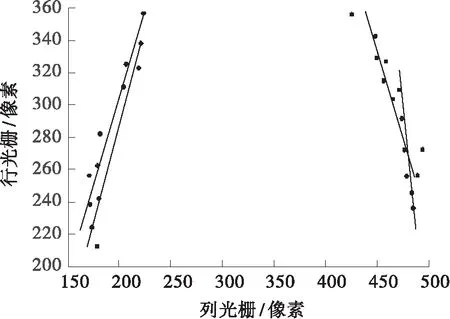
图7 粗粒度光流直接SCC聚类拟合结果

Fig.7 Direct SSC clustering and line fitting results of coarsE- granularity optical flow

由图7可见，SSC准确标识了左右摆杆，但由于过于稀疏，经过RANSAC直线拟合后左右刮刷总成(即主摆杆与副摆杆)均出现较大的角度误差，于是下面将细粒度光流一并考虑，并构建时空相似度图，以借助半监督标签扩散算法完成轨迹进一步稠密的分割提取。

4 双粒度光流流形学习的原理及实现

依前述分析，文中构建两种粒度光流相似度拓扑图，为了充分表达轨迹时空两方面的相似度以区分交叉与相向运动，下面采用文献[20]提出的轨迹位移与速度共有区间的统计值的RBF函数值来衡量轨迹的相似度，轨迹平均偏移距离与速度如下：

(7)

(8)

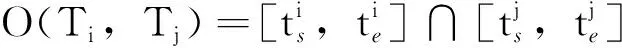
可得两条轨迹总的时空相似度距离为

dvelocity(Ti，Tj)]

(9)

则d(Ti，Tj)的RBF热核映射wi，j即为拓扑图边的权值，按照相似度高的节点标签应尽可能一致的流形聚类假定原则可构造标签扩散目标泛函如下：

(10)

其中：yi、yj为节点i、j标签值。

将上述样本种子标签作为泛函边界条件后，问题可转化为离散状态下马尔科夫随机场对标签的最大后验概率(MAP)的估计问题，如下式所示：

p(y)∝exp(-E(y))|yL=ξ

(11)

为了避免NP问题，文献[21]将标签离散取值凸松弛为种子标签yl=ξ约束的条件连续分布的高斯随机场：

(12)

其中：fU为待求标签平均值；Δ为拉氏矩阵，按照种子与非种子分块定义如下：

(13)

将离散型变量y松弛为连续变量f后将上述带边界条件的二次型泛函(式(10))看为狄利克雷积分离散化形式并对f求其欧拉-拉格朗日方程可得：

Δf=0

(14)

可见f的解即为调和函数，将式(13)分块定义带入式(14)可得待求标签值如下：

fU=-(ΔUU)-1ΔULyL

(15)

为方便矩阵运算，对标签值进行hot-one编码，经过轨迹长度与位移阈值筛选后只剩下左右摆杆两个刚体的轨迹，因热核RBF函数带宽的取值与各轨迹位移与速度的方差有关，考虑到左右摆杆机械上是由同一电机驱动，故在此统一取热核RBF函数带宽σ为1.2，邻接半径ε为20像素，Ncut的K-mean聚类超参数k为2，最后可得标签扩散后的稠密分割结果及相应拟合结果，如图8所示。

由图8可见，摆杆的拟合精度与主摆杆摆角的准确度均得到提高，可以分别得到准确的主摆杆与刮刷总成的拟合直线。

在摆角的计算中，考虑到拟合的直线数目是已知的，因此这里并不需要采用象Hough变换或能量标签值最优的PEARL[22]算法去检测直线数目后拟合，而是通过取较小的拟合误差(10像素)来避免主摆杆与副摆杆被拟合为同一条直线，即采用序列RANSAC的方式对双粒度运动分割得到的点集逐次去除已拟合好的点集，顺次得到左右主摆杆与副摆杆拟合直线。

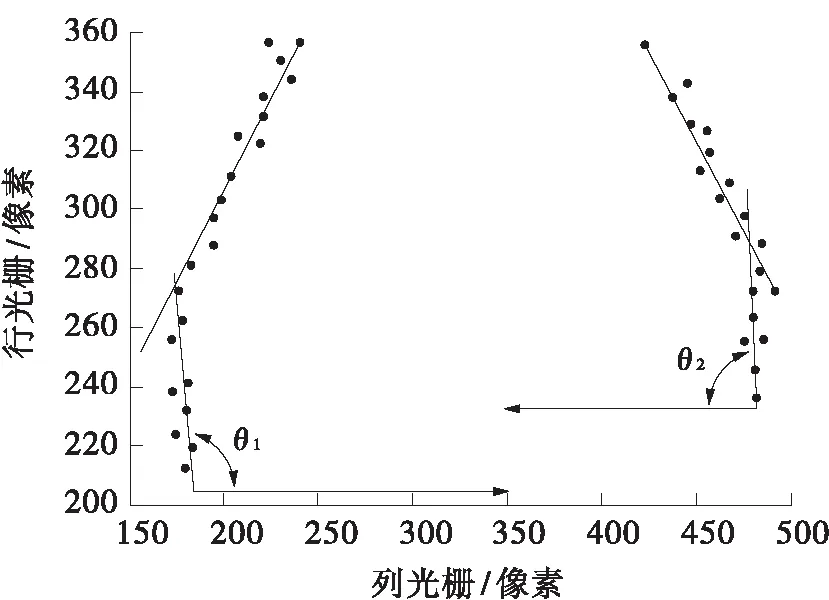
图8 双粒度流形学习后聚类结果

Fig.8 Clustering result after two granularity manifold learning

为了简化计算，根据安检需要，这里只计算摆动过程中摆角极大端处的斜率的反正切值，最小摆角统一默认为0，求得夹角如图8中的θ1与θ2所示，其中θ2为斜率取绝对值后反正切得到，基准线取图中x轴。

综合前述，文中算法步骤如下。

输入：车辆静止后雨刮摆动2 s视频片段、邻接半径ε、RBF带宽σ、聚类数目K、粗粒度光流轨迹长度L、前后光流方向一致性阈值H；

输出：在任何一帧的稠密轨迹标识散点图。

步骤1 以设定的空间采用率求各采样像素结构张量Jρ，取大于张量阈值像素变分光流LDOF[16]，在生成的光流flo文件中对各光流采样点位置进行前后光流方向一致性检查，保留相邻帧大于一致性阈值H的flo光流，小于阈值H的位置重新初始化为新轨迹起点参与下一轮光流采集与方向一致性检查，最终将所有帧的flo文件同一位置小于阈值H的各光流连线形成同一条轨迹保存在轨迹元胞数组元素中；总体上看，不同位置的光流则因遮挡或背景情况不同形成长度不一的轨迹群，这个轨迹群可相应保存在总体的轨迹元胞数组中。

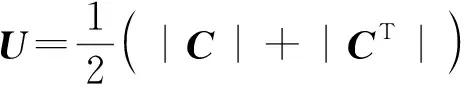
步骤3 将所有轨迹作为节点，按照式(7)-(9)计算各节点在邻接半径ε内边权值wi，j，建立ε-NN近邻矩阵。

步骤4 对标签进行hot-one矢量编码并按照式(15)计算非种子标签的编码值，因为hot-one矢量编码将标签指示的类别值映射到“1”所在的脚标位置，因此可将计算出来的非种子标签的编码矢量最大值分量的脚标位置作为本轨迹的聚类标签值输出。

步骤5 取两类种子轨迹y坐标极值所在帧的散点图逐次进行RANSAC直线拟合和相关摆角计算。

5 算法时间复杂度分析

由上述算法步骤4及式(15)可以看出，双粒度标签扩散在求解时仅仅需要运行1次的逆阵与矩阵乘法运算，并不需要迭代，其时间复杂度远低于单粒度的ADMM算法，为方便定量分析比较单粒度的SSC算法与文中提出的双粒度SSC运动分割算法的时间复杂度，这里假定轨迹数目为n，轨迹均为满幅等长且长度为p(即聚类数据维度)，迭代次数为T，下面通过ADMM的迭代过程分析其时间复杂度。

因式(6)的自表达系数矩阵对角线元素表示元素自身相似度，为方便迭代更新，将对角线元素设置为0并作为辅助矩阵A引入，并以λe与λz分别表示稀疏误差系数与数据重构误差系数，则目标函数可转化为

(16)

s.t.A=C-diag(C)，

AT1=1。

为保证目标函数严格凸性，增加两个惩罚项及惩罚系数ρ，可将原目标函数进一步转化为如下形式：

(17)

s.t.A=C-diag(C)，

AT1=1。

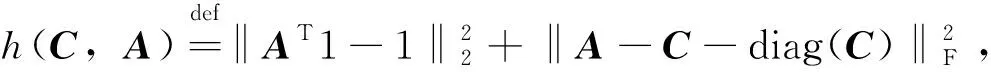
C+diag(C)))

(18)

式中：C，E，A为优化变量；δ，Δ为拉格朗日乘子变量。ADMM算法对这两组变量交替轮流优化如下：

(λzYTY+ρI+ρ11T)A(k+1)=λzYT(Y-E(k))+

ρ(11T+C(k))-1δ(k)T-Δ(k)

(19)

(20)

(21)

δ(k+1)=δ(k)+ρ(A(k+1)T1-1)

(22)

Δ(k+1)=Δ(k)+ρ(A(k+1)-C(k+1))

(23)

可以看出，式(20)-(23)仅包含矩阵加减运算，可以对矩阵元素直接运算，因此ADMM算法的迭代过程主要计算集中在式(19)的矩阵A求逆及YTY的矩阵乘法，二者的时间复杂度为O(n3+n2p)，空间复杂度为n2，考虑迭代次数T，则其总的复杂度为O(Tn3+Tn2p)。

另一方面，假设在n条轨迹中抽取m条轨迹作为种子，并以邻接半径无穷大建立ε-NN近邻矩阵，则双粒度算法最大的时间复杂度为：O(Tm3+Tm2p)+O(n2p)+O((n-m)3+(n-m)2p)。

由上述分析可见，因双粒度算法在降阶SSC后并不需要迭代，在m≪n的情况下可显著降低时间复杂度。不过，m的最小值必须受子空间正确恢复条件限制，即[12]：

(24)

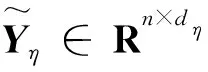
6 客运站测试视频的同步采集与算法测试结果比较

6.1 光流轨迹中断处理及时空域的选取

为了方便批量精确采集雨刮臂的刮动周期所在时间范围、减少运算量，将上述算法模块经过ocx封装后并以回调函数体的形式嵌入客运站的车辆跟踪模块进行同步，当车辆跟踪模块检测到车辆停止在安检地沟停止线附近2 s后以30帧/s的帧率启动光流采集60帧图像作为光流采集总的时间范围。

如前所述，在光流采集中，通过反色去雾提高对比度，通过提高帧率使轨迹连续光滑并保证种子轨迹稠密度，但在实践中，环境照度及玻璃雨篷深色背景等仍然会使采集到的光流轨迹出现中断现象，同一条轨迹经过算法“步骤1”的前后一致性检查后，在黑色背景区域将被隔断为多条较短轨迹，如图9所示。

图9 轨迹中断现象及轨迹时间段选取

Fig.9 Discontinuity phenomenon of trajectory and it’s frame period selection

由图9可见，在60帧满幅摆动中，并不存在满幅长度的轨迹，因此文中提出双粒度分割算法只能在满幅摆动的头尾端提取较短的粗粒度光流来进行SSC聚类获取种子标签，如图9中，算法将粗粒度轨迹长度由正常环境照度情况下的48降为15以获得足够数量的种子，并从中提取y均值最大的轨迹(如图中A、B)覆盖的时间帧作为所有待SSC聚类光流轨迹的采集时间段。

另外，为了避免车灯亮暗变化生成的虚假光流对摆杆光流的影响，系统运行前需要事先采集客运站各车型的车牌、挡风玻璃、各车灯等视觉检测部位的坐标录入数据库，作为每辆车配准前的坐标信息，当有车辆进站准备安检时，车牌识别模块将根据识别出的车牌从数据库调出上述坐标重新配准得到新的坐标，每次配准需要的单应性(Homography)矩阵，则由本车辆事先采集好的车牌及车身logo等面板特征的SIFT描述子与当前进站停止后读取的一帧图像相应面板匹配生成，最后得到实际场景挡风玻璃的坐标范围作为光流的采集空间区域，从而避免车灯亮暗变化的干扰。整体同步采集及坐标配准软件界面如图10所示。

图10 刮动同步采集及坐标配准界面

Fig.10 Software interface for video synchronous acquisition and image registration

6.2 测试结果比较

综合上述，为了区分不同环境照度导致玻璃反光对刮刷摆杆光流结构张量的影响，并同时比较单、双粒度两种算法对于各种光照与车型的总的准确率，本研究在客运站取4种不同车型及6种环境照度共153车次，分别统计拟合误差与摆角误差，其中环境照度由距离挡风玻璃0.5m处利用照度计测量玻璃背景为天空区域的反光亮度值(如图9黄色区域所示)获得，并在不同天气条件下(晴天、阴天、多云、雨天与雾天)以185 lux为间隔均分为6个区段统计测试结果。单粒度算法测量结果取自直接对轨迹长度为15的SSC聚类拟合结果，并将SSC聚类后再进行半监督标签扩散后的拟合结果作为双粒度测量结果进行比较，基准值由人工标定，可得两种算法测量误差如表1所示。

由表1可知，单粒度聚类拟合的误差均值比双粒度高出17.8百分点，这是由于单粒度聚类拟合时因样本点过于稀疏而使主摆杆与副摆杆拟合时存在重叠造成的。

另外，在拟合距离阈值取10像素、迭代次数100的约束情况下两种算法的RANSAC直线拟合误差分布如表2所示。

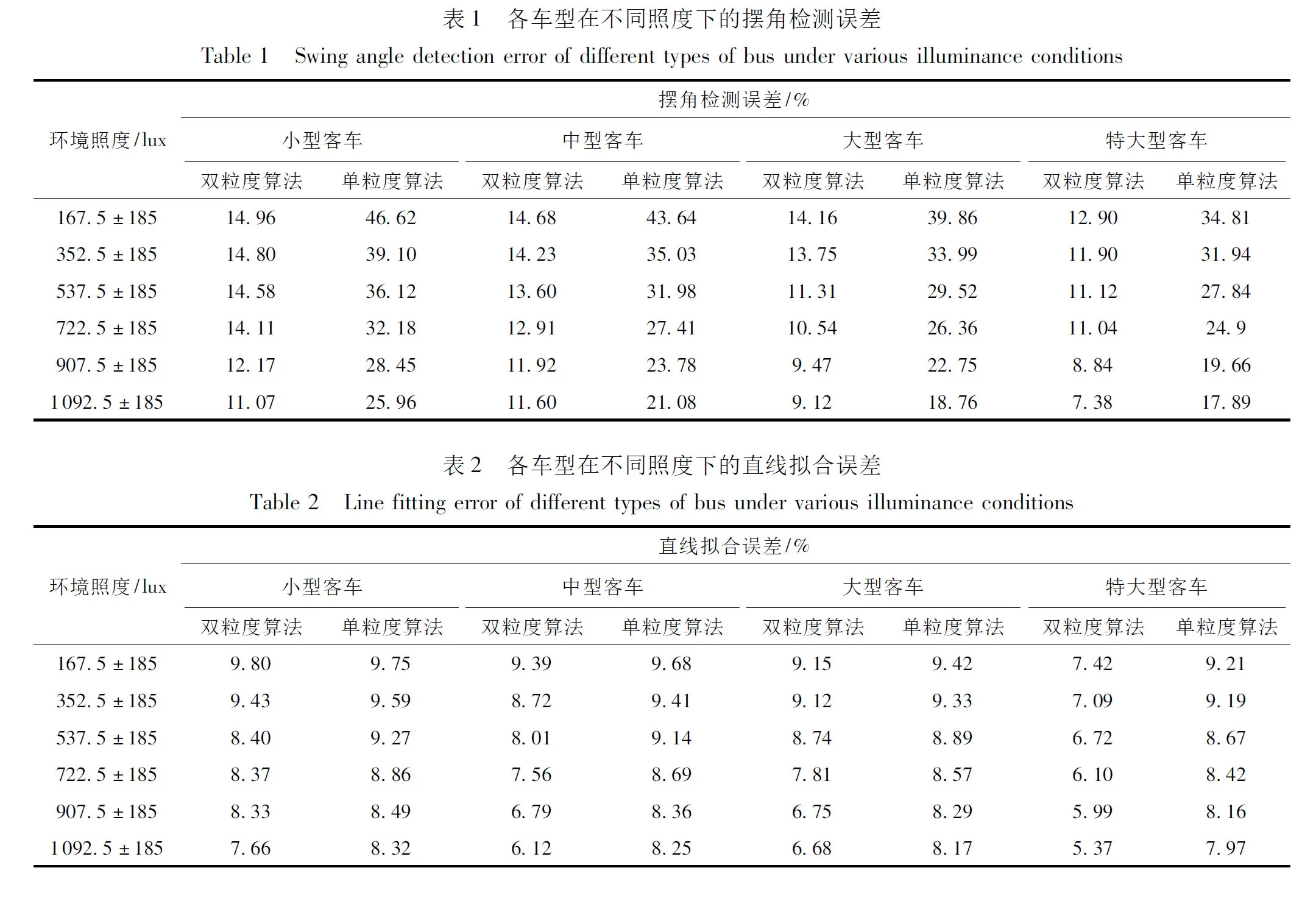
表1 各车型在不同照度下的摆角检测误差

综合表1、表2可见，随着环境照度的提高，拟合与摆角检测精确率均有所提高，这是因为玻璃反光量增加提高了摆杆前景对比度，这样减少了轨迹中断现象使得粗粒度种子轨迹数目增加，同时因前景特征点结构张量增加也增加了总体轨迹的数目与稠密度。总体上看，双粒度算法在拟合和摆角检测二者的误差均不超过15%，工程上可以作为刮水器是否摆动满幅的判断依据。另外，小型客车的拟合误差与摆角误差均高于其他车型，这是前文第2节分析提到的，因为同步雨刮左右摆杆的轨迹处于同一个仿射空间造成的混叠以及采样密度所致。根据式(24)可知在工程上仍然可以通过提高轨迹的稠密度一并解决。

7 结语

针对摆杆细长型单色的机械构件，提出了一种通过光流轨迹聚类的至下而上的运动分割算法。该算法利用的半监督流形学习架构克服了两种粒度轨迹聚类算法的缺点——利用粗粒度SSC聚类种子标签的桥梁作用，很好地克服了细粒度轨迹谱聚类的过分割的缺陷，利用细粒度提供的拓扑信息又可以克服粗粒度的稀疏缺陷。在半监督机器学习成为研究热点的今天，本架构提供了一个很好的研究空间。在实践中本算法并不要求在采集的时间段里光流轨迹都满幅且等长，而仅仅需要这些轨迹存在不同粒度的差别及具有一定长度的种子轨迹即可，因此算法在运动分割中具有广泛的应用范围，同时本算法对摆幅的检测同样适用于对各种仪表盘表针的视觉监控，具有工业应用价值。在软件实现方面，本算法可以封装成ocx插件供其他前端软件模块(如车辆跟踪、车牌识别、经由车牌SIFT匹配的单应矩阵对车灯坐标的配准及亮度变化检测等)以回调函数的形式进行同步并构成一个大的信息化软件系统与客运公司本身的调度系统及运管局的公路电子运政综合执法系统对接，因而也具有在交通运输信息系统的推广价值。