线性连续重复过程的区域极点约束迭代学习控制
2020-02-12汪磊杨慧中陶洪峰WojciechPaszke
汪磊 杨慧中 陶洪峰 Wojciech Paszke
(1.江南大学 教育部轻工过程先进控制重点实验室,江苏 无锡,214122;2.Institute of Control and Computation Engineering,University of Zielona Gora,ul.Szafrana 2,65- 516 Zielona Gora,Poland)
迭代学习控制(Iterative Learning Control,ILC)适用于有限时间重复运行的控制过程,它通过反复学习,利用系统以往的控制经验,不断修正当前的输入信号,实现控制系统对期望轨迹的完全跟踪[1- 3]。迭代学习控制过程能够同时改善系统在时间和周期两个维度上的控制性能,显示出巨大的优越性,因此受到了学术界和工程界的广泛关注[4- 5]。
以往对于迭代学习控制技术的研究大多着眼于被控系统在时域的收敛性[6- 7]。有关频域范围的迭代学习控制研究成果也比较常见,值得注意的是现有的迭代学习控制方法都是在全频范围内讨论系统的稳定性,可保证系统在全频范围内稳定,但这样设计其实具有较大的保守性。因为实际系统往往只需要运行在特定工作频率范围,只需保证系统在有限工作频率范围内的稳定性即可。随着广义KYP引理的应用,迭代学习控制问题深入到有限频域范围。文献[8]将线性重复过程在有限频域的有界输入有界输出性能转化为相应的线性矩阵不等式(Linear Matrix Inequality,LMI)问题,并推广到连续迭代学习控制系统中,但并未同时考虑系统的二维特性;文献[9]基于KYP引理,探讨了线性离散系统在有限频域的鲁棒收敛性;文献[10]则在有限频域范围内设计出前馈-反馈迭代学习控制策略,通过广义KYP引理和LMI进一步分析系统沿时间方向的稳定性及沿迭代方向的收敛性;文献[11]在有限频域中利用KYP引理和LMI分析出了迭代学习控制系统单调收敛及控制器存在的必要条件。然而,上述研究成果关注于迭代学习控制系统在迭代批次方向的鲁棒收敛性,对控制系统在时间方向上的性能关注较少,没有展现出控制系统的动态特征。
鉴于此,本研究将迭代学习控制过程的闭环极点置于指定区域内,基于有限频域研究系统的控制器设计方法,在迭代学习控制作用下,先在时域中将线性重复过程转化为二维(2D)连续Roesser模型;再利用KYP引理,将闭环系统的跟踪性能分析和区域极点约束问题转化为相应的LMI问题,进而获得系统二维特性和动态性能的充分条件;最后,通过实例仿真对文中所提方法的有效性进行了验证。
文中,对于矩阵X,用XT表示其转置,X>0和X<0分别表示矩阵X是正定和负定;I和0分别代表适当维数的单位阵和零矩阵;符号“*”代表对称位置上的元素的转置;sym(A)=A+AT表示方阵A的Hermitian部分;Φ⊗P表示Kronecker乘积;diag{•}表示对角矩阵。
1 问题描述
考虑式(1)所示的线性连续重复过程
(1)
式中:k=0,1,2,…,表示迭代次数;t∈[0,T]为系统的连续时间变量;xk(t)∈Rn、uk(t)∈Rm和yk(t)∈Rp分别是系统的状态、输入和输出;边界条件xk(0)=x0是系统第k次迭代的初始条件;A、B、C和D是相应的适当维数的系统矩阵。
在式(1)所示的系统的迭代学习过程中,令其期望轨迹为yd(t),同时定义跟踪误差:
ek(t)=yd(t)-yk(t)
(2)
其中,期望轨迹满足以下条件:
yd(0)=yk(0)=Cxk(0)。
本研究的目标是设计一种迭代学习控制律,使得系统的实际输出逐渐跟踪上期望轨迹yd(t),同时系统的闭环极点位于复平面的指定区域,保证系统在时间方向上的性能。
对于式(1)所示系统,考虑如下迭代学习控制律:
(3)
式中:uk(t)为本批次的控制输入变量;uk-1(t)为前一批次的控制输入量;Δuk(t)为对控制进行更新的修正量。同时定义
ηk(t)=xk(t)-xk-1(t)
(4)
由式(1)所示系统的初始状态可知ηk(0)=0。利用式(1)-(3)可得:
Aηk(t)+BΔuk(t)
(5)
ek(t)=ek-1(t)-[yk(t)-yk-1(t)]=
ek-1(t)-C[xk(t)-xk-1(t)]-
D[uk(t)-uk-1(t)]=
ek-1(t)-Cηk(t)-DΔuk(t)
(6)
设计迭代学习控制更新律如式(7)所示:
Δuk(t)=K1ηk(t)+K2ek-1(t)
(7)
从而可得如下的2D闭环系统:
(8)
其中:A1=A+BK1,B1=BK2,C1=-C-DK1,D1=I-DK2。
2 稳定性分析

引理1[12]假设W、L和V为给定的适当维数的矩阵,且W和V为正定矩阵,则LTVL-W<0等价于
(9)
或者
(10)
引理2[13]给定适当维数的矩阵X、Y,以及适当维数的对称矩阵Z,则对任意满足ΔTΔ≤I的Δ,不等式
Z+XΔY+YTΔTXT<0
(11)
成立的充要条件是存在ε>0,使得
Z+εXXT+ε-1YTY<0
(12)
引理3[14](投影引理) 设、Λ、Σ为适当维数的实矩阵,且=T,存在矩阵W使不等式

(13)
成立的充要条件为当且仅当以下两个不等式成立
(14)
引理4[15]式(8)所描述的迭代学习控制系统稳定的充要条件为以下条件同时成立:
(i)ρ(D1)<1,其模值严格小于1,保证闭环系统迭代批次方向上的渐近稳定性;
(ii) 矩阵A1的所有特征值均位于复平面的左半平面,保证闭环系统在时间方向上的稳定;
(iii) 传递函数矩阵G(s)=C1(sI-A1)-1·B1+D1,s=jω,∀ω≥0,其模值严格小于1,同时保证闭环系统在时间和批次上的二维性能,使闭环系统稳定。
引理5[16]考虑到系统(式(8))的传递函数G(s)和频率响应矩阵G(jω)=C1(jωI-A1)-1B1+D1,若存在对称矩阵P以及适当维数的正定矩阵Q,满足下式
(15)
那么下列频域不等式也成立
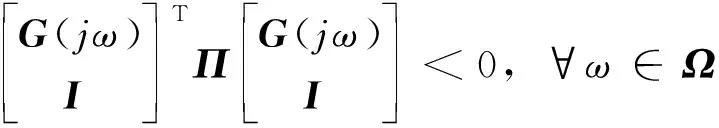
(16)
其中,Π为给定的实对称矩阵,Ω表示频率范围,
Ψ=

此外,引理4的条件(iii)可改写为以下不等式:
|G(jω)|<γ,∀ω∈Ω,γ∈(0,1]
(17)

|Ge(jω)|<ε1,∀ω∈Ω
(18)
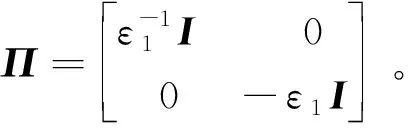
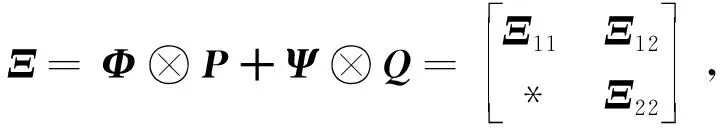
2.1 标称系统的迭代学习控制
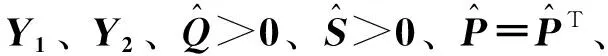
(19)
(20)
其中:
则进一步可得迭代学习控制更新律(式(7))的增益矩阵为
(21)
此时在低、中频段范围内,迭代学习控制律(式(3))作用下的闭环系统(式(8))稳定,同时系统的跟踪误差单调收敛,且系统的闭环极点位于圆心(-q,0)、半径为r的圆域内。
证明若不等式(20)成立,则下列不等式也成立
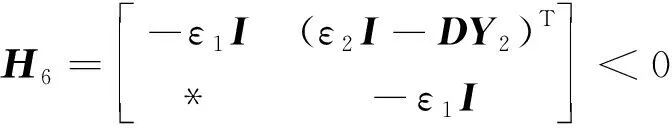
(22)
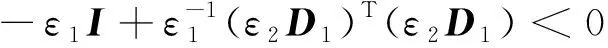
(23)
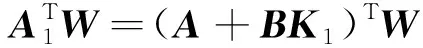
(24)
根据引理3的结论,存在
使得
(Σ⊥)T
(25)
(Λ⊥)T
(26)
由式(25)可得
(Σ⊥)TΣ⊥=
(27)
若不等式(27)成立,当且仅当对角线上元素满足
(28)
由式(20)成立可得,其左侧矩阵对角线上的元素
(29)
由式(26)可得
(Λ⊥)T
(30)
即存在对称矩阵P以及适当维数的矩阵Q>0,满足以下不等式
(31)
根据引理5,式(31)可进一步改写为
(32)
即不等式(18)成立。
另外,根据参考文献[17],若矩阵A1的所有特征值都位于中心(-q,0)、半径r的圆域内,则:
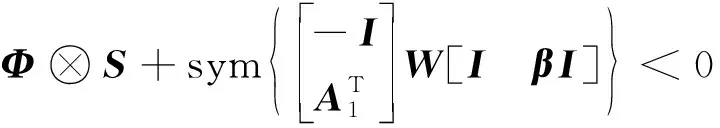
(33)
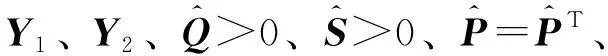
(34)
(35)
其中:
则迭代学习控制更新律(式(7))的增益矩阵为
(36)
此时在高频段范围内,迭代学习控制律(式(3))作用下的闭环系统(式(8))稳定,同时系统的跟踪误差单调收敛,且系统的闭环极点位于圆心(-q,0)、半径为r的圆域内。

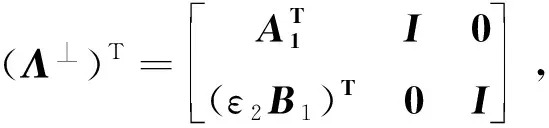
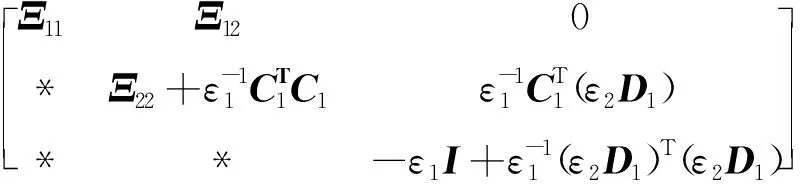
则(Σ⊥)TΣ⊥=
(37)
其余证明过程同定理1。
2.2 不确定性系统的迭代学习控制
在式(8)所示模型的基础上,进一步考虑如下不确定性线性连续重复过程:

(38)
其中,系统的不确定性结构为
(39)
式中:E1、E2、F1和F2是已知的常值矩阵,不确定性扰动系数δ满足
δTδ≤I
(40)
同样采用迭代学习控制器(式(3))及其更新律(式(7)),得到2D闭环模型为

(41)
其中:A2=A+ΔA+(B+ΔB)K1,B2=(B+
ΔB)K2,C2=-(C+ΔC)-(D+ΔD)K1,
D2=I-(D+ΔD)K2。

(42)
(43)
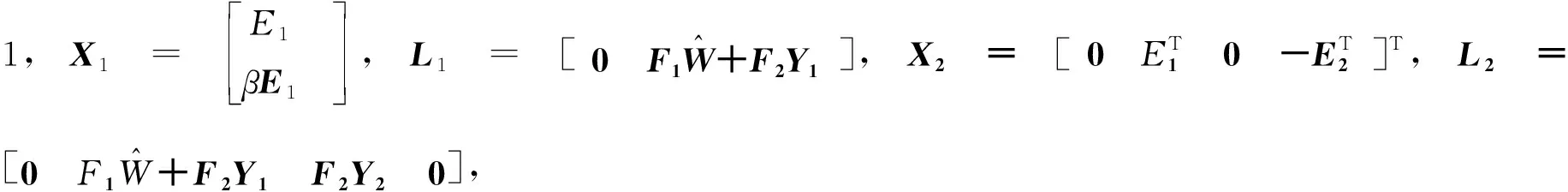
则在低、中频段范围内2D闭环系统(式(41))稳定,同时系统的跟踪误差也单调收敛,并且系统的闭环极点都在圆心(-q,0)、半径r的圆域内,此时迭代学习控制器更新律(式(7))的增益矩阵同样为式(21)形式。
证明根据由定理1的结论,考虑系统的不确定性后,Η12就变为
(44)
由引理2可知,式(44)成立当且仅当存在标量λ1>0,使得以下不等式成立
(45)
运用引理1可得
(46)

(47)
(48)
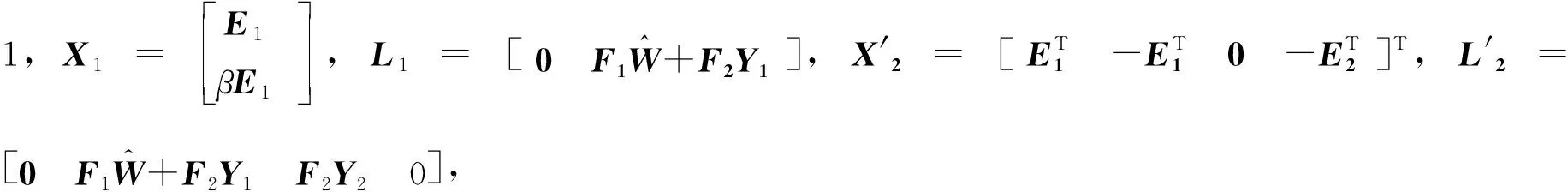
证明在推论1的基础上考虑系统的不确性,证明过程同定理2。
3 仿真结果
为验证文中算法的有效性,考虑典型的跟踪伺服系统,执行机构为单位质量块-弹簧-阻尼器组成的二阶机械位移系统[19],式(1)中状态空间模型参数为

3.1标称系统的仿真

控制系统低频、中频、高频的闭环极点分别是{-3.557 5±j2.982 8}、{-4.343 7±j2.450 7}、{-3.621 1±j2.949 7},都在圆心、半径r=8的圆域内。仿真结果如图1-3所示。由图1-3可见,迭代学习控制系统在各频段都保持稳定。
3.2 不确定性模型的仿真
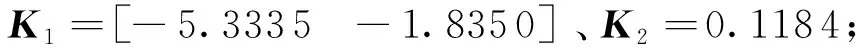

图1 标称系统频域传递函数在低频段的幅值特性曲线
Fig.1 AmplitudE-versus-frequency curve of the frequency domain transfer function of the nominal system over lowfrequency range
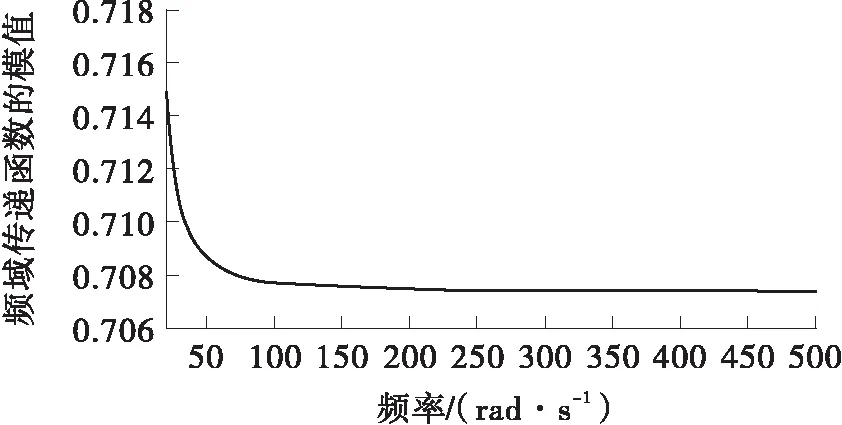
图2 标称系统频域传递函数在中频段的幅值特性
Fig.2 AmplitudE-versus-frequency curve of the frequency domain transfer function of the nominal system over middle frequency range
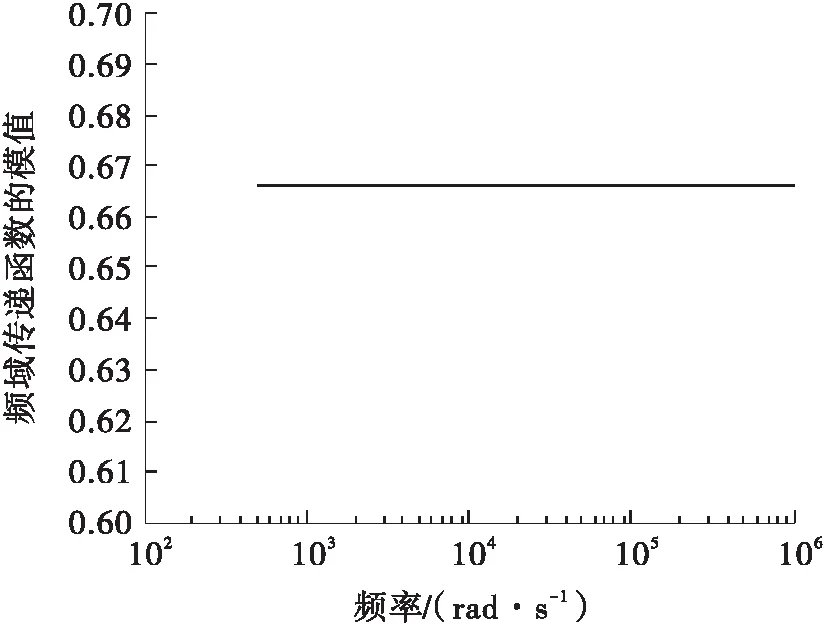
图3 标称系统频域传递函数在高频段的幅值特性曲线
Fig.3 AmplitudE-versus-frequency curve of the frequency domain transfer function of the nominal system over high frequency range
当系统含有不确定性参数时,控制系统的闭环极点分布如图4-6所示,由图4-6可见系统的闭环极点都在指定的圆域内。图7-9为不确定性系统闭环传递函数G(jω)的幅值特性,G(jω)的模值严格小于1,则由引理4可知,不确定性系统闭环系统在时间轴方向上稳定性。
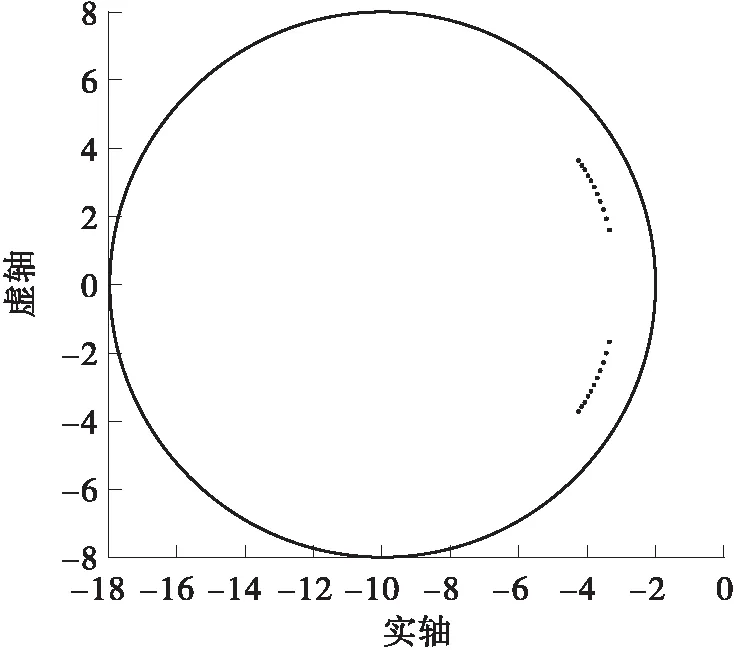
图4 不确定性系统在低频段的闭环极点分布图
Fig.4 Closed-loop pole distribution plot for the uncertain system over low frequency range
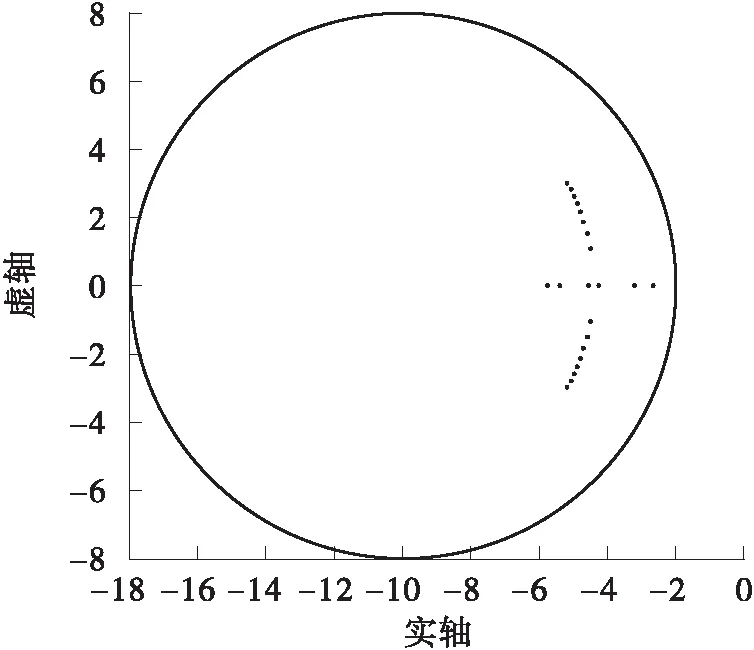
图5 不确定性系统在中频段的闭环极点分布图
Fig.5 Closed-loop pole distribution plot for the uncertain system over middle frequency range
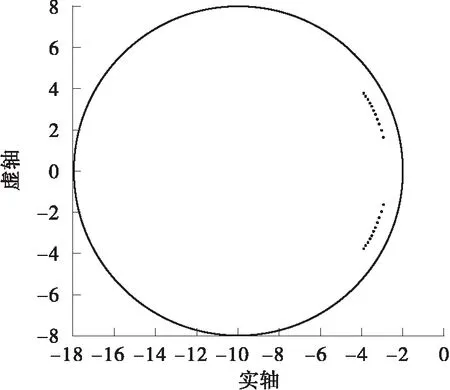
图6 不确定性系统在高频段的闭环极点分布图
Fig.6 Closed-loop pole distribution plot for the uncertain system over high frequency range
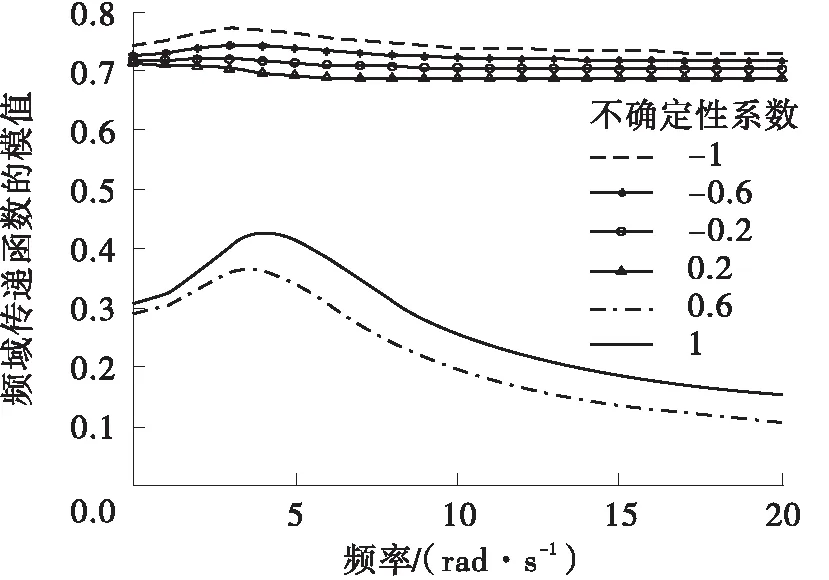
图7 不确定性系统频域传递函数在低频段的幅值特性曲线
Fig.7 AmplitudE-versus-frequency curve of the frequency domain transfer function of the uncertain system over low frequency range

图8 不确定性系统频域传递函数在中频段的幅值特性曲线
Fig.8 AmplitudE-versus-frequency curve of the frequency domain transfer function of the uncertain system over middle frequency range
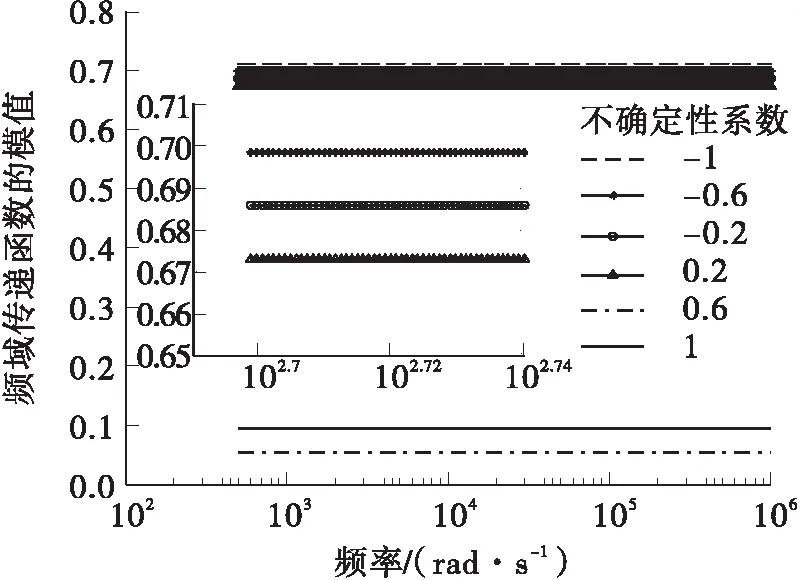
图9 不确定性系统频域传递函数在高频段的幅值特性曲线
Fig.9 AmplitudE-versus-frequency curve of the frequency domain transfer function of the uncertain system over high frequency range
4 结语
文中研究了有限频域范围线性连续重复过程在区域极点约束下的迭代学习控制器设计方案。首先,结合2D系统理论,在时域中建立迭代学习控制系统的2D连续Roesser模型;然后利用KYP引理,将迭代学习控制系统在时间方向和迭代批次方向的性能分析和区域极点约束问题转化为相应的线性矩阵不等式问题,进而给出控制器存在的充分条件及其增益矩阵;最后,通过仿真实验验证了文中所提方法的有效性。
