基于SVD原理的PCA特征频率提取算法及其应用

郭明军 李伟光† 杨期江 赵学智

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.广州航海学院 轮机工程学院，广东 广州 510725)

主成分分析[1](Principal Component Analysis，PCA)是一种基于二阶统计的数据分析方法，通过分析各变量之间的相关关系，利用一组较少的、互不相关的新变量(即主元)来线性表示初始变量。通过PCA方法可以消除随机变量之间的相关性、剔除冗余信息，从而达到突出原始数据中隐含特性的目的[2]。目前，PCA在数字水印[2]、图像处理[3]、模式识别[4]、特征提取[5- 6]及故障诊断[7- 8]等领域都得以广泛应用。Li等[5]将PCA方法应用于工业齿轮箱的状态监测和故障诊断，获得很好的降维和分类效果。Wang等[6]采用PCA提取局部放电故障(PD)信号的多尺度分散熵(MDE)中的有效主成分作为输入特征，然后采用超球面多类支持向量机(HMSVM)进行PD模式识别，实现电气设备绝缘状态诊断。Gharavian等[7]将PCA方法应用于汽车变速器故障诊断。Gao等[8]提出一种融合了EEMD、PCA和PNN 3种方法的改进滚动轴承的故障诊断方法，其中PCA用于故障特征的降维和去除相关性。

确定有效主元的个数是主成分分析的关键问题，常规方法是根据累计贡献率[5- 8]取定某个阈值的方法选择有效主元的个数，其表达式为

(1)

式中，Li表示累计贡献率，λi为协方差矩阵的特征值，δ为某个选定的阈值。由此可见，阈值越大主成分的个数就越多，保留的信息量就越大，从而可能保留的噪声成分也越多。聂振国等[9]提出一种改进的PCA算法，并应用于滚动轴承信号的提纯，取得了较好的效果。李振等[10]研究表明，信号中的每个频率对应两个有效特征值，其幅值决定协方差矩阵的特征值在其分布图中出现的先后顺序，并提出一种基于PCA的算法用于轴心轨迹的提纯。

然而，上述应用当中，都是基于特征值分解协方差矩阵实现PCA算法(姑且称为传统PCA算法)，这种方法计算量较大且存在一定的舍入误差。文献[9]研究结果表明，奇异值分解(Singular value decomposition，SVD)因无需计算协方差矩阵，可以避免舍入误差，且信号的重构误差较传统PCA算法小。鉴于此，文中提出一种全新的思路：基于SVD分解矩阵的原理实现PCA算法。首先，通过理论推导得到协方差矩阵特征值与矩阵奇异值之间的代数关系及协方差矩阵特征向量和矩阵奇异向量之间的对应关系；然后，利用有效特征值与频率分量个数的关系，提出一种基于SVD原理的PCA特征频率提取算法，并通过仿真信号验证算法的有效性；最后，将该算法应用于大型滑动轴承试验台主轴的轴心轨迹提纯中。

1 Hankel矩阵方式下PCA信号处理原理

1.1 PCA信号处理原理

主成分分析[11]是指通过正交变换将一组相关变量xi(i=1，2，…，m)转换为一组线性不相关的变量yj(j=1，2，…，k)，即有：

(2)

式中，系数αi=(αi1，αi2，…，αim)T(i=1，2，…，k)为协方差矩阵C中降序排列的第i个特征值λi对应的特征向量，且αi满足：

(3)

协方差矩阵C的计算式为

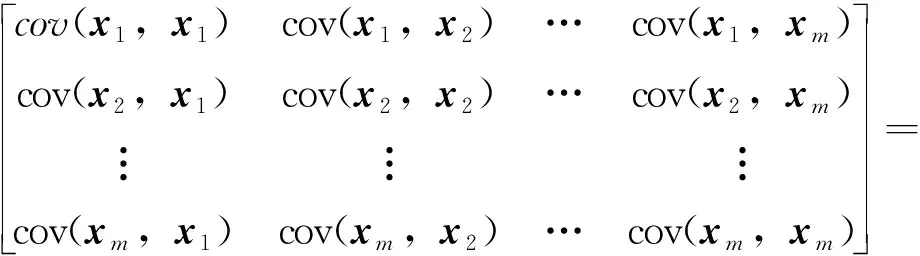
(4)

式中，cov(xi，xj)=E[(xi-E(xi))(xj-E(xj))T]。

协方差矩阵C的特征方程为

Cαi=λiαi

(5)

将式(2)改写为分量形式有：

(6)

其中：yj∈R；j=1，2，…，k。

1.2 Hankel矩阵的构造

在式(4)中，矩阵A采用Hankel矩阵。对于一维零均值的离散信号a=[a(1)a(2) …a(N)]。利用此信号按照以下方法构造Hankel矩阵：

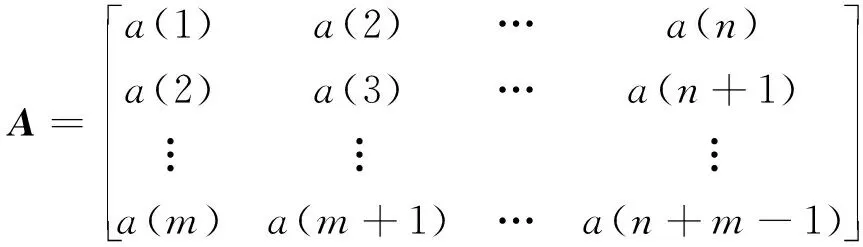
(7)

矩阵A称为重构吸引子轨迹矩阵，也称为Hankel矩阵。针对Hankel矩阵的构造问题，赵学智等[12]证明了噪声去除量与列数呈抛物线的对称关系，并得出结论：如果信号长度N为偶数，应取列数n=N/2、行数m=N/2+1来构造Hankel矩阵；如果N为奇数，应取列数n=(N+1)/2、行数m=(N+1)/2来构造Hankel矩阵。令A=[x1x2…xm]T，其中xi=[ai1ai2…ain]。

1.3 PCA与SVD的关系

由式(5)可见，PCA计算需要用到特征值计算，而且需要计算矩阵A的协方差矩阵。当矩阵A的维数较大时，协方差矩阵的计算量很大，且协方差计算时存在舍入误差[9]。鉴于此，文中提出一种基于SVD的PCA的计算方法，避免了计算协方差矩阵，减少了计算量，同时也避免了协方差矩阵计算时的舍入误差。

对任意实矩阵，其奇异值分解表示为[13]

A=UΣVT

(8)

式中：U=(u1，u2，…，um)∈Rm×m、V=(v1，v2，…，vn)∈Rn×n分别称为左奇异矩阵和右奇异矩阵，且都为正交矩阵，其中ui∈Rm×1、vi∈Rn×1分别称为左奇异向量和右奇异向量；Σ=diag(σ1，σ2，…，σr)为对角矩阵，其元素为按降序排列的奇异值，即σ1≥σ2≥…≥σr≥0(r=min(m，n)是矩阵A的秩)。

构造对称矩阵AAT∈Rm×m，其特征值分解形式为

(9)

根据式(7)可得：

AAT=UΣVT(UΣVT)T=UΣVTVΣTUT

(10)

根据U、V的正交性有：

VTV=E

(11)

式(11)中E为单位矩阵。

又有：

(12)

把式(10)-(12)代入式(9)，得：

(13)

对比式(9)与式(13)可得：

(14)

其中，i=1，2，…，m。

同理可证，对于ATA∈Rn×n存在：

(15)

其中，i=1，2，…，n。

通过上面的推导可知：矩阵AAT或ATA的特征值是矩阵A或AT奇异值的平方，A的左奇异向量是AAT的特征向量，而A的右奇异向量是ATA的特征向量。

1.4 有效特征值数量规律

李振等[10]研究了协方差矩阵的有效特征值(即：非零特征值)与信号参数之间的关系，发现协方差矩阵的有效特征值数量取决于频率个数，而与频率大小及其幅值和相位无关，每一个频率成分总是最多只产生两个非零特征值，频率的幅值越大，则其对应的两个特征值也越大，且这两个特征值总是一前一后紧密排列。据此，根据信号中各频率在幅值谱中的幅值大小排序，就可确定每一个频率对应的两个特征值。

1.5 分量信号重构

根据式(8)和式(14)求出与奇异值对应的降序排列的特征值：λ1≥λ2≥…≥λr≥0。式(6)两边同时左乘αi并求和，可得：

(16)

假设某个特征频率在幅值谱中的幅值大小排序为i，则选择特征值分布图中的第2i-1与第2i个特征值对应的特征向量重构分量信号，将待提取的k个特征频率成分叠加得到近似矩阵Ak：

(17)

(18)

2 基于SVD原理的PCA算法

2.1 算法流程

根据协方差矩阵C的特征值与矩阵A的奇异值及信号频率与有效特征值之间的关系，提出一种基于SVD原理的PCA特征频率提取算法，其具体步骤如下。

步骤1 对一维离散信号a进行零均值处理，去除直流分量，按式(7)构造Hankel矩阵A；

步骤2 对矩阵A进行SVD处理得到降序排列的奇异值σi及左奇异向量ui；

步骤3 根据协方差矩阵C的特征值(向量)与矩阵A的奇异值(向量)之间的关系，由式(14)求得降序排列的特征值λ1≥λ2≥…≥λr≥0及对应的特征向量αi；

步骤4 根据特征值λi分布图及特征频率的幅值排序，选取待提取的k个频率分量对应的特征向量，按式(17)叠加得到近似矩阵Ak；

2.2 信号分析实例

构造一个信号如下：

(19)

从图1(c)、1(d)可知，采用文中的PCA算法提取的单个频率成分与理想信号没有相位偏移，几乎与理想信号完全重合。由此说明，文中提出的PCA算法提取频率的效果很好，且具有零相位特性。

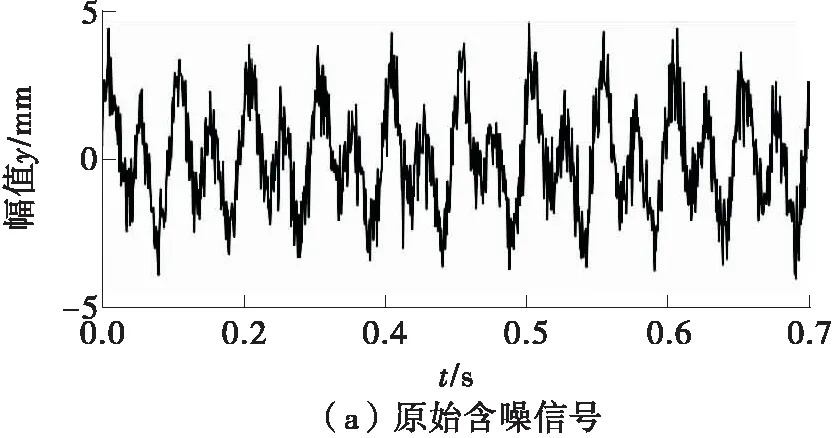
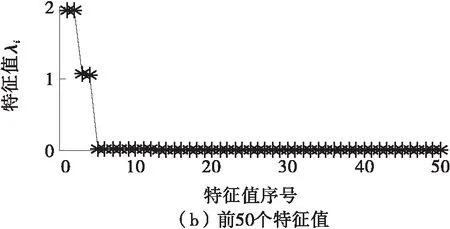
图1 提取含噪信号中的单个频率

3 试验分析

3.1 试验装置

采用课题组自主研发的能够模拟汽轮机实际工况的大型滑动轴承试验台[14]进行滑动轴承的减振性能试验，该试验台主要包括驱动系统、润滑系统、控制系统、采集系统及机械结构等部分;转子两端由试验滑动轴承支撑。为了有效抑制环境干扰采取以下措施：(1)采用空气弹簧有效隔离地基传递到试验台的振动;(2)在小铸铁台面和大铸铁台面之间以及水泥地基与大铸铁台面之间都增加了减振阻尼材料，以降低外界干扰对轴承-转子系统的影响；(3)驱动电机与大铸铁台面之间加丁晴橡胶，削弱电机振动传递的能量。试验台示意图及实物图如图2、图3所示。

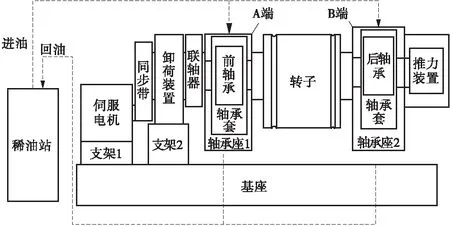
图2 试验台示意图

图3 试验台实物图

3.2 位移传感器测点布置

分别在试验台主轴两端的A、B轴截面两边斜45°位置各布置一个电涡流传感器，所测得的位移信号分别标记为D1、D2、D3、D4，其中A端传感器安装如图4所示。试验所用的便携式LMS SCADASD多功能数据采集系统如图5所示。

图4 位移传感器测点布置(A端)

图5 LMS数据采集系统

3.3 试验方案

正式开展试验前，必须进行预备性试验，目的是确保试验装置能够正常运行，满足后续试验要求。安装好轴承试验件且试验台调试完成后，设定液压站润滑油压力为0.2 MPa、流量为20 L/min，调整转子轴的转速至200 r/min，稳定运行5～10 min，观察监测各参数及数据采集系统。若无异常，则由低转速逐步提升到各工作转速，由LMS数据采集系统采集升速过程中各试验工况下的电涡流位移振动信号。文中仅对主轴A端两个测点位移信号D1和D2进行分析，采样频率为1 024 Hz、采集1 024个数据点。取其中任意3组试验进行分析：(1) 在试验台主轴两端安装轴承试验件1，调试完成后，将转速升至450 r/min (7.5 Hz)；(2) 在试验台主轴两端安装轴承试验件2，调试完成后，将转速升至540 r/min (9 Hz);(3)在试验台主轴两端安装轴承试验件3，调试完成后，将转速升至1 380 r/min (23 Hz)。

试验中得到的信号如图6所示，由图6可知信号的波形难以辨别。各信号的频谱图如图7所示，由图7可知，频谱中包含了随机噪声、转频及其高次谐波等众多频率成分。

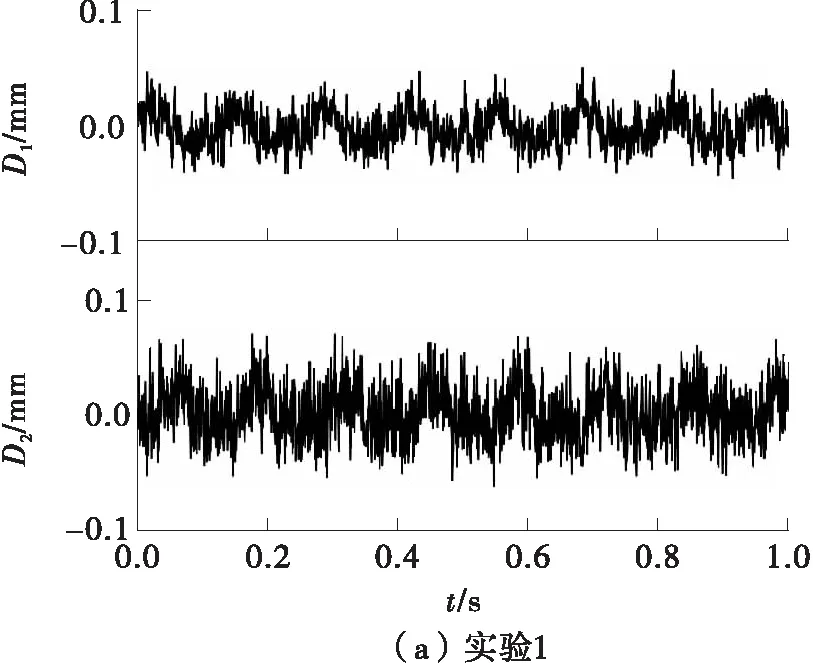
图6 各试验中位移信号的时域波形

图7 各试验中位移信号的频谱图

4 轴心轨迹提纯

根据轴心轨迹的形状可以判断旋转机械的故障类型。研究表明：外“8”字形或香蕉形对应不对中故障，内“8”字形对应油膜涡动故障，规则或不规则的花瓣形对应转子的碰磨故障等[15]。

利用图6和图7的各组试验中两个互相垂直的信号合成的轴心轨迹如图8所示。由图8可知，原始轴心轨迹杂乱无章，这是由于现场测试的振动信号受到了严重的噪声干扰造成的。

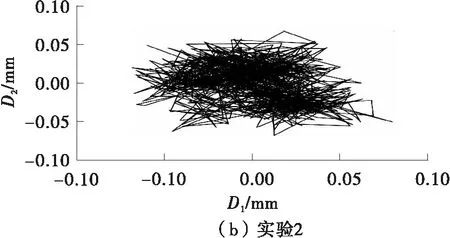
图8 原始轴心轨迹图

对于旋转机械的轴心轨迹提纯，工程中普遍采用的方法是提取转频及其倍频成分中幅值靠前的几个(如 1×、2×、3×等)来合成轴心轨迹，才能得到清晰的图形，进而根据图形进行转子的故障识别。而具体选取哪几个特征频率要结合信号的频谱特征进行分析。

下面采用文中提出的PCA算法对各信号进行分析。首先，利用图6中的各信号按式(7)构造Hankel矩阵Aij(i=1，2，3;j=1，2)，Aij表示第i次试验中的第j个信号所构造的Hankel矩阵；其次，对矩阵Aij进行SVD处理得到降序排列的奇异值及左奇异向量；然后，根据式(14)中的代数关系可求得对应的特征值(如图9所示)及特征向量。由图7(a)、7(b)可知试验1和试验2中的信号1×和2×幅值较大，而其他的频率幅值较小；故对这两组试验中的信号，选取前4个特征值及对应的特征向量，采用平均法[12]重构得到的信号如图10所示，由它们合成的轴心轨迹如图11所示。

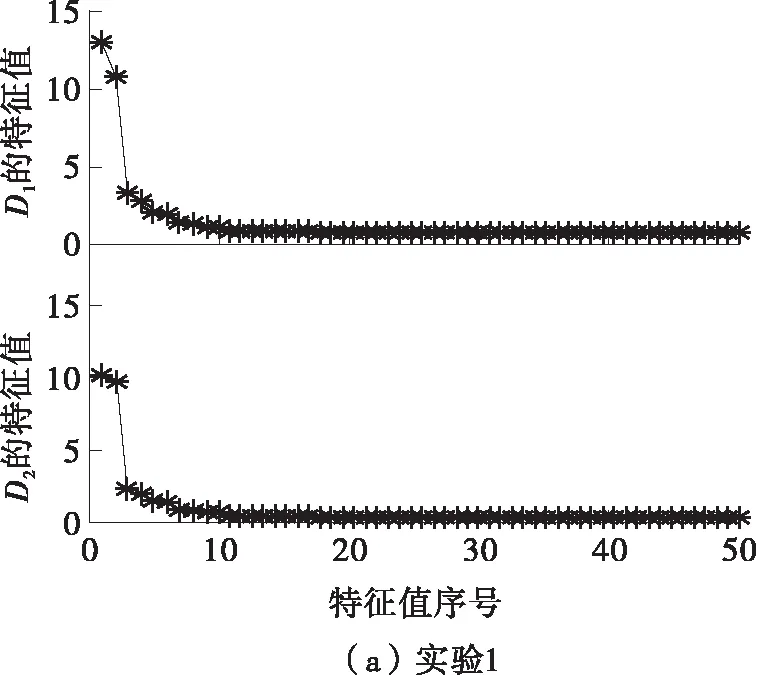
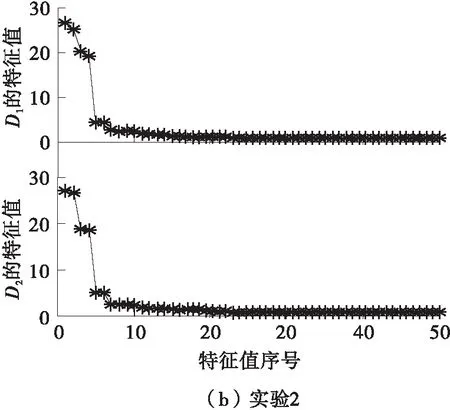
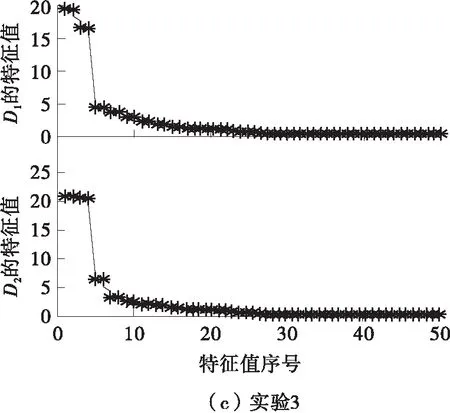
图9 特征值分布图

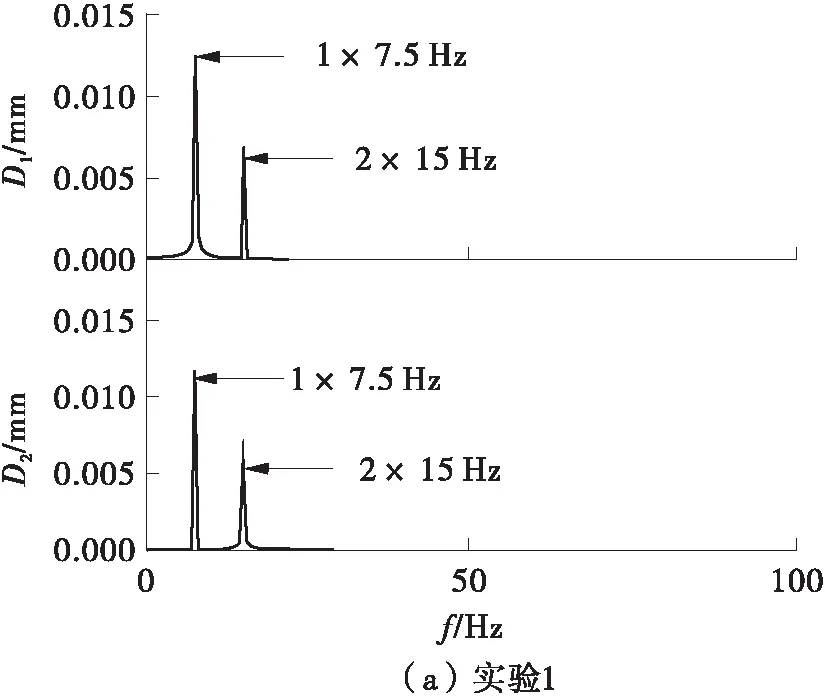
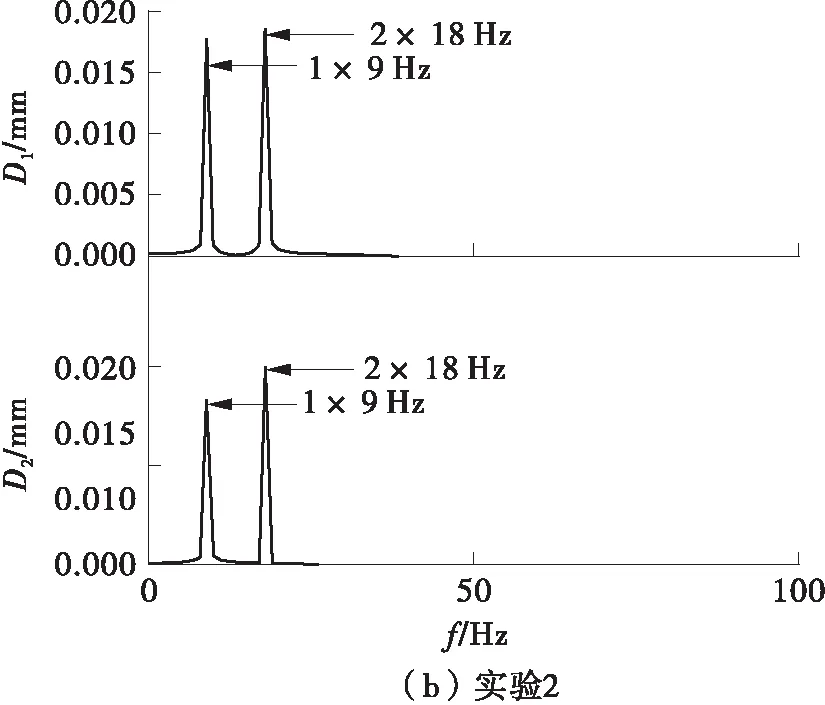
图10 从试验1和2中提取的特征信号

图11 试验1和2中提纯的轴心轨迹

图11(a)中的轴心轨迹为椭圆形，由图11(a)可知，轴心轨迹为椭圆形(长短轴尺寸相近)，说明转子存在轻微不平衡故障，这是因转子的加工工艺、制造误差等因素造成且无法避免的，通常视为正常状态。而11(b)中的轴心轨迹为“香蕉”形，说明转子存在不对中故障。由图10中的特征信号可以发现，正常信号(图10(a))的特点是1×信号的幅值比2×的大得多，而不对中信号(图10(b))中的2×幅值大于1×。

接下来分析试验3的振动情况。由图7(c)可知，试验中信号的1×和3×幅值较大，而其他的频率成分幅值较小。故对试验3中的信号，选取前4个特征值及对应的特征向量，采用平均法[12]重构得到的信号如图12所示。由图12中的信号合成的轴心轨迹如图13所示，由图13可知，提纯的轴心轨迹为花瓣形，说明转子存在碰磨故障。

图12 从试验3中提取的特征信号

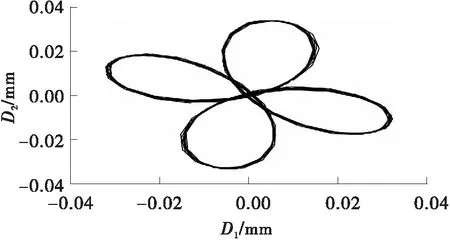
图13 试验3中提纯的轴心轨迹

5 结语

本研究首先从理论上推导了矩阵奇异值(奇异向量)与协方差矩阵特征值(特征向量)之间的对应关系，经推导得出，协方差矩阵的特征值在数值上等于矩阵的奇异值的平方，左奇异向量对应特征向量；然后，研究了Hankel矩阵方式下，主成分分析方法处理信号的分解及重构原理，根据上述结论及有效特征值与频率参数之间的关系，提出一种基于SVD原理的PCA特征频率提取算法，并通过仿真信号验证了算法的有效性；最后，将本研究提出的PCA算法应用于大型滑动轴承试验台主轴的轴心轨迹提纯，得到清晰的轴心轨迹，成功识别了转子的不对中故障和碰磨故障。该算法同样适用于其他旋转机械，具有广泛的应用前景。