一种模型决策森林算法*
2020-01-11门昌骞王文剑
尹 儒,门昌骞,王文剑
1.山西大学 计算机与信息技术学院,太原030006
2.山西大学 计算智能与中文信息处理教育部重点实验室,太原030006
1 引言
近年来,集成学习因其良好的泛化能力在很多现实领域得到了广泛的应用:智能交通中的行人与车辆检测;视频或者图像中出现的物体识别、动作检测;生物信息学研究中的癌症预测、基因组功能预测;数据挖掘领域中的数据流挖掘等。随机森林是集成学习的代表算法之一,它将多棵决策树的结果进行集成并以投票或者其他的方式将最后结果输出,具有简单高效等优点。
在集成学习的研究中,国内外学者先后提出了很多行之有效算法。这些算法主要有两种思路:一种是基学习器之间存在互相依赖关系的Boosting 方法;另一种是基学习器相互独立,没有任何依赖关系的Bagging 方法。
1979 年Dasarathy 和Sheela 首次提 出了集成学 习的思想[1],随后有学者证明弱分类器集成后形成的分类器比其中任一基分类器的分类效果都好[2-3]。1997年,Freund 和Schapire 在Boosting 思想的基础上提出了Adaboost(adaptive Boosting)算法[4]。该算法能够有效提升学习器的精度,并且它将集成的思想扩张到多分类问题和回归问题中。但Adaboost 算法也存在一定缺陷,比如对噪声比较敏感等[5-6]。2001 年,Friedman 提出基于残差的GBDT(gradient Boosting decision tree)算法[7-8]。GBDT 算法具有预测精度高、适合低维数据等优点,但当数据维数高或者数据量大的时候,算法时间复杂度会不断变高。针对GBDT 的缺点,Chen 等人于2016 年提出了XGBoost(extreme gradient Boosting)算法[9]。该算法高效实现了梯度提升,加快了模型训练速度,提高了算法的预测精度。之后,微软在2017 年的NIPS(neural information processing systems)大会上提出了比XGBoost 更快的LightGBM[10]算法。
1996 年,Breiman 提出了Bagging(bootstrap aggregation)算法[11]。Bagging 算法能够通过降低基学习器的方差来改善泛化误差,在大规模数据集上的分类性能较好。这些优点使得Bagging 算法在生物信息学[12]和遥感领域[13]得到了广泛的应用。2001 年,Breiman 提出了随机森林(random forest,RF)算法[14],它将Bagging 的理论与随机子空间方法[15]相结合。随机森林将决策树作为基学习器,利用重采样技术从训练集中生成不同的样本子集,从而训练出不同的决策树,最后使用投票策略进行预测。2006 年,Rodriguez 等人提出了一种旋转森林算法(rotation forests)[16],该方法用PCA(principal component analysis)将样本属性进行映射后生成随机森林。2008 年,Liu等人提出了一种适用于连续数据异常检测的iForest(isolation forest)[17],这种方法具有较低的时间复杂度和较高的准确度。2013 年,Ye 等人提出了一种层次随机森林(stratified random forest)[18],该方法利用Fisher 判别将样本属性分为两部分来生成随机森林。2016 年,Wang 等人提出了伯努利随机森林(Bernoulli random forests)[19],该方法是用两个伯努利分布来选择最优特征与其对应的最优分裂值。2017年,Zhou等人提出了一种深度随机森林(gcForest)[20],这种方法采取了级联森林和多粒度扫描策略来生成随机森林。
模型决策树(model decision tree,MDT)[21]是一种加速的决策树算法。它并没有像传统决策树一样将递归程序执行完,因此其训练速度会比传统决策树快,当然分类错误率与传统决策树相比也不会太差,并且在有的数据集上误差比传统决策树更小,但是随着非纯伪叶结点规模的增大,模型决策树的精度也在下降。本文针对MDT 存在的缺点,利用随机森林的优点,提出了一种模型决策森林(model decision forest,MDF)算法。
2 模型决策森林
2.1 MDT 简介
模型决策树是一种加速的决策树算法,它能够在算法精度不损失或者损失很小的情况下,提高决策树的训练效率,并且具备一定的抗过拟合能力。
MDT 的构建过程为:首先根据当前需要分裂的结点上训练数据的最优特征来进行划分,然后在决策树增长到一定程度时停止,此时得到的是一棵不完全决策树,其最深层上的结点或者是叶结点,或者是非叶结点,但包含的样本属于同一类别(称之为纯伪叶结点),或者是非纯伪叶结点。最后在不完全决策树的非纯伪叶结点上增加一个简单分类模型,生成模型决策树。
2.2 MDF 基本原理
模型决策森林将模型决策树作为基分类器,因此MDF 算法的第一阶段是生成多棵不同的模型决策树(即构建MDT)。在多棵树的生成过程中,通过旋转矩阵来产生不同的样本子集进而生成不同的模型决策树。设给定的训练集为D={(x1,y1),(x2,y2),…,(xn,yn)},其中,xi∈Xn×N,yi∈Yn×1,n为训练集的样本个数,N为特征个数,特征集设为F,基分类器的个数为L。旋转矩阵的计算方式如下:
(1)将特征集F随机分割成S份,则每份包含的特征个数为M=N/S。
(2)令Fi,j表示训练第i个分类器所用到的第j个特征子集。从训练集Xi,j的所有样本中随机抽取一定比例的样本生成,在Fi,j中的M个特征上运行PCA 算法,并把得到的主成分系数保存下来。这里只在上进行PCA 转换是为了尽量避免在不同的基分类器上可能选择相似的特征子集而产生相似系数的情况。
(3)最后将得到的所有系数进行组合,得到矩阵Ri,如式(1)所示。
(4)将Ri根据F中的特征顺序重新排序,得到最终的旋转矩阵。
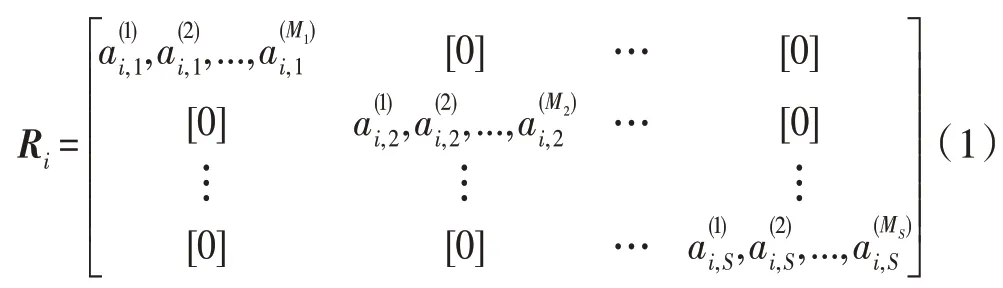
假设训练数据有K个类,Ck指D中属于第k类的样本子集。则给定的训练数据D对应的基尼指数为:
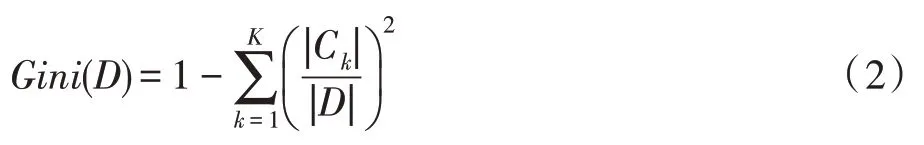
对于二分类问题(K=2),训练数据集D根据某一特征A是否取某一可能值a被分割为D1和D2两部分,即:

因此在特征A的条件下,集合D的基尼指数为:
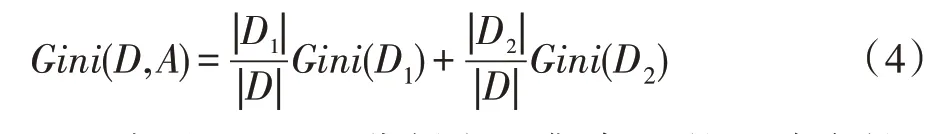
Gini(D,A)表示经A=a分割之后集合D的不确定性,值越小表示训练集的不确定性越小,相反越大则代表训练集的不确定性越大。
根据式(4)分别计算出每个特征的所有可能取值对训练集的基尼指数,然后对比它们的大小,选出其中最小值作为最优特征和最优切分点。
MDF 算法的第二阶段是生成集成模型,本文采用简单平均法将每棵模型决策树的分类结果结合,具体公式如下:

2.3 MDF 算法
本文提出的模型决策森林算法是通过旋转矩阵得到不同的样本子集,从而训练出不同的模型决策树,再将不同的模型决策树集成得到最终的分类器。具体步骤如下:
算法1MDF 算法
初始化:训练数据集D,测试数据集T,树的棵数为L,特征集F,随机分割份数S。
步骤1将F分割为S份,则每份包含的特征个数为M=N/S。从训练集Xi,j的所有样本中随机抽取一定比例的样本生成,在Fi,j中的M个特征上运行PCA 算法,并把得到的主成分系数保存下来。将得到的所有系数按照式(1)组合,并重新排序,得到旋转矩阵。
步骤2计算,得到不同的训练样本子集。在样本子集上根据式(4)计算基尼指数,选择最佳分裂点,直到非纯伪叶结点的规模小于给点参数时停止建树,然后在非纯伪叶结点上用一个简单分类模型构建成模型决策树。
步骤3重复步骤1 和步骤2,直到模型决策树的棵数达到L。
步骤4将得到的L棵树根据式(5)集成起来得到模型决策森林。
步骤5算法结束。
3 实验结果分析
3.1 实验环境及实验数据
本实验使用10 个典型的UCI 二分类数据集进行测试,如表1 所示。实验结果为每个数据集运行多次求出的均值,以尽量避免实验结果的偶然性。实验中采用的计算机硬件配置为:CPU Core i7-3 770,3.40 GHz,内存8.0 GB。

Table 1 Datasets used in experiments表1 实验数据集
实验中基分类器模型决策树的参数设置为高斯核,t设置为0.1。为了方便实验,在模型决策森林的计算中没有固定特征集F随机分割的份数S,反而固定了每份包含的特征个数为M,根据公式S=N/M,即可求得S的大小。这两者任意给出其中之一可求得另一值,且无论先给出哪一值对实验结果都不影响,故本文为便于实验先给出M。实验中可能会遇到数据集的特征数无法被M整除的情况,本文选择将整除M后的余数个特征作为最后一个特征子集。例如:训练集8 维,M=3,那么按照本文方法所有特征分为3 个特征子集,包括两个含有3 个特征的子集和一个含有2 个特征的子集。
3.2 实验结果与分析
(1)参数L对实验结果的影响
在随机森林中树的数量的变化会影响随机森林的精度。当树较少时,RF 的分类错误率比较高,算法性能比较差;当树较多时,RF 的分类精度会随之提升,但是这也意味着RF 的复杂度变高,构建时间变长,森林的可解释性也慢慢减弱。因此为了了解树的数量对MDF 的影响,本文考察L从小变大的情况下算法的分类错误率的变化,具体结果如表2 所示。
表2 中最后一列给出了10 个数据集在不同L下错误率的平均值。从表2 的实验结果总体来看,在这10 个数据集上MDF 算法的分类错误率随着L的增加变化幅度不大。在有些数据集上MDF 算法的分类错误率会随着L的增加而先减小后增大,有些数据集上会先增大后减小,剩下的数据集则随着L的增大变化不明显。虽然表中的分类错误率随着L的变化情况不一致,且错误率的最小值分布在不同的L下,但是错误率的最小值与表中其他错误率值的差距也较小。
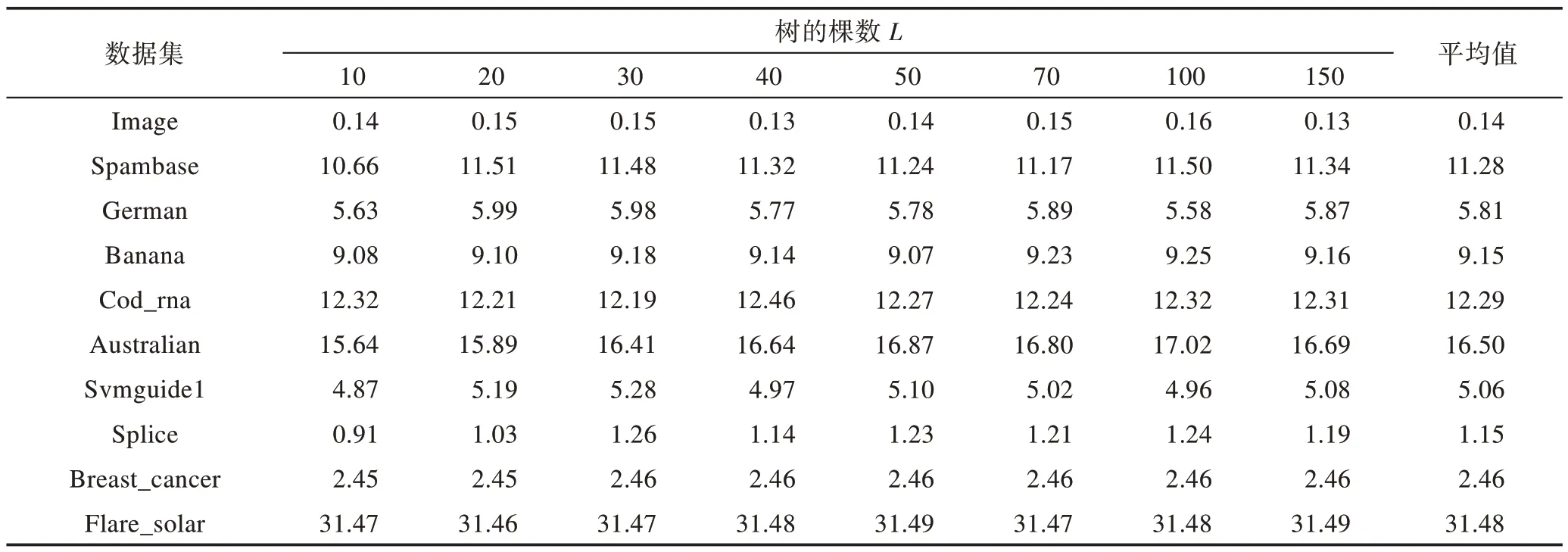
Table 2 Effect of parameter L change on classification error rate表2 参数L 变化对算法分类错误率的影响 %
为了更好地说明不同L下的MDF 算法错误率的变化情况,选取了每行数据的3 个特征值来考察,具体如图1 所示。

Fig.1 Error rate of MDF algorithm under 3 indices图1 在3 种指标下MDF 算法的错误率
图1 中柱状图分别表示每个数据集在L从10 变化到150 时错误率的最小值、平均值和最大值。从图中可以看出每个数据集的3 种柱的高低都比较接近,这也说明最小值与最大值、最小值与平均值以及最大值与平均值之间的差值较小。
综上所述,MDF 的分类错误率随L的变化幅度较小,可以得出模型决策森林的分类错误率对L的变化不敏感。因此本文后续实验取L的值为10,这样既可以获得与较多树时相近的分类错误率,也会避免因树的数量增多而引起的MDF 复杂度变高,训练时间变长的问题。
(2)参数M对实验结果的影响
实验中M的大小不同会产生不同旋转矩阵,即会产生不同的训练样本子集,进而影响模型决策森林的精度与训练时间。如果M太小可能选不到最佳分裂特征与其对应的最佳分裂结点,从而影响MDF算法的分类精度;如果M太大可能会使MDF 算法的训练时间变长,从而影响算法的时间效率。因此合适的M对本文所提MDF算法至关重要,故本文考察了不同的M下算法分类精度的情况,实验结果如表3所示。
表3 中分别列出了M取2~20 的情况下10 个数据集的分类错误率,表中横线表示数据集的特征数没有当前M大的情况。比如:Breast_cancer 数据集9维,它的M最大可取到9,此时只有一个特征子集。因此在表中M取15 和20 的情况下,Breast_cancer 数据集在对应位置标为横线。
根据表3 可以看出,当M为2 时,大部分数据集上的分类错误率都比M为3 时大;而当M大于3 时,在有的数据集上,分类错误率在下降,有的数据集上分类错误率则有一些波动。很容易想到:随着M的不断增大,单棵树在构建过程中选择分裂结点时可以有更多的特征加入到计算中,那么选中最优分裂特征的概率也在不断增大,因此M增大MDF 算法的分类错误率应该逐渐下降。但是在有些数据集上随着M的增大,分类错误率却也在增大,猜想是因为随着特征的增多,可能会在一定程度上造成一些过拟合的现象,尤其是对于特征数较少或者样本数较少的数据集。对于特征比较多的数据集,即使M的取值较小,在构建单棵树的过程中可能会选不到较好的结点,但是本文的单树是模型决策树,在非纯伪叶结点上还存在一个简单分类器,因此最终的分类结果不会太差。

Table 3 Effect of parameter M change on classification error rate表3 参数M 变化对算法分类错误率的影响 %
综上所述,在M=3 时算法的分类错误率具有一定的优势,并且M的值较小时有利于减少MDF 算法的训练时间,故本文在后续实验中将M的值设定为3。
(3)与模型决策树算法的比较
本文方法的基分类器是模型决策树,故将MDF与MDT的分类错误率进行了比较。其中MDF的M取值为3,L取值为10;MDT 中SVM 高斯核参数γ取值为0.5,线性核与高斯核的C都取1.0,LIBLINEAR模型参数s取2,模型叶结点参数t取0.1。实验结果如表4,其中涉及到的模型决策树算法具体含义如表5所示。
表4 中加粗数字表示每行的最小值,最右边一列best other 表示除了MDF 算法外的另外6 种方法在每个数据集上错误率的最小值。从表中可以看出,MDF算法在7 个数据集上分类错误率最小,MDTFS_LIB算法在两个数据集上错误率最小,MDT_SVM(linear)算法在1 个数据集上错误率最小。根据表中best other 这一列可以看出,在几个数据集上虽然本文提出的MDF 方法分类错误率不是最小,但是本文的错误率与其他方法的最小分类错误率相比也较接近,只有在Cod_rna 数据集上本文方法与其他方法最小值相差较多。为了更直观地展现几种方法的实验结果,将表4 中的错误率转化为正确率(100%-错误率)进行比较,如图2 所示。
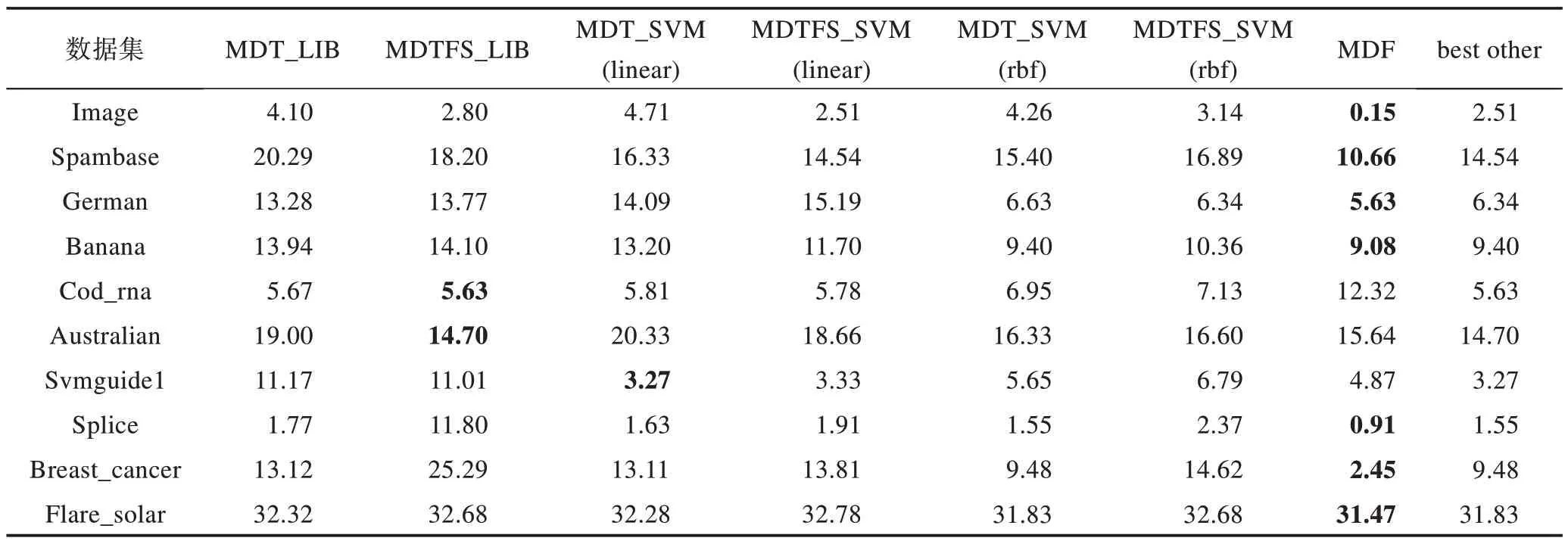
Table 4 Classification error rate of 7 methods表4 7 种方法分类错误率 %
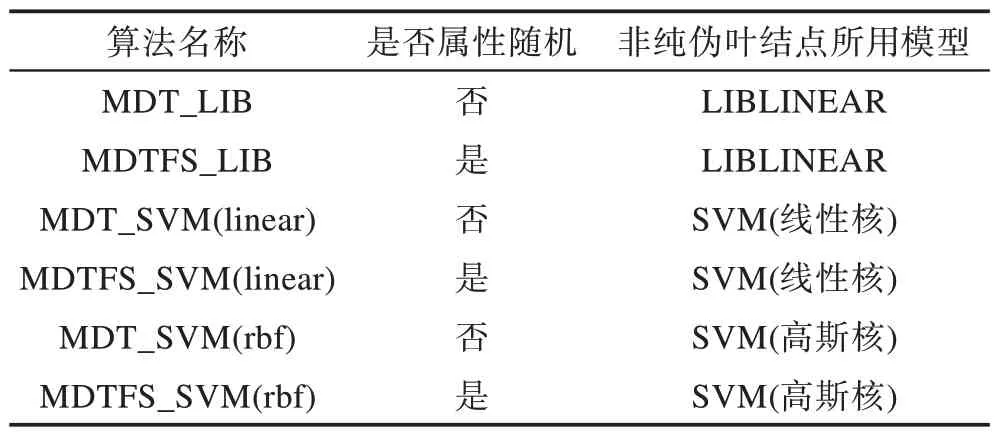
Table 5 Algorithm list表5 算法一览表
图2 的每个子图中,纵坐标都表示本文提出的MDF 算法的正确率,横坐标分别表示其他6 种方法的正确率,图中对角虚线表示横纵坐标对应的两种方法正确率相等的情况。图中一个黑点代表一个数据集,每幅子图都有10 个黑点,代表10 个数据集。黑点在虚线的上方则表示在当前这个数据集上MDF算法的正确率高于横坐标对应的算法的正确率,同时黑点离虚线的垂直距离越大则表示MDF 算法正确率比横坐标对应算法正确率高得越多;黑点在虚线的下方则表示在当前这个数据集上横坐标对应的算法的正确率高于MDF 算法的正确率,同时黑点离虚线的垂直距离越大则表示横坐标对应的算法的正确率比MDF 算法正确率高得越多。
根据图2 可以看出,在这6 幅子图中虚线上方的黑点数量均多于虚线下方的黑点,这表示MDF 算法在多数数据集上的正确率高于其他6 种算法的正确率。在第一行前两幅子图中,MDF 算法的正确率分别在9 个数据集和8 个数据集上比MDT_LIB 算法和MDTFS_LIB 算法高,并且这些数据集中有6 个数据集上的正确率比这两种算法正确率高得较多。在第一行第三幅图和第二行第一幅图上,MDF 算法的正确率各在8 个数据集上比MDT_SVM(linear)算法和MDTFS_SVM(linear)算法高,并且这几个数据集中有3 个数据集离虚线的距离较近,这也表示它们的正确率比较接近。在第二行的最后两幅子图中,MDF 算法的正确率各在9 个数据集上比MDT_SVM(rbf)算法和MDTFS_SVM(rbf)算法高,并且倒数第二幅子图上横纵坐标代表的算法的正确率更加接近,最后一幅子图中MDF 算法的正确率比MDTFS_SVM(rbf)算法更高。
表6 给出了上述7 种方法分类性能优劣的排序结果。表6 中,每一行的值表示该列对应算法比其他列对应算法在该行对应数据集上错误率小的算法个数,这个值最大可为6,最小可为0。例如:第3 行第5列的数字4 表示在German 数据集上MDT_SVM(rbf)算法比其他4 种算法的错误率小。表6 中最后一行是每种算法在各个数据集上的错误率比其他算法小的个数总和。从表6 中可以看出,表现最好的是MDF算法,其次是MDT_SVM(rbf)算法,排在第三位的是MDTFS_SVM(linear)算法,排在最后一位的是MDT_LIB 算法。
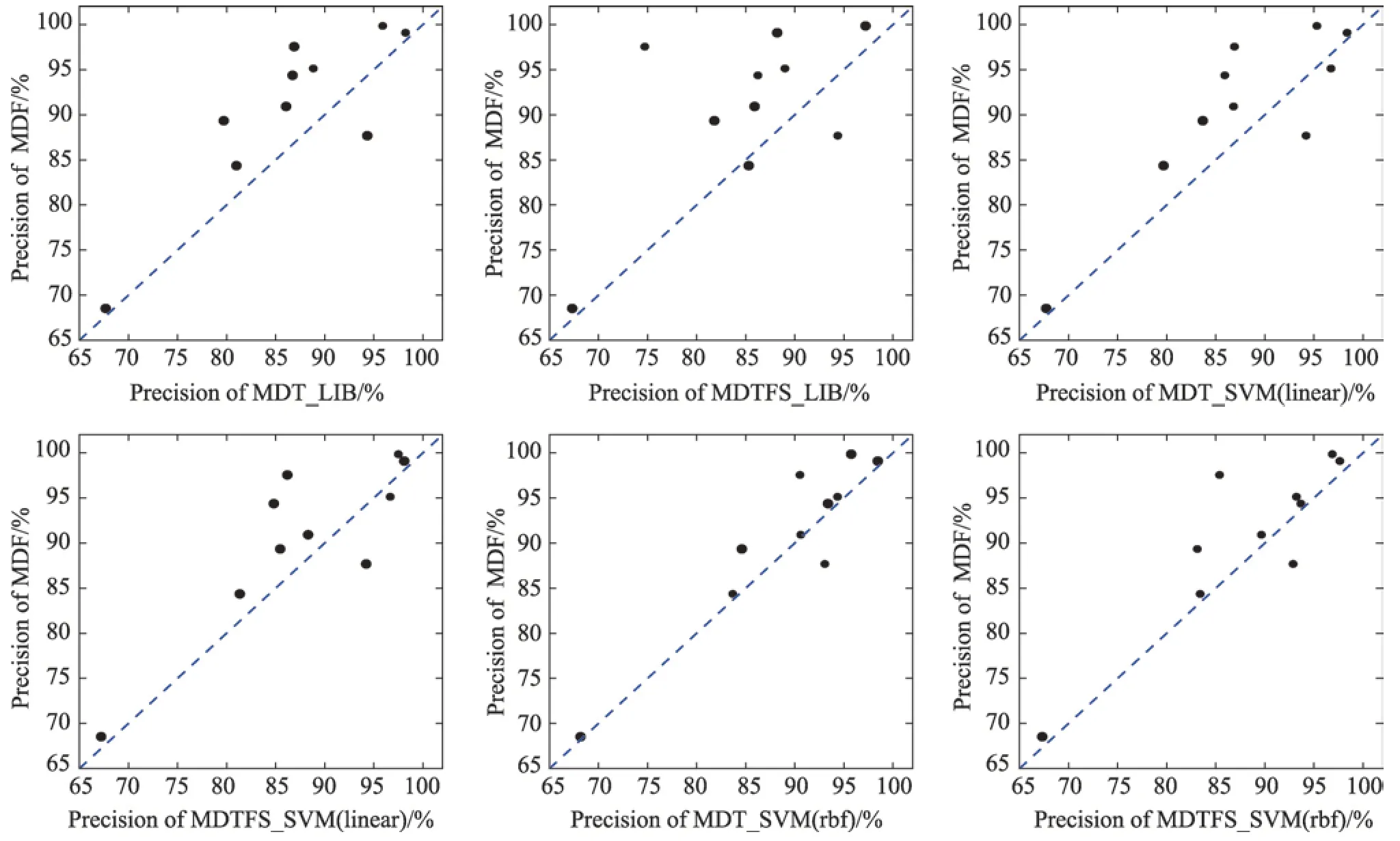
Fig.2 Precision comparison of 7 methods图2 7 种方法精度对比
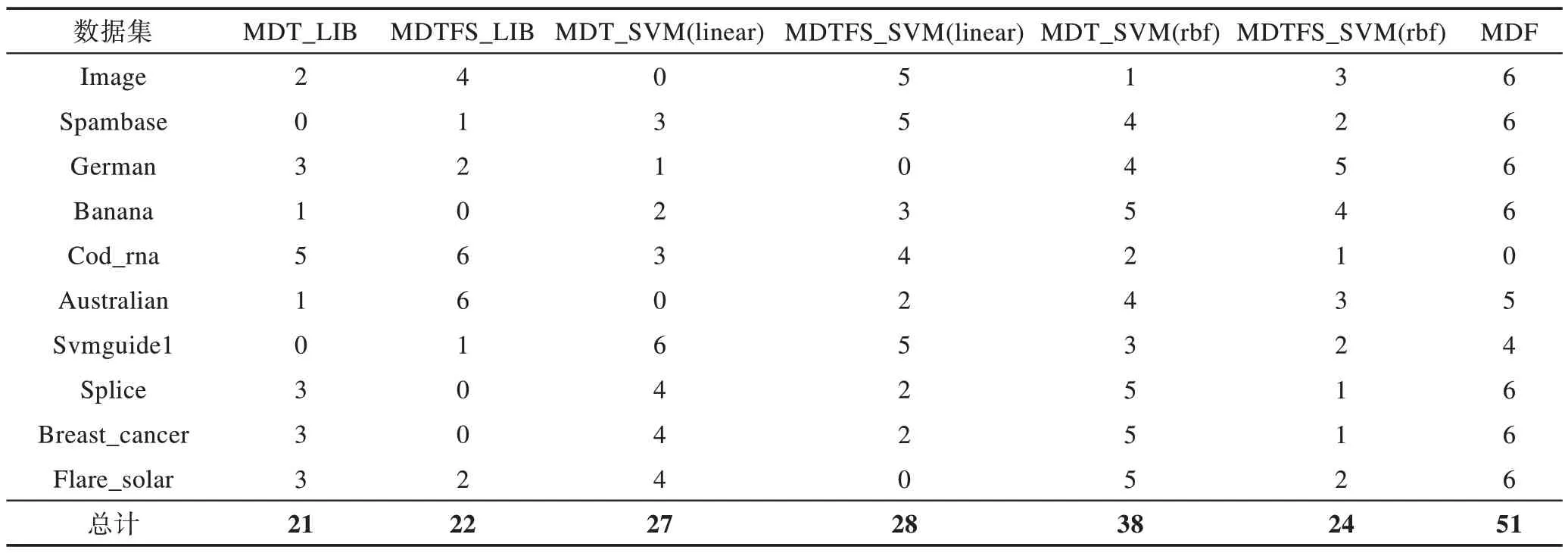
Table 6 Sorting results of 7 methods表6 7 种方法排序结果
综上,MDF 算法的分类性能有一定的优势,尤其是与MDT 算法相比。
(4)与随机森林算法的比较
为了更好地说明本文提出的MDF 算法的性能,将之与随机森林算法的分类错误率进行了比较。实验结果如表7 所示,其中参数L与MDF 相同,即L=10。
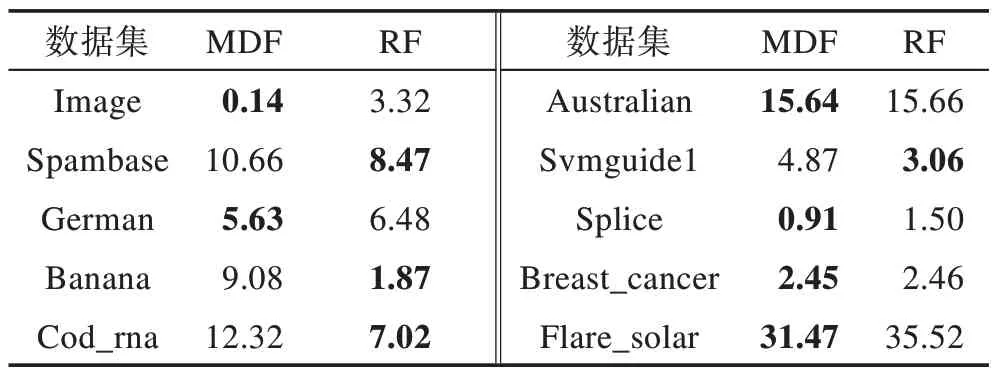
Table 7 Classification error rate of 2 methods表7 两种方法分类错误率 %
根据表7 可以看出,在6 个数据集上MDF 算法的分类错误率比RF 小,在其他4 个数据集上RF 的错误率小于MDF。其中,在Banana 和Cod_rna 两个数据集上RF 的错误率比MDF 小得较多,在image 数据集上MDF 比RF 的错误率小得较多。这说明本文提出的MDF 算法还有进一步提升的空间。
4 结束语
本文提出了一种模型决策森林算法,它将模型决策树作为基分类器,利用随机森林的思想,生成多棵模型决策树。与MDT 相比,MDF 对参数不敏感,因此可以设置较小的参数值从而减少训练时间,同时多棵树集成以后的精度比MDT 高。另外,MDF 在树的数量较少时也能取到不错的精度,避免了因树的数量增加时间复杂度增高的问题。在大数据环境下,如何构建更鲁棒的模型决策森林将是未来的研究重点。
